Partitioning climate projection uncertainty with multiple large ensembles and CMIP5/6

Partitioning uncertainty in projections of future climate change into contributions from internal variability, model response uncertainty and emissions scenarios has historically relied on making assumptions about forced changes in the mean and variability. With the advent of multiple single-model initial-condition large ensembles (SMILEs), these assumptions can be scrutinized, as they allow a more robust separation between sources of uncertainty. Here, the framework from Hawkins and Sutton (2009) for uncertainty partitioning is revisited for temperature and precipitation projections using seven SMILEs and the Coupled Model Intercomparison Project CMIP5 and CMIP6 archives. The original approach is shown to work well at global scales (potential method bias < 20 %), while at local to regional scales such as British Isles temperature or Sahel precipitation, there is a notable potential method bias (up to 50 %), and more accurate partitioning of uncertainty is achieved through the use of SMILEs. Whenever internal variability and forced changes therein are important, the need to evaluate and improve the representation of variability in models is evident. The available SMILEs are shown to be a good representation of the CMIP5 model diversity in many situations, making them a useful tool for interpreting CMIP5. CMIP6 often shows larger absolute and relative model uncertainty than CMIP5, although part of this difference can be reconciled with the higher average transient climate response in CMIP6. This study demonstrates the added value of a collection of SMILEs for quantifying and diagnosing uncertainty in climate projections.

1 Introduction

Climate change projections are uncertain. Characterizing this uncertainty has been helpful not only for scientific interpretation and guiding model development but also for science communication (e.g., Hawkins and Sutton, 2009; Rowell, 2012; Knutti and Sedláček, 2012). With the advent of Coupled Model Intercomparison Projects (CMIPs), a systematic characterization of projection uncertainty became possible, as a number of climate models of similar complexity provided simulations over a consistent time period and with the same set of emissions scenarios. Uncertainties in climate change projections can be attributed to different sources – in context of CMIP to three specific ones (Hawkins and Sutton, 2009), described as follows.

Uncertainty from internal unforced variability: the fact that a projection of climate is uncertain at any given point in the future due to the chaotic and thus unpredictable evolution of the climate system. This uncertainty is inherently irreducible on timescales after which initial condition information has been lost (typically a few years or less for the atmosphere, e.g., Lorenz, 1963, 1996). Internal variability in a climate model can be best estimated from a long control simulation or a large ensemble, including how variability might change under external forcing (Brown et al., 2017; Maher et al., 2018).

Climate response uncertainty (hereafter “model uncertainty”, for consistency with historical terminology): structural differences between models and how they respond to external forcing. Arising from choices made by individual modeling centers during the construction and tuning of their model, this uncertainty is in principle reducible as the differences between models (and between models and observations) are artifacts of model imperfection. In practice, reduction of this uncertainty progresses slowly and might even have limits imposed by the positive feedbacks that determine climate sensitivity (Roe and Baker, 2007). To be able to distinguish model uncertainty from internal variability uncertainty, a robust estimate of a model's “forced response”, i.e., its response to external radiative forcing of a given emissions scenario, is required. Again, a convenient way to obtain a robust estimate of the forced response is to average over a large initial-condition ensemble from a single model (Deser et al., 2012; Frankcombe et al., 2018; Maher et al., 2019).

Radiative forcing uncertainty (hereafter “scenario uncertainty”): lack of knowledge of future radiative forcing that arises primarily from unknown future greenhouse gas emissions. Scenario uncertainty can be quantified by comparing a consistent and sufficiently large set of models run under different emissions scenarios. This uncertainty is considered irreducible from a climate science perspective, as the scenarios are socioeconomic what-if scenarios and do not have any probabilities assigned (which does not imply they are equally likely in reality).

Another important source of uncertainty not explicitly addressable within the CMIP context is parameter uncertainty. Even within a single model structure, some response uncertainty can result from varying model parameters in a perturbed-physics ensemble (Murphy et al., 2004; Sanderson et al., 2008). Such parameter uncertainty is sampled inherently but non-systematically through a set of different models, such as CMIP. Thus, it is currently convoluted with the structural uncertainty as described by model uncertainty, and a proper quantification for CMIP is not possible due to the lack of perturbed-physics ensembles from different models.

In a paper from 2009, Hawkins and Sutton (hereafter HS09) made use of the most comprehensive CMIP archive at the time (CMIP3; Meehl et al., 2007) to perform a separation of uncertainty sources for surface air temperature at global to regional scales. Such a separation helps identify where model uncertainty is large and thus where investments in model development and improvement might be most beneficial (HS09). A robust quantification of projection uncertainty will also benefit multidisciplinary climate change risk assessments, which often rely on quantified likelihoods from physical climate science (King et al., 2015; Sutton, 2019). Due to the lack of large ensembles or even multiple ensemble members from individual models in CMIP3, it was necessary to make an assumption about the forced response of a given model. In HS09, a fourth-order polynomial fit to global and regional temperature time series represented the forced response, while the residual from this fit represented the internal variability. Using 15 models and three emissions scenarios, this enabled a separation of sources of uncertainty in temperature projections, which was later expanded to precipitation (Hawkins and Sutton, 2011; hereafter HS11).

However, the HS09 approach is likely to conflate internal variability with the forced response in cases where there exists low-frequency (decadal-to-multidecadal) internal variability, after large volcanic eruptions or when the forced signal is weak, making the statistical fit a poor estimate of the forced response (Kumar and Ganguly, 2018). HS09 tried to circumvent this issue by focusing on large enough regions and a future without volcanic eruptions, such that there was reason to believe that the spatial averaging would dampen variability sufficiently for it not to alias into the estimate of the forced response described by the statistical fit.

An alternative to statistical fits to estimate the forced response in a single simulation is a single-model initial-condition large ensemble (SMILE). A SMILE enables the robust quantification of a model's forced response and internal variability via computation of ensemble statistics, provided the ensemble size is large enough. Due to their computational costs, SMILEs have not been wide spread even in the latest CMIP6 archive. Nevertheless, since HS09, a number of modeling centers have conducted SMILEs (Selten et al., 2004; Deser et al., 2012, 2020; Kay et al., 2015 and references therein). Thanks to their sample size, SMILEs have been applied most successfully to problems of regional detection and attribution (Deser et al., 2012; Frölicher et al., 2016; Kumar and Ganguly, 2018; Lehner et al., 2017a, 2018; Lovenduski et al., 2016; Mankin and Diffenbaugh, 2015; Marotzke, 2019; Rodgers et al., 2015; Sanderson et al., 2018; Schlunegger et al., 2019), extreme and compound events (Fischer et al., 2014, 2018; Kirchmeier-Young et al., 2017; Schaller et al., 2018), and as test beds for method development (Barnes et al., 2019; Beusch et al., 2020; Frankignoul et al., 2017; Lehner et al., 2017b; McKinnon et al., 2017; Sippel et al., 2019; Wills et al., 2018).

The availability of a collection of SMILEs (Deser et al., 2020) now provides the ability to scrutinize and ultimately drop the assumptions of the original HS09 approach. Further, it allows a separation of the sources of projection uncertainty at smaller scales and for noisier variables. With multiple SMILEs, one can directly quantify the evolving fractional contributions of internal variability and model structural differences to the total projection uncertainty under a given emissions scenario. A SMILE gives a robust estimate of a model's internal variability, and multiple SMILEs thus also enable differentiating robustly between magnitudes of internal variability across models. Recent studies used multiple SMILEs to show that the magnitude of internal variability differs between models to the point that it affects whether internal variability or model uncertainty is the dominant source of uncertainty in near-term projections of temperature (Maher et al., 2020) and ocean biogeochemistry (Schlunegger et al., 2020). Building on that, one can also assess the contribution of any forced change in internal variability by comparing the time-evolving variability across ensemble members with the constant variability from present-day or a control simulation (Pendergrass et al., 2017; Maher et al., 2018; Schlunegger et al., 2020). Here, we revisit the HS09 approach using temperature and precipitation projections from multiple SMILEs, CMIP5 and CMIP6 to illustrate where it works, where it has limitations and how SMILEs can be used to complement the original approach.

2 Data and methods

2.1 Model simulations

We make use of seven publicly available SMILEs that are part of the Multi-Model Large Ensemble Archive (MMLEA; Table 1), centrally archived at the National Center for Atmospheric Research (Deser et al., 2020). All use CMIP5-class models (except MPI, which is closer to its CMIP6 version), although not all of the simulations were part of the CMIP5 submission of the individual modeling centers and were thus not accessible in a centralized fashion until recently. All SMILEs used here were run under the standard CMIP5 “historical” and Representative Concentration Pathway 8.5 (RCP8.5) forcing protocols and are thus directly comparable to corresponding CMIP5 simulations (Taylor et al., 2007). The models range from ∼2.8 to ∼1^∘ horizontal resolution and from 16 to 100 ensemble members. For model evaluation and other applications, the reader is referred to the references in Table 1. We also use all CMIP5 models for which simulations under RCP2.6, RCP4.5 and RCP8.5 are available (28; Table S1 in the Supplement) and all CMIP6 models for which simulations under SSP1-2.6, SSP2-4.5, SSP3-7.0 and SSP5-8.5 are available (21, as of November 2019; Table S1; Eyring et al., 2016; O'Neill et al., 2016). A single ensemble member per model is used from the CMIP5 and CMIP6 archives at ETH Zürich (Brunner et al., 2020b). All simulations are regridded conservatively to a regular 2.5^∘ × 2.5^∘ grid.

Table 1 Single-model initial-condition large ensembles (SMILEs) used in this study. Table reproduced from Deser et al. (2020). See also http://www.cesm.ucar.edu/projects/community-projects/MMLEA/ (last access: 27 May 2020).

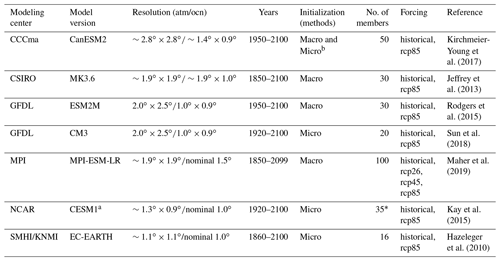
^a CESM1: only the first 35 members of 40 available are used, since members 36–40 are slightly warmer erroneously (see http://www.cesm.ucar.edu/projects/community-projects/LENS/known-issues.html, last access: 27 May 2020), which can affect the variability estimates when calculated across the ensemble. ^b Stainforth et al. (2007) and Hawkins et al. (2026).

2.2 Uncertainty partitioning

We partition three sources of uncertainty largely following HS09, such that the total uncertainty (T) is the sum of the model uncertainty (M), the internal variability uncertainty (I) and the scenario uncertainty (S), each of which can be estimated as variance for a given time t and location l as follows:

$$\begin{array}{}\text{(1)}& T(t,l)=M(t,l)+I(t,l)+S(t,l),\end{array}$$

with the fractional uncertainty from a given source calculated as $\frac{M(t,l)}{T(t,l)}$, $\frac{I(t,l)}{T(t,l)}$ and $\frac{S(t,l)}{T(t,l)}$. This formulation assumes the sources of uncertainty are additive, which strictly speaking is not valid due the terms not being orthogonal (e.g., model and scenario uncertainty). In practice, an ANOVA formulation with interaction terms yields similar results and conclusions (Yip et al., 2011).

There are different ways to define M, I and S, in part depending on the information obtainable from the available model simulations (e.g., SMILEs versus CMIP). For the SMILEs, the model uncertainty M is calculated as the variance across the ensemble means of the seven SMILEs (i.e., across the forced responses of the SMILEs). The internal variability uncertainty I is calculated as the variance across ensemble members of a given SMILE, yielding one estimate of I per model. Prior to this calculation, time series are smoothed with the running mean corresponding to the target metric (here mostly decadal means). Averaging across the seven I values yields the multimodel mean internal variability uncertainty I_mean. Alternatively, to explore the assumption that I_mean does not change over time, we use the 1950–2014 average value of I_mean throughout the calculation (i.e., I_fixed). We also use the model with the largest and smallest I, i.e., I_max and I_min, to quantify the influence of model uncertainty in the estimate of I.

The uncertainties M and I for CMIP, in turn, are calculated as in HS09: the forced response is estimated as a fourth-order polynomial fit to the first ensemble member of each model. The model uncertainty M is then calculated as the variance across the estimated forced responses. To be comparable with the SMILE calculations, only simulations from RCP8.5 and SSP5-8.5 are used for the calculation of M in CMIP; this neglects the fact that, for the same set of models, model uncertainty is typically slightly smaller in weaker emissions scenarios. The internal variability uncertainty I is defined as the variance over time from 1950 to 2099 of the residual from the forced response of a given model. Prior to this calculation, time series are smoothed with the running mean corresponding to the target metric. Historical volcanic eruptions can thus affect I in CMIP, while for SMILEs I is more independent of volcanic eruptions since it is calculated across ensemble members. In practice, this difference was found to be very small (Sect. S1 in the Supplement). Averaging across all I values in CMIP yields the multimodel mean internal variability uncertainty I_mean, which, unlike the SMILE-based I_mean, is time-invariant. We also apply the HS09 approach to each ensemble member of each SMILE to explore the impact of the method choice.

Estimating the scenario uncertainty S relies on the availability of an equal set of models that were run under divergent emissions scenarios. Since only few of the SMILEs were run with more than one emissions scenario, we turn to CMIP5 for the scenario uncertainty. Following HS09, we calculate S as the variance across the multimodel means calculated for the different emissions scenarios, using a consistent set of available models. We use the CMIP5-derived S in all calculations related to SMILEs. There are alternative ways to calculate S that are briefly explored here but not used in the remainder of the paper (see Sect. S2): (1) use the scenario uncertainty from a SMILE that provides ensembles for different scenarios (e.g., MPI-ESM-LR or CanESM5). The benefit would be a robust estimate of scenario uncertainty (since the forced response is well known for each scenario), while the downside would be that a single SMILE is not representative of the scenario uncertainty as determined from multiple models (Fig. S2). (2) Calculate scenario uncertainty first for each model by taking the variance across the scenarios of a given model, and then average all of these values to obtain S (Brekke and Barsugli, 2013). The benefit would be a better quantification of scenario uncertainty in case of a small multimodel mean signal with ambiguous sign (Fig. S3).

In addition to the fractional uncertainties, the total uncertainty of a multimodel multi-scenario mean projection is also calculated following HS09: 90 % uncertainty ranges are calculated additively and symmetrically around the multimodel multi-scenario mean as $\pm \frac{\mathrm{1.654}\cdot \sqrt{I}}{F}$, $\pm \frac{\mathrm{1.654}\cdot (\sqrt{I}+\sqrt{M})}{F}$ and $\pm \frac{\mathrm{1.654}\cdot (\sqrt{I}+\sqrt{M}+\sqrt{S})}{F}$, with $F=\frac{\sqrt{I}+\sqrt{M}+\sqrt{S}}{\sqrt{I+M+S}}$. Note that the assumption of symmetry is an approximation, which is violated already by the skewed distribution of available emissions scenarios (e.g., 2.6, 4.5 and 8.5 W m⁻² in CMIP5) and possibly also by the distribution of models, which constitute an ensemble of opportunity rather than a particular statistical distribution (Tebaldi and Knutti, 2007). Thus, the figures corresponding to this particular calculation should only be regarded as an illustration rather than a quantitative depiction of the multimodel multi-scenario uncertainty. Also, the original depiction in HS09 was criticized for giving the impression of a “best-estimate” projection resulting from averaging the responses across all scenarios. That impression is false since the scenarios are not assigned any probabilities; thus their average is not more likely to occur than any individual scenario. To avoid giving this false impression, here we rearrange the depiction of absolute uncertainty as compared to HS09 and HS11.

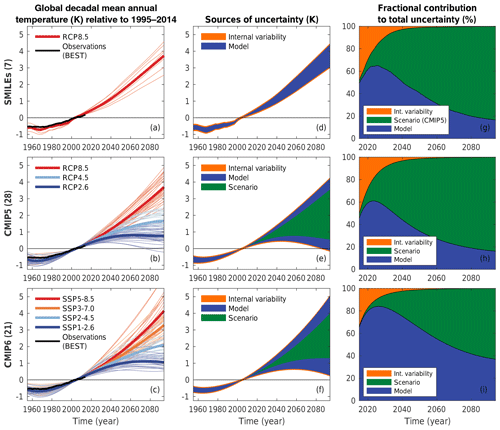
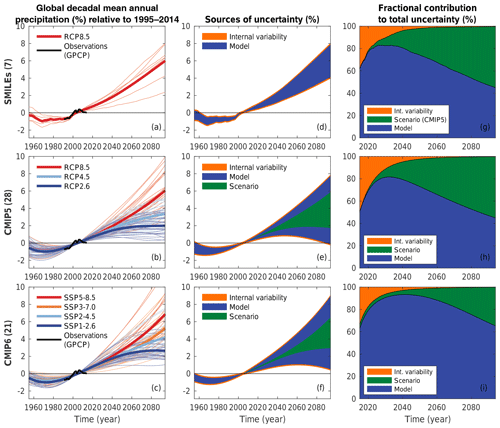
Figure 1 (a–c) 10-year running means of global annual mean temperature time series from (a) SMILEs, (b) CMIP5 and (c) CMIP6, with observations (Rohde et al., 2013) superimposed in black, all relative to 1995–2014. For SMILEs, the ensemble mean of each model and the multimodel average of those ensemble means are shown; for CMIP the polynomial fit for each model and the multimodel average of those fits are shown. (d–f) Illustration of the sources of uncertainty in the multimodel multi-scenario mean projection. (g–i) Fractional contribution of individual sources to total uncertainty. Scenario uncertainty in SMILEs in (g) is taken from CMIP5, since not all SMILEs offer simulations with multiple scenarios. (d–i) In all cases, the respective multimodel mean estimate of internal variability (I_mean) is used.

3 Results

3.1 Global mean temperature and precipitation projection uncertainty

We first consider global area-averaged temperature and precipitation projections and their uncertainties (Figs. 1 and 2). Under RCP8.5 and SSP5-8.5, decadal global mean annual temperature is projected to increase robustly in the SMILEs and CMIP5/6 (Fig. 1a–c). Other scenarios result in less warming, as expected. These projections are then broken into the different sources of uncertainties (Fig. 1d–f). Finally, the different uncertainties are expressed as time-evolving fraction of the total uncertainty (Fig. 1g–i). Note that Fig. 1d–f and g–i essentially show absolute and relative uncertainties. Thus, Fig. 1d–f are most useful to answer the question “how large is the uncertainty of a projection for year X and what sources contribute how much?”, while Fig. 1g–i are most useful to answer the question “which sources are most important to the projection uncertainty from now to year X?”. This nuance is easily appreciated when thinking about internal variability uncertainty, which remains roughly constant in an absolute sense but approaches zero in a relative sense for longer lead times.

Figure 2 As Fig. 1 but for precipitation (observations from Adler et al., 2003).

The projection uncertainty in decadal global mean temperature shows a breakdown familiar from HS09: internal variability uncertainty is important initially, followed by model uncertainty increasing and eventually dominating the first half of the 21st century, before scenario uncertainty becomes dominant by about mid-century (Fig. 1g–i). SMILEs and CMIP5 behave very similarly, attesting that the seven SMILE models are a good representation of the 28 CMIP5 models for global mean temperature projections. This holds for other variables and large-scale regions subsequently investigated (Fig. S4), which is also consistent with the coincidental structural independence between the seven SMILEs (Knutti et al., 2013; Sanderson et al., 2015b). CMIP6, in turn, shows a larger model uncertainty, both in an absolute (Fig. 1f) and relative (Fig. 1i) sense. Since the scenario uncertainty in CMIP6 is by design similar to CMIP5 (spanning radiative forcings from 2.6 to 8.5 W m⁻²), this result is indeed attributable to larger model uncertainty – consistent with the wider range of climate sensitivities and transient responses reported for CMIP6 compared to CMIP5 (Tokarska et al., 2020), a point we will return to in Sect. 3.5. The lack of high-sensitivity models in CMIP5 compared to CMIP6 results in the 90 % uncertainty range intersecting with zero in CMIP5 (Fig. 1e) but not CMIP6 (Fig. 1f). Absolute internal variability is slightly smaller in CMIP6 (Fig. 1f) compared to CMIP5 but not significantly so, and therefore this factor is not responsible for the relatively smaller contribution to total uncertainty from internal variability in CMIP6 (Fig. 1i).

Projections of global mean precipitation largely follow the breakdown found for temperature (Fig. 2). Again, SMILEs and CMIP5 behave remarkably similarly, while CMIP6 shows larger model uncertainty compared to CMIP5; model uncertainty dominates CMIP6 throughout the 21st century, still contributing >60 % by the last decade (compared to ∼45 % in SMILEs and CMIP5).

3.2 Spatial patterns of temperature and precipitation projection uncertainty

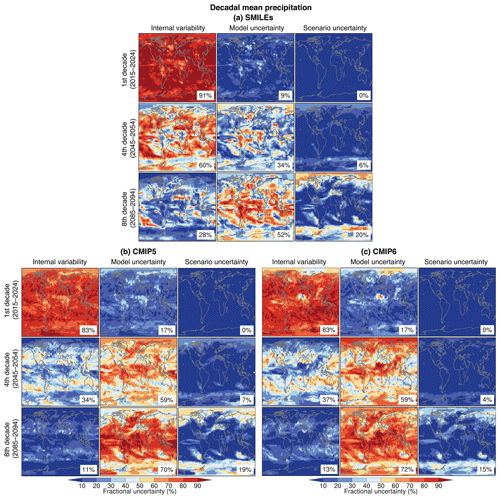
We recreate the maps from Fig. 6 in HS09 for decadal mean temperature, showing the spatial patterns of different sources of uncertainty for lead times of 1, 4 and 8 decades, relative to the reference period 1995–2014 (Fig. 3). The patterns of fractional uncertainty contributions generally look similar for SMILEs and CMIP5/6 (and also similar to CMIP3 in HS09; not shown). In the first decade, internal variability contributes least in the tropics and most in the high latitudes. By the fourth decade, internal variability contributes least almost everywhere. Scenario uncertainty increases earliest in the tropics, where signal to noise is known to be large for temperature (HS09; Mahlstein et al., 2011; Hawkins et al., 2020). By the eighth decade, scenario uncertainty dominates everywhere except over the subpolar North Atlantic and the Southern Ocean, owing to the documented model uncertainty in the magnitude of ocean heat uptake as a result of forced ocean circulation changes (Frölicher et al., 2015). While the patterns are largely consistent between the model generations (see also Maher et al., 2020), there are differences in magnitude. As noted in Sect. 3.1, CMIP6 has a larger model uncertainty than CMIP5 (global averages of model uncertainty for the different lead times in CMIP6: 40 %, 65 % and 45 %; in CMIP5: 14 %, 26 % and 24 %). CMIP6 also has a longer consistent forcing period than CMIP5, as historical forcing ends in 2005 in CMIP5 and 2014 in CMIP6. These two factors lead to the fractional contribution from scenario uncertainty being smaller in CMIP6 compared to CMIP5 and SMILEs throughout the century (global averages of scenario uncertainty for different lead times in CMIP6: 2 %, 26 % and 54 %; in CMIP5: 31 %, 65 % and 74 %). Thus, the forcing trajectory and reference period need to be considered when interpreting uncertainty partitioning and when comparing model generations. An easy solution would be to ignore scenario uncertainty or normalize projections in another way (see Sect. 3.5).

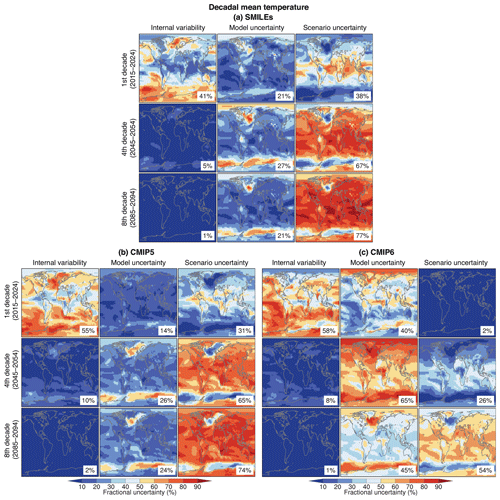
Figure 3 Fraction of variance explained by the three sources of uncertainty in projections of decadal mean temperature changes in 2015–2024, 2045–2054 and 2085–2094 relative to 1995–2014, from (a) SMILEs, (b) CMIP5 models and (c) CMIP6 models. Percentage numbers give the area-weighted global average value for each map.

Figure 4 As in Fig. 3 but for precipitation.

The spatial patterns for precipitation generally also look similar between SMILEs and CMIP5/6 (and CMIP3 in HS11; Fig. 4; not shown). Internal variability dominates worldwide in the first decade and remains important during the fourth decade, in particular in the extratropics, while the tropics start to be dominated by model uncertainty. The North Atlantic and Arctic also start to be dominated by model uncertainty by the fourth decade. Scenario uncertainty remains unimportant throughout the century in most places. While there is agreement on the patterns, there are notable differences between the SMILEs and CMIP5/6 with regard to the magnitude of a given uncertainty source: substantially more uncertainty gets partitioned towards model uncertainty in CMIP compared to SMILEs (global averages for model uncertainty in first and fourth decade in CMIP5/6: 17 %∕17 % and 59 %∕59 %; in SMILEs: 9 % and 34 %) despite the good agreement between the global multimodel mean precipitation projections from SMILEs and CMIP (Fig. 2). Consequently, internal variability appears less important in CMIP than in SMILEs. This result is consistent with the expectation that, at small spatial scales (here 2.5^∘ × 2.5 ^∘), the HS09 polynomial fit tends to wrongly interpret internal variability as part of the forced response, thus artificially inflating model uncertainty. We quantify this “bias” through the use of SMILEs in the next section.

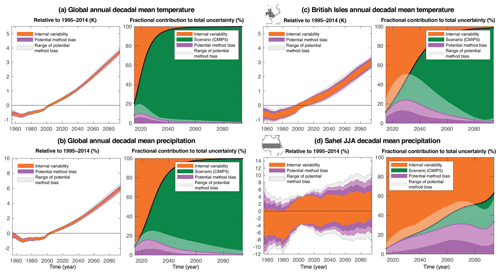
Figure 5 Decadal mean projections from SMILEs and fractional contribution to total uncertainty (using scenario uncertainty from CMIP5) for (a) global mean annual temperature, (b) global mean annual precipitation, (c) British Isles annual temperature and (d) Sahel June–August precipitation. The pink color indicates the potential method bias and is calculated the same way as model uncertainty in the HS09 approach, except instead of different models we only use different ensemble members from a SMILE; thus if the HS09 method were perfect, the bias would be zero. This potential method bias is calculated using each SMILE in turn, and then the mean value from the seven SMILEs is used for the dark pink curve, while the slightly transparent white shading around the pink curve is the range of the potential method bias based on different SMILEs.

3.3 Role of choice of method to estimate the forced response

One of the caveats of the HS09 approach is the necessity to estimate the forced response via a statistical fit to each model simulation rather than using the ensemble mean of a large ensemble. Here, we quantify the potential bias that stems from using a fourth-order polynomial to estimate the forced response in a perfect model setup. Specifically, we use one SMILE and treat each of its ensemble members as if it were a different model, applying the polynomial fit to estimate each ensemble member's forced response. By design, model uncertainty calculated from these forced response estimates should be zero (since they are all from a single model), and any deviation from zero will indicate the magnitude of the method bias. We calculate this potential method bias using each SMILE in turn.

For global temperature, this bias is small but clearly nonzero and peaks around year 2020 at a contribution of about 10 % to the total uncertainty (comprised of potential method bias, internal variability and scenario uncertainty) and a range from 8 % to 20 % depending on which SMILE is used in the perfect model setup (Fig. 5a). The bias decreases to <5 % by 2040. For global precipitation, the bias is larger, peaking at about 25 % in the 2020s and taking until 2100 to reduce to <5 % in all SMILEs (Fig. 5b). These potential biases are visible even in global mean quantities, where the spatial averaging should help in estimating the forced response from a single member. Consequently, potential biases are even larger at regional scales. For example, and to revisit some cases from HS09 and HS11, for decadal temperature averaged over the British Isles, the bias contribution can range between 10 % and 50 % at its largest (Fig. 5c). For decadal monsoonal precipitation over the Sahel, the method bias is also large and – due to the small scenario uncertainty and gradually diminishing internal variability contribution over time – contributes to the total uncertainty throughout the entire century (Fig. 5d).

The potential method bias from using a polynomial fit has a spatial pattern, too (Fig. 6). For temperature, it is largest in the extratropics and smallest in the tropics (Fig. 6a). In regions of deep water formation, where the forced trend is small and an accurate estimate of it is thus difficult, the potential bias contribution to the total uncertainty can be >50 % even in the fourth decade. For precipitation, the potential method bias is almost uniform across the globe and remains sizable throughout the century (Fig. 6b), consistent with the Sahel example in Fig. 5d. By the eighth decade, the contribution from potential method bias starts to decrease and does so first in regions with a clear forced response (subtropical dry zones getting drier and high latitudes getting wetter), as there, scenario uncertainty ends up dominating the other uncertainty sources.

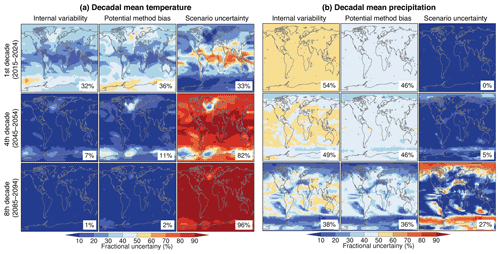
Figure 6 Fraction of variance explained by internal variability, potential method bias and scenario uncertainty in projections of decadal mean changes in 2015–2024, 2045–2054 and 2085–2094 relative to 1995–2014, for (a) temperature and (b) precipitation. The potential method bias is calculated the same way as model uncertainty in the HS09 approach, except instead of different models we only use different ensemble members from one SMILE; thus if the HS09 method were perfect, the bias would be zero. The potential method bias is calculated using each SMILE in turn, and then the mean value from the seven SMILEs is used for the maps here. Percentage numbers give the area-weighted global average value for each map.

The potential method bias portrayed here can largely be reduced using SMILEs, at least if the ensemble size of a SMILE is large enough to robustly estimate the forced response (Coats and Mankin, 2016; Milinski et al., 2019). To test for ensemble size sufficiency, we calculate the potential method bias as the variance of 100 different ensemble means, each calculated by subsampling the largest SMILE (MPI; n=100) at the size of the smallest SMILE (EC-EARTH; n=16). We find the potential method bias from an ensemble mean of 16 members to be substantially smaller than with the HS09 approach (Fig. S5).

If there are such large potential biases in estimating model uncertainty and internal variability, why are the results for SMILEs and CMIP5 overall still so similar (see Figs. 1 and 2)? Despite the imperfect separation of internal variability and forced response in HS09, the central estimate of variance across models is affected less if a large enough number of models is used (here, 28 from CMIP5). A sufficient number of models can partly compensate for the biased estimate of the forced response in any given model and – consistent with the central limit theorem – overall still results in a robust estimate of model uncertainty. The number of models needed varies with the question at hand and is larger for smaller spatial scales. For example, the potential method bias for British Isles temperature appears to be too large to be overcome completely by the CMIP5 sample size, resulting in a biased uncertainty partitioning there (see also Sect. 3.5). HS09 used 15 CMIP3 models and large spatial scales to circumvent much of this issue, although it is important to remember that the potential bias in estimating the variance in a population increases exponentially with decreasing sample size. In the special case of climate models, which can be interdependent (Abramowitz et al., 2019; Knutti et al., 2013; Masson and Knutti, 2011), the potential bias might grow slower or faster than that.

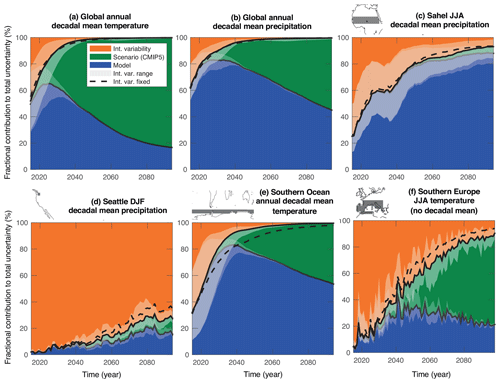
Figure 7 Sources of uncertainty from SMILEs (using scenario uncertainty from CMIP5) for different regions, seasons and variables. The solid black lines indicate the borders between sources of uncertainty; the slightly transparent white shading around those lines is the range of this estimate based on different SMILEs. The dashed line marks the dividing line if internal variability is assumed to stay fixed at its 1950–2014 multi-SMILE mean. All panels are for decadal mean projections, except (f) southern Europe June–August temperature, to which no decadal mean has been applied.

3.4 Role of model uncertainty in and forced changes of internal variability

Model uncertainty in internal variability itself can have an effect on some climate indices (Deser et al., 2020; Maher et al., 2020; Schlunegger et al., 2020). The fraction of global temperature projection uncertainty attributable to internal variability varies by almost 50 percentage points around I_mean at the beginning of the century, depending on whether I_max or I_min is used from the pool of SMILEs (range of white shading in Fig. 7a). This fraction diminishes rapidly with time as importance of internal variability generally decreases, but model differences in internal variability remain important over the next few decades (consistent with Maher et al., 2020, and Schlunegger et al., 2020). Global precipitation behaves similarly to temperature, except the range of internal variability contributions from the different SMILEs is relatively smaller (Fig. 7b). Another example of uncertainty in internal variability itself is the magnitude of decadal variability of summer monsoon precipitation in the Sahel, which varies considerably across the SMILEs, resulting in internal variability contributing anywhere between about 40 % and 80 % in the first half of the century (range of white shading in Fig. 7c). The wide spread in the magnitude of variability across models suggests that at least some models are biased in their variability magnitude. Understanding and resolving biases in variability in fully coupled models is important for attribution of observed variability as well as for efforts of decadal prediction. Sahel precipitation, for example, has a strong relationship with the Atlantic Ocean's decadal variability, which is one of few predictable climate indices globally (Yeager et al., 2018). In the case such decadal variability originates from an underlying oscillation, the SMILE-sampling of different oscillation phases contributes to ensemble spread and also complicates the evaluation of simulated internal variability with short observational records. Similar issues have been documented for the Indian monsoon (Kodra et al., 2012). Thus, a realistic representation of variability together with initialization on the correct phase of potential oscillations are prerequisites for skillful decadal predictions.

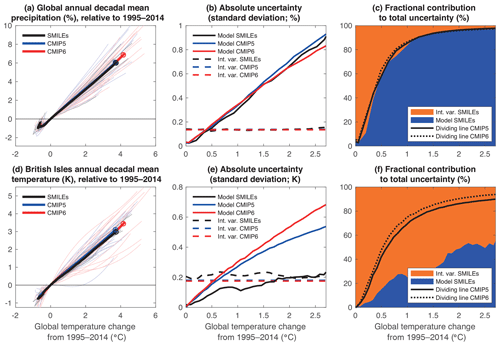
Figure 8 (a) Decadal means of global mean precipitation change as a function of global mean temperature change. Thin lines are forced response estimates from individual models, and thick lines are multimodel means for SMILEs, CMIP5 and CMIP6. The last decade of each multimodel mean is marked with a circle. (b) Uncertainty in global mean precipitation changes from model differences and internal variability in SMILEs, CMIP5 and CMIP6 as a function of global mean temperature. (c) Fractional contribution of global mean precipitation changes from model uncertainty and internal variability to total uncertainty as a function of global mean temperature. The colors indicate the fractional uncertainties from internal variability and model uncertainty in SMILEs, while the solid and dotted lines indicate where the dividing line between these two sources of uncertainty (i.e., between orange and blue colors) would lie for CMIP5 and CMIP6. (d–f) Same as (a)–(c) but for British Isles temperature.

Internal variability can change in response to forcing, which can be assessed more robustly through the use of SMILEs. Comparing I_fixed (which assumes no such change) with I_mean shows that there is no clear forced change in decadal global annual temperature variability over time (Fig. 7a). Forced changes to precipitation variability are expected in many locations (Knutti and Sedláček, 2012; Pendergrass et al., 2017), although robust quantification – in particular for decadal variability – has previously been hampered by the lack of large ensembles. Here, we show that forced changes in variability can now be detected for noisy time series and small spatial scales, such as winter precipitation near Seattle, USA (Fig. 7d). Note, however, that in this example the increase in variability is small relative to the large internal variability, which is responsible for over 70 % of projection uncertainty even at the end of the century. Forced changes in temperature variability are typically less wide spread and less robust than those in precipitation but can be detected in decadal temperature variability in some regions, for example the Southern Ocean (Fig. 7e). The projected decrease in temperature variability there could be related to diminished sea ice cover in the future, akin to the Northern Hemisphere high-latitude cryosphere signal (Brown et al., 2017; Holmes et al., 2016; Screen, 2014), and around mid-century reduces the uncertainty contribution from internal variability by more than half compared to the case with fixed internal variability. Another example is the projected increase in summer temperature variability over parts of Europe (Fig. 7f; note that we have not applied the 10-year running mean to this example in order to highlight interannual variability), which is understood to arise from a future strengthening of land–atmosphere coupling (Borodina et al., 2017; Fischer et al., 2012; Seneviratne et al., 2006). All SMILEs agree on the sign of change in internal variability for the cases discussed here.

3.5 Uncertainties normalized by climate sensitivity

One of the emerging properties of the CMIP6 archive is the presence of models with higher climate sensitivity than in CMIP5 (Tokarska et al., 2020; Zelinka et al., 2020). As seen in Figs. 1 and 2, this can result in larger absolute and relative model uncertainty in CMIP6 compared to SMILEs and CMIP5. However, it could be that this is merely a result of the higher climate sensitivity and stronger transient response rather than indicative of increased uncertainty with regard to processes controlled by (global) temperature. To understand whether this is the case, we express sources of uncertainties as a function of global mean temperature (Fig. 8). For example, global mean precipitation scales approximately linearly with global mean temperature under greenhouse gas forcing (Fig. 8a). Indeed, the absolute uncertainties from model differences and internal variability are entirely consistent across SMILEs, CMIP5 and CMIP6 when normalized by global mean temperature (Fig. 8b and c). Thus, uncertainty in global mean precipitation projections remains almost identical between the different model generations, despite the seemingly larger uncertainty depicted in Fig. 2 for CMIP6. A counterexample is projected temperature over the British Isles, where model uncertainty remains slightly larger in CMIP6 than in CMIP5 even when normalized by global mean temperature (Fig. 8d–f). This example also illustrates once again the challenge of correctly estimating the forced response from a single simulation, as the HS09 approach erroneously partitions a significantly larger fraction of total uncertainty into model uncertainty compared to the SMILEs (Fig. 8b and c; see also Fig. 5b).

Alternatively, models can be weighted or constrained according to performance metrics that are physically connected to their future warming magnitude (Hall et al., 2019). The original HS09 paper proposed using the global mean temperature trend over recent decades as an emergent constraint to determine if a model warms too much or too little in response to greenhouse gas forcing. This emergent constraint is relatively simple, and more comprehensive ones have since been proposed (Steinacher and Joos, 2016). However, the original idea has recently found renewed application to overcome the challenge of estimating the cooling magnitude from anthropogenic aerosols over the historical record (Jiménez-de-la-Cuesta and Mauritsen, 2019; Tokarska et al., 2020). Despite regional variations, the aerosol forcing has been approximately constant globally after the 1970s, such that the global temperature trend since then is more likely to resemble the response to other anthropogenic forcings, chiefly greenhouse gases (GHGs), which have steadily increased over the same time. Thus, this period can be used as an observational constraint on the model sensitivity to GHGs. The correlation between the recent warming trend (1981–2014) and the longer trend projected for this century (1981–2100; using RCP8.5 and SSP5-8.5) is significant in CMIP5 (r=0.53) and CMIP6 (r=0.79), suggesting the existence of a meaningful relationship (Tokarska et al., 2020). Following HS09, a weight w_m can be calculated for each model m as follows:

$$\begin{array}{}\text{(2)}& w_{\mathrm{m}}={\displaystyle \frac{\mathrm{1}}{x_{\mathrm{obs}}+\left|x_{\mathrm{m}}-x_{\mathrm{obs}}\right|}},\end{array}$$

with x_obs and x_m being the observed and model-simulated global mean temperature trend from 1981 to 2014. We apply the weighting to CMIP5 and CMIP6 but only to the data used to calculate model uncertainty – scenario uncertainty and internal variability remain unchanged for clarity. The weighting results in an initial reduction of absolute and relative model uncertainty in global mean temperature projections (Fig. 9). The reduction is larger for CMIP6 than for CMIP5, consistent with recent studies suggesting that CMIP6 models overestimate the response to GHGs (Tokarska et al., 2020). Consequently, the weighting brings CMIP5 and CMIP6 global temperature projections into closer agreement, although remaining differences and questions, such as how aggressively to weigh models or how to deal with model interdependence (Knutti et al., 2017), are still to be understood.

Figure 9 (a) Sources of uncertainty in the multimodel multi-scenario mean projection of global annual decadal mean temperature in CMIP5. (b) Fractional contribution of individual sources to total uncertainty. Observationally constrained projections are given by the dotted lines (see text for details). (c, d) Same as (a) and (b) but for CMIP6.

4 Discussion and conclusions

We have assessed the projection uncertainty partitioning approach of Hawkins and Sutton (2009; HS09), in which a fourth-order polynomial fit was used to estimate the forced response from a single-model simulation. We made use of single-model initial-condition large ensembles (SMILEs) with seven different climate models (from the MMLEA) as well as the CMIP5/6 archives. The SMILEs facilitate a more robust separation of forced response and internal variability and thus provide an ideal test bed to benchmark the HS09 approach. We confirm that for averages over large spatial scales (such as global temperature and precipitation), the original HS09 approach provides a reasonably good estimate of the uncertainty partitioning, with potential method biases generally contributing less than 20 % to the total uncertainty. However, for local scales and noisy targets (such as regional or grid-cell averages), the original approach can erroneously attribute internal variability to model uncertainty, with potential method biases at times reaching 50 %. It is worth noting that a large number of models can partly compensate for this method bias. Still, a key result of this study is the need for a robust estimate of the forced response. There are different ways to achieve this – utilizing the MMLEA as done here is one of them. Alternatively, techniques to quantify and remove unforced variability from single simulations, such as dynamical adjustment or signal-to-noise maximization can be used (Allen and Tett, 1999; Deser et al., 2016; Hasselmann, 1979; Sippel et al., 2019; Smoliak et al., 2015; Wallace et al., 2012) and should provide an improvement over a polynomial fit.

Along with a better estimate of the forced response, SMILEs also enable estimating forced changes in variability if a sufficiently large ensemble is available (Milinski et al., 2019). While this study focused mainly on decadal means and thus decadal variability – showing wide-spread increases in precipitation variability and high-latitude decreases in temperature variability –, changes in variability can be assessed at all timescales (Mearns et al., 1997; Pendergrass et al., 2017; Maher et al., 2018; Deser et al., 2020; Milinski et al., 2019; Schlunegger et al., 2020). Whether variability changes matter for impacts needs to be assessed on a case-by-case basis. For example, changes in daily temperature variability can have a disproportionate effect on the tails and thus extreme events (Samset et al., 2019). However, there is a clear need to better validate model internal variability, as we found models to differ considerably in their magnitude of internal variability (consistent with Maher et al., 2020, and Schlunegger et al., 2020), a topic that has so far received less attention (Deser et al., 2018; Simpson et al., 2018). SMILEs, in combination with observational large ensembles (McKinnon et al., 2017; McKinnon and Deser, 2018), are opening the door for that.

SMILEs are still not widespread, running the risk of being nonrepresentative of the “true” model diversity (see Abramowitz et al., 2019, for a review). Thus, to make inferences from SMILEs about the entire CMIP archive, it is necessary to test the representativeness of SMILEs. Fortunately, the seven SMILEs used here are found to be reasonably representative for several targets investigated, but a more systematic comparison is necessary before generalizing this conclusion. For example, while the seven SMILEs used here cover the range of global aerosol forcing estimates in CMIP5 reasonably well (Forster et al., 2013; Rotstayn et al., 2015), their representativeness for questions of regional aerosol forcing remains to be investigated. In any case, further additions to the MMLEA will continue to increase the utility of that resource (Deser et al., 2020).

Finally, we found that the seemingly larger absolute and relative model uncertainty in CMIP6 compared to CMIP5 can to some extent be reconciled by either normalizing projections by global mean temperature or by applying a simple model weighting scheme that targets the emerging high climate sensitivities in CMIP6, consistent with other studies (Jiménez-de-la-Cuesta and Mauritsen, 2019; Tokarska et al., 2020). Constraining the model uncertainty in this way brings CMIP5 and CMIP6 into closer agreement, although differences remain that need to be understood. More generally, continued efforts are needed to include physical constraints when characterizing projection uncertainty, with the goal of striking the right balance between rewarding model skill, honoring model consensus and guarding against model interdependence (Giorgi and Mearns, 2002; O'Gorman and Schneider, 2009; Sanderson et al., 2015a; Smith et al., 2009). Global, regional and multivariate weighting schemes show promise in aiding this effort (Brunner et al., 2019, 2020a; Knutti et al., 2017; Lorenz et al., 2018). Improving the reliability of projections will thus remain a focal point of climate research and climate change risk assessments, with methods for robust uncertainty partitioning being an essential part of that effort.