Cross-scale causal information flow from the El Niño–Southern Oscillation to precipitation in eastern China

The El Niño–Southern Oscillation (ENSO) is a dominant mode of climate variability influencing temperature and precipitation in distant parts of the world. Traditionally, the ENSO influence is assessed considering its amplitude. Focusing on its quasi-oscillatory dynamics comprising multiple timescales, we analyze the causal influence of phases of ENSO oscillatory components on scales of precipitation variability in eastern China, using information-theoretic generalization of Granger causality. We uncover the causal influence of the ENSO quasi-biennial component on the precipitation variability on and around the annual scale, while the amplitude of the precipitation quasi-biennial component is influenced by the low-frequency ENSO components with periods of around 6 years. This cross-scale causal information flow is important mainly in the Yellow River basin (YWRB), while in the Yangtze River basin (YZRB) the causal effect of the ENSO amplitude is dominant. The presented results suggest that, in different regions, different aspects of ENSO dynamics should be employed for prediction of precipitation.

1 Introduction

The Asian summer monsoon (ASM) is the most active monsoon system on the planet, bringing ample moisture from the tropical ocean to the continent and accounting for more than half of yearly rainfall (Krishnamurti, 1971; Wang and LinHo, 2002). The ASM is divided into two major sub-systems: the South Asian summer monsoon (SASM), which is characterized by a pronounced low-level westerly wind, and the East Asian summer monsoon (EASM), characterized by a pronounced low-level southerly wind (Wang et al., 2003). Recent climate change and related extreme weather events leading to catastrophic life and property loss in eastern Asia, particularly in China, necessitate water resource management and security measures which must take into account substantial regional and intraseasonal fluctuation in precipitation (Heng et al., 2020). The Yangtze River basin (YZRB) has complicated and unusual precipitation patterns and a unique regional climate, and it is a flood-prone area due to the influences of the East Asian and South Asian summer monsoons (Huang et al., 2021; Sutcliffe, 1987). The EASM, which is caused by a heat difference between the Pacific Ocean and the Asian mainland, is a significant component of inland eastern Asia's climate. The regional precipitation pattern in China, in particular, is significantly correlated with the EASM (Li et al., 2023). Precipitation is the primary factor influencing agricultural and economic development in the YZRB (Lijuan et al., 2018).

The El Niño–Southern Oscillation (ENSO) (McPhaden et al., 2006) is rooted in complex nonlinear large-scale interactions within and between the atmosphere and ocean circulation, and it causes a persistent abnormal fluctuation in sea surface temperature (SST) in the central and eastern equatorial Pacific. This fluctuation has a quasi-periodic character with a 2- to 7-year period (Wang, 2018). In the beginning, the notion of El Niño (EN) and the Southern Oscillation (SO) originated by figuring out a positive ocean–atmosphere feedback that triggers ENSO (Bjerknes, 1969). The initial warm SST anomaly in the eastern equatorial Pacific reduces the east–west SST gradient and slows the Walker circulation, culminating in the westerly wind anomaly in the central equatorial Pacific (Gill, 1980). The westerly wind anomaly, in turn, promotes a change in ocean circulation, exacerbating the SST anomaly. Positive feedback causes the tropical Pacific to warm, culminating in El Niño. Once El Niño develops, negative feedbacks are required to transition from a warm to a cold phase, a process called La Niña (Wingfield et al., 2018). Precipitation varies inextricably with internal and external oscillations in global sea surface temperature. The Pacific Ocean's alternate cycle of warming (El Niño) and cooling (La Niña) states affects interannual climate variability (Pui et al., 2012; Webster and Yang, 1992). ENSO impacts global climate through its teleconnections, which may serve as a reliable source of predictability (Horel and Wallace, 1981); however, they are highly sensitive to global temperature changes (Tsonis et al., 2003; Philip and van Oldenborgh, 2006; Zheng et al., 2016). Climate change poses a severe threat to China's water security as extreme precipitation events become more frequent, such as high-precipitation events in Beijing in 2012, and more recently in Henan in 2021, which resulted in billions of dollars in economic losses (Mingzhong et al., 2017; Li et al., 2019; Xie et al., 2015; Hsu et al., 2022). The long-term patterns in EASM rainfall in the Yellow River basin (YWRB) were driven by variations in air circulation over the Pacific Ocean, such as the ENSO cycle and the Pacific Decadal Oscillation (PDO) phase transition, which may thrive as measurable factors in the prediction of future EASM rainfall (Li et al., 2023). The links between extreme precipitation and ENSO depend on magnitude, regions, and seasons (Wei et al., 2012).

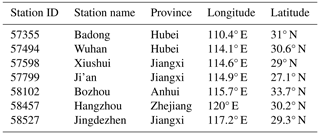
Several studies (Yang et al., 2005; Li and Zeng, 2013; Zhang et al., 2013, 2017; Xiao et al., 2015; Gao and Wang, 2017; Cao et al., 2017; Chang et al., 2016; Hardiman et al., 2018; Lv et al., 2019; Liu et al., 2020) have previously investigated the association between annual/seasonal precipitation variability and ENSO in the Yangtze and Yellow River basins of China. The current impact of ENSO on precipitation on various sub-basin to basin scales across China and the main river basins (Yangtze and Yellow) is summarized in Table 1. In addition to the aforementioned studies, other recent studies considered the combined influence of ENSO and North Atlantic Oscillation (NAO) or PDO on future ENSO projections (Qadimi et al., 2021; Alizadeh, 2022; C. Liu et al., 2023). Some studies propose the strengthening of ENSO events (Cai et al., 2021) in the 21st century due to global warming, while others expect ENSO weakening (Callahan et al., 2021).

Table 1 Short literature review. Previous studies regarding the impact of ENSO on annual and seasonal precipitation in Chinese regions. ^∗ Et: evapotranspiration; Ppt: precipitation; YWRB: Yellow River basin; YZRB: Yangtze River basin; ERB: East River basin.

Considering the quasi-cyclic character of ENSO, Jajcay et al. (2018) studied interactions between different quasi-periodic components of ENSO dynamics. They uncovered a complex causal network involving instantaneous phases and amplitudes of annual, quasi-biennial, and low-frequency (period 4–7 years) ENSO modes. The observed causal interactions lead to intermittent synchronization phenomena responsible for extreme ENSO events. In this study, we analyze the causal influence of instantaneous phases of ENSO oscillatory components on scales of precipitation variability in eastern China, using information-theoretic generalization of Granger causality. Previous studies were restricted to SST amplitude-based ENSO states and their influential role in large scale interactions and precipitation variability. The term “ENSO phases” is frequently used for three cases: high-amplitude positive ENSO+ (El Niño), high-amplitude negative ENSO- (La Niña), and low-amplitude neutral ENSO0. Here we will use the term “ENSO states” in order to avoid confusion with the instantaneous phases of ENSO oscillatory modes.

In the following sections we will describe the study area and the analyzed data. Then we will introduce the applied methods, from the scale-wise decomposition using the complex continuous wavelet transform (CCWT hereafter), to the conditional mutual information (CMI) as the causality measure and surrogate data method for assessing its statistical significance, to the conditional means defined as tools for estimating the effect of the uncovered causal relations in measurable physical quantities. Then we will present the results and their discussion.

2 Data and methods

2.1 Study area

The present study includes a particular area of China through which major Chinese rivers, the Yangtze and Yellow rivers, flow and ultimately drain into sea, as shown in Fig. 1. The Yangtze and Yellow rivers have distinct natural habitats and development demands, despite the fact that they both originate on the Qinghai–Tibet Plateau (Fang et al., 2021). The Yellow River, also known as China's Mother River, initiates in the Bayankala Mountains and travels eastward throughout the Loess Plateau (LP) and the North China Plain, eventually draining into the Bohai Sea. In accordance with a 1973 survey, the length of the Yellow River is 5464 km, and its basin area of 752 443 km² consists of three primary sub-basins: the Tibetan Plateau (TP), the LP, and the alluvial plateau in the east (Fu et al., 2004). The altitudes range from 2000 to 5000 m in the Tibetan Plateau in the western sections, which stretch from the Bayankala Mountains to the eastern estuary, and from 500 to 2000 m in the LP and in the alluvial plateau to the east.

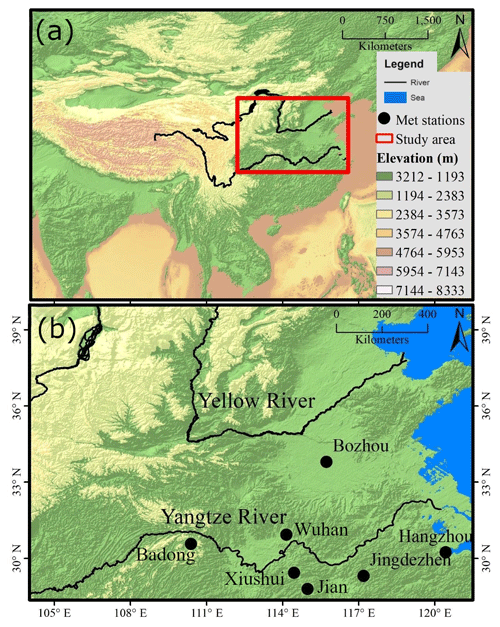
Figure 1 Study area. (a) Localization of the selected region in the Yangtze and Yellow River basins. (b) Detailed view of the study area, including the positions of selected stations.

The Yangtze River is China's longest river and the world's third largest, and it contributes considerably to China's equitable economic and ecological growth (Xiao et al., 2015). The ecological growth of the Yangtze River basin refers to the development and changes in its ecosystems over time, influenced by both natural processes and human activities. The Yangtze River basin has undergone significant ecological changes due to various factors, such as climate, geography, and human impact. The basin's high, middle, and lower portions have various climates and geomorphology, which contribute to its great biodiversity and huge number of uncommon and unique species (Chen, 2020). Therefore, its ecological growth is as important as its economic growth.

The Yangtze River's primary course commences at the TP and travels 6300 km east to the East China Sea. The YZRB is predominantly controlled by Siberian northwestern winter and southeastern summer monsoons. The winter monsoon brings cold, dry air from Siberia during the winter months. It has the potential to diminish temperatures and precipitation, resulting in drought conditions in certain areas of the basin (Yang et al., 2023). Yichang hydrological station (YHS) separates the Yangtze River into upper and lower sections and is renowned as the “Gateway to the Three Gorges”. The Three Gorges Dam (TGD) lies just approximately 40 km above (Xu et al., 2007). The territory above Yichang station is commonly regarded as the upper sub-basin of the YZRB, the region around Yichang station and Hukou station is the middle sub-basin, and the region under Hukou station is the lower sub-basin of the YZRB (Fang et al., 2018). The YZRB lies in a subtropical and temperate climate zone dominated by monsoonal winds; the southern region exhibits a subtropical climate, while the northern region is a temperate zone. Major flooding in the YZRB is linked with warm ENSO, and strong summer monsoons typically occur after El Niño conditions in the winter, while weak winter monsoons occur after La Niña (Xu et al., 2007). Our area of study covers the southeastern part of the YZRB.

2.2 Gridded data

We have used fifth-generation atmospheric reanalysis of the European Centre for Medium-Range Weather Forecasts (ECMWF), namely ERA5. The fifth generation was launched in 2017 by the Copernicus Climate Change Service (Jiang et al., 2021). Jiang et al. (2021) explicitly explained the advantages of ERA5 concerning advanced assimilation system and parameterization schemes as compared to the previously launched generations. Furthermore, the spatial and temporal range was improvised by enabling the hourly estimation at a horizontal resolution of 0.25° covering 137 vertical levels. The ERA dataset is on 1.5°×1.5° grids from 1979 to present. The SST over the tropical Pacific is based on the Hadley Centre sea ice and sea surface temperature data (HadISST) (Rayner et al., 2003). The top level is 0.01 hPa around 80 km above the ground surface. The ERA5 data are freely available for users. Our data range from 1951 to 2020 for the selected study area and were downloaded from https://cds.climate.copernicus.eu/datasets/reanalysis-era5-single-levels-monthly-means?tab=overview (last access: 11 January 2021).

Recently, some studies focused on comparing the performance of model-based precipitations such as ERA to satellite products for mainland Chinese regions and the Tibetan Plateau, since reliable precipitation retrievals with fine spatiotemporal resolutions are vital in global and regional evaluations (Xu et al., 2022; Hu and Yuan, 2021). Model-based precipitation estimates, which are an essential alternative to satellite-based precipitation products, have grown rapidly in recent decades. Model-based products outperform satellite products in subregions of temperate monsoon climate (TM) and temperate continental climate (TC) (Xu et al., 2022). However, when compared to gauge precipitation, ERA5 performance was being compromised in terms of frequency and intensity for the Tibetan Plateau (Hu and Yuan, 2021). The latter study further argued that rainfall gauges on the Tibetan Plateau are generally positioned in valleys and may not correctly reflect the region's average. Another study for the same regions of the TP and Sichuan observed that ERA-Interim exhibits better performance than IMERG_E, IMERG_L, IMERG_F, CHIRPS, TRMM_3B42, and TRMM_3B42RT (Lei et al., 2021). Future studies will require additional observations and clarification of station locations and higher levels (Hu and Yuan, 2021). ERA5 has replaced ERA-Interim, and this release offers several improvements over the previous ERA-Interim reanalysis solution due to improved design and generation methodologies. In comparison to ERA-Interim, this dataset is more advanced due to several factors, including a high resolution, day-by-day archiving, diverse data sources, better assimilation, and diversified data products (Tarek et al., 2020). The assessment of the monthly flood season (Lavers et al., 2022) indicates that ERA5 is slightly better than the other models. It is better in the extratropics. ERA5 precipitation has been found to be a sufficiently excessive source of information in the non-tropical areas. Therefore, it is suggested that ERA5 be utilized primarily for extratropical precipitation monitoring. ERA5 performs spatially across China, with the highest correlation coefficient values in eastern, northwestern, and northern China and the lowest biases in southeastern China (our study area) (Jiao et al., 2021). Similarly, intensity comparisons show strong agreement between ERA5 and EOBS in Germany, Ireland, Sweden, and Finland but some disagreement in places with scarce input stations (Rivoire et al., 2021).

Figure 2 illustrates the distribution of mean precipitation in the south of eastern China from 1951–2020, its standard deviation, and the relative difference of ENSO states. The mean precipitation is high in the southeastern part of the YZRB compared to the YWRB. It reaches its maximum limit of 8 mm d⁻¹ in some areas of the YZRB, while it remains in the lower range of 1.4 to 3.5 mm d⁻¹ in upper areas of the YWRB, as shown in Fig. 2a. The standard deviation, characterizing the overall precipitation variability, also exhibits the same pattern as the mean precipitation. The variability is higher in southeastern parts of the YZRB, whereas it is lower for the YWRB, as shown in Fig. 2b. It is interesting to assess the variability relative to mean precipitation; therefore the standard deviation divided by the mean precipitation is shown in Fig. 2d. The relative variability is much higher in the YWRB compared to the YZRB. It reaches the maximum level of 1.4 in most areas of the YWRB; however, it remains at 0.63 to 0.93 in the southeastern parts of the YZRB. For comparison, we map in Fig. 2c the difference between the ENSO positive and neutral states related to the mean precipitation. We observe that the relative difference is lower than the overall variability in the entire selected region but increases in the same southeastern parts of the YZRB with heavy precipitation, attaining the range of 0.17–0.31.

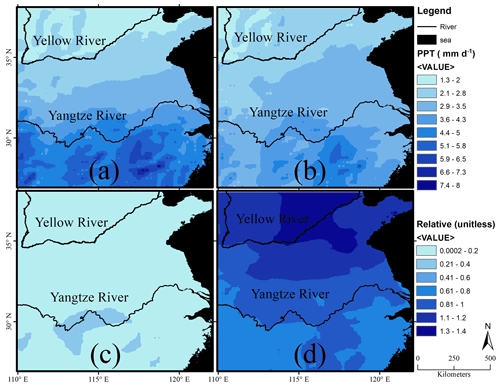
Figure 2 Precipitation and its variability in the study area. Spatial distribution of precipitation and its variability during 1951–2020: (a) mean precipitation, (b) precipitation standard deviation (SD), (c) relative difference between the ENSO positive and ENSO neutral state, and (d) relative precipitation SD (SD/mean precipitation).

2.3 Station data and EASM index

The observational data used in this paper are monthly precipitation records (from January 1955 to December 2016) provided by the National Meteorological Information Center of the China Meteorological Administration (https://data.cma.cn/data/detail/dataCode/A.0019.0001.S001.html, last access: 7 August 2017). The monthly East Asian summer monsoon index (from January 1948 to December 2015) is defined by Zhang et al. (2003).

2.4 ENSO data

The Niño 3.4 series was downloaded from https://psl.noaa.gov/gcos_wgsp/Timeseries/Data/nino34.long.data (last access: 11 May 2023). ENSO states were defined as warm (ENSO+) and cold (ENSO-) periods based on crossing the threshold of ±0.5 °C for the Oceanic Niño Index (ONI) (3-month running mean of ERSST.v5 SST anomalies in the Niño 3.4 region). Neutral ENSO0 means an ONI between ±0.5 °C. The ONI was obtained from https://origin.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ONI_v5.php (last access: 11 May 2023).

2.5 Scale-wise decomposition, instantaneous phases, and amplitudes

Consider a time series {x(t)}, $t=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{\dots },N$, here either monthly Niño 3.4 index or precipitation recordings, reflects dynamics on different timescales. The latter can be extracted; i.e., the time series can be decomposed using the complex continuous wavelet transform (CCWT hereafter) with the complex Morlet wavelet (Torrence and Compo, 1998):

$$\begin{array}{}\text{(1)}& \mathit{\psi }\left(t\right)={\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{2}\mathit{\pi }{\mathit{\sigma }}_t^{\mathrm{2}}}}}\exp \left(-{\displaystyle \frac{t^{\mathrm{2}}}{\mathrm{2}{\mathit{\sigma }}_t^{\mathrm{2}}}}\right)\exp \left(\mathrm{2}\mathit{\pi }ift\right),\end{array}$$

where $i=\sqrt{-\mathrm{1}}$, σ_t is the bandwidth parameter, and f is the central frequency of the wavelet. σ_t determines the rate of decay of the Gauss function, and its reciprocal value ${\mathit{\sigma }}_f=\mathrm{1}/\mathit{\pi }{\mathit{\sigma }}_t$ determines the spectral bandwidth. CCWT converts the time series x(t) into a set of complex wavelet coefficients W(t,f):

$$\begin{array}{}\text{(2)}& W(t,f)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\mathit{\psi }\left(t^{\prime }\right)x(t-t^{\prime })\mathrm{d}{t}^{\prime }.\end{array}$$

The central wavelet frequency f defines the related timescale. Due to the limited spectral bandwidth, we obtain an oscillatory quasi-periodic component W(t,f) reflecting temporal variability at that timescale. Using the analytic signal approach (Pikovsky et al., 2001), a complex oscillatory time series can be represented as

$$\begin{array}{}\text{(3)}& W(t,f)=s_f\left(t\right)+i{\widehat{s}}_f\left(t\right)=A_f\left(t\right)e^{i{\mathit{\varphi }}_f\left(t\right)},\end{array}$$

where $s_f\left(t\right)=\text{Real}\mathit{\left\{}W\right(t,f\left)\mathit{\right\}}$ and ${\widehat{s}}_f\left(t\right)=\text{Im}\mathit{\left\{}W\right(t,f_i\left)\mathit{\right\}}$.

$$\begin{array}{}\text{(4)}& {\mathit{\varphi }}_f\left(t\right)=\arctan {\displaystyle \frac{{\widehat{s}}_f\left(t\right)}{s_f\left(t\right)}}\end{array}$$

is the instantaneous phase, and

$$\begin{array}{}\text{(5)}& A_f\left(t\right)=\sqrt{s_f(t{)}^{\mathrm{2}}+{\widehat{s}}_f(t{)}^{\mathrm{2}}}\end{array}$$

is the instantaneous amplitude of the oscillatory component W(t,f). Paluš (2014) describes how the instantaneous phases and amplitudes can be used to uncover causal cross-scale information transfer.

2.6 Conditional mutual information as a causality measure

Paluš (2014) describes in detail the use of the conditional mutual information as a causality measure for inferring cross-scale causal relations. Here we briefly remind the basic ideas.

Mutual information I(X;Y) of two random variables X and Y is defined as $I(X;Y)=H\left(X\right)+H\left(Y\right)-H(X,Y)$, where the entropies H(X), H(Y), and H(X,Y) are given in the usual Shannonian sense (Cover and Thomas, 1991). The conditional mutual information $I(X;Y|Z)$ of the variables X and Y given the variable Z is defined using the conditional entropies (Cover and Thomas, 1991; Paluš, 2014) as

$$\begin{array}{}\text{(6)}& I(X;Y|Z)=H(X\left|Z\right)+H\left(Y\right|Z)-H(X,Y\left|Z\right).\end{array}$$

Consider two time series {x(t)} and {y(t)} regarded as realizations of two stationary ergodic stochastic processes, {X(t)} and {Y(t)}, which represent observables of two possibly coupled systems. Alternatively, the time series {x(t)} and {y(t)} can be understood as one-dimensional projections of trajectories of dynamical systems $\dot{\mathit{X}}=f_X(\mathit{X},\mathit{Y})$ and $\dot{\mathit{Y}}=f_Y(\mathit{Y},\mathit{X})$, where X and Y are vectors of dimensions d₁ and d₂, respectively.

Paluš et al. (2001) proposed to measure the information transferred from system (process) {Y(t)} to system (process) {X(t)} using the conditional mutual information $I(\mathit{Y};{\mathit{X}}_{\mathit{\tau }}|\mathit{X})$, where X=X(t) and ${\mathit{X}}_{\mathit{\tau }}=\mathit{X}(\mathrm{t}+\mathit{\tau })$.

Using the idea of Markov processes, Schreiber (2000) introduced a functional of conditional probability distributions called transfer entropy. Paluš and Vejmelka (2007) show that the transfer entropy is equivalent to CMI $I(\mathit{X};{\mathit{Y}}_{\mathit{\tau }}|\mathit{Y})$. Barnett et al. (2009) show analytically that the transfer entropy (i.e., CMI $I(\mathit{X};{\mathit{Y}}_{\mathit{\tau }}|\mathit{Y})$) is equivalent to Granger causality for Gaussian processes. Therefore, causal influence is frequently interpreted as information transfer, or directed information flow. However, it is worth noting that this interpretation of the term “information flow” might not be compatible with the term meaning in information physics (Perdigão et al., 2020; Hall and Perdigão, 2021) or in the theory of dynamical systems where the information flow can be derived from system equations (Liang, 2013).

If the measurement of information about the future X_τ of the process {X}, with τ time units shifted forward (“τ-future” hereafter), contained in the process {Y} is used for testing the existence of a causal link from {Y} to {X}, denoted as Y→X, Paluš and Vejmelka (2007) show that the vectors X and Y_τ can be substituted by one-dimensional components x and y_τ, and the CMI in the time series representation reads as

$$\begin{array}{}\text{(7)}& I\left(y\right(t);x(t+\mathit{\tau }\left)\right|x\left(t\right),x(t-{\mathit{\eta }}_{\mathrm{1}}),\mathrm{\dots }x(t-(d_{\mathrm{1}}-\mathrm{1}\left){\mathit{\eta }}_{\mathrm{1}}\right)).\end{array}$$

The condition in CMI (Eq. 7) must contain complete information about the state of the system X (Paluš and Vejmelka, 2007). According to the theorem of Takens (1981), the state of a d₁-dimensional dynamical system (a point in the state space) is mapped by the set of time-lagged coordinates $x\left(t\right),x(t-{\mathit{\eta }}_{\mathrm{1}}),\mathrm{\dots }x(t-(d_{\mathrm{1}}-\mathrm{1}\left){\mathit{\eta }}_{\mathrm{1}}\right)$, where η₁ is the backward time lag used in the embedding of system X. This time lag can be set according to the embedding construction recipe based on the first minimum of the mutual information (Fraser and Swinney, 1986).

The causal link X→Y is tested in analogy with Eq. (7):

$$\begin{array}{}\text{(8)}& I\left(x\right(t);y(t+\mathit{\tau }\left)\right|y\left(t\right),y(t-{\mathit{\eta }}_{\mathrm{2}}),\mathrm{\dots }y(t-(d_{\mathrm{2}}-\mathrm{1}\left){\mathit{\eta }}_{\mathrm{2}}\right)).\end{array}$$

For estimating the information transfer delay, Wibral et al. (2013) proposed the following CMI reformulation:

$$\begin{array}{}\text{(9)}& {\displaystyle }\begin{array}{rl}{\displaystyle }I\left(x\right(t);& {\displaystyle }y(t+\mathit{\tau })\left|y\right(t+\mathit{\tau }-\mathrm{1}),\\ {\displaystyle }& {\displaystyle }y(t+\mathit{\tau }-\mathrm{1}-{\mathit{\eta }}_{\mathrm{2}}),\mathrm{\dots }y(t+\mathit{\tau }-\mathrm{1}-(d_{\mathrm{2}}-\mathrm{1}\left){\mathit{\eta }}_{\mathrm{2}}\right)),\end{array}\end{array}$$

in which the condition moves forward with the increasing prediction horizon τ, while, in the formulation of Paluš and Vejmelka (2007), the condition is kept in the same position for all values of τ. The Wibral et al. (2013) formula (Eq. 9) is used in order to establish the causal delay, while Eq. (7) and Eq. (8) are used for testing the statistical significance of uncovered causal relations. The Wibral et al. (2013) formula (Eq. 9) was proposed as a CMI in the case of self-prediction optimality (SPO) of y states prior to the forecast delay τ. This is a very conservative estimate of CMI/TE, since the SPO may never be reached with CMI/TE of Eq. (9) being underestimated. CMI estimated according to Eq. (7) or (8) is more sensitive with respect to the detection of causality.

For testing the cross-scale causality, before applying Eq. (8), the Niño 3.4 and the precipitation data underwent CCWT, x(t) was substituted by the ENSO phase ${\mathit{\varphi }}_{f_i}\left(t\right)$ for a particular frequency f_i, and y(t) was substituted by the precipitation amplitude $A_{f_j}\left(t\right)$ for a frequency f_j. The Gaussian estimator was used and d₂=3 was chosen as in Paluš (2014) based on “saturation of the results”, i.e., obtaining unchanged results for d₂=4 in comparison with d₂=3. The tested value is the CMI average for time lags τ=1 to 6 months, according to the recommendation in Paluš and Vejmelka (2007).

2.7 Surrogate data for statistical testing

Finite-sample estimates of mutual information are always nonzero. In order to assess the presence of causal relations in the analyzed data, it is suitable to relate the CMI values computed from studied data to ranges of CMI values obtained from uncoupled processes that share statistical properties of the analyzed data. Using the surrogate data testing procedure, we manipulate the original data in a randomization procedure that preserves the original frequency spectra or variance on all relevant timescales. In this study, we use the circular time-shifted surrogate data, proved effective for the inference of causality (Manshour et al., 2021). For the analyzed time series X of the length N, we generate 100 independent realizations of time-shifted surrogates as follows: for each realization, an integer variable k<N is randomly chosen. Then, by moving the first k values of X(1),X(2)…X(k) to the end of the time series, we generate the circular time-shifted surrogate series X^surr as

$$\begin{array}{}\text{(10)}& {\displaystyle }\begin{array}{rl}{\displaystyle }& {\displaystyle }{X}^{\text{surr}}=\\ {\displaystyle }& {\displaystyle }\mathit{\left\{}X\right(k+\mathrm{1}),X(k+\mathrm{2}),\mathrm{\dots },X(N),X(\mathrm{1}),X(\mathrm{2}),\mathrm{\dots },X(k\left)\mathit{\right\}}.\end{array}\end{array}$$

In order to avoid surrogates very close to the original series, or an influence of seasonality, k is constrained as follows: $min(k,N-k)>\mathrm{200}$ and $\mathrm{3}<\text{mod}(k,\mathrm{12})<\mathrm{10}.$ The results of the surrogate data tests can be represented as the Z-score; e.g., for CMI, marked as I, it is

$$\begin{array}{}\text{(11)}& Z={\displaystyle \frac{I_d-\stackrel{\mathrm{‾}}{I_s}}{{\mathit{\sigma }}_s}},\end{array}$$

where I_d is the CMI value estimated from the studied data, $\stackrel{\mathrm{‾}}{I_s}$ is the mean for 100 realizations of the surrogate data, and ${\mathit{\sigma }}_s^{\mathrm{2}}$ is their variance. Typically, the results are considered statistically significant for Z>2. In the cross-scale analyses, the surrogate data are applied directly to the raw data before the application of the wavelet transform, using different shifts for the phase and amplitude series.

2.8 Conditional means as the effect size

The results reported below present statistical evidence of the cross-scale causal influence of ENSO on precipitation variability in eastern China. In order to quantify this causal effect in a measurable physical quantity and compare it with the effect of the amplitude-based ENSO states, we employed the method of conditional means (CM) (Jajcay et al., 2016), illustrated in Fig. 3. A segment of Niño 3.4 time series data is shown in black in Fig. 3a, while the ENSO states are marked by color: light red is used for El Niño, i.e., the ENSO positive state; light blue is used for La Niña, i.e., the ENSO negative state; and white is used for the ENSO neutral state given by the Oceanic Niño Index between −0.5 and 0.5. The Niño 3.4 time series (black) is plotted again in Fig. 3b together with its CCWT-extracted 6-year oscillatory component (blue curve) and the instantaneous phase (red saw-like pattern) of the latter. In each cycle, the phase rises from −π to π (note that the data in Fig. 3b are normalized for the common scale plot). However, the angular range of one cycle (2π) is only approximately equal to 6 years; i.e., the cycle period is variable within a small range given by the CCWT bandwidth. Each cycle of 2π radians is divided into six equidistant bins (different colors and patterns in Fig. 3c and d). Thus, each bin is only approximately equal to 1 year in real time. The phase bins are used to compute precipitation conditional means in order to see patterns of precipitation variability related to the considered ENSO cycle. The conditional mean for a particular bin is obtained by averaging precipitation data (from a particular station or a grid point) belonging to that bin in all cycles, e.g., the averaging runs over all blue bins over the whole dataset (see Fig. 3d for a subset of the data).

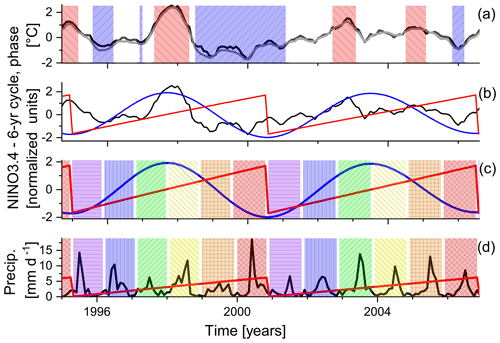
Figure 3 ENSO states and binning of the low-frequency cycle. From top to bottom: (a) a segment of anomalized Niño 3.4 (black) and ONI (gray) time series with marked ENSO states – warm episodes ENSO+ (light red), cold episodes ENSO- (light blue), and neutral ENSO0 (white). (b) The same segment of the anomalized Niño 3.4 time series (black) with its CCWT-extracted 6-year component (blue) and the instantaneous phase (red) of the latter. (c) The 6-year Niño 3.4 component (blue) and its instantaneous phase (red). The bars of different colors and patterns mark the six phase bins into which each 6-year cycle is divided. (d) A segment of reanalysis precipitation data from the grid point 33.75° N, 115.75° E (black) and the 4-month lagged phase (red) of the 6-year Niño 3.4 cycle and related phase bins (bars of different colors and patterns) in which the precipitation conditional means are computed.

Computing the conditional means, the precipitation time series is not exactly aligned in time with the ENSO states or the ENSO phase bins, since the causal effect of ENSO can occur with some time delay. The causal delay can be found in the causality analysis as follows: in Fig. 4a, the conditional mutual information represents the causal influence of ENSO states on the precipitation (EASMI-ZQY index). It was computed using the Wibral et al. (2013) formula (Eq. 9) in which x(t) is a discrete three-value function of the ENSO states, y(t) is the precipitation EASMI-ZQY index discretized into four bins using the equiquantal binning algorithm (Paluš and Vejmelka, 2007), and d₂=1. It is plotted as a function of causal delay. The blue line shows the causal influence in the direction from ENSO to precipitation, while the dashed black line shows the causal influence of the precipitation on the ENSO states. The significance level is shown by the red line. It is evident that there is no significant causality from precipitation to ENSO; however, the influence of ENSO exhibits a significant peak for the time lag of 6 months. Therefore, in computing the conditional precipitation means for the ENSO states, precipitation data are advanced by 6 months.

Figure 4 Causal mechanisms and their effects. (a) Conditional mutual information measuring the causal influence of ENSO states on precipitation characterized by the EASMI-ZQY index (solid blue line) and causality in the opposite direction (dashed black line). The red line is the significance threshold given as the mean+2SD for the surrogate data. (b) Conditional means for the precipitation data from the grid point 33.75° N, 115.75° E for the different ENSO states, ENSO- (light blue), ENSO0 (white), and ENSO+ (light red), computed for the lag of 6 months. Differences between the adjacent states are in black. (c) Evaluation of statistical significance of the maximum relative difference between states, ENSO- and ENSO0 (vertical red line), using the histogram for the surrogate data (black). (d) Conditional mutual information measuring the causal influence of the ENSO 6-year cycle phase on the 2-year cycle amplitude for precipitation characterized by the EASMI-ZQY index (solid blue line) and causality in the opposite direction (dashed black line). The red line is the significance threshold given as the mean+2SD for the surrogate data. (e) Conditional means for the precipitation data from the grid point 33.75° N, 115.75° E for the six phase bins within the ENSO 6-year cycle (various colors). Differences between adjacent bins (red) are regarded as the amplitude of the precipitation quasi-biennial cycle. The effect of the 6-year cycle phase is estimated as the maximum difference of the bin values – here, the difference between the values of the sixth (light red) and third (green) bins. This value relative to the total precipitation mean is 0.264 and is marked by the vertical red line in panel (f) and found statistically significant in comparison with the surrogate histogram (black).

Figure 4b represents the conditional means, i.e., the average precipitation for the ENSO states using the precipitation data at the grid point (33.7° N, 115.75° E). The three ENSO states, i.e., negative, positive, and neutral, are shown with light-blue, light-red, and white bars, respectively. The differences between the two adjacent states are marked with black bars. The first black bar represents the difference between the negative and neutral ENSO states, while the next one exhibits the difference between the positive and neutral ENSO states. The maximum difference, expressed as a relative value (the difference divided by the average precipitation), is equal to 0.259, which is shown by the vertical red line in Fig. 4c, while the black line illustrates the histogram of the same differences obtained from the surrogate data. It can be observed that the red bar lies inside the surrogate histogram which means the difference between two ENSO states is not statistically significant in this grid point.

Figure 4d shows the conditional mutual information showing the causal influence of the phase of the 6-year component obtained from the Niño 3.4 time series, on the precipitation amplitude for the variability in the quasi-biennial scale (blue). It was again computed using the Wibral et al. (2013) formula (Eq. 9); however, since the cross-scale causality is evaluated, before applying Eq. (9), the Niño 3.4 and the precipitation data underwent CCWT, x(t) was substituted by the ENSO phase ${\mathit{\varphi }}_{f_i}\left(t\right)$ for a particular frequency f_i, and y(t) was substituted by the precipitation amplitude $A_{f_j}\left(t\right)$ for a frequency f_j. The Gaussian estimator was used and d₂=3 was chosen as in Paluš (2014). It is evident again that there is no significant causality from the precipitation to the ENSO phase shown by the dashed black line. However, the influence of the ENSO phase on the amplitude of precipitation exhibits a clear significant peak in approximately 4 months (lags 2–6 months). Therefore, for the calculation of conditional means for the six phase bins, we used the ENSO phase bins with a time shift of 4 months back relative to precipitation data. Figure 4e represents the results of conditional means computed in different ENSO phase bins, marked by different light colors, while differences between the adjacent bins are displayed as red bars.

In order to evaluate the influence of the low-frequency ENSO mode on precipitation, the difference is taken between the maximum and minimum of the conditional means in the six phase bins. Here, again expressed as the relative value, it is 0.264, and is illustrated by the vertical red line in Fig. 4f. The histogram obtained from the surrogate data using the same procedure shows this value outside the surrogate distribution. Thus, the effect of the slow ENSO cycle on precipitation in this grid point is statistically significant.

Table 2 Geographical coordinates of seven local precipitation stations used in the combined region of the Yellow and Yangtze River basins.

3 Results

The cross-scale causal influence of ENSO on eastern Chinese precipitation, measured as the information transfer from the time series of the instantaneous phase of an oscillatory ENSO component to the time series of the instantaneous amplitude of a precipitation oscillatory component, was evaluated using conditional mutual information and a surrogate data testing approach (see Methods) and is presented in Fig. 5. The ENSO phase for a particular timescale was extracted from the Niño 3.4 index using complex continuous wavelet transform. Similarly, the precipitation amplitude for a particular timescale was also extracted using the CCWT for the relevant central period from the EASMI-ZQY index, from station precipitation data, or from reanalysis data. Firstly, we evaluate the causal ENSO effect on the Eastern Asian summer monsoon index characterizing the whole eastern China region: the EASMI-ZQY index (Zhang et al., 2003) (Fig. 5a). The dominant patterns of statistically significant causality have been identified as an influence of the phase of the ENSO oscillatory component with the period close to 2 years (quasi-biennial, or QB component hereafter) on the amplitude of the annual cycle in the precipitation index and related variability on the timescale close to 1 year (quasi-annual, or QA variability hereafter). The QA precipitation variability is also influenced by slower ENSO oscillations with periods between 4 and 6 years. Another identified area of the cross-scale phase–amplitude causality is the influence of the slow ENSO modes (periods starting under 5 and ending over 6 years) on the biennial and quasi-biennial precipitation variability. The results from the EASMI-ZQY index are, to various extents, repeated in the precipitation data of individual stations. For instance, in the precipitation data from Hangzhou station 58457 in Zhejiang (Fig. 5c), we can see some influence of the ENSO QB and slow modes on the QA precipitation variability and a marked influence of the phase of the low-frequency ENSO modes (periods between 5 and 7 years) on the amplitude of QB precipitation variability. In the precipitation data from Bozhou station 58102 in Anhui (Fig. 5e), the amplitude of the precipitation QB variability is influenced by a broadband low-frequency (LF) ENSO oscillatory mode with periods from 3 to 7 years. In all figures but Fig. 5b, we can see a number of small spots of false positive results which occur due to multiplicity of the tests in the phase period × amplitude period plane. This effect can be partially attenuated by taking an average of results from several stations, such as the results in Fig. 5b. The only spots of significant causality which survived the averaging give the influence of the ENSO QB mode on the precipitation QA variability and the influence of the ENSO low-frequency mode in a period of around 6 years on the amplitude of the QB precipitation variability.

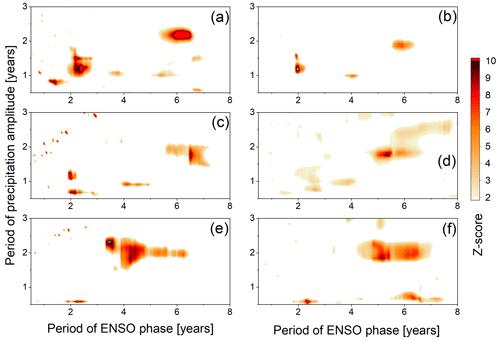
Figure 5 Cross-scale ENSO influence on precipitation in eastern China. Cross-scale phase–amplitude information transfer characterizing the causal influence of the phase of ENSO oscillatory components, with periods given on the abscissa, on the amplitude of precipitation oscillatory components, with periods given on the ordinate. Significant causal influence of ENSO detected in (a) the EASMI-ZQY index; (b) precipitation data from six stations in Hubei, Jiangxi, and Zhejiang (see Table 2, averaged results); (c) precipitation data from station 58457 Hangzhou in Zhejiang; (d) precipitation data from station 58527 Jingdezhen in Jiangxi; (e) precipitation data from 58102 Bozhou station in Anhui; and (f) ERA5 reanalysis precipitation data from the grid point 33.75° N, 115.75° E. The color codes present the conditional mutual information Z-score for Z>2, obtained in the test using 100 realizations of surrogate data.

The reported results present statistical evidence of the cross-scale causal influence of ENSO on precipitation variability in eastern China. In order to quantify this causal effect and compare it with the effect of the amplitude-based ENSO states, we employed the method of conditional means (CM) (Jajcay et al., 2016), illustrated in Fig. 3.

The conditional means of precipitation, conditioned either on the ENSO states or on the six phase bins and derived from the instantaneous phase of the low-frequency ENSO component with a period of around 6 years, were computed and their maximum differences were statistically evaluated for all grid points in the selected area and mapped in Fig. 6. Thus, Fig. 6 illustrates two different approaches to measure the causal effect of ENSO on precipitation in southeastern China. Figure 6a represents the map of the maximum relative difference (RD) in the six phase bins, while Fig. 6b shows the maximum RD between ENSO states (positive, negative, and neutral). In order to see the causal effects in physical quantities, Fig. 6c and d represent absolute values for the same variables as selected in Fig. 6a and b.

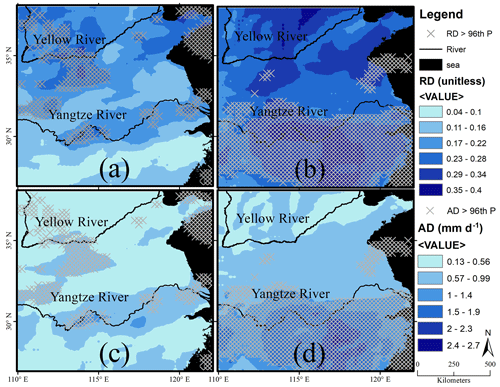
Figure 6 Quantification of the effects of two causal mechanisms. Relative (a, b) and absolute (c, d) maximum differences between precipitation conditional means: (a, c) conditioning on the six phase bins, i.e., the effect of the phase of the low-frequency ENSO component on precipitation, and (b, d) conditioning on the three ENSO states, i.e., the effect of the ENSO amplitude on precipitation. Statistically significant differences are marked with X.

In Fig. 6b and d, we evaluate the influence of ENSO states; i.e., from the point of view of ENSO oscillatory dynamics, it is the influence of the ENSO amplitude on precipitation. The values of RD are high and statistically significant in the south of the YZRB (Fig. 6b and d), while, in the case of the influence of the phase of low-frequency modes of ENSO, the significant areas are located mainly around the YWRB (Fig. 6a and c).

Extending the circle of investigation, we further observed the values and the occurrence of maxima and minima of the precipitation conditional means in relation either to ENSO states or to the six phase bins of the low-frequency ENSO component phase. Considering the ENSO states, the precipitation conditional means maxima, expressed relatively to the total mean, peak in the YZRB with ranges from 1.08 to 1.23 (Fig. 7a), while the minima range from 0.8 to 0.9 for the entire study area but increase at a few locations of the lower YZRB (Fig. 7b). Answering the question of in which ENSO state the precipitation conditional means maxima occur, the ENSO positive state dominates, mainly in the YZRB, while in the YWRB the maxima occur in the ENSO negative state (Fig. 7c). The precipitation conditional means minima occur exclusively in the ENSO neutral state (Fig. 7d).

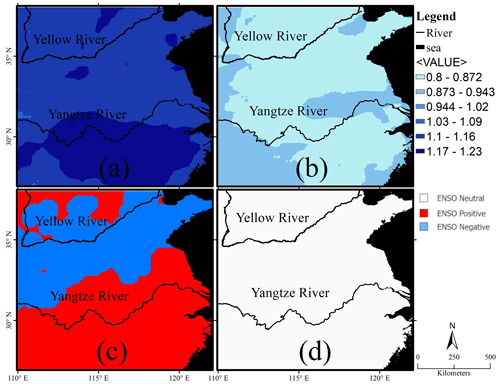
Figure 7 Geography of ENSO amplitude influence. Maximum and minimum precipitation values in ENSO states: (a) maximum precipitation value, (b) minimum precipitation value, (c) ENSO state in which maximum precipitation occurs, and (d) ENSO state in which minimum precipitation occurs.

Considering the six phase bins of the ENSO low-frequency component and the precipitation conditional means maxima, expressed relatively to the total mean, the highest values ranging from 1.1 to 1.23 dominate the YWRB region. Only a few areas in the YZRB reach this range, while most of the YZRB study area receives values from 1.03 to 1.09 (Fig. 8a). This is another piece of evidence suggesting that the dominant ENSO causal mechanism in the YWRB area is due to the phase of the low-frequency ENSO component and not due to the ENSO amplitude, in addition to the areas of statistically significant differences in Fig. 6a and c.

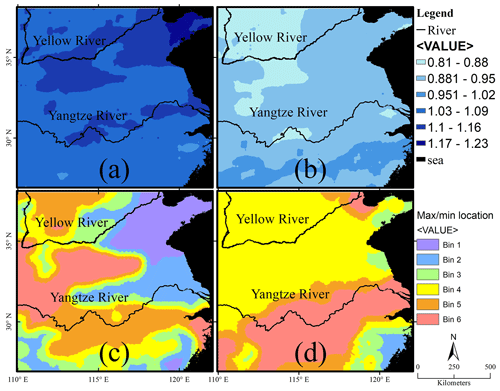
Figure 8 Geography of ENSO phase influence. Maximum and minimum precipitation values in the six phase bins given by the low-frequency ENSO phase: (a) maximum precipitation value, (b) minimum precipitation value, (c) ENSO phase bin in which maximum precipitation occurs, and (d) ENSO phase bin in which minimum precipitation occurs.

The precipitation conditional means minima peak in the lower reaches of the YZRB ranging from 0.96 to 1.02, while the lowest values under 0.89 are confined to the northwestern quadrant of the study area. In the majority of the study area, the values range from 0.89 to 0.95 (Fig. 8b). Discussing the occurrence of CM extrema within the LF cycle, we can refer to bin numbers, or divide the cycle into three states, using the term negative state for bins 1 and 6 at the edge of the cycle reaching cycle minima, positive state for central bins 3 and 4 where the cycle peaks, and neutral state for bins 2 and 5 (see Fig. 3c). In the YZRB and south of it, the minima occur in phase bins 2, 5, and 6 (Fig. 8d); that is, in neutral and negative states of the low-frequency ENSO component (cf. Fig. 3c). In the YWRB and adjacent areas, the minima are located in the positive state of the low-frequency cycle (bins 3 and 4; see Fig. 8d ; cf. Fig. 3c). The pattern of localization of the precipitation conditional means maxima in the six phase bins is more complex (Fig. 8c). For better understanding, we present precipitation conditional means in all six phase bins for selected grid points in Fig. 9.

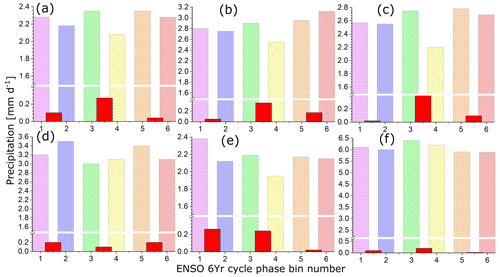
Figure 9 Local ENSO phase effects. Precipitation conditional means in the six ENSO phase bins at various coordinates: (a) 36° N, 110° E; (b) 33° N, 114° E; (c) 36° N, 111° E; (d) 33° N, 120° E; (e) 36° N, 117° E; and (f) 28° N, 117° E. Red represents the difference between two adjacent bins.

The results for a representative grid point from the YWRB, markedly influenced by the phases of ENSO oscillatory components, are presented in Fig. 9a. Since each of the six phase bins covering the 6-year cycle represents approximately 1 year in real time, the conditional means can be regarded as an estimate of the amplitude of the precipitation annual cycle (APAC). At first sight, one can see an alternation of higher and lower APAC, confirming the well-known alternation of strong and weak monsoon years (Meehl, 1987). The cross-scale causality analysis presented above suggests that this phenomenon is a consequence of the causal influence of the phase of the ENSO quasi-biennial component on the precipitation annual cycle amplitude. Differences between two adjacent APACs are illustrated by the red bars. The latter can be understood as an estimation of the amplitude of the precipitation quasi-biennial cycle (APQBC). Apparently, the APQBC is modulated by the low-frequency (LF; approximately 6-year) ENSO component. The maximum APQBC is in the middle, i.e., in the positive state of the LF ENSO cycle (cf. Fig. 3c). This is why both minimum and maximum precipitation conditional means occur in the positive state of the LF ENSO cycle in this area. Moving southeastward within the YWRB area, the behavior of CM is slightly different (Fig. 9b), reminding us that the ENSO component driving APAC is not exactly biennial but quasi-biennial. Its interactions with the precipitation annual cycle lead to frequent phase shifts, disturbing or reversing the weak–strong monsoon year alternation sequence. The minimum CM remains in the positive state of the LF ENSO cycle; however, the maximum CM moves to the last bin, number 6, i.e., to the negative state of the LF ENSO cycle. Let us be reminded that the maximum CM given by the ENSO state is located in the ENSO negative state in this area. The CM patterns in the next three points (Fig. 9c–e) are similar, with the minimum CM in the positive state of the LF ENSO cycle (middle bins 3 and 4), while the maximum CMs are located either in the negative (bins 1 and 6) or neutral (bins 2 and 5) state of the LF ENSO cycle.

The strength of the influence of the ENSO LF mode on the APQBC determines the location of precipitation CM extrema within the LF cycle. The strongest synchronization of the APQBC with the ENSO LF mode can be seen in Fig. 9a. Due to the markedly largest APQBC in the positive state of the LF cycle, both the precipitation minimum and maximum occur there (bins 3 and 4). With weaker synchrony, the precipitation maximum moves to the neutral or negative state of the LF cycle, while the minimum is kept in the positive state.

On the other hand, in the grid point located south of the Yangtze River, there is practically no modulation of the CM by the ENSO oscillatory components (Fig. 9f). The maximum CM is located in the positive phase, while the minimum CM is located in the neutral phase of the LF ENSO cycle. Let us be reminded that this is the area where the causal effect of the ENSO amplitude dominates, and CMs, conditioned on the ENSO states, reach maxima in the ENSO positive state and minima in the ENSO neutral state.

4 Conclusions

The El Niño–Southern Oscillation (ENSO) is an important global climate variability mode influencing precipitation in the Yangtze (YZRB) and Yellow (YWRB) river basins of eastern China. Considerable effort has been expended to analyze and describe this influence; see Table 1 and related references (Yang et al., 2005; Li and Zeng, 2013; Zhang et al., 2013, 2017; Xiao et al., 2015; Gao and Wang, 2017; Cao et al., 2017; Chang et al., 2016; Hardiman et al., 2018; Lv et al., 2019; Liu et al., 2020). In such analyses, ENSO, as the cause variable, is characterized using SST-based indices and/or ENSO states, derived from these indices or their anomalies. ENSO is a recurring phenomenon, regarded as an irregular oscillation with variable period and amplitude. Jajcay et al. (2018) decomposed the ENSO dynamics into quasi-periodic modes which mutually interact and temporarily synchronize, giving the rise to extreme ENSO events. In this study, we analyze the possible causal influence of instantaneous phases of ENSO oscillatory components, extracted from the Niño 3.4 index using the complex continuous wavelet transform (CCWT), on precipitation variability at different timescales. The precipitation data from eastern China are also decomposed using CCWT. We have detected, with statistical significance, a causal influence of the phase of the ENSO quasi-biennial (QB) mode on the amplitude of the precipitation annual cycle. As the second statistically significant causal relation, the amplitude of the precipitation QB mode is influenced by the phase of the ENSO low-frequency (LF) mode with periods between 4 and 7 years, mostly concentrated around the period of 6 years.

The conditional mutual information with the surrogate data testing provides statistical evidence for the existence of the causal relations described above. In order to estimate their effect in physical quantities, we employ the method of conditional means (CM) (Jajcay et al., 2016). Precipitation CM were conditioned on the ENSO states (positive, negative, and neutral), thus estimating the causal effect of the ENSO amplitude, or the effect of phases was assessed by dividing the LF (approximately 6-year period) ENSO cycle into six bins equidistantly defined using the phase of the ENSO LF mode. The instantaneous phases of the ENSO oscillatory modes are found the principal cause influencing the precipitation variability in the YWRB area. In the YZRB and adjacent areas, the ENSO amplitude dominates the causal influence on the precipitation variability. In the latter area, the phase-conditioned CMs do not reflect any influence of the ENSO oscillatory modes, and CM maxima and minima occur in positive and neutral states, respectively, of the LF ENSO mode, in agreement with the culmination of the precipitation maxima in ENSO positive states and the occurrence of precipitation minima in the ENSO neutral states.

On the other hand, in the YWRB, the phase-conditioned CMs are modulated by both QB and LF ENSO modes. The cross-scale information flow from the QB mode to the amplitude of the precipitation annual cycle causes the alternation of strong and weak monsoon years (Meehl, 1987). The timescale of this cause is not exactly biennial but quasi-biennial; therefore its interactions with the precipitation annual cycle lead to frequent phase shifts, disturbing or reversing the weak–strong monsoon year alternation sequence. The differences between the adjacent CM represent the amplitude of the precipitation QB mode, which is apparently modulated by the LF (approximately 6-year) ENSO mode. The strength of this modulation determines the position of precipitation CM maxima within the ENSO LF cycle, while the precipitation CM minima occur in the positive state of the ENSO LF cycle. When the precipitation CM are evaluated using the ENSO states, the minima are located in the ENSO neutral and the maxima are located in the ENSO negative state. This inconsistency can be explained by the observation (see Fig. 4 in Jajcay et al., 2018) that the ENSO extreme events do not necessarily coincide with the minima or maxima of the ENSO LF cycle but are determined by intermittent synchronization of ENSO QB modes.

Some recent studies (Yu et al., 2022a, b) report a robust contribution of the Tropospheric Biennial Oscillation (TBO) to the East Asian summer monsoon transitions. The relation between the TBO and the QB mode extracted from the ENSO dynamics is a challenge for further research. Other studies, e.g., Xiao et al. (2015), observed that, besides ENSO, the North Atlantic Oscillation, Indian Ocean Dipole, and Pacific Decadal Oscillation also have an effect on seasonal precipitation regimes in the Yangtze River basin. Our cross-scale information flow detection method can also be used to establish a causal relationship between precipitation and other large-scale climate variability modes, or it can be applied to uncover causal interactions in diverse Earth science problems involving multiple timescales. In a broader perspective, the framework we used here is applicable to analyzing phenomena across a wide range of disciplines; for example, in neuroscience, the cross-frequency phase–amplitude coupling has recently been observed in electrophysiological signals reflecting the brain dynamics (Canolty and Knight, 2010), and the conditional mutual information has proven to be a robust tool for its detection (Arinyo-i-Prats et al., 2024).

The fact that complex evolution of climate, atmosphere, or circulation regimes is influenced by interactions of dynamics on multiple timescales is known (Muñoz et al., 2017; Zhang et al., 2023). For instance, Muñoz et al. (2015) suggest that cross-timescale interactions between different climate drivers improve the predictive skill of extreme precipitation. Hsu et al. (2023) show that multiscale interactions (in particular, scale interactions between the monsoon mean field, two modes of intraseasonal oscillation, and synoptic disturbances) drove the devastating floods in Henan, China, during July 2021. J. Liu et al. (2023) used the multiscale window transform (MWT) and MWT-based energy and vorticity analysis (MS-EVA) to identify three scale fields: basic flow fields (>64 d), intraseasonal oscillation fields (8–64 d), and synoptic-scale eddy fields (<8 d), responsible for the torrential rainfall event which hit Zhengzhou on 20 July 2021. Ungerovich et al. (2023) emphasize the role of the large-scale circulation anomalies associated with ENSO teleconnections in the simulation of extreme rainfall events in Uruguay, while Pineda et al. (2023) suggest that the early onset of heavy rainfall on the northern coast of Ecuador in the aftermath of El Niño 2015/16 was favored by the convective environment in late January due to cross-timescale interference of the very strong El Niño event and a strong and persistent Madden–Julian oscillation. The presented research, however, is a first step in developing a methodology able to establish solid statistical evidence for existence of cross-scale causal interactions and to estimate their effect in measurable physical quantities. In particular, the results presented here can open new doorways in understanding and predicting precipitation anomalies in eastern Asia. Although physical mechanisms explaining the observed cross-scale information transfers are yet to be established, the uncovered causal relations can already be used in statistical or machine learning tools to forecast precipitation anomalies. In related considerations, Muñoz et al. (2023) propose to find “windows of opportunity” in forecasts across timescales by combining wavelet spectral analysis and a non-stationary time–frequency causality analysis. Materia et al. (2024) try to understand the causal factors behind these windows of opportunity using Liang–Kleeman information flow (Liang, 2013). This study demonstrates the ability to identify sources of cross-scale predictability by using complex continuous wavelet transform and an information-theoretic approach to causality (Paluš, 2014).