Labrador Sea subsurface density as a precursor of multidecadal variability in the North Atlantic: a multi-model study

The subpolar North Atlantic (SPNA) is a region with prominent decadal variability that has experienced remarkable warming and cooling trends in the last few decades. These observed trends have been preceded by slow-paced increases and decreases in the Labrador Sea density (LSD), which are thought to be a precursor of large-scale ocean circulation changes. This article analyses the interrelationships between the LSD and the wider North Atlantic across an ensemble of coupled climate model simulations. In particular, it analyses the link between subsurface density and the deep boundary density, the Atlantic Meridional Overturning Circulation (AMOC), the subpolar gyre (SPG) circulation, and the upper-ocean temperature in the eastern SPNA.

All simulations exhibit considerable multidecadal variability in the LSD and the ocean circulation indices, which are found to be interrelated. LSD is strongly linked to the strength of the subpolar AMOC and gyre circulation, and it is also linked to the subtropical AMOC, although the strength of this relationship is model-dependent and affected by the inclusion of the Ekman component. The connectivity of LSD with the subtropics is found to be sensitive to different model features, including the mean density stratification in the Labrador Sea, the strength and depth of the AMOC, and the depth at which the LSD propagates southward along the western boundary. Several of these quantities can also be computed from observations, and comparison with these observation-based quantities suggests that models representing a weaker link to the subtropical AMOC might be more realistic.

1 Introduction

The North Atlantic Ocean is a key component in Earth's climate through, for example, its role in redistributing heat and in taking up excess heat and carbon from the atmosphere. It is also a region that has varied significantly in the past. This is particularly true for the North Atlantic subpolar gyre, which has varied significantly on multidecadal timescales across a range of different variables (Häkkinen and Rhines, 2004; Holliday et al., 2020; Reverdin, 2010; Robson et al., 2018b). Basin-mean sea surface temperature (SST) over the North Atlantic has also been observed to vary on multidecadal timescales (Schlesinger and Ramankutty, 1994) and has been linked to a range of important climate impacts, including hurricane numbers and rainfall in monsoon regions (Knight et al., 2006; Monerie et al., 2019; Zhang and Delworth, 2006). The North Atlantic is also expected to change significantly in the future due to the effects of climate change and consequently produce substantial climate impacts on the surrounding regions (Sutton and Hodson, 2005; Woollings et al., 2012). On decadal timescales, it is the interaction between natural variability and externally forced changes that will shape how the Atlantic region's climate will evolve. Therefore, in order to improve predictions of the North Atlantic, it is imperative that we improve our understanding of the processes that control decadal-timescale changes in this region.

It has generally been thought that changes in the ocean circulation, particularly the Atlantic Meridional Overturning Circulation (AMOC), have played a significant role in shaping the Atlantic multidecadal variability (AMV; Knight et al., 2005). In particular, changes in the strength of the AMOC and its related ocean heat transports have been shown to control multidecadal internal variability in a range of coupled climate models (Danabasoglu, 2008; Dong and Sutton, 2005; Jungclaus et al., 2005; Ortega et al., 2011, 2015). The proposed mechanisms to explain the multidecadal variability involve interplays between the North Atlantic Oscillation (NAO), North Atlantic Deep Water (NADW) formation, the boundary currents, the Gulf Stream and gyre circulations, and the horizontal density gradients (e.g. Joyce and Zhang, 2010; Polyakov et al., 2010; Ba et al., 2013; Nigam et al., 2018; Zhang et al., 2019). Changes in the AMOC and the wider ocean circulation have indeed been used to explain the observed changes in the subpolar North Atlantic (SPNA) on decadal and longer timescales (Moat et al., 2019). In particular, the SPNA underwent a rapid warming and salinification in the mid-1990s before a decadal-timescale cooling and freshening started in 2005, which is consistent with decadal to multidecadal variability of the AMOC (Robson et al., 2012, 2013, 2016). The recent cooling has been linked to climate impacts over the continents, including heat waves (Duchez et al., 2016), through an effect on the position of the jet stream (Josey et al., 2018). A long-term relative cooling of the SPNA since ∼ 1850 has also been attributed to a centennial weakening of the AMOC (Caesar et al., 2018; Rahmstorf et al., 2015), an AMOC reduction that most CMIP6 model projections predict to continue in the future (Weijer et al., 2020). However, a lack of direct observations of the strength of the AMOC and the ocean circulation more generally have hindered our ability to make a direct attribution of recent changes.

In order to understand the aforementioned changes in the SPNA on multidecadal timescales many authors have turned to indirect measurements of the AMOC. One particular proxy for AMOC strength that has received some focus recently involves density anomalies at depth in the western SPNA or Labrador Sea region. In climate models, density anomalies in the western SPNA are a key predictor of density anomalies further south on the western boundary and hence of the AMOC strength via thermal wind balance (Hodson and Sutton, 2012; Ortega et al., 2017; Robson et al., 2014, 2016). Observations show considerable decadal variability in subsurface density anomalies; density anomalies in the western SPNA and Labrador Sea between ∼ 1000 and 2500 m increased significantly, peaked in ∼ 1995, and subsequently declined (Robson et al., 2016; Yashayaev and Loder, 2016). Therefore, these density anomalies have been interpreted as indicating that the AMOC peaked in the middle to late 1990s and then declined, consistent with the warming and then cooling of the eastern SPNA (Hermanson et al., 2014; Ortega et al., 2017; Robson et al., 2016). Time series of subsurface density anomalies in the western SPNA are also consistent with other proxies for AMOC strength, including sea-level-based proxies (McCarthy et al., 2015; Sutton et al., 2018), sediment based proxies (Thornalley et al., 2018), and upper-ocean heat content fingerprints (Caesar et al., 2018; Zhang, 2008). Furthermore, the decline in the AMOC suggested by the above proxies is also consistent with the observed AMOC decline at 26^∘  N since 2004 (Smeed et al., 2018) and with the changes in the AMOC seen in ocean data assimilation systems (Jackson et al., 2016, 2019). Therefore, there is confidence that large-scale changes in North Atlantic Ocean circulation have occurred over the past few decades and that they have had a significant impact on upper-ocean heat content.

Although there is consistency across proxies for AMOC changes in the North Atlantic, there are considerable gaps in our understanding and major uncertainties to overcome. For example, the development of subsurface density proxies has been investigated so far with just a few models (Ortega et al., 2017; Robson et al., 2014). However, there is considerable spread across climate models in the simulations of AMOC mean state and variability (Reintges et al., 2017; Zhang and Wang, 2013) and also in the latitudinal coherence of AMOC anomalies (Li et al., 2019; Roberts et al., 2020; Hirschi et al., 2020), which might reflect different roles of deep density anomalies in the western SPNA for the AMOC, as well as different interplays between the subpolar and subtropical gyre contributions (Zou et al., 2020). Models also do not realistically resolve many key features of the AMOC, most notably the overflows, and this affects the subsurface stratification downstream and on the western boundary (Zhang et al., 2011). Significant uncertainty also remains for other important processes. For example, it is not yet clear whether the recent changes in the SPNA are an ocean response to buoyancy forcing or whether mechanical wind forcing has shaped the recent observed changes (Robson et al, 2016; Piecuch et al., 2017). Local surface fluxes are also likely to explain a significant proportion of the recent cooling (Josey et al, 2018). Subsurface density anomalies are not just a proxy for the AMOC, but also more generally for buoyancy-forced (or thermohaline) circulation changes, including gyre changes (Ortega et al., 2017; Yeager, 2015). Finally, the AMOC variability is also thought to respond to local wind forcing on a range of timescales, especially at lower latitudes (Polo et al., 2014; Zhao and Johns, 2014), which could disrupt or “mask” the influence of subsurface density anomalies as they propagate further south.

There is also considerable uncertainty in how and where subsurface density anomalies are formed in the SPNA and how they are related to the AMOC. In observations and models, most water transformation associated with the AMOC occurs within the SPNA, particularly in the eastern SPNA (Desbruyères et al., 2019; Grist et al., 2014; Langehaug et al., 2012). However, decadal changes in subsurface density anomalies in the western SPNA have often been linked to buoyancy forcing and changes in deep convection in the Labrador Sea or to changes in the volume of Labrador Sea Water production (Yashayaev and Loder, 2016; Yeager and Danabasoglu, 2014). Many studies have also reported that the basin-wide AMOC in ocean-only and coupled models is sensitive to heat flux or buoyancy forcing in the Labrador Sea (Kim et al., 2020; Ortega et al., 2011, 2017; Xu et al., 2019; Yeager and Danabasoglu, 2014). Indeed, idealized experiments have shown that persisting positive NAO phases can strengthen the AMOC by fostering deepwater formation via increased surface cooling in the Labrador Sea, thus inducing changes in the zonal density gradient (Delworth and Zeng, 2016; Kim et al., 2020) and thermal wind responses. However, the real link between deep convection, deepwater formation, and density anomalies at depth in the Labrador Sea is complex and not fully understood (Katsman et al., 2018). Observations suggest that very little water transformation and deepwater formation actually occur in the Labrador Sea (Pickart and Spall 2007; Lozier et al., 2019). Indeed, recently it has been shown that the Labrador Sea (i.e. OSNAP west) has played a very minor role in the interannual variability observed so far across the whole OSNAP line (Lozier et al., 2019), with the Irminger Sea playing a more dominant role. The Irminger Sea is a region that in some models controls the AMOC and SPNA variability and that is especially sensitive to advective processes (Ba et al., 2013) and Arctic overflows (Fröb et al., 2016). Moreover, ocean-only models appear to significantly overestimate the amount of deep water formed within the Labrador Sea, with likely implications for coupled models (Li et al., 2019). These inconsistencies raise the question of whether models are simulating the right relationships.

In this study we will address some of the above uncertainties by performing a multi-model analysis of the North Atlantic in coupled climate models. We focus on the question of how robust the relationship is between subsurface Labrador Sea density anomalies and the basin-wide Atlantic Ocean circulation on decadal timescales. We also address the question of whether Labrador Sea density can robustly induce density changes over the western continental slope and generate a geostrophic response in the meridional circulation (Bingham and Hughes, 2009; Roussenov et al., 2008). Shedding new light on these links is important to, among other reasons, determine to what extent the RAPID measurements represent the variability of the basin-wide AMOC cell and to identify the models that can produce more reliable predictions and projections of the SPNA. For this, we will specifically assess the connection between subsurface density and AMOC at high and low latitudes via the western boundary. Furthermore, we will determine whether models consistently support an impact of AMOC changes on the SPNA upper-ocean temperatures and, if not, investigate why. Our primary aim is to provide, for the first time in a multi-model context, a broad characterization of these relationships using consistent analysis frameworks and tools, documenting the uncertainty. The reasons for the uncertainty in the relationships will also be explored, establishing links to key model climatological properties that could eventually be exploited as emergent constraints. We intentionally do not explore in detail how subsurface density anomalies are formed in these models and leave this for further study.

The paper is organized as follows. Section 2 describes the experiments and methods. Labrador Sea density and its link to the ocean circulation and the wider North Atlantic are explored across the multi-model ensemble in Sect. 3. The characteristics of the intermodel spread in the previous relationships are explored in Sect. 4. Section 5 presents the main conclusions of this study and discusses its implications.

2 Experiments and methods

Here we provide an overview and brief description of the models used in this study and provide some statistical considerations for the intermodel comparison.

2.1 Experiment selection

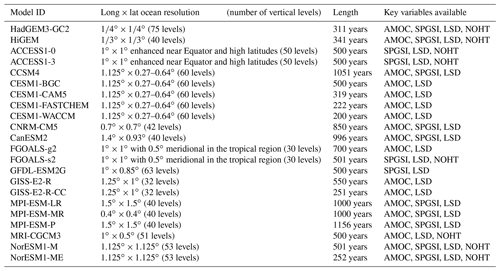
For the multi-model analysis, we use the preindustrial control simulations (picontrol) from the fifth phase of the Coupled Model Intercomparison Project (CMIP5; Taylor et al., 2012), in which forcing values of greenhouse gases (GHGs), aerosols, ozone, and solar irradiance are fixed to 1850 levels. We chose to use control over historical simulations to focus exclusively on internal variability and benefit from the more robust statistics that the long preindustrial experiments provide. Furthermore, we avoid the forced trends present in the historical experiments, which can lead to correlations that are difficult to interpret objectively (Tandon and Kushner, 2015). From the CMIP5 ensemble, we only use models in which 3D fields of ocean temperature and salinity, as well as the streamfunctions of meridional overturning circulation and/or the barotropic circulation, were available. A total of 20 different models meet this condition. Their main characteristics and number of simulation years have been summarized in Table 1. Most of the models have a nominal horizontal resolution in the ocean close to 1^∘ and therefore cannot resolve the effects of eddies. Menary et al. (2015) have shown for these same model simulations that the effective horizontal resolution can be higher over the Labrador Sea due to the non-regular grids. Effective resolutions over the Labrador Sea area range from 0.21^∘ in the GC2 model to 1.1^∘ in GISS-E2-R, GISS-E2-R-CC, and CanESM2, with these differences determining to a large extent the mean state model biases and the dominant drivers (i.e. salinity or temperature) of the Labrador Sea density changes.

Complementing these simulations, we also consider two control experiments with eddy-permitting resolutions. Specifically, we use a present-day control simulation (i.e. with fixed radiative forcing levels from the year 1990) of the HiGEM model, with a nominal horizontal resolution in the ocean of $\mathrm{1}/\mathrm{3}$^∘ and of 0.83^∘ latitude × 1.25^∘ longitude in the atmosphere (Shaffrey et al., 2009), and a preindustrial control of HadGEM3-GC2 (hereafter, GC2; Ortega et al., 2017) with a nominal resolution in the ocean of $\mathrm{1}/\mathrm{4}$^∘ (ORCA025) and N216 in the atmosphere (i.e. approximately 60 km in the mid-latitudes). The GC2 simulation is the same one employed for previous analyses of Labrador Sea variability in Robson et al. (2016) and Ortega et al. (2017). Note that we will assume that the present-day control in HiGEM can be compared with the other preindustrial simulations due to the large uncertainty the latter show in their climatological biases; so, for the sake of simplicity, we will only refer to preindustrial control experiments from now on. Figure 1 demonstrates that this assumption is reasonable, since the mean Labrador Sea stratification in HiGEM is very similar to that in the other models.

As an observationally constrained reference, this study also includes the assimilation run from DePreSys3, a decadal prediction system from the Met Office based on GC2 (Dunstone et al., 2016). In the ocean, the assimilation is performed through a strong nudging (10 d relaxation timescale) towards the full fields of a three-dimensional objective temperature and salinity analysis (Smith and Murphy, 2007). Since it covers a comparatively shorter period (1960–2013) and therefore different timescales than the control experiments, its comparison with the other simulations will be done with caution, in particular regarding the indices of the large-scale Atlantic circulation, for which other assimilation products show important discrepancies (Karspeck et al., 2015), thus highlighting significant uncertainty. For evaluation purposes, we also use EN4.2.1 (Good et al., 2013), an objective analysis of monthly temperature and salinity 3D observations developed at the Met Office.

Table 1 List of the models used for this study, their characteristics, and those of their picontrol simulations. For further details on the CMIP5 model configurations and components, please refer to Table 9A1 in Flato et al. (2013) and references therein.

2.2 Methodological considerations

Density values are computed from 3D salinity and potential temperature fields using the International Equation of State of Seawater (EOS-80) and are referenced to the level of 2000 dbar (σ₂) to give stronger emphasis to the deepwater properties.

Statistical significance of correlation coefficients is assessed following a two-tailed Student's t test that takes into account the series' autocorrelation to correct the sample size, reducing the degrees of freedom of a series to its effective value (Bretherton et al., 1999).

Because our goal is to provide further insight into the suggested relationships established from observed trends in the North Atlantic (e.g. Robson et al., 2016), all statistical analyses in this study exploring the relationships between variables and associated lags are based on 10-year running trends. This is analogous to the calculation of a typical 10-year running mean, but computing a linear trend instead over each 10-year period and keeping the slope value. Note also that our main results remain similar if decadal running means are applied instead (not shown), as both are alternative approaches to concentrate on the low-frequency variability. Running trends also have the particular advantage of not being sensitive to long-term drifts, which are still present (and can be important for some simulations and variables) when running means are computed. To illustrate how decadal running trends represent low-frequency variability and how they compare with the decadal running means, both have been included in Fig. 2b (solid thick lines vs. dashed thin lines) for an index of Labrador Sea density.

3 Labrador Sea density as an index of multidecadal North Atlantic variability

This section explores the potential of Labrador Sea density as a proxy for the ocean circulation changes in the North Atlantic. As in our previous studies (Ortega et al., 2017; Robson et al., 2016), the indices that we will define herein represent waters within the Labrador Sea and not those that are necessarily formed in the region (e.g. Labrador Sea Water). Since Labrador Sea variability is affected by different processes (e.g. vertical mixing, Arctic–Atlantic overflows, sea ice interactions) that can be represented differently in the models in both time and space, we characterize its variability over a relatively broad box (60–35^∘ W, 50–65^∘ N; blue box in Fig. 1a) that also includes part of the Irminger Sea region. Note that over this large area, EN4.2.1 shows the weakest density stratification in the North Atlantic (characterized in Fig. 1a as the density difference between 1000 m and the surface).

3.1 Labrador Sea density across models

A first indicator of potential model discrepancies is Labrador Sea stratification, which can lead to differences in the representation of deep ocean convection (i.e. weaker density stratifications will facilitate mixing, fostering convection activity, and vice versa for stronger density stratifications). Figure 1b–d illustrate the intermodel differences with the vertical profile of the spatially averaged Labrador Sea temperature, salinity, and density. The largest discrepancies are seen for temperature. Most models present their warmest waters at the surface, and temperatures decrease sharply to minimum values around 100 m and increase again at deeper levels, reaching uniform conditions after approx 300 m. However, the location and magnitude of this temperature minimum and the two maxima are highly variable. It is important to note that the profile for one of the models, MRI-CGCM3, is noticeably different to the others, with a subsurface minimum more than 2^∘ colder than for any other model. In terms of salinity, the general profile is more coherent across models, with minimum salinity at the surface that progressively increases with depth and attains uniform values after 500 m. Density stratification seems to be determined by salinity, as their two vertical profiles show similar features. This similarity includes exceptionally strong density and salinity stratification in MRI-CGCM3 compared with the other models. This stratification is so strong that it precludes the occurrence of deep convection (not shown). Because of this, MRI-CGCM3 is an outlier for many of the metrics used in the paper and has been excluded from the subsequent analyses to facilitate the interpretation of our results. We also note that the profiles for the two eddy-permitting models (green and orange lines in Fig. 1b, d) lie within the spread of the CMIP5 models, indicating that resolution (at least to eddy-permitting spatial scales) does not drastically change stratification in the region. The DePreSys3 assimilation run closely matches the stratification in EN4.2.1, which supports the DePreSys assimilation run as a reasonable observation-constrained reference for the models. The comparison of both observation-based datasets with the rest of simulations suggests that, in the subsurface, all models are too warm and most of them are too salty; these two biases have a competing effect on the mean subsurface density. Because of these cancelling effects, several models show a comparatively better representation of the subsurface densities when compared to EN4.2.1 and DePreSys3. This compensation of model shortcomings for temperature and salinity is clearly illustrated in HiGEM, which shows remarkable agreement with EN4.2.1 below 500 m.

To represent the characteristic interannual variability of Labrador Sea densities (hereafter referred to as LSD for consistency with previous work), we perform an empirical orthogonal function (EOF; Storch and Zwiers, 1999) analysis and extract the leading mode for the spatially averaged annual means of LSD (Fig. 2a), as in Ortega et al. (2017). For all simulations the first EOF of LSD exhibits a vertical structure with density values that are largest at or near the surface and gradually decrease with depth. Thus, this first EOF typically reflects situations in which the density stratification, as described by the climatological vertical profile in Fig. 1d, is weakened or strengthened, which happens when the corresponding principal component takes positive and negative values, respectively. Some intermodel discrepancies are evident, in particular regarding the depths at which the maximum density values are found, which can happen between the surface and 500 m. Despite these differences, the dominant timescales of LSD variability seem to coincide between models. For example, Fig. 2b illustrates the first principal component of LSD (PC1-LSD) for GC2 and HiGEM, showing clear multidecadal variability in both cases. Furthermore, Fig. 2c shows the Fourier spectrum analysis of the annual PC1-LSD values, and most models show enhanced PC1-LSD variability for periodicities between 5 and 30 years.

In addition to the PC1-LSD index we consider a deep LSD index as introduced in Robson et al. (2016). The deep LSD index is defined as the 1000–2500 m vertical mean of the spatially averaged density over the same region as PC1-LSD. We now compare how both indices represent the low-frequency changes in LSD, which are described in this paper as decadal running trends. A lead–lag correlation between the decadal trends in both PC1-LSD and deep LSD indices shows that they are strongly correlated in all models. However, some differences emerge when considering the lag of maximum correlation (Fig. 2d). This comparison might indicate, once again, that decadal variability of subsurface density is concentrated at different depths in different models. It is also possible that both indices are sensitive to changes in deepwater formation in different locations (e.g. Irminger or GIN seas), which could hence affect the depth and maximum lag of the correlations. Nevertheless, we adopt PC1-LSD for the rest of the analyses, as it has the advantage of adjusting in each model to the depths at which density variability is more prominent.

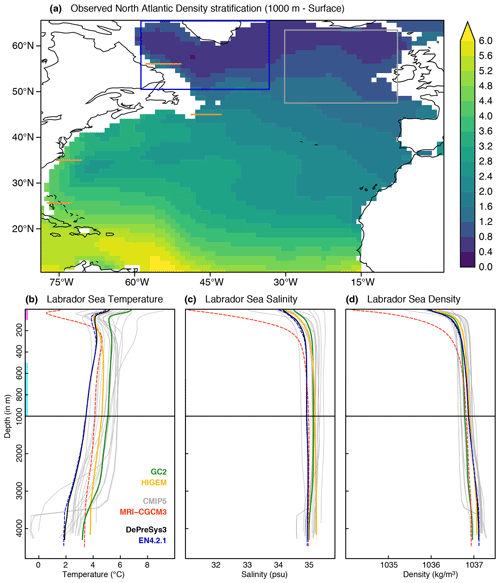
Figure 1 (a) Climatological density (computed as σ₂ at all depth levels) difference between the subsurface (1000 m) and surface in the North Atlantic in the observational dataset EN4.2.1 (Good et al., 2013). The reference period to compute the climatology is 1960–2013. The grey box (32–10^∘ W and 47–63^∘ N) encloses the region where the ESPNA-T700 index in Fig. 4d is computed. (b–d) Climatological mean of the spatially averaged Labrador Sea (60–35^∘ W, 50–65^∘ N; blue box in a) temperature, salinity, and density as a function of depth in the simulation ensemble, the DePreSys3 assimilation run, and EN4.2.1. The magenta (cyan) bars on the vertical axis correspond to the depths that have been used to define the vertical stratification Labrador Sea indices. The horizontal orange lines by the North American coast represent the location of the latitudinal cross sections in Figs. 10 and 11. For each model and dataset the climatology is computed for its whole length except for EN4.2.1, which is computed for the overlap period with the DePreSys3 assimilation run.

Figure 2 (a) First empirical orthogonal function (EOF) as a function of depth of the spatially averaged LSD in all the preindustrial experiments and in the DePreSys3 assimilation run. The percentage of variance explained by this mode in each model is included in brackets in the legend (for the CMIP5 runs, this represents the mean value across the ensemble). Because the sign of an EOF is arbitrary, it has been adjusted for all models (together with the sign of the respective principal component) so that both represent an increase in density stratification. (b) Associated principal component of the spatially averaged LSD (PC1-LSD) in the two high-resolution experiments. The thin solid lines represent the raw yearly resolved PC1-LSD time series, the thin dashed lines their respective 10-year running means, and the thick (and slightly darker) lines their associated 10-year running trends (centred around the last year of the decade over which the trend is computed). (c) Normalized Fourier spectra of the PC1-LSD index in each of the preindustrial simulations. The black thick line represents a red noise process with the same first autoregressive (AR1) coefficient as PC1-LSD in GC2, and the dashed line sets the 95 % confidence interval of this red noise process. No major differences are found when using HiGEM's AR1 coefficient instead. The red vertical line highlights the 10-year periodicity to separate the interannual from the decadal to multidecadal timescales. (d) Lead–lag correlations between the decadal trends in PC1-LSD and those in the deep LSD index from Robson et al. (2016), defined as the 1000–2500 m average density in the box 60–35^∘ W, 50–65^∘ N. Positive lags indicate that PC1-LSD leads the changes in deep LSD. Full dots denote correlation values exceeding a 95 % confidence level based on a Student's t test that takes into account the series autocorrelation.

3.2 Labrador Sea density linkages to the ocean circulation

The link between PC1-LSD and other ocean circulation indices in the North Atlantic is now examined. Three indices are considered: the AMOC at two different latitudes of 26^∘ N (i.e. the same latitude as the RAPID array) and 45^∘ N to capture the typical variability of the subpolar AMOC and an index of the subpolar gyre strength. The AMOC indices are computed as the maximum of the North Atlantic overturning circulation at any depth. Furthermore, the Ekman component is removed to focus on the slow wind-forced and the thermohaline-driven (i.e. the only one that can be influenced by the PC1-LSD directly) AMOC changes. To compute the Ekman component, we vertically integrate the Ekman velocities (after introducing a depth-uniform return flow to ensure no net meridional mass transport) following Eq. (6) in Baehr et al. (2004) with a fixed Ekman layer depth of 50 m. This Ekman component is then removed at each depth level, prior to the calculation of the AMOC indices. The subpolar gyre strength is computed as an average of the North Atlantic barotropic streamfunction in the Labrador Sea region (60–35^∘ W, 50–65^∘ N), where the gyre strength is usually maximum. Since the SPG circulation is cyclonic and therefore associated with negative barotropic streamfunction values, the subpolar gyre strength index (SPGSI) is multiplied by −1 so that an intensification of the gyre corresponds to a positive value of the index. The Fourier spectra of the raw ocean circulation indices (Fig. 3) show that, similar to the PC1-LSD, all three indices have strong multidecadal variability, with the largest differences with respect to PC1-LSD emerging for timescales between 10 and 30 years, for which the spectral power is comparatively weaker. Important differences are also seen at 50-year and longer timescales, for which the ocean circulation indices appear to have enhanced variability with respect to PC1-LSD. Similar spectra, but with enhanced variance at short timescales and reduced variance at the longest timescales, are obtained for the AMOC indices when the Ekman component is kept (Supplement Fig. S1), which suggests that the low-frequency processes dominate the total AMOC variability.

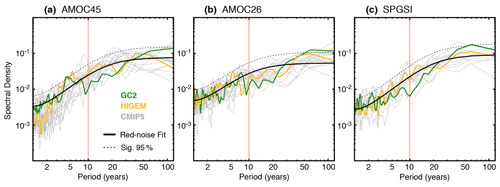
Figure 3 (a–c) Fourier spectra in the picontrol ensemble for the indices AMOC45, AMOC26, and SPGSI. Red noise spectra corresponding to a first-order autoregressive process fit to GC2 indices are provided as a reference.

Figure 4a shows that decadal trends in PC1-LSD are associated with trends in the AMOC at 45^∘ N (AMOC45). Nevertheless, there is some intermodel spread regarding the lag of maximum correlation, which ranges between 0 and 2 years (with PC1-LSD leading), although both variables are in phase for the majority of models. The AMOC at 26^∘ N (AMOC26) is also positively related to PC1-LSD, with PC1-LSD leading AMOC26 by 3 years on average (Fig. 4b). However, the average correlation between PC1-LSD and AMOC26 is weaker, and the spread in the magnitude and lag of the maximum correlation is larger than for AMOC45. Therefore, it appears that the link to the subtropics is weaker than for 45^∘ N and that AMOC coherence between subpolar latitudes and the subtropics in coupled models is model-dependent. This weaker link of PC1-LSD to the subtropical AMOC is not surprising, as the LSD anomalies need to propagate over a longer distance along the western boundary, allowing model differences in the representation of ocean currents and gyres to impact the timing and magnitude of the maximum correlations. The reasons for the spread in the relationship between PC1-LSD and AMOC26 are explored in Sect. 4. A strong relationship is also found between PC1-LSD trends and those in SPGSI (Fig. 4c), which are of similar order as for AMOC45. Thus, overall, PC1-LSD is a good proxy for the large-scale ocean circulation in the subpolar North Atlantic and can also be a precursor for a fraction of the AMOC variability in the subtropical Atlantic.

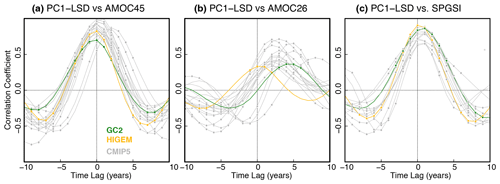
Figure 4 (a) Lead–lag correlations across the picontrol ensemble between the PC1-LSD index and the maximum AMOC streamfunction at 45^∘ N after the Ekman transport is removed (AMOC45). Correlations are based on 10-year running trends. Significance is assessed as in Fig. 2d and is indicated with a circle. For positive lags, PC1-LSD leads. (b–c) The same as in (a) but between PC1-LSD and the maximum AMOC streamfunction at 26^∘ N after the Ekman transport is removed (AMOC26) and the subpolar gyre strength index (SPGSI).

PC1-LSD is also a good precursor of the full AMOC variability (i.e. including the Ekman transport), although the wind-induced fluctuations associated with the Ekman component can introduce differences in the lags of the maximum AMOC vs. PC1-LSD correlations (Supplement Fig. S2). This different lag can be explained by the fact that when the Ekman component is included, the AMOC contains a signal that is instantaneously driven by basin-scale surface wind anomalies (such as those driven by the NAO) that are, ultimately, also linked to the heat loss in the subpolar North Atlantic, which induces a delayed influence on the PC1-LSD (Ortega et al., 2017). Hence, including Ekman can lead to counterintuitive relationships in some models, in which the AMOC appears to lead the PC1-LSD changes. Also, in the particular case of GC2, the interference of the two signals (i.e. the subtropical Ekman and the delayed PC1-LSD) renders the correlations in Supplement Fig. S2d insignificant, masking out the real influence of PC1-LSD on the subtropics. For those reasons and to ease the interpretation of the lagged relationships, the rest of the analysis is exclusively focused on the AMOC indices without Ekman.

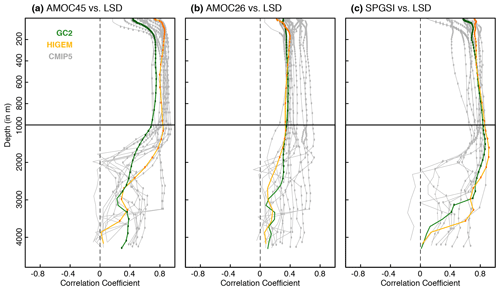
Figure 5 (a) Maximum correlation (for any lag between 0 and 10 years) between the AMOC45 index (after the Ekman transport is removed) and Labrador Sea densities as a function of depth for all the simulations. Coloured dots indicate correlations that are significant at the 95 % confidence level. (b–c) The same as in (a) but between the AMOC26 index and LSD and between the SPGSI and LSD, respectively.

The role of PC1-LSD as a precursor of the AMOC is further supported by a parallel analysis in Fig. 5, looking at the maximum correlation between the decadal AMOC trends and those in Labrador Sea density as a function of depth, with the latter leading the AMOC by up to 10 years. Figure 5 reveals that the strongest link between the Labrador Sea densities and the AMOC, both at 45 and 26^∘ N, occurs in its first 1000 m, the same levels at which the first EOF of LSD shows the maximum loadings (Fig. 2a), which confirms the appropriateness of using PC1-LSD to represent the ocean circulation. The same analysis also supports a strong link between SPGSI and LSD, although in that case the largest correlations usually happen at deeper levels (between 1000 and 2000 m). Note that the main conclusions drawn from PC1-LSD are also valid for the deep LSD index; however, the intermodel differences are larger in the cross-correlations with the AMOC indices (Supplement Fig. S3). This difference could reflect the fact that the deep LSD index is more sensitive to other influences, like the Arctic overflows (Ortega et al., 2017), which can be very differently represented across models. Overall, the PC1-LSD index seems to be a better choice to describe multidecadal North Atlantic variability in multi-model comparisons, as it selects the key depths for each model. However, PC1-LSD is mostly focused on near-surface levels and therefore likely represents mostly Labrador Sea forced variability. Other indices describing densities at deeper levels might be preferable to compare Labrador Sea Water of different origins across models and to evaluate its realism against observations.

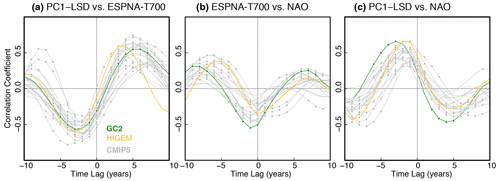
Figure 6 (a) Lead–lag correlations across the picontrol ensemble between the PC1-LSD index and the vertically averaged top 700 m temperatures in the eastern subpolar gyre (ESPNA-T700; grey box in Fig. 1a). Correlations are based on 10-year running trends. Significance is assessed as in Fig. 2d and is indicated with a circle. For positive lags, PC1-LSD leads. (b–c) The same as in (a) but between the North Atlantic Oscillation (NAO; defined as the standardized difference in sea level pressure between the closest grid points to Azores and Reykjavik) and the ESPNA-T700 and between the NAO and the PC1-LSD, respectively. In these two cases, for negative lags the NAO leads.

3.3 Labrador Sea density linkages to the wider North Atlantic

Previous studies based on the GC2 picontrol simulation have suggested LSD to also be a potential predictor of widespread cooling events in the eastern SPNA, like the observed cooling over 2005 to 2014 (Robson et al., 2016; Ortega et al., 2017). We therefore continue our exploration of the PC1-LSD index by investigating its link to the eastern SPNA in the multi-model ensemble. To explore this link we introduce a new index that represents the mean potential temperature in the eastern SPNA region (32–10^∘ W, 47–63^∘ N) averaged over the top 700 m of the ocean (ESPNA-T700). Lead–lag correlations between the decadal trends in PC1-LSD and this index (Fig. 6a) show that there is a coherent relationship between the two variables across models, with PC1-LSD increases (decreases) being consistently followed by ESPNA-T700 warmings (coolings). Nevertheless, there are intermodel differences concerning the magnitude and lag of the strongest positive correlations, revealing important uncertainty in the relationship. The spread in the PC1-LSD vs. ESPNA-T700 relationship is thus reminiscent of the spread found between PC1-LSD and AMOC26, which suggests that they might be related. We also note significant negative correlations when ESPNA-T700 leads PC1-LSD by 2–4 years that might be explained by the opposing (and nearly concomitant) impacts that the NAO exerts on both variables (Fig. 6b, c). Positive NAO phases and associated surface buoyancy forcing (Lozier et al., 2008) lead in first instance to negative SSTs (Barrier et al., 2014; Lohmann et al., 2009) and an almost simultaneous cooling in ESPNA-T700 (Fig. 6b). In comparison, on the western side of the SPNA, positive NAO phases contribute to reduce vertical density stratification, favouring convection and a more positive LSD index (Robson et al., 2016), which in the models lags the NAO by 2–3 years (Fig. 6c). The fact that correlations between NAO and ESPNA-T700 are weaker than between PC1-LSD and ESPNA-T700 suggests that the ocean might also be playing an additional role (besides the NAO) in controlling the ESPNA temperatures.

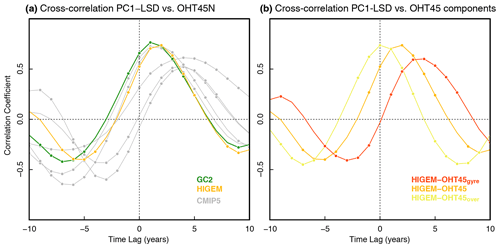
Figure 7 (a) Lead–lag correlations in a subset of the picontrol experiments between the PC1-LSD index and the ocean heat transport across the 45^∘ N transect (OHT45N). Note that the ocean heat content is only available for five models of the CMIP5 ensemble. Correlations are based on 10-year running trends. (b) The same as in (a) but only in HiGEM for the different terms of the OHT45N. For positive lags, PC1-LSD leads.

The link between PC1-LSD and the ESPNA could be explained through an influence of the PC1-LSD on the meridional ocean heat transport. This link is now investigated in two eddy-permitting simulations (Fig. 7) and five CMIP5 models for which the ocean heat transport fields are publicly available. In the two high-resolution experiments and two of the CMIP5 ones the decadal trends in the meridional ocean heat transport at 45^∘ N (OHT45) are strongly linked to those in PC1-LSD. This is a similar relationship to the one previously found in Fig. 4 between PC1-LSD and both the AMOC45 and SPGSI, but in this case with PC1-LSD leading with a slightly longer lead time. The other CMIP5 experiments support a weaker, yet significant, link and a longer lag between OHT45 and PC1-LSD. Altogether, Fig. 7a confirms that PC1-LSD is a good precursor of the changes in the meridional ocean heat transport, although with some differences across models which might reflect a different representation of certain processes. The contributions of two different processes to this delay are further investigated in HiGEM, for which OHT was decomposed online at each time step into vertical and horizontal heat transports (as in Bryan, 1969) that can be respectively interpreted as the “overturning” (i.e. characterized by the zonal mean transport) and “gyre” (i.e. characterized by variations from the zonal mean transport) components (Robson et al., 2018a). While the overturning contribution (OHT45_over) increases in phase with the AMOC45, SPGSI, and PC1-LSD changes (Fig. 7b), the increase in the gyre component (OHC_gyre) starts 4 years later. That lag could be the time required in HiGEM for the propagation of mean and/or anomalous temperatures from the southern to the northern branch of the SPG.

4 Characteristics of the intermodel spread in the subpolar to subtropical AMOC

This section investigates which particular climatological model features are linked to the large intermodel spread in the PC1-LSD vs. AMOC26 relationships. The most relevant model features thus identified will improve our process understanding and can eventually be used to identify which models are most realistic and, in turn, can deliver more reliable projections of the future changes in the North Atlantic.

Figure 8 shows that models that simulate a stronger and deeper climatological AMOC (both at 45 and 26^∘ N) tend to have a stronger correlation between PC1-LSD and the subtropics. All these linear relationships between climatological AMOC strength and depth as well as the PC1-LSD vs. AMOC26 connectivity are significant at the 95 % confidence level. These climatological AMOC values (without Ekman) can be put in context with those from RAPID observations and DePreSys3. RAPID observational uncertainties have been considered by including the mean values over three different non-overlapping periods (i.e. 2004–2007, 2008–2012, and 2013–2016; dotted lines in Fig. 8). The scatterplots show that the majority of models whose climatological AMOC26 lies within the RAPID/DePreSys3 climatological spread have a relatively weak link between PC1-LSD and AMOC26, although some models supporting a strong link are also included or remain close to the RAPID/DePreSys3 values. However, caution is recommended before defining emerging constraints because models and observations are not directly comparable for numerous reasons. For example, both RAPID and DePreSys3 cover shorter periods than the simulations and relate to different background forcing conditions (present day vs. preindustrial), which might imply different mean states (Thornalley et al., 2018). Also, climatological values of the AMOC26 strength are notably weaker in DePreSys3 than in RAPID, a difference that is not explained by the different temporal periods covered by each dataset (not shown) and that implies that DePreSys3 might also be underestimating the real AMOC45 strength. This underestimation could be larger than shown in Fig. 8, as evidence suggests that RAPID calculations from mooring arrays might be underestimating the AMOC strength by ∼ 1.5 Sv (Sinha et al., 2018).

Figure 8 (a, b) Scatterplot of the maximum cross-correlation value in Fig. 4b between PC1-LSD and AMOC26 against the climatological AMOC45 and AMOC26 means, respectively. All AMOC indices refer to the values after the Ekman transport signal is removed. The maximum correlations are based on 10-year running trends and always happen when PC1-LSD leads the AMOC26 index. Colours indicate the depth at which the climatological AMOC maximum occurs. The correlation coefficient between the maximum PC1-LSD correlation and the climatological mean AMOC is shown in the top left corner in black. The analogous correlation but against the depth of the mean climatological AMOC is shown in magenta. The presence of an asterisk indicates that the correlation is significant at the 95 % confidence level. The dashed grey vertical lines mark the climatological AMOC strength value in the DePreSys3 assimilation run. The orange vertical lines indicate the climatological value from RAPID observations (Smeed et al., 2018) from 2004 to 2016 (dashed) and in three non-overlapping sub-periods of 4 years (dotted).

A potentially important factor behind the intermodel spread in Fig. 4b is the mean density stratification in the Labrador Sea. Figure 9 suggests that, indeed, the PC1-LSD vs. AMOC26 spread is partly influenced by the density stratification in this region. Models that have a weaker density stratification (here defined as the difference between the top 100 m and the average between 500 and 1000 m), and thus favour deeper convection in the Labrador Sea, generally exhibit a stronger link between PC1-LSD and AMOC26. This result is robust for other stratification indices based on different depth levels (See Supplement Fig. S4). Differences in density stratification across models can be due to a combination of different factors, from differences in the local buoyancy fluxes (driven by differences in the atmospheric circulation), to differences in the representation of the Arctic overflows, which are parameterized in some models (e.g. the CESM family; Danabasoglu et al., 2010) and explicitly resolved in others. No robust link between the PC1-LSD vs. AMOC relationship and both temperature and salinity stratification in the Labrador Sea has been found. It is also worth mentioning that all models except CanESM2 are more weakly stratified in the Labrador Sea than the observations (represented herein by the DePreSys3 assimilation run and EN4.2.1). Hence, the real link of LSD to the AMOC26 may not be as strong as some models suggest.

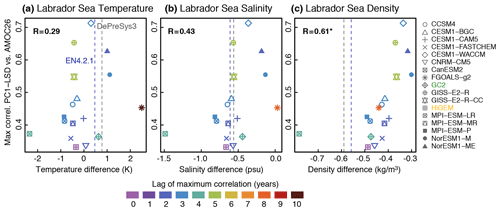
Figure 9 (a) Scatterplot of the maximum cross-correlation value in Fig. 4b between PC1-LSD and AMOC26 (without the Ekman component) against the climatological mean of the Labrador Sea temperature stratification index (computed as the difference of the vertical means in the levels 0–100 m minus the vertical means in the levels 500–1000 m; see Fig. 1). The maximum correlations are based on 10-year running trends. The correlation coefficient between the two metrics is shown in the top left corner. The presence of an asterisk indicates that the correlation is significant at the 95 % confidence level. Colours indicate the lag at which the maximum correlation between PC1-LSD and AMOC26 is obtained. The grey (blue) vertical lines depict the mean stratification value in the DePreSys3 assimilation run (EN4.2.1). In both cases, their overlap period is used to compute the climatology (i.e. 1960–2013). (b–c) The same as in (a) but for the Labrador Sea salinity and density (defined as σ₂), respectively.

Another key aspect of the PC1-LSD vs. AMOC26 connectivity is the western boundary density (WBD). Indeed, boundary density is critical to the mechanism through which LSD influences the AMOC at lower latitudes. Positive (negative) LSD anomalies propagate equatorward following this boundary, and as they do so they strengthen (weaken) the zonal density gradient, triggering a thermal wind response that accelerates (decelerates) the AMOC. In the following we investigate differences in the propagation of boundary densities across models and if these differences can affect the intermodel PC1-LSD vs. AMOC26 spread. Figure 10 focuses on the two high-resolution simulations, wherein important differences already manifest. It represents the in-phase correlations of PC1-LSD with the density fields (defined as σ₂) near the western boundary at four different longitudinal transects: 57 (cutting across the Labrador Sea), 45, 35, and 26^∘ N. In both models, the depth of the maximum correlation near the continental shelf is coherent across latitudes. However, in HiGEM these occur at deeper levels (1000 to 3000 m) compared to GC2 (1000 to 2000 m), and the difference is especially clear at 35^∘ N, where the highest correlations occur at ∼ 2000 m in HiGEM, while they are only at 1000 m in GC2. Similar depth differences are also found at 26^∘ N but with slightly weaker correlations. In addition to the difference in the depth of the maximum correlation between HiGEM and GC2, there are differences in the vertical structure between the two models. For example, at 35^∘ N in GC2, density anomalies on the western boundary form a tripole (low correlation above and below the maximum correlation at ∼ 1000 m), but in HiGEM the density anomalies form a dipole (Fig. 10g). We note some differences in bathymetry at this latitude (which is steeper in HiGEM), which might partly explain some of the differences in terms of the density correlation structure.

Figure 11 shows that the diversity in the depth of these boundary densities is even more evident when including the CMIP5 models. The depth of the maximum correlation between PC1-LSD and the western boundary density at the four latitudinal sections relates linearly (and significantly at the 95 % confidence level) across models to their PC1-LSD vs. AMOC26 correlation. In this case, models exhibiting maximum correlations with the WBDs at deeper levels generally show stronger links between PC1-LSD and the subtropical AMOC. In DePreSys, our observationally constrained reference (dashed grey lines in Fig. 11), these maximum correlations tend to occur at relatively shallow levels when compared with the multi-model ensemble. We have also checked if models with stronger correlations with the WBDs (as represented by the PC1-LSD and WBD maximum correlations at every latitudinal section) also support a stronger link between the PC1-LSD and the AMOC, but this linearity assumption only holds true at 57^∘ N (correlations in magenta in Fig. 11). This suggests that the depth along which WBDs propagate southward and/or the vertical structure of anomalies are the key aspects to understand and potentially narrow down the spread.

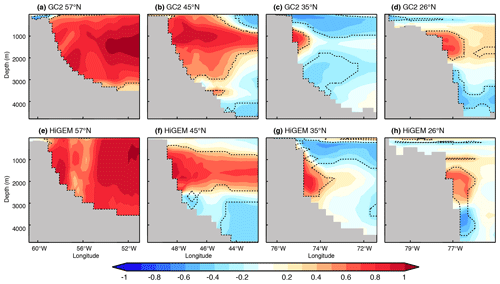
Figure 10 (a) In-phase correlation in GC2 between the PC1-LSD index and the density fields across a zonal section at 57^∘ N located in the vicinity of the western Atlantic boundary. Thin dashed contours enclose areas where the correlation significance exceeds the 95 % confidence level. Correlations are based on 10-year running trends. (b–d) The same as in (a) but for zonal sections at 45, 35, and 26^∘ N. (d–h) The same as in (a–d) but for HiGEM.

5 Conclusions and discussion

This article has explored, in a multi-model context, the linkages between subsurface density in the subpolar North Atlantic (SPNA) and the ocean circulation further south. In particular, it has explored the role of Labrador Sea density (LSD) in driving western boundary density anomalies (WBD) and the ocean circulation, as well as the impact on upper-ocean temperature changes in the SPNA. The analysis was based on two control simulations with eddy-permitting models (a preindustrial one with HadGEM3-GC2 and a present-day one with HiGEM) and on 20 CMIP5 preindustrial experiments. Furthermore, where possible these characteristic model features have been computed in observational datasets and in a simulation assimilating observations. The major findings are listed below.

• All the simulations show clear multidecadal variability in Labrador Sea density. There is also a close link between LSD and the strength of the subpolar Atlantic Ocean circulation, with positive density anomalies leading to a strengthening of the Atlantic Meridional Overturning Circulation (AMOC) at 45^∘ N and the subpolar gyre (SPG) circulation.

• The relationship between anomalous LSD and the strength of the AMOC at 26^∘ N – the latitude of the RAPID array measurements – is also positive in the simulations, but there are significant intermodel differences in both the strength of the relationship and the lag of maximum correlation. This uncertainty implies that the connectivity of LSD to the subtropics and latitudinal AMOC coherence is model-dependent.

• The connectivity between anomalies in LSD and the AMOC at 26^∘ N is sensitive to different model features, including the strength and depth of the climatological AMOC maximum, the mean density stratification in the Labrador Sea, and the depths at which the LSD propagates southward along the western boundary. Stronger LSD connectivity to the subtropics tends to occur in models with a stronger and deeper AMOC, weaker Labrador Sea stratification, and western boundary density propagating at deeper levels.

• Observationally derived constraints of the model-based relationships tend to suggest that the link between LSD and the subtropical AMOC is weak. This suggests that observations of the AMOC via RAPID may not be representative of the basin-wide buoyancy-forced AMOC variability. However, caution is advised because simulations and observations are not directly comparable, so significant uncertainty remains in constraining the relationship between LSD and the subtropical AMOC.

• The multi-model ensemble also supports a significantly lagged relationship between LSD and the upper-ocean temperature in the eastern SPNA, in line with previous studies linking LSD to the recently observed changes in the North Atlantic. However, models disagree regarding the strength of the link (correlations between 0.3–0.7) and the maximum lag (3 to 10 years).

We have shown that, in coupled climate models at least, subsurface density anomalies in the western SPNA are an important predictor of the wider North Atlantic ocean circulation and upper-ocean temperature in the SPNA. This importance for the ocean circulation is especially clear at the latitudes of the SPNA itself. Given the important role of the wind in driving lower-latitude AMOC anomalies and the range of processes through which wind can act on the AMOC (Duchez et al., 2014a, b; Kanzow et al., 2010; Polo et al., 2014; Zhao and Johns, 2014), it is not surprising that the relationship between LSD and the AMOC at 26^∘ N is much weaker. Nevertheless, the reasons behind the large spread in these relationships across models are not so clear.

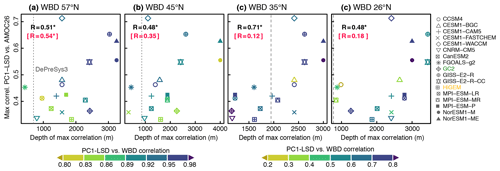
Figure 11 (a) Scatterplot of the maximum cross-correlation value in Fig. 4b between PC1-LSD and AMOC26 (without the Ekman component) against the depth at which the maximum correlations at any lag between PC1-LSD and the WBD at 57^∘ N occur. The maximum correlations are based on 10-year running trends. The correlation coefficient between the two metrics is shown in black the top left corner. Likewise, another correlation coefficient is shown in magenta, computed between the PC1-LSD and AMOC26 maximum correlation and the PC1-LSD and WBD at 57^∘ N maximum correlation. The presence of an asterisk indicates that the correlation is significant at the 95 % confidence level. Colours indicate the maximum correlation between PC1-LSD and the WBD. The grey vertical lines depict the corresponding depth of maximum correlation for the DePreSys3 assimilation run. (b–d) The same as in (a) but for the WBD at 45, 35, and 26^∘ N, respectively.

We have tried to constrain this uncertainty by looking at a range of observed metrics that may explain the spread in the correlation strength, including the density anomalies on the western boundary, the stratification of the Labrador Sea, and the mean AMOC strength. Overall, these constraints point to a relatively weak relationship between LSD and the AMOC at 26^∘ N on decadal timescales (i.e. r∼0.4) in the real world. However, there are many reasons why this number is still very uncertain, and further work is needed to assess its validity. A caveat of this study is that the simulations and observation-based datasets employed are not directly comparable, as they differ in the background radiative forcing levels, the length of the period used to compute the climatologies, and even the way some indices, like the AMOC, are computed. We also recognize that there is large uncertainty within the observationally derived metrics. For instance, the assimilation run in DePreSys3, which is used to constrain relationships, clearly underestimates the mean AMOC strength at 26^∘ N with respect to RAPID (see Fig. 8b) and therefore might also be underestimating the AMOC at higher latitudes. Our findings might also be limited by model deficiencies. There is emerging evidence that current models underestimate AMOC and North Atlantic variability on decadal timescales (Roberts et al., 2013; Cheung et al., 2017), which can degrade decadal predictability in the region and even lead to overly weak linkages between the AMOC and the AMV (Yan et al., 2018). The AMV is indeed a mode of variability that also shows important differences across models in terms of different aspects like its periodicity, amplitude, spatial structure, and climate footprints (Medhaug and Furevik, 2011; Zhang and Wang 2013; Kavvada et al., 2013); these are intermodel differences that could be partly connected to those reported herein for the PC1-LSD vs. AMOC relationships. Models also tend to generally underestimate the depth of the return flow, and this may still affect how density anomalies project on the basin-wide AMOC. It has also been argued that ocean-only models produce too much deep water in the western basin and Labrador Sea (i.e. Li et al., 2019), and recent observations even challenge the prevailing view from models that Labrador Sea convection dominates the AMOC variability (Koenigk and Brodeau, 2017), suggesting that the key deepwater formation occurs in the Irminger Sea a few hundred kilometres northeast of the Labrador Sea (Lozier et al., 2019). Therefore, further in-depth study is warranted to narrow down the uncertainty in the real AMOC and PC1-LSD relationship.

Most of the models considered in this study have relatively coarse resolution, including non-eddying oceans ($\ge \mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$), which means that they might be missing some key dynamics for the AMOC (Johnson et al., 2019) that could be important to represent realistic linkages. The current analysis also includes two models at eddy-permitting resolution (HadGEM3-GC2 and HiGEM), whose relationships lie within the spread of those in the coarser models. However, it could be that higher resolution is needed (e.g. enabling mesoscale eddies at subpolar latitudes) to identify substantial differences (Hirschi et al., 2020; Johnson et al., 2019). A recent analysis based on HadGEM3-GC3.1 (a later version of HadGEM3-GC2) configured at different horizontal resolutions has shown that long-standing model biases affecting the North Atlantic are reduced at eddy-resolving resolution ($\mathrm{1}/\mathrm{12}{}^{\circ }\times \mathrm{1}/\mathrm{12}{}^{\circ }$ in the ocean) and that the strength of the AMOC, the boundary currents, and the northward heat transport is higher than for the coarser resolutions (Hirschi et al., 2020; Roberts et al., 2019). High-resolution coupled models also generally support the new view from OSNAP observations that the largest fraction of AMOC variability (on sub-annual to decadal timescales) originates at the eastern SPNA (Hirschi et al., 2020). Eddy-resolving resolutions have also been shown in a multi-model study (Roberts et al., 2020) to represent the AMOC response at 26^∘ N differently in future projections, leading to stronger declines than in non-eddying simulations that are mostly associated with a weakening in the Florida Current. Roberts et al. (2020) also compare the meridional coherence of the AMOC, which does not seem to be resolution-dependent; this is a result that is in line with another multi-model comparison between non-eddying and eddy-permitting simulations (Li et al., 2019).

Despite the current limitations in the models considered for this study, it is important to highlight the fact that they provide a rather consistent picture of a chain of relationships in the North Atlantic that is able to explain some of the recent observed trends (Robson et al., 2016). This paper has broadly characterized this behaviour and highlighted the uncertainty. These relationships are also consistent with the mechanisms proposed by Yeager and Robson (2017) to explain high levels of predictive skill in the SPNA on decadal timescales. Our analysis has also helped to identify specific metrics (such as LSD stratification and the depth of the boundary density) that could be used as emergent constraints for future projections, i.e. to subset the simulations expected to more realistically represent the future changes in the region. Having a more realistic subpolar gyre stratification under present-day conditions has been shown in CMIP5 simulations to increase the probability of a future collapse in convection (Sgubin et al., 2017), which would lead to a widespread SPG cooling. It remains to be tested if similar conclusions can be drawn from eddy-resolving simulations.