Bayesian deconstruction of climate sensitivity estimates using simple models: implicit priors and the confusion of the inverse

Observational constraints on the equilibrium climate sensitivity have been generated in a variety of ways, but a number of results have been calculated which appear to be based on somewhat informal heuristics. In this paper we demonstrate that many of these estimates can be reinterpreted within the standard subjective Bayesian framework in which a prior over the uncertain parameters is updated through a likelihood arising from observational evidence. We consider cases drawn from paleoclimate research, analyses of the historical warming record, and feedback analysis based on the regression of annual radiation balance observations for temperature. In each of these cases, the prior which was (under this new interpretation) implicitly used exhibits some unconventional and possibly undesirable properties. We present alternative calculations which use the same observational information to update a range of explicitly presented priors. Our calculations suggest that heuristic methods often generate reasonable results in that they agree fairly well with the explicitly Bayesian approach using a reasonable prior. However, we also find some significant differences and argue that the explicitly Bayesian approach is preferred, as it both clarifies the role of the prior and allows researchers to transparently test the sensitivity of their results to it.

1 Introduction

While numerous explicitly Bayesian analyses of the equilibrium climate sensitivity have been presented (e.g. Tol and De Vos, 1998; Olson et al., 2012; Aldrin et al., 2012), many results have also been generated which appear to be based on more heuristic methods. In this paper we examine several such estimates and demonstrate how they can be reinterpreted in the context of the subjective Bayesian framework, revealing in each case an underlying prior which can be deemed to have been implicitly used. That is to say, we present an explicitly Bayesian analysis which takes the same observational data together with the same assumptions and model underlying the data-generating process, which (when used to update this implicit prior) precisely replicates the published result. In some cases these implicit priors exhibit rather unconventional properties, and we argue that they are unlikely to have been chosen deliberately and would probably not have been used if the authors had presented a transparently Bayesian analysis. We rerun some of these analyses in a standard Bayesian framework using the same observational evidence to update a range of explicitly stated priors. While in many cases these results are broadly similar to the existing published results, some differences will be apparent.

The paper is organised as follows. In Sect. 2 we introduce some concepts in Bayesian analysis which underpin our presentation. In Sect. 3, we explore several calculations in which researchers have estimated the climate sensitivity via direct calculation based on observationally derived probability density functions, considering paleoclimate research (Annan and Hargreaves, 2006; Köhler et al., 2010; Rohling et al., 2012), the observational record of warming over the 20th century warming (Gregory et al., 2002; Mauritsen and Pincus, 2017), and analyses of interannual variability (Forster and Gregory, 2006; Dessler and Forster, 2018) in turn. We present a Bayesian interpretation of these calculations and give some alternate analyses based on alternative, explicitly stated, priors. We argue that this latter approach is preferred, as it both clarifies the role of the prior and allows researchers to transparently test the sensitivity of their results to it. We conclude with a general discussion about our results.

2 Principles and methods

2.1 Confidence intervals, Bayesian probability, and the “confusion of the inverse”

Let us assume we have a measuring process that produces an observational estimate x_o of an unknown (but assumed constant) parameter which takes the value x_T, with an observational error ϵ that can be considered to take a specified error distribution, typically an unbiased Gaussian:

$$\begin{array}{}\text{(1)}& x_{\mathrm{o}}=x_{\mathrm{T}}+\mathit{ϵ},\end{array}$$

where $\mathit{ϵ}\sim N(\mathrm{0},\mathit{\sigma })$. For simplicity, we assume here that σ is known. This “measurement model” is fundamental to analysis of observations in many scientific domains. For example, in climate science, analyses of observed global temperature anomalies are commonly generated and presented in this form. We emphasise that the error term in this equation need not be defined solely in terms of a simple instrumental or sampling error but may include any and all sources of discrepancy between the numerical value generated from an observational analysis and the measurand that the researcher is interested in. Some examples will be discussed later when we present applications of our methodology. All that we require in order to use this equation is to assume that the uncertainty inherent in the generation of the observational estimate is independent of the true value which is being estimated and that we have a statistical model for it (such as Gaussian).

Following on from this measurement model, there is a simple syllogism (i.e. a logical argument) that seems common in many areas of scientific research, which runs as follows: since we know a priori that $p(-\mathrm{2}\mathit{\sigma }<\mathit{ϵ}<\mathrm{2}\mathit{\sigma })\simeq \mathrm{95}$ %, we can also write a posteriori that $p(x_{\mathrm{o}}-\mathrm{2}\mathit{\sigma }<x_{\mathrm{T}}<x_{\mathrm{o}}+\mathrm{2}\mathit{\sigma })\simeq \mathrm{95}$ % once x_o is known. For example, if σ=0.25 is given and we observe the value x_o=74.60, then the researcher may assert that there is a ∼95 % probability that x_T lies in the interval (74.10, 75.10) or simply present a full probability density: the probability distribution function (PDF) of x_T is $N(x_{\mathrm{o}},\mathit{\sigma })=N$(74.60, 0.25).

This syllogism is intuitively appealing but incorrect. It appears to arise from the misinterpretation of frequentist confidence intervals as being Bayesian credible intervals. We should note that calculating and presenting the interval x_o±2σ as a frequentist 95 % confidence interval would be a valid procedure. That is to say, if we were to repeatedly take a new observation x_o according to Eq. (1), with each observation having an independent observational error of standard deviation 0.25, and generate the corresponding interval (x_o−0.5, x_o+0.5) then approximately 95 % of the intervals so generated would include the true value x_T. However, frequentist confidence intervals are not the same thing as Bayesian credible intervals. The latter interpretation for an interval refers to a degree of belief that the particular interval that has been generated on a specific occasion does in fact include the parameter. Climate scientists are far from unique in this misinterpretation, which appears to be widespread throughout the scientific community (Hoekstra et al., 2014). Because this misunderstanding is so deeply embedded in scientific practice and discourse, we now discuss and explain it in some detail.

We start by noting that probabilistic statements concerning the true value x_T demand the use of the Bayesian paradigm wherein the language and mathematics of probability may be applied to events that are not intrinsically random, but about which our knowledge is uncertain (Bernardo and Smith, 1994). The parameter x_T itself does not have a probability distribution here; it was assumed to take a fixed value. Therefore, to even talk of the PDF of x_T in this manner is to commit a category error. It is the researcher's beliefs concerning x_T that are uncertain, and this uncertainty is represented as their PDF for x_T.

Bayes' theorem is a simple consequence of the axioms of probability: the joint density p(x_o,x_T) of two variables x_o and x_T can be decomposed in two different ways via

$$p\left(x_{\mathrm{o}},x_{\mathrm{T}}\right)=p\left(x_{\mathrm{T}}|x_{\mathrm{o}}\right)p\left(x_{\mathrm{o}}\right)=p\left(x_{\mathrm{o}}|x_{\mathrm{T}}\right)p\left(x_{\mathrm{T}}\right)$$

and thus

$$\begin{array}{}\text{(2)}& p\left(x_{\mathrm{T}}|x_{\mathrm{o}}\right)=p\left(x_{\mathrm{o}}|x_{\mathrm{T}}\right)p\left(x_{\mathrm{T}}\right)/p\left(x_{\mathrm{o}}\right).\end{array}$$

p(x_T|x_o) is our posterior density for the true value x_T given the observational evidence x_o. p(x_T) is the prior distribution for x_T, which describes the researcher's belief excluding the observational evidence. p(x_o|x_T) is commonly termed the “likelihood” and is determined by the measurement model: for example, in the case of an unbiased Gaussian observational error, such as in Eq. (1), the functional form of p(x_o|x_T) is given by

$$p\left(x_{\mathrm{o}}|x_{\mathrm{T}}\right)={\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{2}\mathit{\pi }}\mathit{\sigma }}}{e}^{\frac{-{\left(x_{\mathrm{o}}-x_{\mathrm{T}}\right)}^{\mathrm{2}}}{\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}}}}.$$

When the terms for x_o and σ are replaced in this function by their known numerical values, this function looks like it could be a probability distribution for p(x_T|x_o), but as Bayes' theorem (Eq. 2) makes clear, it is not in general the posterior PDF, instead being merely one term in its calculation. This is the critical point which underpins the analyses presented in this paper: the distribution of the observation defined by measurement models such as Eq. (1) directly defines the likelihood p(x_o|x_T) and not the posterior PDF p(x_T|x_o).

The error in the syllogism is to interpret p(x_o|x_T) as p(x_T|x_o): this is a common fallacy known as the confusion of the inverse, which is closely related to the “prosecutor's fallacy”, the latter term generally being used in discrete probability in which the phenomenon is more widely known and well studied. The fallacy is perhaps easiest to illustrate with discrete cases which compare P(A|B) to P(B|A) for a pair of events A and B. For example, the probability of a person suffering from a rare disease (event A), given that they tested positive for it (event B), is in general different from (and often rather lower than) the probability that someone produces a positive test result given that they are suffering from the disease. It has been known for some time that medical doctors routinely commit this transposition error (Gigerenzer and Hoffrage, 1995). Additional examples and a further discussion of this type of fallacious reasoning in relation to interval estimation can be found in Morey et al. (2016).

We now present a simple example in which the syllogism leads to poor results in a physically based scenario with continuous data. We take as given that the timing error of a handheld stopwatch is ±0.25 s at 1 standard deviation (Hetzler et al., 2008). That is to say, the measured time t_o is related to the true time, t_T, via $t_{\mathrm{o}}=t_{\mathrm{T}}+\mathit{ϵ}$ with $\mathit{ϵ}\sim N(\mathrm{0},\mathrm{0.25})$ (see Eq. 1). Let us consider an experiment in which an adult male colleague holds a dense object (say, a stone) at head height while standing and drops it while the experimenter times how long it takes for the stone to reach the ground.

An observed time of t_o=0.60 s could lead someone to say via the confusion of the inverse fallacy that the true time taken is represented by the Gaussian PDF t_T∼N(0.6, 0.25) (albeit with an assumed truncation at zero which we ignore for convenience). One implication of this PDF is that there is a 16 % chance that the true time is less than 0.35 s and also a 16 % chance that it is more than 0.85 s. Ignoring the negligible air resistance and using the simple equation of motion under gravity $h=\frac{\mathrm{1}}{\mathrm{2}}a{t}^{\mathrm{2}}$, one would have no choice but to conclude from these values that the experimenter's colleague has a 16 % chance of being less than 60 cm tall and also a 16 % chance of being greater than 4.5 m tall. For a typical adult male, neither of these cases seems reasonable. We have obtained a measurement which is entirely unremarkable, with the observed time corresponding to a fall of around 1.75 m. And yet the commonplace interpretation of an imprecise measurement as directly giving rise to a probability distribution for the measurand has led to palpably ridiculous results. While in many cases the results will not be so silly, this simple example does demonstrate that the methodology cannot be sound. The more pernicious cases are those in which the interpretation is not so obviously silly and thus may be confidently presented, even though the methodology is still (as we have just shown) invalid.

In order to make sensible use of this observation, we can instead perform a simple Bayesian updating procedure. The distribution N(0.6, 0.25) is actually correctly interpreted as the likelihood of the observed time p(t_o|t_T), which can be used to update a prior estimate. The distribution of adult male heights in the UK (in metres) is taken to be N(1.75, 0.07), and we use this as our prior. The drop time t predicted from a height drop h is given by $t=\sqrt{\mathrm{2}h/a}$, where a=9.8 m s⁻² is the acceleration due to gravity. Due to the substantial observational uncertainty, the likelihood of the drop time is virtually flat across the support of the prior, varying by less than 1 % across the range of 1.60 to 1.90 m. The posterior estimate obtained through Bayes' theorem is easily calculated by direct numerical integration and still approximates to N(1.75, 0.07) to two decimal places. The correct interpretation of the experiment is not, therefore, that the measurement shows there is a substantial probability of the researcher breaking a height record, but rather that the measurement is so imprecise that it does not add any significant information on top of what was already known.

While it is formally invalid, we must acknowledge that this syllogism does actually work rather well in many cases. In particular, if the likelihood p(x_o|x_T) is non-negligible over a sufficiently small neighbourhood of x_o such that a prior can reasonably be used which is close to uniform in this region of x_o, then the true posterior calculated by a Bayesian analysis will be close to that asserted by the syllogism. For example, if the Gaussian prior x_T∼N(100, 20) were to be used in the original example, then when this is updated by the likelihood corresponding to the observation x_o=74.6 with uncertainty σ=0.25, the correct posterior p(x_T|x_o) is actually given by N(74.6, 0.25) to several significant digits. In the limiting case in which an unbounded uniform prior is used for x_T, the syllogism is precisely correct.

Thus, in practice the syllogism can often be interpreted as a Bayesian analysis in which a uniform prior has been implicitly used, and in cases in which this is reasonable it will generate perfectly acceptable results. Statements to this effect have occasionally appeared in some papers wherein a non-Bayesian analysis has been presented as directly giving rise to a posterior PDF. It may therefore seem that the terms “fallacy” and “confusion” are somewhat melodramatic: this convenient shortcut is often harmless enough. However, this cannot be simply asserted without proof: there are many examples of procedures for generating frequentist confidence intervals in which the results cannot plausibly be interpreted as Bayesian credible intervals (Morey et al., 2016). In addition to concerns over the prior, it is also essential when taking this shortcut that the observational uncertainty σ is taken to be a constant which does not vary with the parameter of interest x_T. This may be the case when we consider uncertainties arising solely from an observational instrument but is less clear when σ includes a contribution from the system under study. For example, if the uncertainty in an observed estimate of the forced temperature response in an analysis of climate change includes a contribution due to the internal variability of the climate system, then this internal variability might be expected to vary with the parameters of the system. In this case, an answer generated via the confusion of the inverse cannot be rescued by the invocation of a uniform prior. However, we do not explore this uncertainty in σ further in this paper.

Some have attempted to retrospectively defend the use of this syllogism with the claim that the uniform prior is necessarily the correct one to use, generally via the belief that this represents some sort of pure or maximal state of ignorance. However, it is well established (and indeed is sometimes used as a specific point of criticism) that there is no such thing as pure ignorance within the Bayesian framework. See Annan and Hargreaves (2011) for a further discussion of this in the context of climate science. Our objection to the widespread application of this procedure is perhaps best summed up by Morey et al. (2016), who state the following: “Using confidence intervals as if they were credible intervals is an attempt to smuggle Bayesian meaning into frequentist statistics, without proper consideration of a prior.” There is also a strand of Bayesianism which asserts more broadly that in any given experimental context there is a single preferred prior, typically one which maximises the influence of the likelihood in some well-defined manner. The Jeffreys prior is one common approach within this “objective Bayesian” framework. However, it has the disadvantage that it assigns zero probability to events that the observations are uninformative about. This “see no evil” approach does have mathematical benefits but it is hard to accept as a robust method if the results of the analysis are intended to be of practical use. In the real world, our inability to (currently) observe something cannot rationally be considered sufficient reason to rule it out. We do not consider objective Bayesian approaches further.

It is a fundamental assumption of this paper that in the cases presented below, in which researchers have presented observational estimates of temperature change ΔT_o in the form $\mathrm{\Delta }{T}_{\mathrm{o}}=\mathit{\mu }\pm \mathit{\sigma }$ or in some equivalent manner, they are (perhaps implicitly) using a measurement model of the form given in Eq. (1) with μ representing the observational value obtained and σ representing the expected magnitude of observational uncertainty (assumed Gaussian throughout this paper, as is common in the literature). On this basis, the temperature observation gives rise to a likelihood as described above and does not directly generate a probability distribution for ΔT_T. We note, however, that authors have not always been entirely clear about the statistical framework of their work and it is not always possible to discern their intentions precisely. Thus, while we confidently believe our interpretation to be natural and appropriate in many cases, we do not claim it to be universally applicable.

2.2 Priors for the climate sensitivity

Most probabilistic estimates of the equilibrium climate sensitivity which have explicitly presented a Bayesian framework have used a prior which is uniform in sensitivity S. There does not appear to be any principled basis for this choice, which has been argued on the basis that it represented “ignorance”. One could just as easily (and erroneously) argue that a prior which is uniform in feedback $\mathit{\lambda }=F_{\mathrm{2}\times }/S$ was ignorant (here F_2× is the forcing arising from a doubling of CO₂). In fact, both of these improper priors can exhibit a pathology which causes problems with their use. In particular, if the likelihood is non-zero at λ=0 (S=0), then when the improper unbounded uniform prior on S (λ) is used, the posterior will also be improper and unbounded. In practical applications, this problem has generally been masked by the use of an upper bound on the prior, but (while a lower bound of 0 may be defended on the basis of stability) the choice of the upper bound is hard to justify. The upper bound which appears to have been most commonly used for sensitivity is 10 ^∘C, and we will adopt this choice here. We use a range of 0.37–10 for the uniform priors in both λ and S, which ensures that their ranges are numerically identical (although their units are of course different). As a third alternative prior for S, we will also use the positive half of a Cauchy prior, with location 0 and scale parameter 5, i.e. $p\left(S\right)=\frac{\mathrm{2}}{\mathrm{5}\mathit{\pi }(\mathrm{1}+(S/\mathrm{5}{)}^{\mathrm{2}})}$, S>0. An attractive feature of the Cauchy prior is that it has a long tail which only decreases quadratically (hence, it does not rule out high vales a priori); moreover, its inverse is also Cauchy, so both S and λ have broad support. The scale factor is the 50th percentile of the distribution; hence, the half-Cauchy prior for S has a 50 % probability of exceeding 5 ^∘C. The scale factor of the corresponding implied prior in λ is given by $\mathrm{3.7}/\mathrm{5}=\mathrm{0.74}$ W m⁻² K⁻¹.

3 Applications

We now consider three areas in which observational constraints have been used to estimate the equilibrium climate sensitivity. Firstly, we consider paleoclimatic evidence, which relates to intervals during which the climate was reasonably stable over a long period of time and significantly different to the pre-industrial state. We then consider analyses of observations of the warming trend over the 20th century (strictly, extending into the 21st and 19th century). Finally, we consider analyses of interannual variability.

3.1 Paleoclimate

3.1.1 Observationally derived PDFs

A common paradigm for estimating the equilibrium climate sensitivity S using paleoclimatic data is to consider an interval in which the climate was reasonably stable and significantly different to the present and analyse proxy data, such as pollen grains and isotopic ratios in sediment cores, in order to generate estimates of the forced global mean temperature anomaly ΔT caused by the forcing anomaly ΔF relative to the current (pre-industrial) climate. S can then be estimated via the equation

$$\begin{array}{}\text{(3)}& S=F_{\mathrm{2}\times }\times \mathrm{\Delta }T/\mathrm{\Delta }F,\end{array}$$

where F_2× is the forcing due to a doubling of the atmospheric CO₂ concentration. Examples of this approach include Annan and Hargreaves (2006) and Rohling et al. (2012).

The interval which has been examined in the most detail in this manner is probably the Last Glacial Maximum at 19–23 ka (Mix et al., 2001) when the climate was reasonably stable (at least in the sense of gross evaluations such as global mean surface air temperature on millennial timescales) and substantially different to the present day such that the signal-to-noise ratio in estimates of forcing and temperature change is reasonably high.

The method adopted by Annan and Hargreaves (2006) and we believe many others (although this is not always documented explicitly), which we term sampling the observational PDFs, was to generate an ensemble of values of S by repeatedly drawing pairs of samples from PDFs, which are deemed to represent estimates of the forcing and temperature anomalies, and calculating for each pair the corresponding value of S using Eq. (3). The ensemble of values for S so generated is then considered to be a representative sample from a probabilistic estimate of the truth.

Using values based broadly on those used in Annan and Hargreaves (2006, 2013), Köhler et al. (2010), and Rohling et al. (2012), we use observational estimates of 5±1.5 ^∘C for ΔT and 9±2 W m⁻² for ΔF (with the uncertainties here assumed to represent 1 standard deviation of a Gaussian), along with a fixed value for F_2× of 3.7 W m⁻². In the illustrative calculations presented here we ignore any issues relating to the non-constancy of the sensitivity S and how it might vary in relation to the background climate state and nature of the forcing, although we have slightly inflated the uncertainties of the observational constraints in order to make some attempt to compensate for this. Thus, the numerical values generated here are not intended to be definitive but are still adequate to illustrate the different approaches.

As mentioned in Sect. 2.1, we assume that published estimates for ΔT can be understood as representing likelihoods p(ΔT_o|ΔT_T) – that is to say, the observational analysis provides an uncertain estimate of the true value of the form given by Eq. (1) with an a priori unbiased error of the specified value. The analysis of Annan and Hargreaves (2013) certainly follows this paradigm, with the estimate of the uncertainty being informed by a series of numerical experiments in which the estimation procedure was tested on artificial datasets in order to calibrate its performance. For the forcing estimate, things are not so clear. We do not have direct proxy-based evidence for the forcing, which is typically estimated based on a combination of modelling results and some rather subjective judgements (Köhler et al., 2010; Rohling et al., 2012). Any uncertainty in the actual measurements involved, such as those of greenhouse gas concentrations in bubbles in ice cores, makes a negligible contribution to the overall uncertainty in total forcing. Therefore, we do not have a clear measurement model of the form given in Eq. (1) with which to define a likelihood for the forcing. Thus, we take the stated distribution to directly represent a prior estimate for the forcing anomaly. We do not claim that this is the only reasonable approach to take here, and other researchers might prefer to make different choices, in particular if they could clearly identify a likelihood arising from observational data.

When applied to the numerical estimates provided above, the PDF sampling method of Annan and Hargreaves (2006) generates an ensemble for S with a median estimate of 2.1 ^∘C and a 5 %–95% range of 1.0 to 3.8 ^∘C. Figure 1 presents this result as the cyan line, together with additional results which will be described below.

Figure 1 Prior and posterior estimates for the climate sensitivity arising from paleoclimatic evidence. Dashed lines show priors, and solid lines are posterior densities. The thick cyan line shows the posterior estimate arising from the method of sampling observational PDFs, with the corresponding prior shown in Fig. 2. Blue lines represent results using a uniform prior in λ; red is uniform in S, and magenta is half-Cauchy (scale: 5) in S (and therefore also half-Cauchy in λ; scale: 3.7∕5).

3.1.2 Bayesian interpretation and alternative priors

Now we present alternative calculations which take a more standard and explicitly Bayesian approach. We start by writing the model in the form

$$\begin{array}{}\text{(4)}& \mathrm{\Delta }T=S\times \mathrm{\Delta }F/\mathrm{3.7},\end{array}$$

or equivalently

$$\begin{array}{}\text{(5)}& \mathrm{\Delta }T=\mathrm{\Delta }F/\mathit{\lambda },\end{array}$$

where $\mathit{\lambda }=S/\mathrm{3.7}$ is the feedback parameter. This formulation allows us to easily consider the forcing and feedback parameter to be uncertain inputs (for which we can explicitly define prior distributions) to the model, which can then be updated by the likelihood arising from the observed temperature change.

Although the method of sampling observational PDFs described in Sect. 3.1.1 was not presented in Bayesian terms, we are now in a position to present a Bayesian interpretation of it. The distribution generated by sampling the PDFs is distributed as independently Gaussian N(5, 1.5) in ΔT and Gaussian N(9, 2) in ΔF. We aim to choose a prior such that the Bayesian analysis will generate this as the posterior after updating by the likelihood for ΔT. This likelihood as described above is taken to be the Gaussian N(5, 1.5). Therefore, by rearrangement of Bayes' theorem, the desired prior must be uniform in ΔT and independently Gaussian N(9, 2) in ΔF. For numerical reasons we must impose bounds on the uniform prior for ΔT, and we set this range to be 0–20 ^∘C.

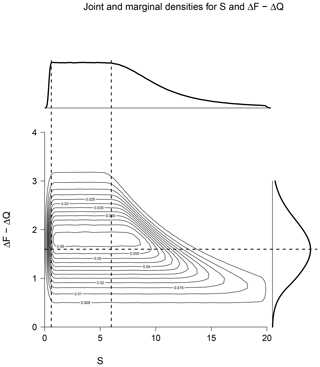
Using Eq. (3), we can re-parameterise this joint prior distribution over ΔT and ΔF into a distribution over S and ΔF, and this is presented in Fig. 2. Note that this prior cannot be represented as the product of independent distributions over S and ΔF, as high S here is correlated with low ΔF and vice versa. The prior in S when viewed as a marginal distribution (i.e. after integrating over ΔF) appears uniform over a significant range (roughly between S=0.6 and S=5), but within this range it is associated with somewhat high values for ΔF, with the latter taking a mean value of about 9.5 W m⁻² over this region. The details of the shape of this joint prior depend on the bounds placed on the uniform prior for ΔT, but this does not affect the posterior so long as the prior is broad enough to cover the neighbourhood of the observation. We think it is unlikely that researchers would choose a joint prior of this form deliberately and confirm that this certainly was not the case in Annan and Hargreaves (2006). In future analyses it would seem more appropriate to clearly state the priors which are used and test the sensitivity of the results to this choice.

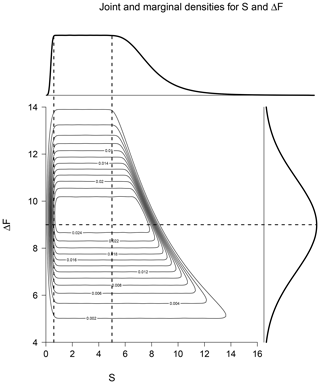
Figure 2 Implicit prior used in the paleoclimate estimate. The contour plot shows the joint prior in S and ΔF with marginal densities shown at the top and right, respectively. Vertical and horizontal dashed lines are drawn at S=0.6, 5, and ΔF=9.

In order to perform a more conventional Bayesian updating procedure using Eq. (5), we must first select priors on the model inputs. Since the sensitivity is a property of the climate system, whereas the forcing is specific to the interval we are considering, we define their priors independently. For the forcing ΔF, we retain the N(9, 2) prior, having no plausible basis for trying anything different. For sensitivity, we test the three priors described in Sect. 2.2. The two uniform priors generate rather different results. Using a prior which is uniform in S, the posterior has a mean value for S of 2.2 ^∘C and a 5 %–95% range of 1.0–4.2 ^∘C. When we change to uniform in λ the median decreases to 1.5 ^∘C with a 5 %–95% range of 0.5–3.0 ^∘C. While these results, which are shown in Fig. 1, overlap substantially, broadening the upper bounds on the priors would result in the first result increasing without limit and the second decreasing towards zero such that they would fully separate. We therefore see that extreme choices for the prior on S (or λ) can have a significant influence on Bayesian estimation, which is perhaps not surprising given the large uncertainties in the observational constraints used here. The median posterior value for S obtained from the half-Cauchy prior is 2.1 ^∘C with a 5 %–95% range of 1.0–3.8 ^∘C, which coincidentally aligns very closely with the result obtained by the naive method of sampling observational PDFs (which is plotted as a thick line in Fig. 1 in order to make it more visible). We conclude in this case that the method of sampling PDFs has generated a result which is reasonable, but alternative choices of the prior could give noticeably different results.

3.2 Estimates based on historical warming

3.2.1 Observationally derived PDFs

Perhaps the most common approach to estimating S has been to use the instrumental record (Tol and De Vos, 1998; Gregory et al., 2002; Olson et al., 2012; Aldrin et al., 2012). While a wide range of climate models have been utilised for this purpose, a simple energy balance similar to that of Sect. 3.1 can be used so long as the radiative imbalance is accounted for. We follow the recent analysis of Mauritsen and Pincus (2017) but simplify their calculation by ignoring uncertainty in F_2×, instead adopting their mean value of 3.71 W m⁻² (using all their uncertain numerical values otherwise). This simplification has very little influence on the results. Mauritsen and Pincus (2017) present the basic energy balance in the form

$$\begin{array}{}\text{(6)}& S=F_{\mathrm{2}\times }\mathrm{\Delta }T/(\mathrm{\Delta }F-\mathrm{\Delta }Q),\end{array}$$

where ΔQ represents the net planetary radiative imbalance and the other terms are as before. We emphasise that ΔT here specifically denotes the forced temperature change. This equation is applied between two widely separated decadal-scale intervals within the historical record such that the signal-to-noise ratio in the temperature change (and hence precision in the resulting estimate of S) is as large as possible, though it remains a significant source of uncertainty (Dessler et al., 2018). Similar to Sect. 3.1.1, the method used by Mauritsen and Pincus (2017) is one of sampling observationally derived PDFs for all uncertain quantities on the right-hand side of Eq. (6), thereby generating an ensemble of values for S which was interpreted as a probability distribution.

3.2.2 Bayesian interpretation and alternative priors

As in Sect. 3.1.2, we reorganise Eq. (6) in order to give ΔT as the prognostic variable, assigning priors to the terms on the right-hand side. We thus obtain

$$\begin{array}{}\text{(7)}& \mathrm{\Delta }T=(\mathrm{\Delta }F-\mathrm{\Delta }Q)\times S/F_{\mathrm{2}\times }=(\mathrm{\Delta }F-\mathrm{\Delta }Q)/\mathit{\lambda }.\end{array}$$

We adopt the distributions used by Mauritsen and Pincus (2017) for ΔF and ΔQ as priors for these variables but interpret their estimate for the temperature change ΔT_o as a likelihood $p\left(\mathrm{\Delta }{T}_{\mathrm{o}}\right|\mathrm{\Delta }T)\sim N$(0.77, 0.08) arising from the measurement model of Eq. (1). This arises immediately from the paradigm of the observed total temperature response consisting of the forced response summed together with a contribution from internal variability which can be assumed independent of the forced response itself. In this case, the analysis of observed temperatures generated the (deterministic) value ΔT_o=0.77 ^∘C, with the uncertainty estimate being separately derived as an estimate for the likely contribution of internal variability to a temperature change over such a time interval (Lewis and Curry, 2014). True measurement errors in the calculation of ΔT_o are sufficiently small relative to this internal variability that they can be safely ignored.

Given the similarities between Eqs. (3) and (6), and also in the method used, it is no surprise to find that the implicit prior used here before updating with the temperature likelihood is qualitatively similar to that found in Sect. 3.1. This is shown in Fig. 3. Again, the marginal prior over S appears uniform over a reasonable range (the details depend on the limits of the uniform prior over ΔT), but nevertheless it is actually correlated with the net forcing. Figure 4 shows the posterior result arising from this prior, which matches the published result of Mauritsen and Pincus (2017) closely despite our minor simplification to their calculation. The posterior median calculated here is 1.8 ^∘C with a 5 %–95% range of 1.1–4.5 ^∘C. As in Sect. 3.1, we make no attempt to decompose the forcing estimate used here into a prior and likelihood, especially as some of the largest uncertainties (e.g. that arising from aerosol forcing) are based on modelling calculations and expert judgements that cannot be transparently traced to uncertainties in observational data.

Figure 3 Implicit prior used in the 20th century estimate.

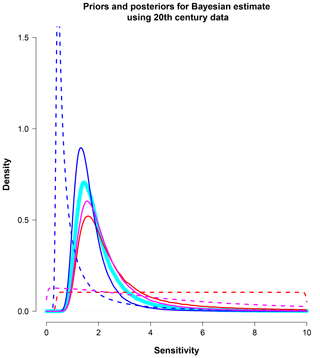
Figure 4 Priors and posteriors in explicit Bayesian estimates using 20th century data. Dashed lines show priors, and solid lines are posterior densities. The thick cyan line shows the posterior estimate arising from the method of sampling observational PDFs, with its implicit prior shown in Fig. 3. Blue lines represent results using a uniform prior in λ; red is uniform in S, and magenta is half-Cauchy (scale: 5) in S (and therefore also half-Cauchy in λ; scale: 3.7∕5).

Alternative priors and their resulting posteriors after Bayesian updating using Eq. (7) are shown in Fig. 4. As before, we test the three priors presented in Sect. 2.2. The posterior median values (and 5 %–95% range) for S arising from these are 2.1 ^∘C (1.2–6.3 ^∘C) for uniform S, 1.5 ^∘C (1.0–3.1 ^∘C) for uniform λ, and 2.0 ^∘C (1.1–5.0 ^∘C) for the half-Cauchy prior. Thus, again the half-Cauchy prior produces a result which is intermediate between the other explicit choices, though this time it has a somewhat longer tail than the PDF sampling method. The differences between these results, especially for the upper 95 % limit, are substantial and could significantly alter their interpretation and impact.

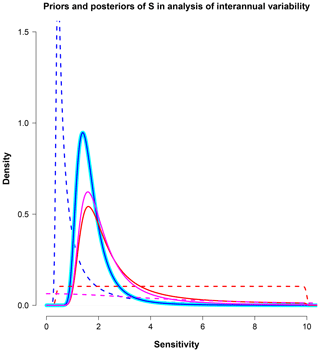
Figure 5 Priors and posteriors over S in a process-based feedback analysis. Dashed lines indicate priors, and solid lines are posteriors. The thick cyan line shows the posterior estimate arising from the method of sampling observational PDFs, which coincides precisely with the blue line that corresponds to the uniform prior in λ. Red lines show results using a uniform prior in S, and magenta is half-Cauchy (scale: 5) in S.

3.3 Estimates based on interannual variability

3.3.1 Observationally derived PDFs

Finally, we consider a method which has been used to estimate the climate sensitivity via interannual variation in the radiation balance and temperature (Forster and Gregory, 2006; Dessler and Forster, 2018). The basic premise of these analyses is that the feedback parameter can be estimated as the slope of the regression line of the net radiation imbalance (based primarily on satellite observations) against temperature anomalies, with data typically averaged on an annual timescale (though seasonal data may also be used). There are questions as to whether this short-term variability provides an accurate estimate of long-term changes, but this is beyond the scope of this paper (Dessler and Forster, 2018). The regression slope and its uncertainty naturally translate into a Gaussian likelihood for the true feedback component and have been commonly interpreted as a probability distribution for λ. While this again appears on the face of it to commit the fallacy of confusion of the inverse, the implicit assumption of a uniform prior on λ that underpins this interpretation has been clearly acknowledged by authors working in this area (e.g. see comments in Forster and Gregory, 2006; Forster, 2016). In this section we will use the observational estimate of Forster and Gregory (2006), which is given by ${\mathit{\lambda }}_{\mathrm{o}}=\mathrm{2.3}\pm \mathrm{0.7}$ W m⁻² K⁻¹. We note that when uncertainty in the forcing arising from a doubling of CO₂ is ignored, there is a trivial transformation between λ and S via $S=F_{\mathrm{2}\times }/\mathit{\lambda }$. Therefore, a likelihood for λ can be directly interpreted as an equivalent likelihood for S.

3.3.2 Bayesian interpretation and alternative priors

As noted by Forster and Gregory (2006), presenting what actually amounts to an observational likelihood for λ as a posterior PDF is equivalent to assuming a uniform prior in λ (see also Annan and Hargreaves, 2011). Therefore, the Bayesian interpretation is already clear in this instance.

In Fig. 5 we present the results of calculations using our three alternative priors (although one of them coincides with the method of sampling PDFs). The original result of Forster and Gregory (2006) (after transforming to S space) is represented by the blue lines, with red showing the result obtained for a uniform prior in S and magenta being a Cauchy prior. We note that, for the uniform S case, if the upper bound on the prior was raised, the posterior would also increase without limit due to the pathological behaviour discussed in Sect. 3.1.2 and also by Annan and Hargreaves (2011). For the priors shown (with the uniform priors defined as U[0.37, 10]) the 5 %–95% ranges of the posteriors are 1.1–3.2, 1.2–6.9, and 1.2–5.2 ^∘C for the uniform λ, uniform S, and Cauchy S priors, respectively. The uniform λ prior commonly adopted by analyses of this type provides a strong tendency towards low values, and the contrast with uniform S, especially for the upper bound, is disconcerting.

4 Conclusions

We have shown how various calculations which have presented probabilistic estimates of the equilibrium climate sensitivity S can be reinterpreted within a standard Bayesian framework. Using this standard framework ensures a clear distinction between the prior choices, which must be made for model parameters and inputs, and the likelihood obtained from observations of the system, which is then used to update this prior in order to generate the posterior.

In many cases, the implied prior for S which (according to this interpretation) underlies the published results appears somewhat unnatural, having either a structural relationship with model inputs or a marginal distribution that may not be considered reasonable. We have presented alternative calculations in which a range of simple priors are tested. In addition to the commonly used uniform priors, we have shown that a Cauchy prior has some attractive features in that it extends to high values (refuting any suspicion that the results obtained were simply constrained by the prior), and its reciprocal is also Cauchy (so both S and λ may have long tails). The half-Cauchy distribution used in this paper only requires a single scale parameter which determines the width. However, the choice of priors is always subjective, and we make no assertion that this choice should be universally adopted. Indeed, there may be superior alternative choices that we have not considered.

Our calculations suggest that the PDF sampling method can generate acceptable results in some cases, agreeing fairly well with a fully Bayesian approach using reasonable priors. However, this is not always the case. We recommend that researchers present their analysis in an explicitly Bayesian manner as we have done here, as this allows the influence of the prior and other uncertain inputs to be transparently tested.