the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Interannual variability in the gravity wave drag – vertical coupling and possible climate links
Petr Šácha
Jiri Miksovsky
Petr Pisoft
Gravity wave drag (GWD) is an important driver of the middle atmospheric dynamics. However, there are almost no observational constraints on its strength and distribution (especially horizontal). In this study we analyze orographic GWD (OGWD) output from Canadian Middle Atmosphere Model simulation with specified dynamics (CMAM-sd) to illustrate the interannual variability in the OGWD distribution at particular pressure levels in the stratosphere and its relation to major climate oscillations. We have found significant changes in the OGWD distribution and strength depending on the phase of the North Atlantic Oscillation (NAO), quasi-biennial oscillation (QBO) and El Niño–Southern Oscillation. The OGWD variability is shown to be induced by lower-tropospheric wind variations to a large extent, and there is also significant variability detected in near-surface momentum fluxes. We argue that the orographic gravity waves (OGWs) and gravity waves (GWs) in general can be a quick mediator of the tropospheric variability into the stratosphere as the modifications of the OGWD distribution can result in different impacts on the stratospheric dynamics during different phases of the studied climate oscillations.
- Article
(23560 KB) - Full-text XML
-
Supplement
(3764 KB) - BibTeX
- EndNote
Although the internal gravity wave (GW) sourcing (Plougonven and Zhang, 2014), propagation and breaking is governed to some extent by processes in the stratosphere, there is a significant portion of the GW spectra created in the troposphere (Alexander et al., 2009). The highest-amplitude upward-propagating modes can break already in the troposphere and lower or middle stratosphere (Fritts et al., 2016). Model experiments with gravity wave drag (GWD) parameterization showed that the orographic GWD in the lower stratosphere can significantly affect the development of the sudden stratospheric warming (Lawrence, 1997; Pawson, 1997; White et al., 2017, 2018; Šácha et al., 2016) and the large-scale flow in the lower stratosphere and troposphere in general (Alexander and Shepherd, 2010; McFarlane, 1987; Sandu et al., 2016; White et al., 2017; Šácha et al., 2016). In the global climate models, non-orographic GWs are usually considered to break in the upper stratosphere and higher above (Scinocca, 2003). It is well recognized that there is a need for continued and additional research efforts on stratospheric dynamics (Añel, 2016) as complex understanding and unbiased modeling of stratospheric conditions is vital for climate research (Calvo et al., 2015; Manzini et al., 2015).
From sensitivity simulations with a mechanistic model, Šácha et al. (2016) demonstrated the dynamical impact of the artificially enhanced GWD in the stratosphere and most importantly the significant impact of the spatial GWD distribution. This can open new horizons for research on teleconnections between tropospheric (e.g., El Niño–Southern Oscillation, North Atlantic Oscillation, Pacific Decadal Oscillation) and stratospheric (e.g., polar vortex stability) phenomena taking into account that the tropospheric variability can affect the distribution of GW sources and therefore the GWD distribution (and strength) in the stratosphere. This is also the main hypothesis that we investigate in this study. It is not possible to compute the GWD from current satellite observations alone (Alexander and Sato, 2015; Geller et al., 2013). Only by employing substantial approximation and neglecting observational filter effects, Ern et al. (2011) gave a methodology to estimate absolute values of a “potential acceleration” caused by GWs. Some information can also be derived using ray-tracing simulations (Kalisch et al., 2014). However, numerical simulations remain the major source of the GWD variability global description. This is also the reason why we study the interannual variability in the GWD using output from the Canadian Middle Atmosphere Model with specified dynamics (CMAM-sd) in this paper. Although the orographic GW parameterization schemes present a severe simplification of reality (Kalisch et al., 2014), they are the only available source providing three-dimensional decadal-long information on the GWD that is necessary to test the hypothesis of a connection between climate oscillations and GWD distribution. To our knowledge the interannual variability in GW model parameterization outputs has not been studied before. The study is structured as follows. The next section introduces the model, CMAM-sd simulation and the orographic GWD (OGWD) parameterization scheme together with statistical methods used in our study. The second section is dedicated to the OGWD analysis, assessing the realism of its climatology first. This is followed by an interannual variability analysis where significant differences in the distribution of OGWD depending on the Southern Oscillation (SO), North Atlantic Oscillation (NAO) and quasi-biennial oscillation (QBO) are illustrated. In the third section we examine the correspondence of OGWD to tropospheric conditions and analyze the variability in orographic gravity wave (OGW) momentum fluxes at the 850 hPa level. Finally, a summary of results and a discussion of the uncertainties and implications of our paper are given.
2.1 CMAM-sd and its GWD parameterizations
The CMAM chemistry climate model with 71 levels up to about 100 km with variable vertical resolution and a triangular spectral truncation of T47, corresponding to a 3.75∘ horizontal grid, has been used for producing the specified dynamics (sd) simulation of the time period between 1979 and 2010. Up to 1 hPa the horizontal winds and temperatures are nudged to the 6 hourly horizontal winds and temperatures from ERA-Interim (Dee et al., 2011), as described in more detail in McLandress et al. (2013). Due to this nudging, CMAM not only realistically reproduces the climate characteristics of real atmosphere but also follows its historical trajectory in a deterministic sense. This also applies to the activity of internal climate variability modes and their spatial response patterns, as illustrated by the samples in Figs. S1 and S2 in the Supplement.
OGWD is parameterized using the scheme of Scinocca et al. (2000). This OGWD scheme employs two vertically propagating zero-phase-speed GWs to transport the horizontal momentum to the left and right of the resolved horizontal velocity vector at the launch layer, which extends from the surface to the height of the subgrid topography and the static stability. Functional dependence is on the near-surface wind speed, relative orientation of the subgrid topography (determining the orientation of the GW momentum flux) and the static stability in the source region. There are also two dimensionless parameters in the OGWD scheme allowing us to arbitrarily control the total value of launch momentum and the vertical flux of horizontal momentum (McLandress et al., 2013) indirectly also influencing the breaking level. The setting used in CMAM-sd has been tuned for polar-ozone chemistry studies in CMAM since it produces reasonable zonal-mean zonal winds and polar temperatures in the winter lower stratosphere (Scinocca et al., 2008). As the parameterized orographic GWs propagate upward they are subject to both critical-level filtering and nonlinear saturation (using a convective instability threshold), where the functional dependence is on the resolved horizontal wind speed and direction and static stability in the place (Scinocca et al., 2000).
The CMAM non-orographic GW parameterization scheme (Scinocca et al., 2008) is based on launching a globally uniform isotropic non-orographic GW spectrum in four cardinal horizontal directions at approximately 125 hPa. The aim is to produce a reasonable seasonal evolution of the zonal-mean zonal temperature and winds in the mesosphere. The zonal and meridional asymmetry stems from propagation effects only. For these reasons it is clear that the resulting non-orographic GWD (NOGWD) is not suitable for our analysis.
2.2 Multiple linear regression and other statistical methods
The specific GW responses to the changes in model atmospheric circulation can be fairly non-trivial, as their functional dependence on the background quantities is nonlinear and their extraction and quantification requires the application of statistical methods able to separate the effects of multiple simultaneously acting factors. Here, the association between OGWD and selected prominent climate variability modes has been investigated through multiple linear regression (MLR), using scalar indices of the NAO (defined as a normalized pressure difference between Reykjavík, Iceland, and Gibraltar), the Southern Oscillation (SO, defined as normalized pressure difference between Darwin, Australia, and Tahiti) and the QBO (defined as the zonal average of equatorial zonal wind at 30 hPa) as explanatory variables, along with descriptors of solar forcing (total solar irradiance), volcanic forcing (global mean stratospheric volcanic aerosol optical depth) and a linear approximation of the long-term trend component. The time series of the respective indices were used in the form available from the KNMI Climate explorer database (https://climexp.knmi.nl; last access: 29 October 2017). Additional experiments have also been carried out to investigate the effects of internal climate variability modes with dominant decadal and multi-decadal components: the Pacific Decadal Oscillation (PDO) and the Atlantic Multidecadal Oscillation (AMO). However, due to their largely statistically nonsignificant influence on GWD, as well as aliasing with other predictors (particularly the Southern Oscillation index), only results obtained without considering PDO and AMO are presented here. The statistical significance of the regression coefficients has been estimated by moving-block bootstrap, with the block size chosen to accommodate the autocorrelated structures in the regression residuals. MLR has also been used to assess the associations between GW effects and local circulation (characterized by geopotential height or wind speed at various pressure levels); the stepwise version of linear regression was used for some of these analysis setups, to identify the predictors most relevant to the OGWD output. Due to the distinct annual cycle of the activity of the orographic GWs (with their strongest manifestations typically observed during the cold part of the year), seasonal specifics need to be considered in the attribution analysis. While a sub-seasonal setup (such as an analysis carried out separately for individual months of the year) would be desirable, it would be difficult to achieve because of the relative shortness (a mere 32 years) of the time series analyzed here and the resulting limited amount of independent samples. For this reason, the separation into traditionally defined climatological seasons was used instead.
GW influence on the stratospheric circulation is often estimated and compared to forcing from resolved waves on the basis of zonal means (Albers and Birner, 2014). However, as we show in the first section of results, the CMAM-sd OGWD climatological horizontal distribution at 100, 50, 30 and 10 hPa is highly zonally asymmetric and OGWD tends to be distributed in local hotspots. The different dynamical effect of hotspots instead of zonally symmetric forces has been already shown numerically by Šácha et al. (2016). Results in the next sections illustrate that the studied atmospheric phenomena are connected with a different OGWD distribution and thus with a potentially different impact on the stratospheric dynamics.
Geller et al. (2013) made a first formal comparison between GW momentum fluxes from models and observations concluding that the geographical distribution of the fluxes from models and observations compares reasonably well, except for certain features connected mainly to non-orographic GWs. We are interested mainly in the geographical distribution, and so we simply compare the CMAM-sd OGWD hotspots with observed GW activity (not only momentum flux) hotspots at selected pressure levels in the stratosphere. The CMAM-sd momentum flux climatologies are shown in the Supplement.
3.1 CMAM-sd GWD climatology
First, we examine if the orographic GW parameterization scheme from CMAM-sd distributes the OGWD realistically. Figure 1 shows the OGWD climatology at 100, 50, 30 and 10 hPa levels. The 100 hPa level is traditionally below the level taken into account in the GW analyses from satellite observations (Alexander et al., 2010; Wright et al., 2016a; Šácha et al., 2015). At this level, in the DJF season, the OGWD is dominated by a Himalayan hotspot, which has not received significant attention in observational analyses yet (probably due to its emergence at rather lower levels). However, enhanced momentum fluxes have already been observed in this region, e.g., by Wright et al. (2016a). Another hotspot emerging in the Northern Hemisphere (NH) is connected with the Rocky Mountains. These hotspots are not visible at the higher levels. In the Southern Hemisphere (SH), during southern summer conditions, we see comparable magnitudes of OGWD (up to 20 m s−1 day−1) as for the NH connected with the southern tip of the Andes, Tasmania and New Zealand. Those high OGWD values in the summer hemisphere vanish at higher levels, which is in line with Baumgaertner and McDonald (2007), who attributed the small amount of summertime potential energy to lower-level critical filtering.
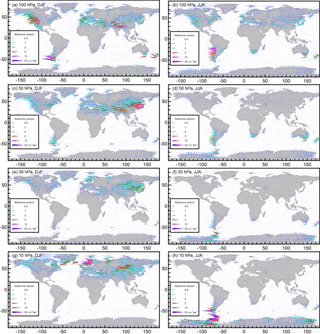
Figure 1Mean seasonal wind tendency due to OGWs (m s−1 day−1) at the 100 hPa (a, b), 50 hPa (c, d), 30 hPa (e, f) and 10 hPa (g, h) level, during DJF (a, c, e, g) and JJA (b, d, f, h) seasons.

Figure 2Standard deviation (SD) of the monthly series of wind tendency due to OGW (m s−1 day−1), displayed in a vector-like form and assigning the value for the eastward component to the x axis and value for the northward component to the y axis.
In the JJA season at 100 hPa, there is no dominant hotspot in the NH, while the SH OGWD distribution is dominated by the hotspot connected to the Andes. At 50 hPa in the DJF, there is a dominating hotspot in the region of eastern Asia corresponding to the eastern Asia/northern Pacific (EA/NP) hotspot observed by Šácha et al. (2015) or referred to as Mongolian orography in White et al. (2017, 2018). In the SH in the JJA season, the Andes are dominant, but note that the OGWD magnitude is smaller than for the EA/NP in the DJF season. Interestingly, at 30 hPa we see the dominance of the same hotspots as at 50 hPa but with a smaller magnitude of OGWD. In the SH in the JJA, the OGWD around the Drake Passage and Antarctic Peninsula (Hindley et al., 2015; Hoffmann et al., 2013, 2016; Wright et al., 2016b; de la Torre et al., 2012) begins to gain strength. At 10 hPa, in the NH in DJF, the Scandinavian hotspot starts to be dominant (Hoffmann et al., 2013; John and Kumar, 2012). In the SH in JJA, the southern Andes (Hoffmann et al., 2013; de la Torre et al., 2012), Drake Passage and Antarctic Peninsula hotspots dominate. Interestingly, we can also see moderately strong OGWD (Fig. 1c, 50 hPa, DJF) over small remote islands in the SH (Alexander and Grimsdell, 2013; Hoffmann et al., 2013). We conclude that the OGWD distribution from CMAM-sd gives a sufficiently realistic distribution of the OGWD for our analysis, given the assumptions employed in the parameterization and the lack of direct observational information on the OGWD and GWD in general.
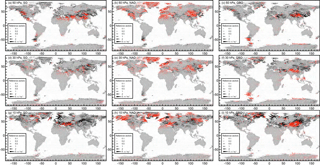
Figure 3Response of the OGWD (m s−1 day−1) at the 50 hPa (a, b, c), 30 hPa (d, e, f) and 10 hPa (g, h, i) level related to the activity of the Southern Oscillation (a, d, g), North Atlantic Oscillation (b, e, h) and quasi-biennial oscillation (c, f, i). The responses correspond to the increase in the oscillation index by four times its SD, i.e., to the transition of the respective oscillation from a highly negative to a highly positive phase; red symbols pertain to locations with at least one wind tendency component response statistically significant at the 95 % confidence level; bright red indicates at least one component significant at the 99 % confidence level. Analysis period: 1979–2010, monthly data, DJF season.
Figure 2 gives an illustration of how much the OGWD is changing on the interannual scale. Note that the arrows do not show the drag direction but illustrate a ratio of the meridional and zonal SD (both always positive). We see that at 10 hPa, large OGWD variations correspond to Scandinavia, central Asia and Greenland in the NH and the southern tip of the Andes together with the region of Antarctic Peninsula in the SH winter. standard deviation (SD) values reach 20 m s−1 day−1 in both hemispheres with a prevalence of the zonal OGWD component (except the Antarctic Peninsula). The OGWD variability at the 30 hPa level is dominated by the EA/NP and Scandinavian hotspots with maximum values of SD below 5 m s−1 day−1. This magnitude is reached only in the Antarctic Peninsula region in JJA in the SH. In the NH, the meridional component has relatively lower variability than at 10 hPa.
At 50 hPa in the NH winter, we see the largest OGWD variations in the EA/NP hotspot and surprisingly large values also locally in the SH in the southern Andes. This is also the only region with pronounced variation in OGWD in the SH winter. The Rocky Mountains and especially the Himalayas and southern Andes with SD values around 5 m s−1 day−1 dominate the 100 hPa level in DJF. At 100 hPa, the relative contribution of the meridional OGWD component variability is bigger than at 50 and 30 hPa. In SH in DJF and JJA, the variability in the Andes dominates.
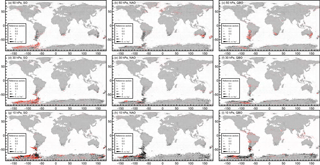
Figure 4Response of the OGWD (m s−1 day−1) at the 50 hPa (a, b, c), 30 hPa (d, e, f) and 10 hPa (g, h, i) level related to the activity of the Southern Oscillation (a, d, g), North Atlantic Oscillation (b, e, h) and quasi-biennial oscillation (c, f, i). The responses correspond to the increase in the oscillation index by 4 times its SD, i.e., to the transition of the respective oscillation from a highly negative to a highly positive phase; red symbols pertain to locations with at least one wind tendency component response statistically significant at the 95 % confidence level; bright red indicates at least one component significant at the 99 % confidence level. Analysis period: 1979–2010, monthly data, JJA season
Generally, the OGWD varies interannually by about half of the climatological OGWD magnitude (even reaching it at 10 hPa), with respective hotspots dominating the variability at the particular pressure levels of their climatological influence.
3.2 MLR results
Responses of the OGWD to the phase of major internal climate oscillations are shown at the 50, 30 and 10 hPa levels. In the NH in DJF, the variability connected with NAO dominates by far (Fig. 3, middle column) in the sense that it is distributed across the whole hemisphere with many significant regions and responses of up to 5 m s−1 day−1. As could be expected from the NAO definition, it is most pronounced in regions surrounding the North Atlantic. Note especially that at all analyzed isobaric levels, there is a dipole-like structure between Greenland and Scandinavia together with coastal areas in other places in western Europe. That indicates that during the positive NAO phase the GW activity suppresses the eastward wind above Greenland and enhances it above western Europe while the opposite is true of the negative phase. A similar dipole can be found at the western coast of North America, but only at the 50 hPa level. At higher levels, the signal above Alaska is more pronounced. The NAO signal is also pronounced in northeastern America, central Asia and partly in the EA/NP region (at 50 and 30 hPa levels) and in northern Asia for the 10 hPa level. There is also a significant signal exceeding 2 m s−1 day−1 in northern Africa for the 50 hPa level. The SO signal in the DJF season in the NH is mostly pronounced at 50 and 10 hPa level. At 50 hPa it constitutes a ring of significant OGWD responses higher than 2 m s−1 day−1, whereas at the 10 hPa level the signal in northeastern America, Turkey, Iran and the Caucasus region dominates. At 50 hPa there is also a strong localized signal in the southern tip of South America. The QBO signal in DJF is mostly pronounced in central Asia in the NH and southern Andes together with the Antarctic Peninsula at 50 and 30 hPa in the SH.
During austral winter (JJA; Fig. 4), the largest signal found in the OGWD belongs to the SO, with Antarctica dominating at the 50 hPa level. At higher levels there is a dipole-like feature between Antarctica and the southern tip of the Andes. There is also a strong (more than 2 m s−1 day−1) significant signal connected with the QBO at the 50 hPa level over the Andes. Somewhat surprisingly we can also find a significant NAO signal (ca. 1 m s−1 day−1) around southern Australia and New Zealand at 50 hPa. The results of the regression of solar activity and volcanic forcing were not shown because they gain a mostly insignificant OGWD signal. Only at 50 hPa is there a weak (up to 1 m s−1 day−1) significant solar signal in northeastern America and Antarctica in their respective winter periods.
To illustrate that it is necessary to consider geographical distribution for the analysis of the interannual variability in OGWD, we show the MLR results also for zonal means of OGWD (shown for DJF only). For the zonal OGWD component (Fig. 5), we can see that there is only a weak positive significant NAO signal at all levels and a very small positive significant SO signal at 50 hPa between 20–30∘ N corresponding to the belt described in the discussion of the Fig. 3. The magnitude of the detected signal is lower than 1 m s−1 day−1 everywhere. For the QBO and also for the meridional component (Fig. 6) of all indices, the signal is not significantly positive or negative or lower than 0.1 m s−1 day−1 almost anywhere. The situation is similar also for the JJA season (not shown).
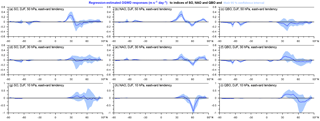
Figure 5Response of the zonal-mean OGWD (m s−1 day−1) at the 50 hPa (a, b, c), 30 hPa (d, e, f) and 10 hPa (g, h, i) level related to the activity of the Southern Oscillation (a, d, g), North Atlantic Oscillation (b, e, h) and quasi-biennial oscillation (c, f, i). The responses correspond to the increase in the oscillation index by 4 times its SD, i.e., to the transition of the respective oscillation from a highly negative to a highly positive phase; the blue curve shows the signal value and blue shading illustrates the 95 % confidence interval. Analysis period: 1979–2010, monthly data, DJF season.
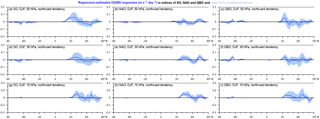
Figure 6Response of the meridional mean OGWD (m s−1 day−1) at the 50 hPa (a, b, c), 30 hPa (d, e, f) and 10 hPa (g, h, i) level related to the activity of the Southern Oscillation (a, d, g), North Atlantic Oscillation (b, e, h) and quasi-biennial oscillation (c, f, i). The responses correspond to the increase in the oscillation index by 4 times its SD, i.e., to the transition of the respective oscillation from a highly negative to a highly positive phase; the blue curve shows the signal value and blue shading illustrates the 95 % confidence interval. Analysis period: 1979–2010, monthly data, DJF season.
The general finding of the results presented above is that the OGWD varies locally by a few meters per second per day depending on the phase of the climate indices and also that the geographical variation in hotspots can vary from a phase to phase. The analysis also points to the important finding that the significant signal connected to the climate oscillations diminishes in the case of the traditional zonal-mean approach.
3.3 Explanatory factors
The results presented above alone cannot confirm our hypothesis on the tropospheric variability transfer to the stratosphere by altering the GW activity and its distribution because the MLR results do not illustrate the causality of the problem considered. It can be argued that the OGWD variability results are caused simply by the variations in the stratosphere or upper troposphere (e.g., jet shift, meandering due to anomalous planetary wave (PW) activity) possibly leading to Doppler shifting effects or variations in critical lines for the orographic GW propagation (Pisoft et al., 2018). The modulation of GWs by PWs receives great attention in the scientific community (Cullens et al., 2015), and considering this causality mechanism, the dynamical influence of the OGWD variations would be of secondary importance only. Therefore, in this subsection we analyze the daily data of wind direction and speed (the influence of another OGWD parameterization variable – a stability – was not diagnosed) to show that at least a part of the OGWD variability is directly influenced by the variability at the surface or in the lower troposphere.
Figures 7, 8 and 9 present an analysis of daily data aimed at estimating how much of the OGWD variability at a given level can be explained by 850 hPa wind variance. At 50 hPa, we can see that the link between the lower-tropospheric winds and OGWD is strongly expressed in a belt in the midlatitudes and tropics of the NH. The fraction of variance explained is maximal and the geographical distribution is also very similar for the links between zonal wind/the zonal OGWD component and meridional wind/the meridional OGWD component. In the regions with significant orography and particularly in the region of the EA/NP hotspot (which dominates the OGWD field at 50 hPa in the NH), the majority of OGWD variance is explained by lower-tropospheric winds.
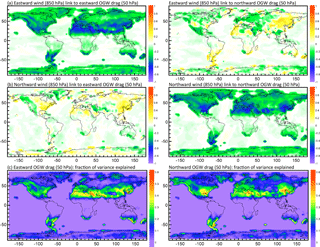
Figure 7(a, b) Standardized regression coefficients between orographic gravity wave drag at the 50 hPa level (predictand) and eastward and northward wind components at the 850 hPa level (predictors), during the DJF season. (c) Coefficient of determination, i.e., the fraction of total variance of OGWD explained through the regression mappings by both components of wind at the 850 hPa level. Analysis period: 1979–2010, daily data, DJF season.

Figure 8(a, b) Standardized regression coefficients between orographic gravity wave drag at the 30 hPa level (predictand) and eastward and northward wind components at the 850 hPa level (predictors), during the DJF season. (c) Coefficient of determination, i.e., the fraction of total variance of OGWD explained through the regression mappings by both components of wind at the 850 hPa level. Analysis period: 1979–2010, daily data, DJF season.

Figure 9(a, b) Standardized regression coefficients between orographic gravity wave drag at the 10 hPa level (predictand) and eastward and northward wind components at the 850 hPa level (predictors), during the DJF season. (c) Coefficient of determination, i.e., the fraction of total variance of OGWD explained through the regression mappings by both components of wind at the 850 hPa level. Analysis period: 1979–2010, daily data, DJF season.
An interesting pattern can be seen in the SH around the Andes, where the maximum of the OGWD variance explained is located up- and downwind from the Andes. Also interestingly, at 50 hPa, in the southern Andes/Antarctic Peninsula region, a larger fraction of the meridional OGWD component variance is explained by surface conditions than for the zonal component. Otherwise, the fraction of the OGWD variability explained in the Australian/New Zealand hotspot (connected in previous analyses mainly with the NAO signal) is about two-fifths of the total variance.
At the 30 hPa level the fraction of variance explained is lower – around one-third of the variance in eastern Asia and locally in northern Atlantic coastal regions and in the SH. In the eastern Asia region this is due to the stratospheric background affecting the critical line occurrence and propagation of the GWs between 50 and 30 hPa. Interestingly, for the meridional OGWD component, the fraction of variance explained is slightly higher. At the 10 hPa level, there is a single maximum of explained total variance (around one-third) in Scandinavia. A similar amount of variance is also explained by 850 hPa winds for Iceland but for the zonal OGWD component only.
Another approach allowing us to assess the variability in the orographic GW sourcing is to analyze the 850 hPa orographic GW fluxes as a proxy and apply the MLR method. However, with this method it is not possible to link the results directly with the variability in the OGWD because processes like the Doppler shifting of amplitudes or critical line variations can alter the resulting OGWD significantly. Also note, that this analysis is made with monthly data and the comparability with previous analyses is limited.
In Fig. 10 we see that in the NH in DJF there is a strong signal in Greenland and western Europe connected with the NAO and an equally strong signal in GW sourcing variability in central Asia (Himalayas), Greenland, Iceland and Svalbard connected with the QBO. The SO signal is largely insignificant in the NH, but in the SH in JJA it is most strongly pronounced mainly in the southern tip of the Andes and Antarctic Peninsula. In the SH in JJA, some regions of significant signal in GW sourcing variability connected with the NAO (the Andes, Australia and New Zealand) and QBO (Antarctica) can also be found.
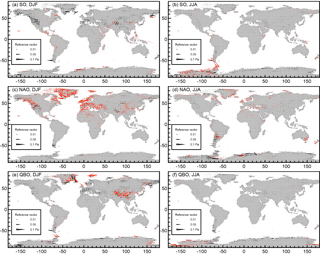
Figure 10Response of the orographic GW momentum fluxes (Pa) at the 850 hPa level related to the activity of the Southern Oscillation (a, b), North Atlantic Oscillation (c, d) and quasi-biennial oscillation (e, f) during DJF (a, c, e) and JJA (b, d, f) seasons. The responses correspond to the increase in the oscillation index by 4 times its SD, i.e., to the transition of the respective oscillation from a highly negative to a highly positive phase; red symbols pertain to locations with at least one orographic GW flux component response statistically significant at the 95 % confidence interval. Analysis period: 1979–2010, monthly data.
Although the strong QBO signal may be surprising, the QBO phase exhibits a distinct and in some regions statistically significant influence on the lower-tropospheric winds in CMAM-sd (not shown). The influence of the QBO on the surface meteorological conditions has been pointed out in the literature in detail before (Hansen et al., 2016; Marshall and Scaife, 2009).
The study presented here introduces an analysis of interannual variability in the CMAM-sd OGWD at particular pressure levels in the stratosphere. Building on the results of Šácha et al. (2016), the aim of our paper has been to evaluate if the tropospheric variability can affect the OGWD distribution in the stratosphere.
In the first section we show the simulated climatological OGWD distribution at 100, 50, 30 and 10 hPa levels and estimate its interannual variability to be about half of the climatological OGWD value at the major hotspots. The main conclusion of this part is that the distribution can be regarded as reasonably realistic because the main GW activity hotspots are detected in a similar way to that described in the GW-observing literature (also considering the practically missing observational constraints on the OGWD in general). In the second section, results of the MLR analysis of monthly OGWD data are presented showing a significant NAO, SO and QBO signal of a few (up to 5) m s−1 day−1 in the OGWD at 50, 30 and 10 hPa. Depending on the phase of the climate oscillations, OGWD values in the hotspot regions and also the distribution of OGWD hotspots vary interannually on the selected pressure levels. However, in the case of the traditional zonal-mean analysis, the detected signal is small and mostly insignificant. In the last part we demonstrate that a large fraction (over hotspots like EA/NP) of the described OGWD variance can be linked to the variance of 850 hPa winds. We also find significant NAO, SO and QBO signals in the orographic GW momentum fluxes at 850 hPa suggesting different orographic GW sourcing in a model depending on the phase of these phenomena.
For the CMAM-sd simulation, all of the results support the original hypothesis of the tropospheric variability transfer into the stratosphere via OGWD variability. The suggested mechanism depicts a simplified picture, not taking into account the inner variability in the stratosphere, PW propagation or mutual interactions between the troposphere and stratosphere. On the other hand, it has to be noted that the GWs are arguably the fastest way for communicating information in the vertical (apart from the acoustic and acoustic gravity waves with effects much higher in the middle and in the upper atmosphere). Therefore, tropospheric information can be quickly mediated into the stratosphere and OGWD variability can be directly influenced by the variability at the surface or in the lower troposphere. During propagation and in the stratosphere, those fast and GW-mediated tropospheric contributions interact nonlinearly with the stratospheric processes (Doppler shifting, critical-level variations). However, it makes little sense to look for the causality between GWs and PWs (background field for GWs) when only the steady state (monthly data) is considered.
There is also a factor of longitudinal variability in the OGWD (and GWD in general). For the PW breaking there is almost no information in the literature about the geometry and longitudinal variability in the imposed drag force. But for the GWs, it has been shown in Šácha et al. (2016) that localized forces can lead to dynamical responses different from the reactions to a zonally averaged forcing. Although the gravity waves are a small-scale phenomenon, they are often organized in large-scale hotspots constituting a large-scale forcing. We argue that incorporating these effects into related analyses can open new horizons for research on teleconnections between tropospheric (e.g., SO, NAO or PDO) and stratospheric (e.g., polar vortex stability) phenomena. The magnitude of the OGWD variations reaching a few meters per second per day locally can significantly affect the stratospheric dynamics. It was shown by Šácha et al. (2016) that the injection of a localized versus zonally symmetric GWD of 10 m s−1 day−1 can lead to wind speed differences of an order of 10 m s−1 at corresponding vertical levels. For the residual circulation and Eliassen–Palm flux the localized GW forcing of this magnitude induced differences ranging up to 50 % of their climatological values in the middle and upper atmosphere mechanistic model (Pogoreltsev et al., 2007) used for the study Šácha et al. (2016).
Our analysis relies on parameterized processes, and thus the results can be highly model dependent considering that other models use different OGWD parameterizations than CMAM. The NOGWD in CMAM-sd at the vertical domain of our analysis is clearly underestimated compared to the current consensus on the GW distribution and impacts on the stratosphere (Hoffmann et al., 2013; Holt et al., 2017; Polichtchouk et al., 2007). It would be highly interesting to look at NOGWD variations connected with variability in jets, fronts, etc., in future research. For the real atmosphere our results strongly suggest that GWs can play a much bigger and different role in the troposphere–stratosphere coupling and in shaping the stratospheric dynamics than is currently acknowledged. However, at the current stage it is impossible to evaluate the actual details of the connection between climate oscillations (tropospheric variability) and OGWD changes. This is partly due to the nudging procedure, which prevents us from analyzing the GWD impact on the circulation because this impact is weakened by the relaxation towards ERA-I data. However, as we have only analyzed the OGWD interannual variability, the nudging is very advantageous for us (compared to a free running model), since the distribution of gravity wave momentum fluxes in CMAM-sd can resemble the distribution of real fluxes (McLandress et al., 2013).
From a methodological point of view we must also note that GWs and their effects are handicapped by the use of monthly mean data because the GWs are very intermittent in the atmosphere (Hertzog et al., 2012; Wright and Gille, 2013), and also in CMAM, the OGWD shows large daily (and shorter, not shown) variability. Therefore, for example, the monthly mean values may be hiding 1 order stronger intermittent drag values. During the analysis, there were also indications of noteworthy deviations from linear behavior in some regions, encouraging future transition to nonlinear regression techniques.
In our future work, we aim to separate and estimate the dynamical impacts of the different OGWD distributions belonging to the respective phases of the NAO, SO and QBO by producing sensitivity simulations with a mechanistic model with prescribed OGWD values and a distribution according to MLR results from CMAM.
CMAM outputs are available upon registration at the website of the Canadian Centre for Climate Modelling and Analysis: http://climate-modelling.canada.ca/climatemodeldata/cmam, last access: 29 October 2017.
The supplement related to this article is available online at: https://doi.org/10.5194/esd-9-647-2018-supplement.
The authors declare that they have no conflicts of interest.
The work presented here would not have been possible without the utilized CMAM
datasets from the Canadian Centre for Climate Modelling and
Analysis. This study was supported by GA CR under grant
nos. 16-01562J and 18-01625S. In later stages of the manuscript
preparation, Petr Šácha was supported by the Government of Spain
under grant no. CGL2015-71575-P. Petr Šácha thanks
Juan Añel
and Laura de la Torre for fruitful discussions. We thank our colleague
Ales Kuchar for his assistance with data preparation. We also thank
the two anonymous reviewers whose insightful and constructive
comments helped to improve and clarify this paper.
Edited by: Zhenghui Xie
Reviewed by: two anonymous referees
Albers, J. R. and Birner, T.: Vortex preconditioning due to planetary and gravity waves prior to sudden stratospheric warmings, J. Atmos. Sci., 71, 4028–4054, https://doi.org/10.1175/JAS-D-14-0026.1, 2014. a
Alexander, M. J. and Grimsdell, A. W.: Seasonal cycle of orographic gravity wave occurrence above small islands in the Southern Hemisphere: Implications for effects on the general circulation, J. Geophys. Res.-Atmos., 118, 589–599, https://doi.org/10.1002/2013JD020526, 2013. a
Alexander, S. P. and Sato, K.: Gravity wave dynamics and climate: An update from the SPARC gravity wave activity, SPARC Newsletter, 44, 9–13, 2015. a
Alexander, S. P. and Shepherd, M. G.: Planetary wave activity in the polar lower stratosphere, Atmos. Chem. Phys., 10, 707–718, https://doi.org/10.5194/acp-10-707-2010, 2010. a
Alexander, S. P., Klekociuk, A. R., and Tsuda, T.: Gravity wave and orographic wave activity observed around the antarctic and arctic stratospheric vortices by the cosmic gps-ro satellite constellation, J. Geophys. Res.-Atmos., 114, D17103, https://doi.org/10.1029/2009JD011851, 2009. a
Alexander, M. J., Geller, M., McLandress, C., Polavarapu, S., Preusse, P., Sassi, F., Sato, K., Eckermann, S., Ern, M., Hertzog, A., Kawatani, Y., Pulido, M., Shaw, T. A., Sigmond, M., Vincent, R., and Watanabe, S.: Recent developments in gravity-wave effects in climate models and the global distribution of gravity-wave momentum flux from observations and models, Q. J. Roy. Meteor. Soc., 136, 1103–1124, https://doi.org/10.1002/qj.637, 2010. a
Añel, J. A.: The stratosphere: history and future a century after its discovery, Contemp. Phys., 57, 230–233, https://doi.org/10.1080/00107514.2015.1029521, 2016. a
Baumgaertner, A. J. G. and McDonald, A. J.: A gravity wave climatology for antarctica compiled from challenging minisatellite payload/global positioning system (champ/gps) radio occultations, J. Geophys. Res.-Atmos., 112, D05103, https://doi.org/10.1029/2006JD007504, 2007. a
Calvo, N., Polvani, L. M, and Solomon, S.: On the surface impact of arctic stratospheric ozone extremes, Environ. Res. Lett., 10, 094003, https://doi.org/10.7916/D8HD7VHJ, 2015. a
Cullens, C. Y., England, S. L., and Immel, T. J.: Global responses of gravity waves to planetary waves during stratospheric sudden warming observed by saber, J. Geophys. Res.-Atmos., 120, 12018–12026, https://doi.org/10.1002/2015JD023966, 2015. a
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The era-interim reanalysis: configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011. a
de la Torre, A., Alexander, P., Hierro, R., Llamedo, P., Rolla, A., Schmidt, T., and Wickert, J.: Large-amplitude gravity waves above the southern andes, the drake passage, and the antarctic peninsula, J. Geophys. Res.-Atmos., 117, D02106, https://doi.org/10.1029/2011JD016377, 2012. a, b
Ern, M., Preusse, P., Gille, J. C., Hepplewhite, C. L., Mlynczak, M. G., Russell, J. M., and Riese, M.: Implications for atmospheric dynamics derived from global observations of gravity wave momentum flux in stratosphere and mesosphere, J. Geophys. Res.-Atmos., 116, D19107, https://doi.org/10.1029/2011JD015821, 2011. a
Fritts, D. C., Smith, R. B., Taylor, M. J., Doyle, J. D., Eckermann, S. D., Dörnbrack, A., Rapp, M., Williams, B. P., Pautet, P., Bossert, K., Criddle, N. R., Reynolds, C. A., Reinecke, P. A., Uddstrom, M., Revell, M. J., Turner, R., Kaifler, B., Wagner, J. S., Mixa, T., Kruse, C. G., Nugent, A. D., Watson, C. D., Gisinger, S., Smith, S. M., Lieberman, R. S., Laughman, B., Moore, J. J., Brown, W. O., Haggerty, J. A., Rockwell, A., Stossmeister, G. J., Williams, S. F., Hernandez, G., Murphy, D. J., Klekociuk, A. R., Reid, I. M., and Ma, J.: The Deep Propagating Gravity Wave Experiment (DEEPWAVE): An airborne and ground-based exploration of gravity wave propagation and effects from their sources throughout the lower and middle atmosphere, B. Am. Meteorol. Soc., 97, 425–453, https://doi.org/10.1175/BAMS-D-14-00269.1, 2016. a
Geller, M., Alexander, M. J., Love, P. T., Bacmeister, J., Ern, M., Hertzog, A., Manzini, E., Preusse, P., Sato, K., Scaife, A., and Zhou, T. H.: A comparison between gravity wave momentum fluxes in observations and climate models, J. Climate, 26, 6383–6405, https://doi.org/10.1175/JCLI-D-12-00545.1, 2013. a, b
Hansen, F., Matthes, K., and Wahl, S.: Tropospheric qbo–enso interactions and differences between the atlantic and pacific, J. Climate, 29, 1353–1368, https://doi.org/10.1175/JCLI-D-15-0164.1, 2016. a
Hertzog, A., Alexander, M. J., and Plougonven, R.: On the intermittency of gravity wave momentum flux in the stratosphere, J. Atmos. Sci., 69, 3433–3448, https://doi.org/10.1175/JAS-D-12-09.1, 2012. a
Hindley, N. P., Wright, C. J., Smith, N. D., and Mitchell, N. J.: The southern stratospheric gravity wave hot spot: individual waves and their momentum fluxes measured by COSMIC GPS-RO, Atmos. Chem. Phys., 15, 7797–7818, https://doi.org/10.5194/acp-15-7797-2015, 2015. a
Hoffmann, L., Xue, X., and Alexander, M. J.: A global view of stratospheric gravity wave hotspots located with Atmospheric Infrared Sounder observations, J. Geophys. Res.-Atmos., 118, 416–434, https://doi.org/10.1029/2012JD018658, 2013. a, b, c, d, e
Hoffmann, L., Grimsdell, A. W., and Alexander, M. J.: Stratospheric gravity waves at Southern Hemisphere orographic hotspots: 2003–2014 AIRS/Aqua observations, Atmos. Chem. Phys., 16, 9381–9397, https://doi.org/10.5194/acp-16-9381-2016, 2016. a
Holt, L. A., Alexander, M. J., Coy, L., Liu, C., Molod, A., and Pawson, S.: An evaluation of gravity waves and gravity wave sources in the Southern Hemisphere in a 7 km global climate simulation, Q. J. Roy. Meteor. Soc., 143, 2481–2495, https://doi.org/10.1002/qj.3101, 2017. a
John, S. R. and Kumar, K. K.: Timed/saber observations of global gravity wave climatology and their interannual variability from stratosphere to mesosphere lower thermosphere, Clim. Dynam., 39, 1489–1505, https://doi.org/10.1007/s00382-012-1329-9, 2012. a
Kalisch, S., Preusse, P., Ern, M., Eckermann, S. D., and Riese, M.: Differences in gravity wave drag between realistic oblique and assumed vertical propagation, J. Geophys. Res.-Atmos., 119, 10081–10099, https://doi.org/10.1002/2014JD021779, 2014. a, b
Lawrence, B. N.: The Effect of Parameterized Gravity Wave Drag on Simulations of the Middle Atmosphere during Northern Winter 1991/1992 – General Evolution, Springer, Berlin, Heidelberg, 291–307, https://doi.org/10.1007/978-3-642-60654-0_20, 1997. a
Manzini, E., Karpechko, A. Y., Anstey, J., Baldwin, M. P., Black, R. X., Cagnazzo, C., Calvo, N., Charlton-Perez, A., Christiansen, B., Davini, P., Gerber, E., Giorgetta, M., Gray, L., Hardiman, S. C., Lee, Y.-Y., Marsh, D. R., McDaniel, B. A., Purich, A., Scaife, A. A., Shindell, D., Son, S.-W., Watanabe, S., and Zappa, G.: Northern winter climate change: Assessment of uncertainty in cmip5 projections related to stratosphere-troposphere coupling, J. Geophys. Res.-Atmos., 119, 7979–7998, https://doi.org/10.1002/2013JD021403, 2014. a
Marshall, A. G. and Scaife, A. A.: Impact of the qbo on surface winterclimate, J. Geophys. Res.-Atmos., 114, D18110, https://doi.org/10.1029/2009JD011737, 2009. a
McFarlane, N. A.: The effect of orographically excited gravity wave drag on the general circulation of the lower stratosphere and troposphere, J. Atmos. Sci., 44, 1775–1800, https://doi.org/10.1175/1520-0469(1987)044<1775:TEOOEG>2.0.CO;2, 1987. a
McLandress, C., Scinocca, J. F., Shepherd, T. G., Reader, M. C., and Manney, G. L.: Dynamical control of the mesosphere by orographic and nonorographic gravity wave drag during the extended northern winters of 2006 and 2009, J. Atmos. Sci., 70, 2152–2169, https://doi.org/10.1175/JAS-D-12-0297.1, 2013. a, b, c
Pawson, S.: Effects of Gravity Wave Drag in the Berlin Troposphere-Stratosphere-Mesosphere GCM, Springer, Berlin, Heidelberg, 327–336, https://doi.org/10.1007/978-3-642-60654-0_22, 1997. a
Pisoft, P., Šácha, P., Miksovsky, J., Huszar, P., Scherllin-Pirscher, B., and Foelsche, U.: Revisiting internal gravity waves analysis using GPS RO density profiles: comparison with temperature profiles and application for wave field stability study, Atmos. Meas. Tech., 11, 515–527, https://doi.org/10.5194/amt-11-515-2018, 2018. a
Plougonven, R. and Zhang, F.: Internal gravity waves from atmospheric jets and fronts, Rev. Geophys., 52, 33–76, https://doi.org/10.1002/2012RG000419, 2014. a
Pogoreltsev, A. I., Vlasov, A. A., Fröhlich, K., and Jacobi, C.: Planetary waves in coupling the lower and upper atmosphere, J. Atmos. Sol.-Terr. Phy., 69, 2083–2101, https://doi.org/10.1016/j.jastp.2007.05.014, 2007. a
Polichtchouk, I., Shepherd, T. G., Hogan, R. J., and Bechtold, P.: Sensitivity of the Brewer-Dobson circulation and polar vortex variability to parametrized nonorographic gravity-wave drag in a high-resolution atmospheric model, J. Atmos. Sci., 75, 1525–1543, https://doi.org/10.1175/JAS-D-17-0304.1, 2018. a
Šácha, P., Kuchař, A., Jacobi, C., and Pišoft, P.: Enhanced internal gravity wave activity and breaking over the northeastern Pacific–eastern Asian region, Atmos. Chem. Phys., 15, 13097–13112, https://doi.org/10.5194/acp-15-13097-2015, 2015. a, b
Šácha, P., Lilienthal, F., Jacobi, C., and Pišoft, P.: Influence of the spatial distribution of gravity wave activity on the middle atmospheric dynamics, Atmos. Chem. Phys., 16, 15755–15775, https://doi.org/10.5194/acp-16-15755-2016, 2016. a, b, c, d, e, f, g, h
Sandu, I., Bechtold, P., Beljaars, A., Bozzo, A., Pithan, F., Shepherd, T. G., and Zadra, A.: Impacts of parameterized orographic drag on the northern hemisphere winter circulation, J. Adv. Model. Earth Sy., 8, 196–211, https://doi.org/10.1002/2015MS000564, 2016. a
Scinocca, J. F.: An accurate spectral nonorographic gravity wave drag parameterization for general circulation models, J. Atmos. Sci., 60, 667–682, https://doi.org/10.1175/1520-0469(2003)060<0667:AASNGW>2.0.CO;2, 2003. a
Scinocca, J. F. and McFarlane, N. A.: The parametrization of drag induced by stratified flow over anisotropic orography, Q. J. Roy. Meteor. Soc., 126, 2353–2393, https://doi.org/10.1002/qj.49712656802, 2000. a, b
Scinocca, J. F., McFarlane, N. A., Lazare, M., Li, J., and Plummer, D.: Technical Note: The CCCma third generation AGCM and its extension into the middle atmosphere, Atmos. Chem. Phys., 8, 7055–7074, https://doi.org/10.5194/acp-8-7055-2008, 2008. a, b
White, R. H., Battisti, D. S., and Roe, G. H.: Mongolian mountains matter most: Impacts of the latitude and height of asian orography on pacific wintertime atmospheric circulation, J. Climate, 30, 4065–4082, https://doi.org/10.1175/JCLI-D-16-0401.1, 2017. a, b, c
White, R. H., Battisti, D. S., and Sheshadri, A.: Orography and the boreal winter stratosphere: The importance of the Mongolian mountains, Geophys. Res. Lett., 45, 2088–2096, https://doi.org/10.1002/2018GL077098, 2018. a, b
Wright, C. J. and Gille, J. C.: Detecting overlapping gravity waves using the s-transform, Geophys. Res. Lett., 40, 1850–1855, https://doi.org/10.1002/grl.50378, 2013. a
Wright, C. J., Hindley, N. P., and Mitchell, N. J.: Combining airs and mls observations for three-dimensional gravity wave measurement, Geophys. Res. Lett., 43, 884–893, https://doi.org/10.1002/2015GL067233, 2016a. a, b
Wright, C. J., Hindley, N. P., Moss, A. C., and Mitchell, N. J.: Multi-instrument gravity-wave measurements over Tierra del Fuego and the Drake Passage – Part 1: Potential energies and vertical wavelengths from AIRS, COSMIC, HIRDLS, MLS-Aura, SAAMER, SABER and radiosondes, Atmos. Meas. Tech., 9, 877–908, https://doi.org/10.5194/amt-9-877-2016, 2016b. a





