the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Reliability ensemble averaging of 21st century projections of terrestrial net primary productivity reduces global and regional uncertainties
Jean-François Exbrayat
A. Anthony Bloom
Pete Falloon
Akihiko Ito
T. Luke Smallman
Mathew Williams
Multi-model averaging techniques provide opportunities to extract additional information from large ensembles of simulations. In particular, present-day model skill can be used to evaluate their potential performance in future climate simulations. Multi-model averaging methods have been used extensively in climate and hydrological sciences, but they have not been used to constrain projected plant productivity responses to climate change, which is a major uncertainty in Earth system modelling. Here, we use three global observationally orientated estimates of current net primary productivity (NPP) to perform a reliability ensemble averaging (REA) method using 30 global simulations of the 21st century change in NPP based on the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP) ”business as usual” emissions scenario. We find that the three REA methods support an increase in global NPP by the end of the 21st century (2095–2099) compared to 2001–2005, which is 2–3 % stronger than the ensemble ISIMIP mean value of 24.2 Pg C y−1. Using REA also leads to a 45–68 % reduction in the global uncertainty of 21st century NPP projection, which strengthens confidence in the resilience of the CO2 fertilization effect to climate change. This reduction in uncertainty is especially clear for boreal ecosystems although it may be an artefact due to the lack of representation of nutrient limitations on NPP in most models. Conversely, the large uncertainty that remains on the sign of the response of NPP in semi-arid regions points to the need for better observations and model development in these regions.
- Article
(3326 KB) - Full-text XML
-
Supplement
(6787 KB) - BibTeX
- EndNote
Anthropogenic emissions of carbon dioxide (CO2) enhance the uptake of atmospheric carbon by terrestrial ecosystems through net primary productivity (NPP). This so-called CO2 fertilization effect has helped offset 25–30 % of CO2 emissions responsible for climate change in recent decades (Canadell et al., 2007; Le Quéré et al., 2009). There exists a large uncertainty as to whether this positive effect of CO2 fertilization will be resilient to climate change, as shown by the spread between model projections from various intercomparison projects (Friedlingstein et al., 2006; Arora et al., 2013; Friend et al., 2014; Nishina et al., 2014, 2015), especially in highly productive tropical regions (Rammig et al., 2010; Cox et al., 2013). However, large ensembles of projections are challenging to interpret as they may include models with an opposite response to the same change in boundary conditions (Friedlingstein et al., 2006). Simulations from the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP; Warszawski et al., 2014) have shown that most of the uncertainty in 21st century projections of the terrestrial carbon cycle can be attributed to differences among global vegetation models (GVMs; Friend et al., 2014; Nishina et al., 2014, 2015), although a non-negligible part of the uncertainty arises from differences in climate projections themselves (Ahlström et al., 2012).
In recent years multi-model averaging has been widely used to extract information from large ensembles of simulations in studies targeting climate change (Bishop and Abramowitz, 2012; Krishnamurti et al., 1999), rainfall–runoff processes (Georgakakos et al., 2004; Huisman et al., 2009; Shamseldin et al., 1997; Viney et al., 2009) and catchment-scale nutrient exports (Exbrayat et al., 2010, 2013b). These methods range from simple arithmetic means of model ensembles to more elaborate weighting schemes such as Bayesian that take model performance into account model averaging (Raftery et al., 2005). The underlying assumption is that a model that is better able to reproduce current conditions should be given more weight in the final projection than a poorly performing model. The more complex reliability ensemble averaging (REA; Giorgi and Mearns, 2002) approach takes into account a measure of convergence between projections to identify the most likely change: this way, the REA method avoids giving too much weight to an overfitted model that may accurately represent current conditions for the wrong reasons but predicts vastly different change than other ensemble members (Exbrayat et al., 2013b). Metrics measuring model independence (Bishop and Abramowitz, 2012) have also been introduced in weighting schemes to avoid pseudo-replication.
Until recently, applying these advanced multi-model averaging methods to simulations of the global carbon cycle has remained a challenge because of the lack of global observational datasets to constrain, for example the REA weighting scheme. Schwalm et al. (2015) have presented results of skill-based model averaging applied to an ensemble of 10 models from the Multi-scale synthesis and Terrestrial Model Intercomparison Project (MsTMIP; Huntzinger et al., 2013). This pixel-wise approach assigned weights to historical simulations based on their ability to simulate gross primary productivity and biomass stocks but did not consider future projections. Lovenduski and Bonan (2017) considered a single value of cumulative terrestrial carbon uptake for 1959–2005 to derive one global coefficient per model to produce new projections. However, we are not aware of any studies using these methods in the context of spatially-explicit projections of the terrestrial carbon cycle under climate change.
Here, we present the first example of a pixel-wise application of the REA approach to extract a best estimate of NPP change (ΔNPP) during the 21st century under a ”business as usual” scenario of emissions from a large ensemble of projections. We perform the REA procedure three times using different observationally constrained estimates of current NPP: retrievals of the terrestrial carbon cycle with the CARbon DAta Model fraMework (CARDAMOM; Bloom et al., 2016) model–data fusion approach (Bloom and Williams, 2015a; Bloom et al., 2016), an approximation of NPP based on the up-scaled FLUXCOM gross primary productivity (GPP) datasets Jung et al., 2009, 2011, 2017; Tramontana et al., 2016) and the MOD17A3 MODIS NPP product (Running et al., 2004; Zhao et al., 2005; Zhao and Running, 2010). Based on optimally weighted model averages, we evaluate the impact of the REA method on 21st century projections of ΔNPP but also on the uncertainty in the future resilience of the CO2 fertilization that exists among the models. We show that the REA procedure can help identify regions where uncertainties remain large and thereby inform the future development of models and observational networks needed to improve climate change projections.
2.1 The ISIMIP ensemble
We used an ensemble of simulations of NPP from the ISIMIP. The ISIMIP simulations included here consist of six global vegetation models (GVM): HYBRID (Friend and White, 2000), JeDi (Pavlick et al., 2013), JULES (Clark et al., 2011), LPJmL (Sitch et al., 2003), SDGVM (Woodward et al., 1995) and VISIT (Ito and Inatomi, 2012). Each of these six GVMs was driven by bias-corrected output (Hempel et al., 2013) from five general circulation models (GCM): GFDL-ESM2M (Dunne et al., 2012), HadGEM2-ES (Collins et al., 2011), IPSL-CM5A-LR (Dufresne et al., 2013), MIROC-ESM-CHEM (Watanabe et al., 2011) and NorESM1-M (Bentsen et al., 2013), generating a total of 30 global simulations of NPP for the historical period and under the Representative Concentration Pathway 8.5 (RCP8.5). We chose the ISIMIP ensemble over other initiatives like C4MIP (Friedlingstein et al., 2006) or CMIP5 (Taylor et al., 2012) because the combination of multiple GVMs with multiple GCMs in ISIMIP allows a more comprehensive coverage of the uncertainty in the terrestrial carbon cycle and attribution of dominant factor in the uncertainty of the future (Friend et al., 2014; Nishina et al., 2014, 2015), although we note that these simulations omit feedbacks from the biosphere on weather and atmospheric CO2 concentrations. As the ensemble integrates five representations of the same GVM, and six representations of the same GCM, we avoid issues related to model genealogy (Knutti et al., 2013) that could lead similar models to bias results of the averaging because of intrinsic lack of independence between the different ensemble members (Bishop and Abramowitz, 2012). We focus our approach on NPP projections under the RCP8.5 scenario of emissions for which more simulations were available (Nishina et al., 2015). Mean annual current NPP and projected changes are summarized in Table 1 and Supplement Fig. S1. We note a large spread in current global NPP simulated by the models from 51.7 to 77.8 Pg C y−1 during 2001–2005, the last 5 years of the historical simulations, as well as ΔNPP in the last 5 years of the projections (2095–2099) ranging from −3.7 to 41.6 Pg C y−1. Further information on the models and the ISIMIP protocol can be found in the Supplement of Friend et al. (2014) and the respective model description papers listed in Table 1.
2.2 Benchmark datasets of modern NPP
We use three different estimates of current NPP: (a) an observationally bound terrestrial carbon cycle analysis estimate, (b) an estimate based on up-scaled eddy-covariance CO2 flux measurements and (c) an estimate based on satellite measurements of absorbed photosynthetically active radiation. To harmonize the approach, we re-gridded all observationally constrained NPP datasets to the lowest dataset resolution () and confined our analysis to the overlap period 2001–2005 for which benchmark datasets and ISIMIP models were available. Mean annual NPP and variability for each dataset is presented in Figs. S2 and S3.
2.2.1 CARDAMOM retrievals
CARDAMOM produces spatially explicit retrievals of the global terrestrial carbon cycle following a model–data fusion procedure. In each pixel, the Data Assimilation Linked Ecosystem Carbon version 2 (DALEC2; Bloom and Williams, 2015a; Williams et al., 2005) is driven by ERA-Interim reanalysis climate data (Dee et al., 2011) and burned area from the Global Fire Emission Database version 4 (Giglio et al., 2013). A Bayesian Markov chain Monte Carlo approach is implemented to constrain DALEC2 according to observations of MODIS leaf area index (Myneni et al., 2002), tropical biomass (Saatchi et al., 2011), soil carbon content from the Harmonized World Soil Database (HWSD; FAO, 2012) and a set of ecological and dynamic constraints (Bloom and Williams, 2015a). Through this Bayesian procedure, CARDAMOM provides an explicit estimation of the uncertainty in model parameters, and hence in land-atmosphere carbon fluxes such as NPP from site to global-scale (Bloom et al., 2016; Smallman et al., 2017). However, as not all the other datasets (see Sects. 2.2.2 and 2.2.3) provide a measure of the parametric uncertainty, in this study we rely on CARDAMOM's highest confidence estimates of a mean annual NPP of 49.9 Pg C y−1. More details on the framework can be found in the Supplement of Bloom et al. (2016).
2.2.2 FLUXCOM
The FLUXCOM project uses machine-learning methods (Tramontana et al., 2016) to up-scale global datasets from eddy-covariance measurements of CO2 and energy fluxes from the FLUXNET network (Baldocchi et al., 2001). In a first step, a machine-learning algorithm is used to extract a relationship between local environmental drivers and ecosystem fluxes (Jung et al., 2009). Then, the trained algorithm is used in combination with gridded climate data and remote sensing observations to produce a global estimate of monthly ecosystem fluxes at a spatial resolution. In its first dataset, FLUXCOM products relied on a random forest method (Breiman, 2001) but newly available datasets have been produced using additional machine-learning methods (Tramontana et al., 2016; Jung et al., 2017).
Here, we use the average of an ensemble of six FLUXCOM GPP datasets to derive an estimate of annual NPP for 2001–2005. These datasets were created using three machine-learning methods: random forest, artificial neural networks and multivariate regression splines. Each machine-learning method was used to produce two GPP datasets corresponding to two partitioning methods of net ecosystem exchange (see Reichstein et al., 2005 and Lasslop et al., 2009). Then, we used CARDAMOM's retrievals of carbon use efficiency (Bloom et al., 2016), the ratio of NPP to GPP, to derive a current value of NPP of 52.7 Pg C y−1 for the first 5 years of the 21st century from the 126.9 Pg C y−1 FLUXCOM-estimated GPP.
2.2.3 MODIS NPP
The MOD17 MODIS GPP/NPP dataset provides 8-day estimates of GPP and annual NPP at a 1 km spatial resolution since the year 2000. Therefore, GPP is calculated as the product of the amount of absorbed photosynthetically active radiation (estimated from the MOD15 MODIS LAI/FPAR product; Myneni et al., 2002) and a biome-specific radiation use efficiency that is adjusted as a function of air temperature and vapour pressure deficit. Land cover classification is derived from MODIS using the MCD12Q1 product (Friedl et al., 2002) while meteorological data are taken from the National Centers for Environmental Prediction (NCEP)/Department of Energy (DOE) Reanalyses II. Then, annual maintenance respiration is estimated using a temperature-acclimated Q10 relationship (Tjoelker et al., 2001) while growth respiration is assumed to be a fixed fraction of NPP. The MODIS NPP dataset has been used to quantify the impact of droughts (Zhao and Running et al., 2010) and the El Niño–Southern Oscillation on global terrestrial ecosystem productivity (Bastos et al., 2013). We re-gridded the annual NPP data to a spatial resolution for the reference years 2001–2005 from which we derived a 53.4 Pg C y−1 mean annual value.
2.3 Reliability ensemble averaging
The REA method was developed to assign coefficients to models in the context of future projections. In addition to using a measure of model performance to reproduce historical conditions, the REA weighting scheme implements a measure of model convergence to penalize models that do not predict the same response to changes (Exbrayat et al., 2013b).
In each pixel, each model projection i of the 30 GVM–GCM ensemble is assigned a reliability factor Ri that is calculated such as
where ε represents the variability in observations expressed as the difference between the largest and smallest values of annual NPP in each pixel (Fig. S3; Giorgi and Mearns, 2002), while Bi and Di correspond to a measure of model i's performance and convergence, respectively. The performance coefficient RB,i ranges from 0, for a poorly performing model, to 1 if the absolute value of Bi is smaller than the variability ε. Similarly, the convergence coefficient RD,i ranges from 0 for outlier projections to 1 if the absolute value of Di, the difference between the projection and the REA mean, is smaller than ε. As a result, the final model weight Ri also considers values ranging from 0 (excluded) to 1 (included). We produce three REA estimates based on CARDAMOM, FLUXCOM and MODIS NPP, further referred to as REAC, REAF and REAM, respectively. For each REA application, terms ε, Bi, Di, and hence Ri (Eq. 1) are recalculated based on the particular observational dataset to produce three independent sets of model coefficients.
Here, we apply the REA method to the ensemble of 30 ISIMIP simulations of 21st century ΔNPP under the RCP8.5 emission scenario. We first re-gridded the ISIMIP data using the ”remapcon” function of the Climate Data Operators version 1.6.9 to match the spatial resolution of the observationally constrained datasets (see Sect. 2.2) and performed the procedure in each land pixel to create maps of REA averages. We then apply the REA method three times (REAC, REAF and REAM) to evaluate the current performance of the ISIMIP simulations of NPP.
For each 30 simulations of the ISIMIP ensemble, we calculated Bi in each pixel as
where NPPi is the mean annual NPP predicted by model i during the last 5 years of the historical simulations and NPPobs corresponds to either of the observational datasets' mean annual NPP. Then for each model the value of Di was calculated in each pixel as the difference between the change predicted by model i and the REA average as
where ΔNPPi is the change in mean NPP in the last 5 years of the RCP8.5 simulation (2095–2099) compared to the last five years of the historical simulations (2001–2005) predicted by the ensemble member i, and N is the total number of ensemble members. The REA average is not known beforehand and weights RD,i are calculated iteratively (Giorgi and Mearns, 2002).
The uncertainty around the REA average change is calculated as the weighted root-mean square difference (RMSD) calculated following
where ΔNPPREA is the REA average change. Assuming that the error distribution is somewhere between uniform and Gaussian, the 60–70 % confidence interval of the REA is represented by ΔNPPREA±RMSD (Giorgi and Mearns, 2002).
Giorgi and Mearns (2002) further introduced a quantitative measure of the collective model reliability ρ, based on Ri, where
which will vary pixel-wise based on each model's performance with respect to the mean and variability represented in each observational dataset as well as the convergence to the REA average. The reliability measure ρ can be further decomposed in ρB and ρD, as
where ρB and ρD correspond to the ensemble reliability with respect to model biases and model convergence, respectively. ρ, ρB and ρD all take values ranging from 0, indicating a lack of agreement between models, to 1, indicating a consensus between models in terms of performance and projected changes.
The REA method yields a global increase in NPP of 24.6±8.5 Pg C y−1 (REA average ± RMSD) using CARDAMOM in REAC, 24.8±9.5 Pg C y−1 using FLUXCOM in REAF and 25.0±14.4 Pg C y−1 using MODIS NPP in REAM. As the ISIMIP ensemble mean indicated a ΔNPP of 24.2 Pg C y−1, these results represent a ∼2 % increase in the mean for both REAC and REAF and 3 % for REAM. The pixel-wise 1 SD uncertainty in the ISIMIP ensemble was 26.3 Pg C y−1 and the REA results indicate strong reduction of 68 % for REAC, 64 % for REAF and 45 % for REAM. These results further indicate that in all three cases, the REA method reduces the uncertainty of the ensemble spread toward an agreement on a future increase in the global land carbon uptake.
Zonal means (Fig. 1) indicate that the ISIMIP ensemble mean and all three REAC, REAF and REAM averages estimate an increase in NPP across all latitudes. All three REA averages predict a weaker increase in NPP at high latitudes of the Northern Hemisphere and Southern Hemisphere. They also agree on a stronger increase in NPP than the ISIMIP ensemble mean for tropical regions between 15∘ S and 10∘ N but also between 20 and 25∘ N and temperate regions around 55 to 65∘ N. REAC and REAF indicate a weaker increase in NPP than ISIMIP around 20∘ S while the REAM average is similar to the ISIMIP ensemble mean in these regions. The uncertainty around each of the REA averages is smaller than the uncertainty around the ISIMIP ensemble mean across all latitudinal zones. Furthermore, while the very large uncertainty around the ISIMIP ensemble mean does not provide confidence on the sign of ΔNPP across most regions, the uncertainty around all three REA averages is constrained toward an increase in NPP across all regions, except around 20∘ S.
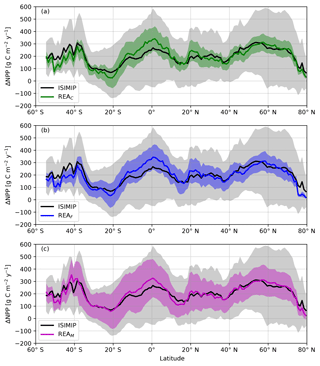
Figure 1Zonal mean ΔNPP by the end of the 21st century (averaged over 2095–2099) under RCP8.5 compared to the end of the historical simulations (averaged over 2001–2005). Shading represents the uncertainty around the zonal mean across the ISIMIP ensemble, taken as 1 SD for ISIMIP, and calculated following Eq. (4) for REA. REAC, REAF and REAM refer to REA values calculated based on observationally constrained CARDAMOM, FLUXCOM and MODIS NPP, respectively.
The spatial distribution of the ISIMIP ensemble mean ΔNPP contrasts with that of the three REA averages with noticeable differences across all regions of the globe (Fig. 2). All three REA averages predict a weaker increase in NPP than the ISIMIP ensemble in Canada and Scandinavia, while they predict a stronger increase in NPP in Eurasia. Similarly, all three REA averages predict a stronger increase in NPP than the ISIMIP ensemble in the tropical rainforests of South America, Africa and Southeast Asia. The REA averages agree on a weaker ΔNPP in semi-arid regions of the Sahel, southern Africa, Australia and the Tibetan Plateau. Overall, the REAC, REAF and REAM values exhibit broadly similar patterns in the spatial distribution of ΔNPP differences with the ISIMIP ensemble mean that are confirmed by Pearson's correlation coefficient of 0.63, between REAC and REAF, 0.61 between REAC and REAM, and 0.68 between REAF and REAM.
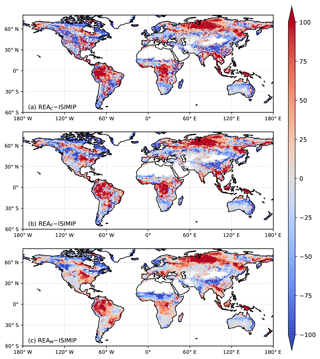
Figure 2Differences between ΔNPP in 2095–2099 compared to 2001–2005 from the REA average and ISIMIP ensemble mean (). Red indicates where the REA averages predict ΔNPP greater than the ISIMIP ensemble mean. Blue indicates where the REA averages predict ΔNPP less than the ISIMIP ensemble mean.
The uncertainty in ΔNPP is reduced across most regions of the globe for REAC, REAF and REAM (Figs. 1 and 3). This reduction of uncertainty leads to a confidence on the sign estimation of ΔNPP in 86, 80 and 76 % of all the land pixels for REAC, REAF and REAM, respectively, compared with 43 % for the ISIMIP ensemble. The average reduction in uncertainty is large in regions north of 40∘ N (Fig. 1), mostly corresponding to a reduction in uncertainty in boreal Eurasia (Fig. 3) that provides better confidence in an increase in NPP (Fig. 2). We note that the uncertainty in the REAM remains similar to the uncertainty around the ISIMIP ensemble mean for large portions of the Southern Hemisphere such as southern Africa. However, all three REAC, REAF and REAM cannot provide confidence on the sign of ΔNPP for southern Africa and Australia.
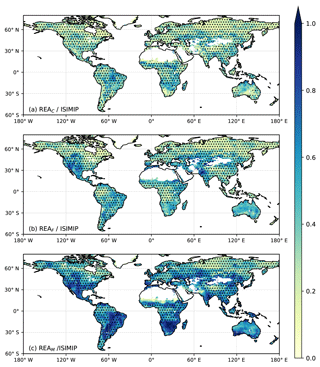
Figure 3Ratio of the uncertainty in 21st century ΔNPP from each REA average to the uncertainty in the ISIMIP ensemble. For ISIMIP, the uncertainty is calculated as the SD across the ensemble while the uncertainty around the REA averages is calculated following Eq. (4). Stippling indicates regions where there is an agreement on the sign of ΔNPP through the uncertainty.
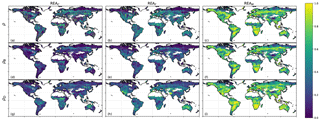
The zonal means of the mean values of the three coefficients Ri, RB,i and RD,i (Fig. 4) show that a MODIS-based REAM yields larger values of all coefficients compared to REAC and REAF. We note strong inter-model similarities in the spatial distribution of model weights (Ri; Fig. 4a–c), biases (RB,i; Fig. 4d–f) and convergence of the projected ΔNPP (RD,i; Fig. 4g–i). Only the HYBRID models are almost systematically assigned lower Ri values as a result of lower values for both RB,i (i.e. a larger bias than the other models) and RD,i (i.e. a divergence in projected ΔNPP). This is especially obvious in boreal regions north of 60∘ N where HYBRID is assigned values significantly closer to 0 in REAC, REAF and REAM.
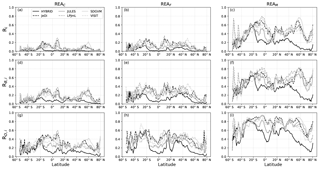
Figure 4Zonal mean Ri, RB,i and RD,i (row-wise) in each REAC, REAF and REAM (column-wise). Each line represents the average value obtained across the five simulations of each GVM.
The collective model reliability measure ρ provides a quantification of the spread of model weights determined through the REA method (Fig. 5). Regions where ρ is close to 1 show a strong consensus between models on the current NPP and on 21st century ΔNPP. There are large differences in ρ depending on the NPP observational datasets used to constrain the REA (Fig. 5). Indeed, while the average value of ρ is 0.29 for REAC and 0.32 for REAF, it is 0.62 for REAM. REAC and REAF yield very low values of ρ in boreal regions (Fig. 5) while REAM leads to values of ρ close to 1 in many regions south of 60∘ S. The measure of reliability ρ can be further decomposed into two components ρB and ρD (Fig. 5d–i, Eqs. 6 and 7). Results indicate that ρD is consistently greater than ρB for REAC, REAF and REAM. This result means that model convergence in the simulation of ΔNPP is greater than the model ability in reproducing current NPP. In other words, the model performance evaluated against the three current NPP datasets contributes the most to decreasing the ensemble reliability ρ. Values of ρB are lower than 0.10 in boreal regions for REAC and REAF, indicating that model bias is greater than the variability in NPP ε estimated from the CARDAMOM retrievals and the FLUXCOM-based NPP by a factor of 10. Conversely, regions where ρB is close to 1 for REAM indicate that the variability in the MODIS NPP observations is larger than model biases.
The globally integrated values of the REA average change (24.6 to 25.0 Pg C y−1) and the ISIMIP ensemble mean (24.2 Pg C y−1) are similar. This is in agreement with a previous multi-model approach that only found a 0.01 Pg C y−1 difference in the historical mean annual net ecosystem exchange between a simple mean and a weighted average based on model performance (Schwalm et al., 2015). However, in contrast to this previous study, we find that in REAC, REAF and REAM a large spatial variability in grid cell differences (Fig. 2) that compensate for each other to yield a relatively small global difference with the ISIMIP ensemble mean. The three REA averages indicate a stronger positive ΔNPP than the ISIMIP ensemble mean for boreal Eurasia and tropical rainforests (Figs. 1 and 2) and a weaker but still positive ΔNPP in northern Canada and semi-arid regions like the Sahel, the Tibetan Plateau, southern Africa and Australia.
The reduction in uncertainty arising from the REA method helps put a greater confidence in a sustained CO2 fertilization effect throughout the 21st century, although these results may be influenced by model-wise differences in process representation. In both the ISIMIP ensemble mean and the three REA averages, NPP increases at high latitudes where nitrogen (N) limitation on NPP dominates (Zhang et al., 2011; Exbrayat et al., 2013a) but is only represented in the HYBRID and SDGVM models (Table 1; Nishina et al., 2014). The increase in NPP in these N-limited regions is in contrast with observations in Free-Air CO2 Enrichment experiments that indicate a quick weakening of the CO2 fertilization effect as soil N stores deplete (Norby et al., 2010). Models which integrate coupled C–N cycles generally predict the historical land carbon sink in good agreement with estimates from the Global Carbon Project (Huntzinger et al., 2017) and project a decrease in NPP throughout the 21st century (Thornton et al., 2009; Goll et al., 2012; Zhang et al., 2013; Wieder et al., 2015).
Similarly, recent observations have concluded a total absence of CO2 fertilization effect under phosphorus-limited conditions (Ellsworth et al., 2017) which dominate in the tropics and lead to an additional reduction of NPP in model projections (Goll et al., 2012; Zhang et al., 2013; Wieder et al., 2015). Here, only the HYBRID and SDGVM models integrate the representation of N limitations on NPP (Nishina et al., 2014) and none of them represent phosphorous limitations. HYBRID is also the only model to predict a possible decrease in global NPP throughout the 21st century (Table 1 and Friend et al., 2014) because of a reduction in global NPP at high latitudes and in tropical rainforests (Supplement Fig. S1). Thus, HYBRID is assigned low RD,i weights in these regions (Fig. 4g–i and Supplement Figs. S4–12) and cannot influence the REA average and the calculation of its uncertainty (Eq. 4) despite integrating a more detailed representation of ecosystem processes. However, HYBRID also exhibits stronger differences from the observational datasets than the other models, especially at high latitudes (Fig. 4d–f), which may indicate a strong sensitivity to N limitations. Nevertheless, we note that all models' performances tend to decrease in regions north of 60∘ N where their ΔNPP projections also diverge (Figs. 4d–f and 5d–f).
Overall, the promising REA results should be used carefully as they cannot correct for the omission of key processes by a large fraction of the ensemble members. Like in previous multi-model averaging studies focused on the carbon cycle (e.g. Schwalm et al., 2015; Lovenduski and Bonan, 2017) or climate (Krishnamurti et al., 1999; Giorgi and Mearns, 2002), we used available simulations in a post-processing procedure. We note, however, that the ratio of two out of six models including carbon–nutrient interactions in the ISIMIP ensemble is commensurate to other model inter-comparison projects: 3 out of 10 CMIP5 models (Exbrayat et al., 2014) or 2 out of 8 models in the new ISIMIP experiments presented by Chen et al. (2017). There is also considerable debate on how good large-scale NPP observational products are (Smith et al., 2015; de Kauwe et al., 2016), a problem that we address by performing the REA approach three times.
In all three REAC, REAF and REAM cases, the global uncertainty around the REA average is reduced compared to the uncertainty within the ISIMIP ensemble, which provides a higher degree of confidence in the resilience of the global CO2 fertilization effect to warming. The reduction in uncertainty and the gain in confidence on the sign of ΔNPP, is especially obvious in boreal regions for all three REA cases (Fig. 3). Conversely, uncertainties on the sign of ΔNPP remain large for all REA cases in semi-arid regions of southern Africa and Australia. It is a non-trivial result as the response of these ecosystems to climate events like El Niño and La Niña drives the inter-annual variability and the trend of the global terrestrial carbon sink (Bastos et al., 2013; Poulter et al., 2014; Ahlström et al., 2015), while projections indicate a gain of forest ecosystems over savannahs in the future (Moncrieff et al., 2016).
Because of the way the REA method assigns coefficients to ensemble members with respect to the annual variability in the data ε (Eq. 1), the final REA average and uncertainty are conditional on the variability represented in the current estimate of NPP. Figure 5, sections a–c show that the reliability of the ensemble measured by ρ varies depending on which observational dataset is used, although generally lower values of ρB and ρD at high latitudes indicate that models disagree on the current NPP and future ΔNPP in these regions. Furthermore, high values of ρ for REAM indicate a larger variability ε in the MODIS dataset compared to CARDAMOM and the FLUXCOM-based NPP data (Fig. S3). This larger variability leads to more models being given a weight close to 1 in the averaging scheme because the variability is larger than their bias (Fig. 5f) or the predicted change (Fig. 5i). Conversely, the relatively smaller variability in CARDAMOM retrievals leads more models to be weighted poorly according to both their performance (Fig. 5d) and their convergence with other models (Fig. 5g). The variability ε influences the final uncertainty and as a result the REAC has a smaller uncertainty because it is more penalizing on models, and vice versa with MODIS NPP.
We applied the REA method on a pixel-by-pixel basis to an ensemble of 30 simulations of historical and 21st century NPP from the ISIMIP project. Our results indicate that using either CARDAMOM retrievals, a FLUXCOM based estimate of current NPP or data from MODIS to constrain the REA scheme helps by halving the uncertainty in 21st century global ΔNPP. This process leads to a higher confidence in a sustained CO2 fertilization effect. We nevertheless note that a large uncertainty remains in semi-arid regions that is mostly attributable to differences in process representation in global vegetation models. Furthermore, most models used here do not account for N limitations on NPP and this may have altered the outcome of the convergence coefficient used in REA.
CARDAMOM output used in this study is available from Bloom and Williams (2015b) from the University of Edinburgh's DataShare service at https://doi.org/10.7488/ds/316. FLUXCOM GPP estimates used in this study are available from the data portal of the Max Planck Institute for Biogeochemistry at https://doi.org/10.17871/FLUXCOM_RS_METEO_CRUNCEPv6_1980_2013_v1 (Jung, 2016). The MODIS MOD17 NPP product is available from the website of the Numerical Terradynamic Simulation Group at the University of Montana (http://files.ntsg.umt.edu/data/NTSG_Products/MOD17/GeoTIFF/MOD17A3/; Zhao et al., 2005; Zhao and Running, 2010). REA output (Exbrayat and Williams, 2018) is available from the University of Edinburgh's DataShare service at https://doi.org/10.7488/ds/2304.
The supplement related to this article is available online at: https://doi.org/10.5194/esd-9-153-2018-supplement.
The authors declare that they have no conflict of interest.
This work was supported by the Natural Environment Research
Council through the National Centre for Earth Observation. Part of this work
was carried out at the Jet Propulsion Laboratory, California Institute of
Technology, under a contract with the National Aeronautics and Space
Administration: Anthony Bloom was supported by NASA Earth Sciences grant
(no. NNH16ZDA001N-IDS). Pete Falloon was supported by the Joint UK DECC/Defra
MetOffice Hadley Centre Climate Programme (GA01101). For their roles in
producing, coordinating, and making available the ISIMIP model output, we
acknowledge the modelling groups and the ISIMIP coordination
team.
Edited by: Somnath Baidya
Roy
Reviewed by: two anonymous referees
Ahlström, A., Schurgers, G., Arneth, A., and Smith, B.: Robustness and uncertainty in terrestrial ecosystem carbon response to CMIP5 climate change projections, Environ. Res. Lett., 7, 044008, https://doi.org/10.1088/1748-9326/7/4/044008, 2012.
Ahlström, A., Raupach, M. R., Schurgers, G., Smith, B., Arneth, A., Jung, M., Reichstein, M., Canadell, J. G., Friedlingstein, P., Jain, A. K., Kato, E., Poulter, B., Sitch, S., Stocker, B. D., Viovy, N., Wang, Y. P., Wiltshire, A., Zaehle, S., and Zeng, N.: Carbon cycle. The dominant role of semi-arid ecosystems in the trend and variability of the land CO2 sink, Science, 348, 895–899, https://doi.org/10.1126/science.aaa1668, 2015.
Arora, V. K., Boer, G. J., Friedlingstein, P., Eby, M., Jones, C. D., Christian, J. R., Bonan, G., Bopp, L., Brovkin, V., Cadule, P., Hajima, T., Ilyina, T., Lindsay, K., Tjiputra, J. F., and Wu, T.: Carbon–concentration and carbon–climate feedbacks in CMIP5 earth system models, J. Climate, 26, 5289–5314, https://doi.org/10.1175/JCLI-D-12-00494.1, 2013.
Baldocchi, D., Falge, E., Gu, L. H., Olson, R., Hollinger, D., Running, S., Anthoni, P., Bernhofer, C., Davis, K., Evans, R., Fuentes, J., Goldstein, A., Katul, G., Law, B., Lee, X. H., Malhi, Y., Meyers, T., Munger, W., Oechel, W., U, Paw, K. T., Pilegaard, K., Schmid, H. P., Valentini, R., Verma, S., Vesala, T., Wilson, K., and Wofsy, S.: FLUXNET: a new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities, B. Am. Meteorol. Soc., 82, 2415–2434, https://doi.org/10.1175/1520-0477(2001)082<2415:fantts>2.3.co;2, 2001.
Bastos, A., Running, S. W., Gouveia, C., and Trigo, R. M.: The global NPP dependence on ENSO: La Niña and the extraordinary year of 2011, J. Geophys. Res.-Biogeo., 118, 1247–1255, https://doi.org/10.1002/jgrg.20100, 2013.
Bentsen, M., Bethke, I., Debernard, J. B., Iversen, T., Kirkevåg, A., Seland, Ø., Drange, H., Roelandt, C., Seierstad, I. A., Hoose, C., and Kristjánsson, J. E.: The Norwegian Earth System Model, NorESM1-M – Part 1: Description and basic evaluation of the physical climate, Geosci. Model Dev., 6, 687–720, https://doi.org/10.5194/gmd-6-687-2013, 2013.
Bishop, C. H. and Abramowitz, G.: Climate model dependence and the replicate Earth paradigm, Clim. Dynam., 41, 885–900, https://doi.org/10.1007/s00382-012-1610-y, 2012.
Bloom, A. A. and Williams, M.: Constraining ecosystem carbon dynamics in a data-limited world: integrating ecological ”common sense” in a model–data fusion framework, Biogeosciences, 12, 1299–1315, https://doi.org/10.5194/bg-12-1299-2015, 2015a.
Bloom, A. and Williams, M.: CARDAMOM 2001–2010 global carbon Model–Data Fusion (MDF) analysis, 2001–2010, [dataset], University of Edinburgh, School of GeoSciences, available at: https://doi.org/10.7488/ds/316 (last access: 17 November 2016), 2015b.
Bloom, A. A., Exbrayat, J.-F., van der Velde, I. R., Feng, L., and Williams, M.: The decadal state of the terrestrial carbon cycle: global retrievals of terrestrial carbon allocation, pools, and residence times., P. Natl. Acad. Sci. USA, 113, 1285–1290, https://doi.org/10.1073/pnas.1515160113, 2016.
Breiman, L.: Random forests, Mach. Learn., 45, 5–32, 2001.
Canadell, J. G., Le Quéré, C., Raupach, M. R., Field, C. B., Buitenhuis, E. T., Ciais, P., Conway, T. J., Gillett, N. P., Houghton, R. A., and Marland, G.: Contributions to accelerating atmospheric CO2 growth from economic activity, carbon intensity, and efficiency of natural sinks, P. Natl. Acad. Sci. USA, 104, 18866–18870, https://doi.org/10.1073/pnas.0702737104, 2007.
Chen, M., Rafique, R., Asrar, G. R., Bond-Lamberty, B., Ciais, P., Zhao, F., Reyer, C. P. O., Ostberg, S., Chang, J., Ito, A., Yang, J., Zeng, N., Kalnay, E., West, T., Leng, G., Francois, L., Munhoven, G., Henrot, A., Tian, H., Pan, S., Nishina, K., Viovy, N., Morfopoulos, C., Betts, R., Schaphoff, S., Steinkamp, J., and Hickler, T.: Regional contribution to variability and trends of global gross primary productivity, Environ. Res. Lett., 12, 105005, https://doi.org/10.1088/1748-9326/aa8978, 2017.
Clark, D. B., Mercado, L. M., Sitch, S., Jones, C. D., Gedney, N., Best, M. J., Pryor, M., Rooney, G. G., Essery, R. L. H., Blyth, E., Boucher, O., Harding, R. J., Huntingford, C., and Cox, P. M.: The Joint UK Land Environment Simulator (JULES), model description – Part 2: Carbon fluxes and vegetation dynamics, Geosci. Model Dev., 4, 701–722, https://doi.org/10.5194/gmd-4-701-2011, 2011.
Collins, W. J., Bellouin, N., Doutriaux-Boucher, M., Gedney, N., Halloran, P., Hinton, T., Hughes, J., Jones, C. D., Joshi, M., Liddicoat, S., Martin, G., O'Connor, F., Rae, J., Senior, C., Sitch, S., Totterdell, I., Wiltshire, A., and Woodward, S.: Development and evaluation of an Earth-System model – HadGEM2, Geosci. Model Dev., 4, 1051–1075, https://doi.org/10.5194/gmd-4-1051-2011, 2011.
Cox, P. M., Pearson, D., Booth, B. B., Friedlingstein, P., Huntingford, C., Jones, C. D., and Luke, C. M.: Sensitivity of tropical carbon to climate change constrained by carbon dioxide variability, Nature, 494, 341–344, https://doi.org/10.1038/nature11882, 2013.
De Kauwe, M. G., Keenan, T. F., Medlyn, B. E., Prentice, I. C., and Terrer., C.: Satellite based estimates underestimate the effect of CO2 fertilization on net primary productivity, Nat. Clim. Change, 6, 892–893, https://doi.org/10.1038/nclimate3105, 2016.
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim reanalysis: configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011.
Dufresne, J.-L., Foujols, M.-A., Denvil, S., Caubel, A., Marti, O., Aumont, O., Balkanski, Y., Bekki, S., Bellenger, H., Benshila, R., Bony, S., Bopp, L., Braconnot, P., Brockmann, P., Cadule, P., Cheruy, F., Codron, F., Cozic, A., Cugnet, D., Noblet, N., Duvel, J.-P., Ethé, C., Fairhead, L., Fichefet, T., Flavoni, S., Friedlingstein, P., Grandpeix, J.-Y., Guez, L., Guilyardi, E., Hauglustaine, D., Hourdin, F., Idelkadi, A., Ghattas, J., Joussaume, S., Kageyama, M., Krinner, G., Labetoulle, S., Lahellec, A., Lefebvre, M.-P., Lefevre, F., Levy, C., Li, Z. X., Lloyd, J., Lott, F., Madec, G., Mancip, M., Marchand, M., Masson, S., Meurdesoif, Y., Mignot, J., Musat, I., Parouty, S., Polcher, J., Rio, C., Schulz, M., Swingedouw, D., Szopa, S., Talandier, C., Terray, P., Viovy, N. and Vuichard, N.: Climate change projections using the IPSL-CM5 Earth System Model: from CMIP3 to CMIP5, Clim. Dynam., 40, 2123–2165, https://doi.org/10.1007/s00382-012-1636-1, 2013.
Dunne, J. P., John, J. G., Adcroft, A. J., Griffies, S. M., Hallberg, R. W., Shevliakova, E., Stouffer, R. J., Cooke, W., Dunne, K. A., Harrison, M. J., Krasting, J. P., Malyshev, S. L., Milly, P. C. D., Phillipps, P. J., Sentman, L. T., Samuels, B. L., Spelman, M. J., Winton, M., Wittenberg, A. T., and Zadeh, N.: GFDL's ESM2 global coupled climate–carbon earth system models. Part I: Physical formulation and baseline simulation characteristics, J. Climate, 25, 6646–6665, https://doi.org/10.1175/JCLI-D-11-00560.1, 2012.
Ellsworth, D. S., Anderson, I. C., Crous, K. Y., Cooke, J., Drake, J. E., Gherlenda, A. N., Gimeno, T. E., Macdonald, C. A., Medlyn, B. E., Powell, J. R., Tjoelker, M. G., and Reich, P. B.: Elevated CO2 does not increase eucalypt forest productivity on a low-phosphorus soil, Nat. Clim. Change, 7, 279–282, https://doi.org/10.1038/nclimate3235, 2017.
Exbrayat, J.-F., Viney, N. R., Seibert, J., Wrede, S., Frede, H.-G., and Breuer, L.: Ensemble modelling of nitrogen fluxes: data fusion for a Swedish meso-scale catchment, Hydrol. Earth Syst. Sci., 14, 2383–2397, https://doi.org/10.5194/hess-14-2383-2010, 2010.
Exbrayat, J.-F., Pitman, A. J., Zhang, Q., Abramowitz, G., and Wang, Y.-P.: Examining soil carbon uncertainty in a global model: response of microbial decomposition to temperature, moisture and nutrient limitation, Biogeosciences, 10, 7095–7108, https://doi.org/10.5194/bg-10-7095-2013, 2013a.
Exbrayat, J.-F., Viney, N. R., Frede, H.-G., and Breuer, L.: Using multi-model averaging to improve the reliability of catchment scale nitrogen predictions, Geosci. Model Dev., 6, 117–125, https://doi.org/10.5194/gmd-6-117-2013, 2013b.
Exbrayat, J.-F., Pitman, A. J., and Abramowitz, G.: Response of microbial decomposition to spin-up explains CMIP5 soil carbon range until 2100, Geosci. Model Dev., 7, 2683–2692, https://doi.org/10.5194/gmd-7-2683-2014, 2014.
Exbrayat, J.-F. and Williams, M.: Reliability Ensemble Averaging of ISIMIP NPP projections for 2095–2099 under RCP8.5, [dataset], School of GeoSciences, University of Edinburgh, available at: https://doi.org/10.7488/ds/2304, last access: 19 February 2018.
FAO/IIASA/ISRIC/ISSCAS/JRC: Harmonized World Soil Database (version 1.21), FAO, Rome, Italy and IIASA, Laxenburg, Austria, 2012.
Friedl, M. A., McIver, D. K., Hodges, J. C. F., Zhang, X. Y., Muchoney, D., Strahler, A. H., Woodcock, C. E., Gopal, S., Schneider, A., Cooper, A., Baccini, A., Gao, F., and Schaaf, C.: Global land cover mapping from MODIS: algorithms and early results, Remote Sens. Environ., 83, 287–302, https://doi.org/10.1016/S0034-4257(02)00078-0, 2002.
Friedlingstein, P., Cox, P., Betts, R., Bopp, L., von Bloh, W., Brovkin, V., Cadule, P., Doney, S., Eby, M., Fung, I., Bala, G., John, J., Jones, C., Joos, F., Kato, T., Kawamiya, M., Knorr, W., Lindsay, K., Matthews, H. D., Raddatz, T., Rayner, P., Reick, C., Roeckner, E., Schnitzler, K.-G., Schnur, R., Strassmann, K., Weaver, A. J., Yoshikawa, C., and Zeng, N.: Climate–carbon cycle feedback analysis: results from the C4MIP Model intercomparison, J. Climate, 19, 3337–3353, https://doi.org/10.1175/JCLI3800.1, 2006.
Friend, A. D. and White, A.: Evaluation and analysis of a dynamic terrestrial ecosystem model under preindustrial conditions at the global scale, Global Biogeochem. Cy., 14, 1173–1190, https://doi.org/10.1029/1999GB900085, 2000.
Friend, A. D., Lucht, W., Rademacher, T. T., Keribin, R., Betts, R., Cadule, P., Ciais, P., Clark, D. B., Dankers, R., Falloon, P. D., Ito, A., Kahana, R., Kleidon, A., Lomas, M. R., Nishina, K., Ostberg, S., Pavlick, R., Peylin, P., Schaphoff, S., Vuichard, N., Warszawski, L., Wiltshire, A., and Woodward, F. I.: Carbon residence time dominates uncertainty in terrestrial vegetation responses to future climate and atmospheric CO2, P. Natl. Acad. Sci. USA, 111, 3280–3285, https://doi.org/10.1073/pnas.1222477110, 2014.
Georgakakos, K. P., Seo, D.-J., Gupta, H., Schaake, J., and Butts, M. B.: Towards the characterization of streamflow simulation uncertainty through multimodel ensembles, J. Hydrol., 298, 222–241, https://doi.org/10.1016/j.jhydrol.2004.03.037, 2004.
Giglio, L., Randerson, J. T., and van der Werf, G. R.: Analysis of daily, monthly, and annual burned area using the fourth-generation global fire emissions database (GFED4), J. Geophys. Res.-Biogeo., 118, 317–328, https://doi.org/10.1002/jgrg.20042, 2013.
Giorgi, F. and Mearns, L. O.: Calculation of average, uncertainty range, and reliability of regional climate changes from AOGCM simulations via the “Reliability Ensemble Averaging” (REA) method, J. Climate, 15, 1141–1158, https://doi.org/10.1175/1520-0442(2002)015<1141:COAURA>2.0.CO;2, 2002.
Goll, D. S., Brovkin, V., Parida, B. R., Reick, C. H., Kattge, J., Reich, P. B., van Bodegom, P. M., and Niinemets, Ü.: Nutrient limitation reduces land carbon uptake in simulations with a model of combined carbon, nitrogen and phosphorus cycling, Biogeosciences, 9, 3547–3569, https://doi.org/10.5194/bg-9-3547-2012, 2012.
Hempel, S., Frieler, K., Warszawski, L., Schewe, J., and Piontek, F.: A trend-preserving bias correction – the ISIMIP approach, Earth Syst. Dynam., 4, 219–236, https://doi.org/10.5194/esd-4-219-2013, 2013.
Huisman, J. A., Breuer, L., Bormann, H., Bronstert, A., Croke, B. F. W., Frede, H.-G., Gräff, T., Hubrechts, L., Jakeman, A. J., Kite, G., Lanini, J., Leavesley, G., Lettenmaier, D. P., Lindström, G., Seibert, J., Sivapalan, M., Viney, N. R., and Willems, P.: Assessing the impact of land use change on hydrology by ensemble modeling (LUCHEM) III: scenario analysis, Adv. Water Resour., 32, 159–170, https://doi.org/10.1016/j.advwatres.2008.06.009, 2009.
Huntzinger, D. N., Schwalm, C., Michalak, A. M., Schaefer, K., King, A. W., Wei, Y., Jacobson, A., Liu, S., Cook, R. B., Post, W. M., Berthier, G., Hayes, D., Huang, M., Ito, A., Lei, H., Lu, C., Mao, J., Peng, C. H., Peng, S., Poulter, B., Riccuito, D., Shi, X., Tian, H., Wang, W., Zeng, N., Zhao, F., and Zhu, Q.: The North American Carbon Program Multi-Scale Synthesis and Terrestrial Model Intercomparison Project – Part 1: Overview and experimental design, Geosci. Model Dev., 6, 2121–2133, https://doi.org/10.5194/gmd-6-2121-2013, 2013.
Huntzinger, D. N., Michalak, A. M., Schwalm, C., Ciais, P., King, A. W., Fang, Y., Schaefer, K., Wei, Y., Cook, R. B., Fisher, J. B., Hayes, D., Huang, M., Ito, A., Jain, A. K., Lei, H., Lu, C., Maignan, F., Mao, J., Parazoo, N., Peng, S., Poulter, B., Ricciuto, D., Shi, X., Tian, H., Wang, W., Zeng, N., and Zhao, F.: Uncertainty in the response of terrestrial carbon sink to environmental drivers undermines carbon-climate feedback predictions, Sci. Rep.-UK, 7, 4765, https://doi.org/10.1038/s41598-017-03818-2, 2017.
Ito, A. and Inatomi, M.: Water-use efficiency of the terrestrial biosphere: a model analysis focusing on interactions between the global carbon and water cycles, J. Hydrometeorol., 13, 681–694, https://doi.org/10.1175/JHM-D-10-05034.1, 2012.
Jung, M.: FLUXCOM (RS+METEO) Global Land Carbon Fluxes using CRUNCEP climate data, [dataset], Max Planck Institute for Biogeochemistry, available at: https://doi.org/10.17871/FLUXCOM_RS_METEO_CRUNCEPv6_1980_2013_v1 (last access: 28 July 2017), 2016.
Jung, M., Reichstein, M., and Bondeau, A.: Towards global empirical upscaling of FLUXNET eddy covariance observations: validation of a model tree ensemble approach using a biosphere model, Biogeosciences, 6, 2001–2013, https://doi.org/10.5194/bg-6-2001-2009, 2009.
Jung, M., Reichstein, M., Margolis, H. A., Cescatti, A., Richardson, A. D., Arain, M. A., Arneth, A., Bernhofer, C., Bonal, D., Chen, J., Gianelle, D., Gobron, N., Kiely, G., Kutsch, W., Lasslop, G., Law, B. E., Lindroth, A., Merbold, L., Montagnani, L., Moors, E. J., Papale, D., Sottocornola, M., Vaccari, F., and Williams, C.: Global patterns of land–atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations, J. Geophys. Res.-Biogeo., 116, G00J07, https://doi.org/10.1029/2010JG001566, 2011.
Jung, M., Reichstein, M., Schwalm, C. R., Huntingford, C., Sitch, S., Ahlström, A., Arneth, A., Camps-Valls, G., Ciais, P., Friedlingstein, P., Gans, F., Ichii, K., Jain, A. K., Kato, E., Papale, D., Poulter, B., Raduly, B., Rödenbeck, C., Tramontana, G., Viovy, N., Wang, Y.-P., Weber, U., Zaehle, S., and Zeng, N.: Compensatory water effects link yearly global land CO2 sink changes to temperature, Nature, 541, 516–520, https://doi.org/10.1038/nature20780, 2017.
Knutti, R., Masson, D., and Gettelman, A.: Climate model genealogy: generation CMIP5 and how we got there, Geophys. Res. Lett., 40, 1194–1199, https://doi.org/10.1002/grl.50256, 2013.
Krishnamurti, T. N., Kishtawal, C. M., LaRow, T. E., Bachiochi, D. R., Zhang, Z., Williford, C. E., Gadgil, S., and Surendran, S.: Improved weather and seasonal climate forecasts from multimodel superensemble, Science, 80, 1548–1550, https://doi.org/10.1126/science.285.5433.1548, 1999.
Lasslop, G., Reichstein, M., Papale, D., Richardson, A. D., Arneth, A., Barr, A., Stoy, P., and Wohlfahrt, G.: Separation of net ecosystem exchange into assimilation and respiration using a light response curve approach: critical issues and global evaluation, Glob. Change Biol., 16, 187–208, https://doi.org/10.1111/j.1365-2486.2009.02041.x, 2009.
Le Quéré, C., Raupach, M. R., Canadell, J. G., Marland, G., Bopp, L., Ciais, P., Conway, T. J., Doney, S. C., Feely, R. A., Foster, P., Friedlingstein, P., Gurney, K., Houghton, R. A., House, J. I., Huntingford, C., Levy, P. E., Lomas, M. R., Majkut, J., Metzl, N., Ometto, J. P., Peters, G. P., Prentice, I. C., Randerson, J. T., Running, S. W., Sarmiento, J. L., Schuster, U., Sitch, S., Takahashi, T., Viovy, N., van der Werf, G. R., and Woodward, F. I.: Trends in the sources and sinks of carbon dioxide, Nat. Geosci., 2, 831–836, https://doi.org/10.1038/ngeo689, 2009.
Lovenduski, N. S. and Bonan, G. B.: Reducing uncertainty in projections of terrestrial carbon uptake, Environ. Res. Lett., 12, 44020, https://doi.org/10.1088/1748-9326/aa66b8, 2017.
Moncrieff, G. R., Scheiter, S., Langan, L., Trabucco, A., and Higgins, S. I.: The future distribution of the savannah biome: model-based and biogeographic contingency, Philos. T. R. Soc. B, 371, 20150311, https://doi.org/10.1098/rstb.2015.0311, 2016.
Myneni, R. B., Hoffman, S., Knyazikhin, Y., Privette, J. L., Glassy, J., Tian, Y., Wang, Y., Song, X., Zhang, Y., Smith, G. R., Lotsch, A., Friedl, M., Morisette, J. T., Votava, P., Nemani, R. R., and Running, S. W.: Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data, Remote Sens. Environ., 83, 214–231, 2002.
Nishina, K., Ito, A., Beerling, D. J., Cadule, P., Ciais, P., Clark, D. B., Falloon, P., Friend, A. D., Kahana, R., Kato, E., Keribin, R., Lucht, W., Lomas, M., Rademacher, T. T., Pavlick, R., Schaphoff, S., Vuichard, N., Warszawaski, L., and Yokohata, T.: Quantifying uncertainties in soil carbon responses to changes in global mean temperature and precipitation, Earth Syst. Dynam., 5, 197–209, https://doi.org/10.5194/esd-5-197-2014, 2014.
Nishina, K., Ito, A., Falloon, P., Friend, A. D., Beerling, D. J., Ciais, P., Clark, D. B., Kahana, R., Kato, E., Lucht, W., Lomas, M., Pavlick, R., Schaphoff, S., Warszawaski, L., and Yokohata, T.: Decomposing uncertainties in the future terrestrial carbon budget associated with emission scenarios, climate projections, and ecosystem simulations using the ISIMIP results, Earth Syst. Dynam., 6, 435–445, https://doi.org/10.5194/esd-6-435-2015, 2015.
Norby, R. J., Warren, J. M., Iversen, C. M., Medlyn, B. E., and McMurtrie, R. E.: CO2 enhancement of forest productivity constrained by limited nitrogen availability, P. Natl. Acad. Sci. USA, 107, 19368–19373, https://doi.org/10.1073/pnas.1006463107, 2010.
Pavlick, R., Drewry, D. T., Bohn, K., Reu, B., and Kleidon, A.: The Jena Diversity-Dynamic Global Vegetation Model (JeDi-DGVM): a diverse approach to representing terrestrial biogeography and biogeochemistry based on plant functional trade-offs, Biogeosciences, 10, 4137–4177, https://doi.org/10.5194/bg-10-4137-2013, 2013.
Poulter, B., Frank, D., Ciais, P., Myneni, R. B., Andela, N., Bi, J., Broquet, G., Canadell, J. G., Chevallier, F., Liu, Y. Y., Running, S. W., Sitch, S., and van der Werf, G. R.: Contribution of semi-arid ecosystems to interannual variability of the global carbon cycle, Nature, 509, 600–603, https://doi.org/10.1038/nature13376, 2014.
Raftery, A. E., Gneiting, T., Balabdaoui, F., and Polakowski, M.: Using bayesian model averaging to calibrate forecast ensembles, Mon. Weather Rev., 133, 1155–1174, https://doi.org/10.1175/MWR2906.1, 2005.
Rammig, A., Jupp, T., Thonicke, K., Tietjen, B., Heinke, J., Ostberg, S., Lucht, W., Cramer, W., and Cox, P.: Estimating the risk of Amazonian forest dieback, New Phytol., 187, 694–706, https://doi.org/10.1111/j.1469-8137.2010.03318.x, 2010.
Reichstein, M., Falge, E., Baldocchi, D., Papale, D., Aubinet, M., Berbigier, P., Bernhofer, C., Buchmann, N., Gilmanov, T., Granier, A., Grunwald, T., Havrankova, K., Ilvesniemi, H., Janous, D., Knohl, A., Laurila, T., Lohila, A., Loustau, D., Matteucci, G., Meyers, T., Miglietta, F., Ourcival, J.-M., Pumpanen, J., Rambal, S., Rotenberg, E., Sanz, M., Tenhunen, J., Seufert, G., Vaccari, F., Vesala, T., Yakir, D., and Valentini, R.: On the separation of net ecosystem exchange into assimilation and ecosystem respiration: review and improved algorithm, Glob. Change Biol., 11, 1424–1439, 2005.
Running, S. W., Nemani, R. R., Heinsch, F. A., Zhao, M., Reeves, M., and Hashimoto, H.: A continuous satellite-derived measure of global terrestrial primary production, Bioscience, 54, 547, https://doi.org/10.1641/0006-3568(2004)054[0547:ACSMOG]2.0.CO;2, 2004.
Saatchi, S. S., Harris, N. L., Brown, S., Lefsky, M., Mitchard, E. T. A., Salas, W., Zutta, B. R., Buermann, W., Lewis, S. L., Hagen, S., Petrova, S., White, L., Silman, M., and Morel, A.: Benchmark map of forest carbon stocks in tropical regions across three continents, P. Natl. Acad. Sci. USA, 108, 9899–9904, https://doi.org/10.1073/pnas.1019576108, 2011.
Schwalm, C. R., Huntzinger, D. N., Fisher, J. B., Michalak, A. M., Bowman, K., Ciais, P., Cook, R., El-Masri, B., Hayes, D., Huang, M., Ito, A., Jain, A., King, A. W., Lei, H., Liu, J., Lu, C., Mao, J., Peng, S., Poulter, B., Ricciuto, D., Schaefer, K., Shi, X., Tao, B., Tian, H., Wang, W., Wei, Y., Yang, J., and Zeng, N.: Toward “optimal” integration of terrestrial biosphere models, Geophys. Res. Lett., 42, 4418–4428, https://doi.org/10.1002/2015GL064002, 2015.
Shamseldin, A. Y., O'Connor, K. M., and Liang, G. C.: Methods for combining the outputs of different rainfall–runoff models, J. Hydrol., 197, 203–229, https://doi.org/10.1016/S0022-1694(96)03259-3, 1997.
Sitch, S., Smith, B., Prentice, I. C., Arneth, A., Bondeau, A., Cramer, W., Kaplan, J. O., Levis, S., Lucht, W., Sykes, M. T., Thonicke, K., and Venevsky, S.: Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model, Glob. Change Biol., 9, 161–185, https://doi.org/10.1046/j.1365-2486.2003.00569.x, 2003.
Smallman, T. L., Exbrayat, J.-F., Mencuccini, M., Bloom, A. A., and Williams, M.: Assimilation of repeated woody biomass observations constrains decadal ecosystem carbon cycle uncertainty in aggrading forests, J. Geophys. Res.-Biogeo., 122, 528–545, https://doi.org/10.1002/2016JG003520, 2017.
Smith, W. K., Reed, S. C., Cleveland, C. C., Ballantyne, A. P., Anderegg, W. R. L., Wieder, W. R., Liu, Y. Y., and Running, S. W.: Large divergence of satellite and Earth system model estimates of global terrestrial CO2 fertilization, Nat. Clim. Change, 6, 306–310, https://doi.org/10.1038/nclimate2879, 2015.
Taylor, K. E., Stouffer, R. J., and Meehl, G. A.: An overview of CMIP5 and the experiment design, B. Am. Meteorol. Soc., 93, 485–498, https://doi.org/10.1175/BAMS-D-11-00094.1, 2012.
Thornton, P. E., Doney, S. C., Lindsay, K., Moore, J. K., Mahowald, N., Randerson, J. T., Fung, I., Lamarque, J.-F., Feddema, J. J., and Lee, Y.-H.: Carbon-nitrogen interactions regulate climate-carbon cycle feedbacks: results from an atmosphere-ocean general circulation model, Biogeosciences, 6, 2099–2120, https://doi.org/10.5194/bg-6-2099-2009, 2009.
Tjoelker, M. G., Oleksyn, J., and Reich, P. B.: Modelling respiration of vegetation: Evidence for a general temperature-dependent Q10, Glob. Chang. Biol., 7, 223–230, https://doi.org/10.1046/j.1365-2486.2001.00397.x, 2001.
Tramontana, G., Jung, M., Schwalm, C. R., Ichii, K., Camps-Valls, G., Ráduly, B., Reichstein, M., Arain, M. A., Cescatti, A., Kiely, G., Merbold, L., Serrano-Ortiz, P., Sickert, S., Wolf, S., and Papale, D.: Predicting carbon dioxide and energy fluxes across global FLUXNET sites with regression algorithms, Biogeosciences, 13, 4291–4313, https://doi.org/10.5194/bg-13-4291-2016, 2016.
Viney, N. R., Bormann, H., Breuer, L., Bronstert, A., Croke, B. F. W., Frede, H., Gräff, T., Hubrechts, L., Huisman, J. A., Jakeman, A. J., Kite, G. W., Lanini, J., Leavesley, G., Lettenmaier, D. P., Lindström, G., Seibert, J., Sivapalan, M., and Willems, P.: Assessing the impact of land use change on hydrology by ensemble modelling (LUCHEM) II: ensemble combinations and predictions, Adv. Water Resour., 32, 147–158, https://doi.org/10.1016/j.advwatres.2008.05.006, 2009.
Warszawski, L., Frieler, K., Huber, V., Piontek, F., Serdeczny, O., and Schewe, J.: The Inter-Sectoral Impact Model Intercomparison Project (ISIMIP): project framework, P. Natl. Acad. Sci. USA, 111, 3228–32, https://doi.org/10.1073/pnas.1312330110, 2014.
Watanabe, S., Hajima, T., Sudo, K., Nagashima, T., Takemura, T., Okajima, H., Nozawa, T., Kawase, H., Abe, M., Yokohata, T., Ise, T., Sato, H., Kato, E., Takata, K., Emori, S., and Kawamiya, M.: MIROC-ESM 2010: model description and basic results of CMIP5-20c3m experiments, Geosci. Model Dev., 4, 845–872, https://doi.org/10.5194/gmd-4-845-2011, 2011.
Wieder, W. R., Cleveland, C. C., Smith, W. K., and Todd-Brown, K. E. O.: Future productivity and carbon storage limited by terrestrial nutrient availability, Nat. Geosci., 8, 441–444, https://doi.org/10.1038/ngeo2413, 2015.
Williams, M., Schwarz, P. A., Law, B. E., Irvine, J., and Kurpius, M. R.: An improved analysis of forest carbon dynamics using data assimilation, Glob. Change Biol., 11, 89–105, https://doi.org/10.1111/j.1365-2486.2004.00891.x, 2005.
Woodward, F., Smith, T., and Emanuel, W.: A global land primary productivity and phytogeography model, Global Biogeochem. Cy., 9, 471–490, 1995.
Zhang, Q., Wang, Y. P., Pitman, A. J., and Dai, Y. J.: Limitations of nitrogen and phosphorous on the terrestrial carbon uptake in the 20th century, Geophys. Res. Lett., 38, L22701, https://doi.org/10.1029/2011GL049244, 2011.
Zhang, Q., Wang, Y. P., Matear, R. J., Pitman, A. J., and Dai, Y. J.: Nitrogen and phosphorous limitations significantly reduce future allowable CO2 emissions, Geophys. Res. Lett., 41, 632–637, https://doi.org/10.1002/2013GL058352, 2013.
Zhao, M. and Running, S. W.: Drought-induced reduction in global, Science, 329, 940–943, https://doi.org/10.1126/science.1192666, 2010 (data available at: http://files.ntsg.umt.edu/data/NTSG_Products/MOD17/GeoTIFF/MOD17A3/, last access: 17 August 2017).
Zhao, M., Heinsch, F. A., Nemani, R. R., and Running, S. W.: Improvements of the MODIS terrestrial gross and net primary production global data set, Remote Sens. Environ., 95, 164–176, https://doi.org/10.1016/j.rse.2004.12.011, 2005 (data available at: http://files.ntsg.umt.edu/data/NTSG_Products/MOD17/GeoTIFF/MOD17A3/, last access: 17 August 2017).