The Pareto effect in tipping social networks: from minority to majority

How do social networks tip? A popular theory is that a small minority can trigger population-wide social change. This aligns with the Pareto principle, a semi-quantitative law which suggests that, in many systems, 80 % of effects arise from 20 % of the causes. In the context of the transition to net-zero emissions, this vital 20 % can be a critical instigator of social tipping, a process which can rapidly change social norms. In this work, we asked whether the Pareto effect can be observed in social systems by conducting a literature review, placing a focus on social norm diffusion and complex contagion via social networks. By analysing simulation and empirical results of social tipping events across disciplines and a large parametric space, we identified consistent patterns across studies and key factors which help or hinder social tipping. We show evidence supporting a tipping point near 25 % of the total population within our compiled dataset. Near this critical mass, we observe a high likelihood for a social tipping event, where a large majority quickly adopts new norms. Our findings illustrate slight variations between modelling and empirical results, with average tipping points at 24 % and 27 %, respectively. Additionally, we show a range of critical masses where social tipping is possible; these values lie between 10 % and 43 %. These results indicate the potential, but not the inevitability, of rapid social change in certain susceptible populations and contexts. Finally, we provide practical guidance for facilitating difficult norm changes by (1) leveraging trusted community structures and building critical mass in clustered networks (particularly in the 10 %–43 % threshold range), (2) adapting strategies based on norm type and context, and (3) targeting groups with moderate preferences and network positions – avoiding reliance on highly central or well-connected individuals – to enable endogenous spread.

1 Introduction

Non-linear dynamical systems, under which social tipping processes (social tipping) can be considered, have been studied comprehensively by both natural (Strogatz, 2019) and social scientists over the last century. Famous examples are Granovetter (1973), who showed that a select minority can alter the macro-scale information flow in certain social network structures, and Schelling (1971), who demonstrated that a slight individual racial preference can lead to completely segregated neighbourhoods. Some contemporary authors have focused on rapid shifts in smoking behaviour (Nyborg et al., 2016) and the critical mass phenomenon, whereby the participation of a minority (25 %–30 %) in a collective event can engage the remaining majority (Andreoni et al., 2021; Centola et al., 2018). As recognition of the close coupling between social and physical systems characteristic of the Anthropocene has increased (Lenton, 2020; Steffen et al., 2018), so has research on social tipping processes in the context of climate and global environmental change, since these can act as mechanisms of rapid societal transformation (Constantino et al., 2022; David Tàbara et al., 2018; Lenton, 2020; Nyborg et al., 2016; Otto et al., 2020b; Westley et al., 2011). This new area of tipping scholarship is centred around deliberately bringing about social change through targeted action on tipping elements at sensitive intervention points (Farmer et al., 2019) or at moments of opportunity that trigger a tipping point. It is important to note that the definitions of tipping points in a socio-ecological system (SES) context are not uniform. In Sect. 2.1 of this paper, we provide a concise summary as a guide for understanding these definitions in the context of this work.

New research in this sector can be broken down into analyses and analytical frameworks. Key examples of the former are seen in Otto et al. (2020b), who identified several concrete societal tipping elements and timescales through expert elicitation, while Farmer et al. (2019) and Lenton (2020) also indicated critical points for intervention in financial, energy, resource, and governance systems, to name a few. Frameworks refer more generally to processes, phases, and conceptualisations of “radical” socio-ecological transitions (Feola, 2015). More recent work (Winkelmann et al., 2022) proposed a framework that includes a more detailed description of social tipping mechanisms and explicitly incorporated critical elements such as social network properties (e.g. polarisation, clustering, and modularity), agency, temporospatial scales, and dynamics like social contagion and network adaptation. Much of this work emphasises the existence or identification of social tipping points, the need to trigger them, and their value in the sustainability transition. Many theories specific to modelling social tipping in social–environmental systems as opposed to general social systems have been proposed (Lade et al., 2017; Müller-Hansen et al., 2017; Schwarz et al., 2020; Schwarz and Ernst, 2009), and a body (Andersson et al., 2021; Frei et al., 2023; Geier et al., 2019; Schleussner et al., 2016; Schunck et al., 2024) of recent empirical work in the fields of statistical physics, network science, and computational social science also acknowledges their applications to the SES transformation.

One theme critically discussed in recent literature is the estimation of social tipping points and whether social tipping is possible at large scales in complex social–ecological systems (Bentley et al., 2014). It is largely understood that any general tipping point is difficult to predict due to the system's complexity, heterogeneity, and dependence on context (Bentley et al., 2014; Constantino et al., 2022; Winkelmann et al., 2022). In some circumstances, these points may not even exist (Ferraz de Arruda et al., 2023). Despite this, evidence for tipping seems to exist, or at least for tipping as it is conceptualised in network theory (Guilbeault et al., 2018), across and between societies, scopes, and organisms (Dodds and Watts, 2004). A significant number of overlaps or co-occurrences observed in empirical and modelling results for social contagion processes from various disciplines confirm this (Andreoni et al., 2021; Centola et al., 2018; Wiedermann et al., 2020; Xie et al., 2011). While it is highly unlikely that the employed methods will ever be quantitatively used to estimate tipping points across systems, the results obtained can be used to identify a range of scenarios where tipping is more likely.

Social networks and network science methods are critical tools for understanding social tipping processes (Granovetter, 1978; Watts and Dodds, 2007; Watts and Strogatz, 1998). While many other approaches are viable, networks effectively represent social interactions – a fundamental part of social processes (Berner et al., 2023; Guilbeault et al., 2018; Sayama et al., 2013; Smaldino, 2023). Some of the tipping literature acknowledges this (Constantino et al., 2022; Smith et al., 2025; Winkelmann et al., 2022), but, to our knowledge, no literature solely presents a network-based perspective. The conducted literature review enabled us to determine how previous findings and the social tipping concept can be complemented by network theory. Ideally, this will improve our understanding of this perspective and advance methodological approaches. While we limited our scope to social networks, we also limited the scope of what we recognised as social tipping in this article. Social tipping processes can lead to high-level changes in the socio-techno sphere, for example, by reducing EV battery costs or the legislative sphere by changing how climate change is integrated in school curricula. We did not consider this level of abstraction in this work and focused solely on social tipping in terms of the change in and transfer of norms, values, or behaviours between people. Although this work is slightly removed from the sustainability and climate change context, where social tipping is usually discussed, we and several others (Constantino et al., 2022; Holme and Rocha, 2023; Smith et al., 2025; Winkelmann et al., 2022) believe that the insights provided by studying a network and by taking a complex contagion-centred approach are necessary to better understand higher-level tipping in sectors that are crucial for social transformations.

Firstly, we quantified general trends in the social tipping literature in several disciplines. This task presents significant challenges due to cross-disciplinary dataset complexity, inconsistent terminology, and numerous confounding factors in social tipping (Milkoreit, 2023). This task is made especially difficult when intending to include a quantitative analysis, where variables such as critical mass and tipping thresholds (macroscopic and individual) have different dimensions. To ensure robust results, we focused on identifying the marginal effects of individual factors where many explanatory variables were involved. We also provide a range of social tipping thresholds, instead of a single macroscopic threshold. Hence, in this work, we focused on establishing the upper limit of the societal critical mass required to trigger a social tipping event, even in difficult-to-tip systems. Secondly, we investigated the Pareto effect in susceptible social systems. The Pareto effect is consistent with the principle that 80 % of an effect arises from 20 % of the causes (Pareto, 1971). Although this term broadly describes non-linear phenomena across diverse fields, in our research it specifically denotes how a small minority (roughly 20 %) can trigger system-wide social change, influencing approximately 80 % of the population. As a well-known term across many spheres (Dunford et al., 2014), from land ownership to economic distributions, it can help communicate relatively technical knowledge to a non-scientific audience. Lastly, we wanted to bridge the conceptual and terminological gap between the network science and social tipping literature. By analysing the literature identified in our initial database search, we could systemically identify several critical factors influencing tipping processes in a subset of social systems. With these as our guide, we qualitatively reviewed each factor and synthesised the existing information from the relevant literature, reporting the results in Sect. 2. In the next steps, we limited our analysis to literature which explicitly incorporated networks and included only those that reported empirical results. Finally, we relate our findings to social tipping in a concrete and applicable fashion in Sect. 4.3. Our goal was to verify the Pareto effect in social tipping processes, conduct a broad-scope quantitative review of influencing processes, and define a realm of possibility where tipping is most likely to occur.

2 Literature review of tipping in social networks

2.1 What is social tipping?

The terms and definitions used in the interdisciplinary field of social tipping research are quite inconsistent. Mixed meanings occur: terms are appropriated for different contexts, and, in the process, slight changes occur in their meanings (Milkoreit, 2023). It is easier to begin by describing the characteristics of social tipping where the literature on the topic is more consistent (Hodbod et al., 2024; Milkoreit, 2023; Milkoreit et al., 2018; Winkelmann et al., 2022). Even here, the terms social tipping points and social tipping processes are easily conflated, although the former is strictly a feature of the latter. Four primary characteristics of social tipping processes in the context of social–ecological systems are non-linearity (abruptness), positive feedback as a change mechanism, multiple stable states, and limited reversibility. The definitions provided below were included because they reference or have some or all of these characteristics.

In this paper, we use published definitions as much as possible, but we define or re-define specific terms where necessary for the purposes of our analysis and for improved clarity. Tipping refers to a phenomenon where a relatively small change or intervention in a system leads to a large change (or to large changes) on a macroscopic level (Milkoreit, 2023). The term tipping point originated from social science research on racial segregation patterns (Grodzins, 1957) and was used to refer to thresholds for the racial composition of neighbourhoods in the US in the 1950s. When these thresholds were crossed, people with the minority skin colour felt uncomfortable and tended to move out. More recently, the term was popularised by Gladwell's (2001) book on trends in human behaviour and consumption and in technology change. The definition of tipping elements originated, however, in work on the Earth's climate system (Lenton et al., 2008). Since these terms were established, they have been broadly used in various scientific disciplines in the natural (Holland et al., 2006; Scheffer et al., 2012; Dakos and Bascompte, 2014) and social sciences (Grodzins, 1957; Milkoreit et al., 2018; Schelling, 1971; Winkelmann et al., 2022). Our unit of analysis in this article, i.e. networks of social agents capable of undergoing non-linear changes, is consistent with existing definitions of social tipping elements in this body of work. A formal definition of the term social tipping was proposed by Otto et al. (2020b). These authors stated that social tipping involves a discontinuous state transition in the underlying system; i.e. it is more than a rapid continuous change (triggering phase). The emergence of the new state, however, can be gradual (manifestation phase). A more mathematical definition of social tipping using a criticality framework was recently introduced by Winkelmann et al. (2022). This definition and approach have been expanded by others (Smith et al., 2025). This criticality-centred definition of social tipping differs significantly from the definition of social tipping introduced in this paper. Rather than focusing on criticality, we introduce simple criteria (Box 1) for the shift from a minority to a majority, which we explain further later in the paper. Lastly, the term spillovers, as used, for example, by Berger et al. (2021) and Efferson et al. (2020), is a useful framework for social tipping, particularly in the context of exogenous changes to a social system, i.e. interventions. A spillover is an indirect systemic effect produced by an endogenous response to an intervention on a single individual or on a few individuals. This is larger than the effect of the intervention itself.

In this article, we present a quantitative analysis of minority-induced social tipping, focusing on cases where early adopters of a new norm comprise less than 50 % of the population. For our quantitative results (Figs. 4, 5), we operationalise social tipping as instances that meet the criteria for a social tipping event as defined in Box 1, specifically where the fraction of adopters of a norm transitions from a minority (f₀<0.5) to a majority (f_∞ > 0.5). However, we relax this constraint in Sect. 2 to discuss a wider evidence base and refer to the broader definition by Milkoreit (2023), as described above. Figure 1a shows the stricter definition as a shaded blue social tipping zone, a scenario in which a minority group of actors has convinced a majority group to adopt another social norm. This is also what is referred to as a contagion event or a cascade in network theoretic terms (Box 1). Figure 1a also depicts a characteristic feature of social tipping, i.e. its non-linearity, a non-linear increase in a system state variable for a given increase in a system control parameter, or a state variable itself (Strogatz, 2019). This non-linearity in social systems implies that a marginal effect of norm adoption, e.g. one individual adopting a new norm, can have a large effect on the final fraction of people adopting this new norm after a social tipping event. Figure 1a demonstrates this under the assumption that the exemplary social system can undergo a social tipping process. In this example, alternative norm adoption by ∼ 20 % of the population leads to a steady-state alternative norm adoption of around ∼ 80 %, demonstrating the theoretical Pareto or minority tipping effect.

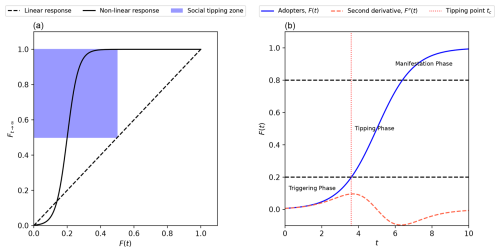
Figure 1 (a) The line denoted “non-linear response” characterises the predicted steady-state behaviour of a social system in response to an increasing fraction of individuals adopting an alternative norm, F(t). Social tipping as defined for the purposes of our quantitative analysis is depicted as the blue-shaded region. (b) In blue, the evolution of the alternative norm adopter fraction over time is predicted in a social system undergoing a social tipping event. The tipping threshold is defined as the adopter fraction at the maximum of its second derivative, the tipping point t_c, shown here as a vertical dotted red line. We use these two definitions as a conceptual base for our review and its methodology.

The tipping point can be identified as the point in time where the fraction of norm adopters F(t) has the most potential to induce a social tipping event. How do we define this point? We conceptualise this simply for the purposes of our analysis by using the second derivative of the state variable, F(t). The maximum value of this second derivative is the point where the acceleration in the rate of norm adoption is the greatest. We assume this is the point most likely to lead to a social tipping event, if it is possible within the given social system. Jin and Yu (2021) also adopted this measure to classify the tipping threshold of a networked social system under complex contagion conditions, classified as the chance of tipping based on a perturbation or marginal (individual) norm change. In Fig. 1b, we plot this fraction F(t). We apply the language from Otto et al. (2020b) here to illustrate these stages.

Box 1 Key terms which are helpful for understanding the concepts presented in this article. Definitions may be similar to those in other works but have been slightly changed to apply to our analysis.

2.2 Networks and tipping

Social processes are governed by relationships among people. The spatial and temporal sum of these connections constitutes social networks. In this sense, the network structure is fundamental to flows that occur via a social network and critically affects tipping processes (Dodds and Watts, 2004). A formal description of networks is usually the mathematical concept of a graph. In their simplest form, networks consist of nodes and links (Berner et al., 2023). Thus, a network N can be fully described by the tuple $N=(V,E)$, where V is the set of all nodes and E is the set of all links. Here, nodes can be people, animals, or molecules, and the links can be Facebook interactions, mating relationships, or bonds. Before giving specific examples of networks, it is important to distinguish adaptive, temporal, and static networks. Intuitively, the first two change their structures over time, while the latter does not (Holme, 2015).

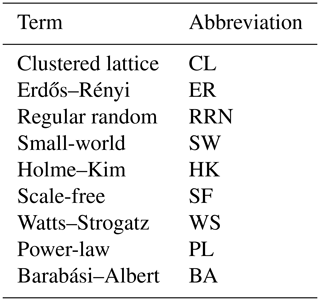
Adaptive networks and temporal networks both shape and are shaped by dynamic processes that occur in them, but the topology of the former takes precedence over the temporality or timing of events (Berner et al., 2023; Holme, 2015). Considering that all social networks are predicated on social interaction and constantly change, for all intents and purposes, static networks are either representations of aggregated social interactions or network processes, such as rewiring, over a period (time-aggregated networks). They can also represent a static slice of a network, i.e. at a fixed time point. A concrete example of a social network would be attendees of a conference and their interactions. In this case, each user is a node, and conversations between attendees are represented as links (contacts) between them, forming a human proximity network (Donges et al., 2021; Holme, 2015). The sum of all conversations taking place in the conference period or a snapshot of those currently conversing (e.g. at 15:00 LT on a Friday afternoon) would then be a static representation. A temporal or adaptive representation is more difficult to visualise but could be created by plotting the average degree (number of node links) of the graph against time (Holme, 2015). In this work, we consider all three types of networks (i.e. adaptive, temporal, and static), but the majority are either static or adaptive networks. Most of the literature, and especially those examples involving modelling, uses archetypal network topologies representing commonly occurring real-world networks and their properties. One example is small-world networks: these display properties such as high local clustering of nodes and short path lengths, which are often featured by real-world biological, ecological, and social systems (Telesford et al., 2011; Watts and Strogatz, 1998). A visual representation of the most common network topologies in our review appears in Fig. 2.

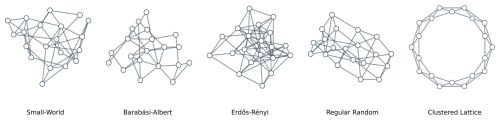
Figure 2 A visual representation of the most common network topologies identified in our literature review; a description of key properties can be found in Table 1.

Table 1 A description of network characteristics for the network topologies shown in Fig. 2.

For the purposes of this work, which was carried out to view social tipping through the lens of network theory, we can generalise social tipping as a contagious spreading process or cascade via a complex network (Guilbeault et al., 2018; Watts, 2002). A definition is given in Box 1. This spreading process can involve behaviours, opinions, knowledge, or social norms (Christakis and Fowler, 2007; Nyborg et al., 2016; Schleussner et al., 2016). The mechanism leading to contagious spreading processes via networks is classified in two main ways: simple contagion and complex contagion (Guilbeault et al., 2018). In the former, an agent can be “infected” by one exposure to another contagious agent, whereby an agent usually requires multiple exposures from different sources in the latter (Centola and Macy, 2007). A notable requirement for the propagation of complex contagion is the presence of wide bridges (Guilbeault and Centola, 2021; Reisinger et al., 2024). A bridge forms a link between two otherwise disconnected subcomponents of a network. This can be a single link between two nodes, a and b. One dimension of this bridge is its length, which is the shortest path between these two nodes. Another is its width, which is the number of ties connecting the neighborhoods of a and b. The latter is critical because it facilitates the requisite multiple exposures of nodes as the contagion travels from node a to node b and thus of node b itself. A wide bridge thus forms a network structure that facilitates the spread of complex contagions through multiple reinforced connections between two neighbourhoods in the network.

In the rest of this article, we will use the term social tipping to refer to a network cascade, implying that these terms have the same meaning when discussing social opinion and norm dynamics in networks. Exceptions to this usage occur when we cite specific literature, where we prefer to distinguish between these terms as originally defined. An important distinction regarding thresholds should be made between the system-level macroscopic tipping threshold and individual agent thresholds. While the former is defined as shown in Fig. 1b and as described in Box 1 as the tipping threshold along a trajectory, the latter refers to the conditions in an agent's immediate social network required for one agent to change their opinion (Watts, 2002). In the most realistic cases, the mean individual threshold will neither equal nor reliably predict a given macroscopic threshold (Wiedermann et al., 2020).

2.3 The role of network structure and attributes

In this section, we examine the effects of network traits or properties on social tipping processes in some well-known network topologies. Not all networks are the same, and the topology can vary based on the social domain (Efferson et al., 2020), social group (Christakis and Fowler, 2008), or social process (Bellotti et al., 2023) represented by the network. For example, financial networks display more inequality in degree distribution than a reference small-world network (Leo et al., 2016), homophilous networks spread health innovation behaviour more effectively than unstructured networks (Centola, 2011), and bursty network interactions can allow contagion events in networks which are otherwise difficult to tip (Karimi and Holme, 2013). Network topology can vary over time or be shaped by social processes, such as those occurring in temporal and adaptive dynamical networks (Berner et al., 2023). This topological change can then affect the social processes, which leads to feedback loops. As such, topology and dynamics in networks are often confounded when trying to explain why they change and evolve (Shalizi and Thomas, 2011). It can be difficult to address the role of network structure when most of the networks discussed in this work are essentially adaptive dynamical networks; i.e. they have constantly evolving structures. Due to this consideration, we address how a given static topology affects cascade dynamics near a certain time point.

By focusing on well-known network topologies, problems related to terms used in different fields can be avoided, for example, where certain network types are ubiquitous, for example, Erdős–Rényi, Barabási–Albert (Albert and Barabási, 2002), or Watts–Strogatz (Watts and Strogatz, 1998) networks (Telesford et al., 2011). A broad base of evidence exists for the existence of common relationships between topology, cascade size, and frequency. For example, evidence from game-theory-based (Ohtsuki et al., 2006), ecology-based (Martin et al., 2020), and social-contagion-based models (Centola, 2011, 2013) shows that a structured network positively affects the magnitude and rate of contagion spread compared to unstructured networks. This finding contrasts with the “strength of weak ties” concept described by Granovetter (1973) and others (Watts and Strogatz, 1998). One way to interpret these contradicting results is to consider that they depend on network size. Centola (2013) demonstrated how weak ties are mildly helpful in contagion spread in small systems, but strong ties and clustered networks are required to produce successful critical mass phenomena in larger systems. Where social tipping to promote sustainability plays out on a global scale, a prerequisite for any mobilisation effort, therefore, is the existence of homophilic, interconnected, and trusting networks. Although this is generally the case (Guilbeault et al., 2018), Efferson et al. (2020) showed how homophily can be detrimental to spillovers in the context of policy interventions when they are too large. This implies that attempts to facilitate norm change exogenously may interact with homophily in detrimental ways once the intervention becomes too strong. Clustering, more specifically, increases the likelihood of repeated exposures to a contagion source and locks the information within a community (Fink et al., 2016). This second aspect is fundamental for reaching a critical mass (Centola, 2010) and halting the dispersion of a social contagion for long enough that a percolating cluster can form (Box 1). Overall, complex contagion requires a network to have communities which are sufficiently built up but are also connected through wide bridges. This allows ideas to reinforce themselves from within but also offers enough connectivity so these similar clusters can connect at some point (Chiang, 2007). Connectivity is a fundamental part of our world as we know it, characterised by increasingly highly connected global networks; the information supply is higher than ever, and so is the noise (Bak-Coleman et al., 2021). Contagion or information about it tends to die out after more than three network steps (Airoldi and Christakis, 2024; Christakis and Fowler, 2007, 2008; Fowler and Christakis, 2008), indicating that some fundamental laws govern network structures which are conducive to complex contagion.

2.4 The role of an actor's preference and heterogeneity

Successful social tipping processes fundamentally require consecutive individuals or agents to be susceptible to change. Many terms are used to conceptualise this susceptibility. In models of norm change or opinion spread across disciplines, such susceptibility is often operationalised implicitly or explicitly as a threshold (Centola, 2013; Efferson et al., 2020; Granovetter, 1978; Guilbeault et al., 2018; Watts, 2002). A threshold quantifies the point at which an agent will change their behaviour; thus, it governs the magnitude and rate of social tipping in a population. In the real world, this susceptibility varies individually (Efferson et al., 2020) and depends heavily on the type of normative change (Berger et al., 2021; Guilbeault et al., 2018). In other words, both individual thresholds and their governing distributions are heterogeneous. Macroscopic or social-group-level threshold distributions are also emergent, meaning that their shape is not visible or predetermined but arises due to the unique set of interactions occurring among microscopic actors (Wiedermann et al., 2020). This property makes prediction exceedingly difficult, especially with regard to highly polarised or controversial issues. Wiedermann et al. (2020) successfully demonstrated how agents seeded with very narrowly distributed individual thresholds can produce a different system-level distribution. Some models and experiments show the significant effects different threshold distributions have on both cascade speed and magnitude (Andreoni et al., 2021; Berger et al., 2021; Dodds and Watts, 2004; Karsai et al., 2016). Efferson et al. (2020) demonstrated how this effect is also robust to changes in network topology, intervention types, and several other factors. Individuals with high thresholds or even untippable or “immune nodes” regarding a given spreading event can severely hinder or prevent a cascade process (Karsai et al., 2016; Wiedermann et al., 2020). This potential effect is magnified when these nodes occupy key positions in a network, for example, as the first contacts for an innovator or a seed node for a potential network contagion (Reisinger et al., 2024). Optimally, this first contact network should consist of individuals who have typically lower thresholds than normal to enable cascades (Nishioka and Hasegawa, 2022). Efferson et al. (2020) also specifically showed that, under some conditions (where a positive response to an intervention is guaranteed), targeting resilient nodes with policy interventions is more effective than relying on endogenous processes such as tipping or spillovers to evoke norm change.

Thresholds are influenced by several factors, including payoffs, switching incentives (Centola et al., 2018), tension (Berger et al., 2021), and jointness of supply (Centola, 2013). These terms refer to the cost of norm adoption or abandonment. This payoff depends on the network density, social context, and type of norm change (Berger et al., 2021; Constantino et al., 2022; Efferson et al., 2020). Perhaps confusingly, these terms are also used in some models to refer to implicit thresholds, for example, in Andreoni et al. (2021), where tipping thresholds are set by changing miscoordination penalties or by increasing the personal benefit of change. Conversely, explicit thresholds are used to operationalise these same concepts. Examples are seen in Berger et al. (2021) and Efferson et al. (2020), where different threshold distributions are used to represent different social preferences and tension related to a specific dilemma. Based on this example, Fig. 3 displays several theoretical distributions which may represent preferences via tipping thresholds for certain socio-ecological dilemmas and an empirical distribution reconstructed from survey data.

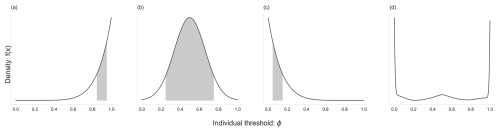
Figure 3 Illustrative individual threshold (ϕ) distributions for a population. These indicate the susceptibility towards changing a specific behaviour or norm in reference to some current social dilemmas surrounding pro-environmental behaviour. Here, panel (a) could represent a decision to become vegan, panel (b) to ride a bike to work, and panel (c) to recycle rubbish and waste. The shaded area represents different strategies for choosing members of a network, i.e. the seeds, to try and promote social tipping. (d) An illustration of the approximate threshold distribution for support of affirmative action in the US, adapted from Janas et al. (2024). The original PMF was derived from an incentivised elicitation method where participants (n=4086) indicated the minimum share of others required to support affirmative action before they would do so themselves. The sample was stratified across racial, ethnic, and gender groups.

Reducing all meat and animal product consumption would correlate with a left-skewed distribution (panel a), meaning that the mean threshold is high and tipping is difficult (Peattie, 2010). In this situation, which depicts a change with high personal cost, most people would only change their dietary habits when a vast majority, i.e. around 70 %, consumes food differently. Intuitively, such a dynamic makes the existence of any minority tipping dynamic unlikely, as a majority (>0.50) has likely already adopted the alternate norm. Some divisive or controversial issues which involve strong ties to personal values or high social pressure may be best characterised by a bimodal distribution. In these cases, the mass of the distribution is concentrated at distinct thresholds, particularly at the extremes of the distribution, representing unconditional positions regardless of others' choices. We see this in panel (d), which depicts an empirical example of thresholds for support (and opposition) for affirmative action, a clearly polarising issue. In this case, intervention strategies targeting individuals with moderate thresholds to build critical mass may be more effective than targeting those most eager to change (Efferson et al., 2020). Regardless of the nomenclature used, several sources show that the successful adoption of a cascading norm or behaviour is highly contingent on the perceived individual benefits, regardless of the magnitude of the cascade (Berger et al., 2021; Centola et al., 2018; Centola, 2013).

2.5 The role of agency and inequalities

In this section, we ask how individuals and groups can intentionally influence the adoption of new patterns of behaviour (Kaaronen and Strelkovskii, 2020) and induce abrupt changes in social conventions and public opinion (Centola et al., 2018; Galam and Cheon, 2020), specifically, how the agency of individuals and groups transforms the social structure, understood as the collective prescriptions and constraints on human behaviour (Granovetter, 1985; Robb, 2014). The social structure is composed of a rule system that constitutes the “grammar” for social action (Otto et al., 2020a). Burns and Flam (1987, p. 26) pointed out that the complex normative network is not given but is a product of human action, stating, “human agents continually form and reform social rule systems”. Human agency is understood as the ability to shape one's life across multiple dimensions: individual agency is reflected in individual choices and life conditions. This individual agency varies strongly within a society based on the individual's age, gender, income, and network position. Collective agency emerges when individuals pool resources to shape their future, while strategic agency refers to the capacity to affect wider system change (Otto et al., 2020a).

In a network-theoretic sense, agency is the ability of a node to control or initiate processes in a network. Where structural properties of a network or a node, such as centrality or degree, strongly influence this ability (Korkmaz et al., 2018), we can use these structural measures as a proxy for a node's agency. Structural properties, while important, are only one aspect. A node's agency also depends on the specific dynamics in each network and the context. Guilbeault and Centola (2021) clearly demonstrate that standard centrality measures, while suitable for predicting the social influence of seed nodes under conditions of simple contagion dynamics, fail under complex contagion conditions. Social influencers, who, in colloquial terms, have high degrees of agency as per our definition above, have been the subject of much contentious debate in several areas dealing with research on social change (Constantino et al., 2022; Han et al., 2020; Hodas and Lerman, 2014; Nielsen et al., 2021; Nishioka and Hasegawa, 2022; Nyborg et al., 2016; Paluck et al., 2016; Paluck and Shepherd, 2012; Watts and Dodds, 2007). Taking an intuitive view of social influencers and their presence in the era of social media platforms, such as TikTok and Instagram, could lead one to believe that they might dramatically shape social opinion and information. However, in the world of complex contagion, which depends on nodes' proximity to wide bridges rather than node degree, they may be surprisingly ineffective (Guilbeault and Centola, 2021; Watts and Dodds, 2007). In fact, “normal” people may be the most cost-effective instigators of change, especially as the volume of information reaching us increases more and more (Bakshy et al., 2011; Fink et al., 2016; Hodas and Lerman, 2014). How does change take place in situations where individuals and groups have different and conflicting interests? Centola (2021) pointed out the role of so-called change agents, who bring innovative solutions into their communities, advocate change, build networks of early adopters, and play pivotal roles in coordinating the new equilibrium and restructuring institutions.

2.6 The role of processes, time, theme, and scale

Temporal processes have a large effect on social tipping dynamics. Due to the interdependence of processes, network structure, and agent state variables, these can be difficult to analyse, as mentioned in Sect. 2.3. Some sources claim that temporal processes can be more important than network topology or can simplify some aspects of complex spreading (Hodas and Lerman, 2014; Karimi and Holme, 2013; Kivelä et al., 2012). In the first study, the duration over which interactions occur strongly affects cascade magnitude and success. To highlight the difficulty of making general statements about these systems, the duration length shows the opposite effect, depending on whether a fractional or absolute threshold is used in the cascade model. The information transmission rate or burstiness can be conducive to complex contagion (Karimi and Holme, 2013), but it has been shown to slow down simple contagion (Karsai et al., 2011). Information about the social norm landscape, both globally (norm average) and locally (close contacts), strongly influences the decision to abandon an old norm or to adopt a new norm (Bergquist and Dinerstein, 2020; Leviston and Uren, 2020; Pieters et al., 1998). This information may pertain to the prevalence of a social norm in society and is very important when the perceived risk or change is high (low payoff). This may happen, for example, when a person decides to abandon a behavioural norm but faces the penalty of alienation from their close social group. When this agent knows that there is global support for an alternative norm despite the group norm, they may be more encouraged to switch regardless. Andreoni et al. (2021) provided evidence for this in a behavioural experiment, where the participants were provided with information about other players' preferences, which were not directly linked to increased contagion size. Jin and Yu (2021) also showed a similar effect by taking a modelling approach. This is a key factor when considering something like pro-environmental behavioural norm changes, like eating less meat (Leviston and Uren, 2020), where the risk of alienation is high. Information frequency or regularity and clarity are then crucial for ensuring social tipping events are noticed by people in a social network, essentially increasing the fraction of people available to engage in norm change. Irregular or delayed belief update times and unclear information dampen social tipping effects and prevent the formation of a critical mass, as people become risk-averse when provided with poor information (Berger et al., 2021; Peattie, 2010). As a caveat, when the information density (i.e. the frequency of providing information over time) becomes too low, social contagions may fail to infect a person, as the person does not attach enough importance to the information or does not notice the signal (Hodas and Lerman, 2014). This can also be thought of as a poor signal-to-noise ratio. Fink et al. (2016) identified this as one factor making nodes with a high in-degree (common with social influencers) and more difficult social contagion targets than others. They are overwhelmed with noise. To a lesser extent, the noise created by our highly interconnected digital global network may make complex contagion generally difficult through these mediums (Bak-Coleman et al., 2021; Hodas and Lerman, 2014).

We established earlier that norms and opinions spread differently from e.g. viruses and memes and that these can be roughly separated into complex and simple contagions, respectively. This simple dichotomy hints at a fundamental principle: that every type of contagion may spread differently. Indeed, as an example, in their long-term study of a network of 12 067 people over 32 years, Christakis and Fowler (2007, 2008) and Fowler and Christakis (2008) showed that the spread of happiness depends more on a person's geographical proximity to a potential contagion source than the spread of healthy eating behaviour. Smoking behaviour transfers very easily to one's spouse, but obesity and happiness do not. Finally, educated people in the USA will have more influence over the smoking behaviour of others, but, in another study on rural communities in India, local elders and knowledge holders only had a marginal effect on the spread of malaria-prevention behaviour (Bellotti et al., 2023). Norms related to controversial topics, such as politics or social movements in response to socio-political issues, show large marginal effects after continued exposure to a norm holder, showing that repeated exposure is critical for opinion change (Fink et al., 2016; Romero et al., 2011). This unique variation in spreading behaviour based on content can make it even more difficult to make estimates. All of these studies still report repeated exposure and social proximity as leading predictors of norm spread between people, supporting arguments for the use of complex social contagion models, even in unfamiliar contexts or under conditions of uncertainty.

3 Data and methods

3.1 Data collection

To identify literature on social tipping in networks from various disciplines, several broad search terms and strings were initially used, as the disciplines employ different nomenclature. Where we explicitly focused on networks, we included this in every search string. A literature search was conducted in the Web of Science and in Google Scholar for the period of 1 January 2001–20 September 2023. Search terms used were “complex contagion” and “social networks”, “norm diffusion” or “complex contagion”, and “social networks”. We identified 33 studies using modelling, observational, or experimental methods to study complex contagion in human networks and that mentioned or referred to empirical results in their abstracts. Another 27 were discovered by examining the reference lists of the initially identified literature and by using comprehensive review articles recently conducted on complex contagions (Guilbeault et al., 2018; Holme and Rocha, 2023). Of the 60 studies identified, 21 were discarded because these still only investigated simple contagion rather than complex contagion models or complex-contagion-like phenomena. We then analysed the final list of the literature in stages. In stage 1, key empirical results were elucidated and coded into a database. In stage 2, we evaluated these key results and the relevant theory (synthesised in Sect. 2). We also looked for finding overlaps and examples of agreement between fields. In this section, we also draw on literature cited in the references of the primary literature to bridge knowledge gaps and to supplement our synthesis. This material was not included in the dataset but can be found in the references. The number of pieces of literature considered in these stages was N=42. In stage 3, we filtered the literature so that only those articles with quantitative results allowing analyses of tipping thresholds were kept. At the end of stage 3, we were left with n=12 articles. A summary of the literature used in stage 1 is displayed in Table 4, and the results are shown in Fig. 4. Stage 3 results are displayed in Fig. 5.

Stage 1 involves classifying key results in terms of how they influence social tipping in networks. Concretely, we applied two criteria: the effect on the rate and magnitude of the social tipping event. Here, the rate refers to the change in the fraction of adopters of an alternative norm per unit time after a tipping point and the magnitude refers to the final fraction of norm adopters. We compared these to a baseline scenario, which was defined as the trajectory with the lowest rate and magnitude in a modelling ensemble or from experimental results. A simple grading system was used to simplify the data collection process, shown in Table 2. Where many of these effects displayed non-monotonic behaviour, we coded them accordingly: these are represented on the x axis in Fig. 5 as “±”. Results which could not be quantitatively graded were marked as having a positive or negative impact on social tipping. A positive (or negative) impact was interpreted as an increase (or decrease) in the probability, speed, or magnitude of a social tipping event. Where similar terms showed conceptual or mechanistic agreement and were used in the same context (i.e. the study evaluated a particular aspect of their effect), we grouped these under an umbrella term. Examples are terms used to describe rewiring (process), an awareness of other people's preferences (process), and weak network ties (structure). All of these can increase the distribution of information through the network to agents and are classified under the umbrella term global information. This is shown in Fig. 4a. A glossary of the terms and their meanings can be found in Appendix A, Table A1. Figure 4b shows the magnitude due to incomplete data for the rate, but this was included for the classification in Fig. 4a. A link to the full dataset, software code for the analysis in Sect. 3.2, and plot reproduction can be found in the “Data availability” section.

Table 2 Categories of grouping terms based on a percent change in the magnitude of a social tipping event compared to a baseline scenario.

3.2 Intercomparison of tipping data from models and experiments

To quantitatively compare tipping data across compatible literature sources, we obtained nine modelling datasets and five experimental datasets either by contacting the respective authors, retrieving published data, or re-running simulations based on software cited in the articles. For literature where none of these things were possible, trajectories or data were extracted directly from articles using optical character recognition (OCR) or other graphical techniques. The models evaluated included complex-contagion-like dynamics, regardless of the technical implementation. This meant that, even if the models did not explicitly use a contagion model, the social spreading dynamics included a threshold-like mechanism of contagion, where agents needed multiple different exposures to be infected. As mentioned in Sect. 2.1, we conducted this review primarily to identify the macroscopic tipping threshold, as this allowed us to bound our analysis and compare units more easily across studies, as most of the literature reporting qualitative results includes time series. This was helpful because the parameter dimensionality can be very high and its overlap can be low. Assuming a time evolution for the fraction of adopters of an alternative norm F(t) in each dataset is present, we calculated the tipping threshold λ from each. We found λ as defined in Sect. 2.1, i.e. the fraction of adopters F(t) at the point where the second derivative reaches its maximum: F(t_c). This can be expressed as

$$\begin{array}{}\text{(1)}& \mathit{\lambda }=F\left(t_c\right)=\underset{t}{max}\left(F^{\prime \prime }\right(t\left)\right),\end{array}$$

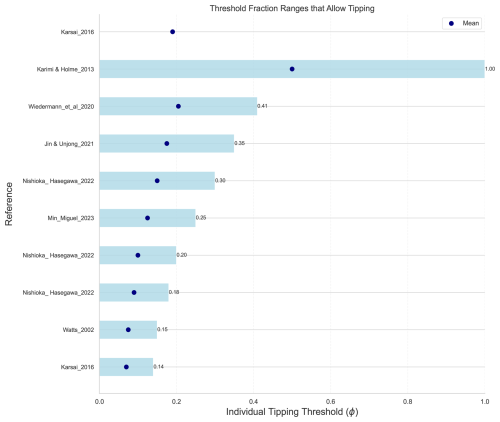
where trajectories were analyzed using finite-difference methods to estimate λ. Where we were also interested in identifying microscopic- or individual-level thresholds, we collected ranges of mean individual thresholds where a cascade event is possible (Appendix B).

4 Results

Below, we summarise the main mechanisms which affect social tipping success as identified by parsing the qualitative results from the literature. A table of terms is provided with network abbreviations.

Table 3 A summary of network topology abbreviations for Table 4.

Table 4 A summary of network topology, the key and supplementary mechanisms which were identified as having an impact on social tipping events. Refer to Table 3 for definitions of network topology abbreviations.

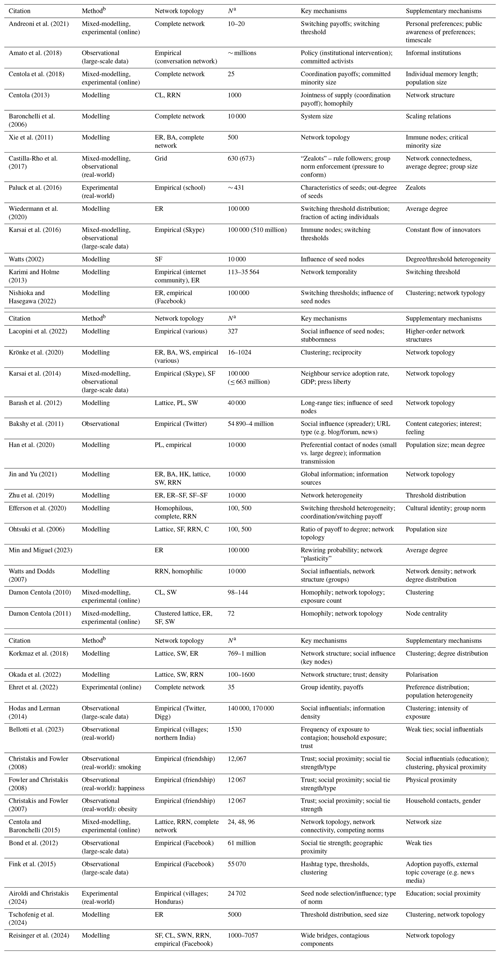
^a Figures in parentheses refer to the population size of observational data (where available) as opposed to the population size of agents or nodes in a model. ^b Modelling here strictly refers to agent-based or simulation modelling as opposed to statistical models or analyses of observational data.

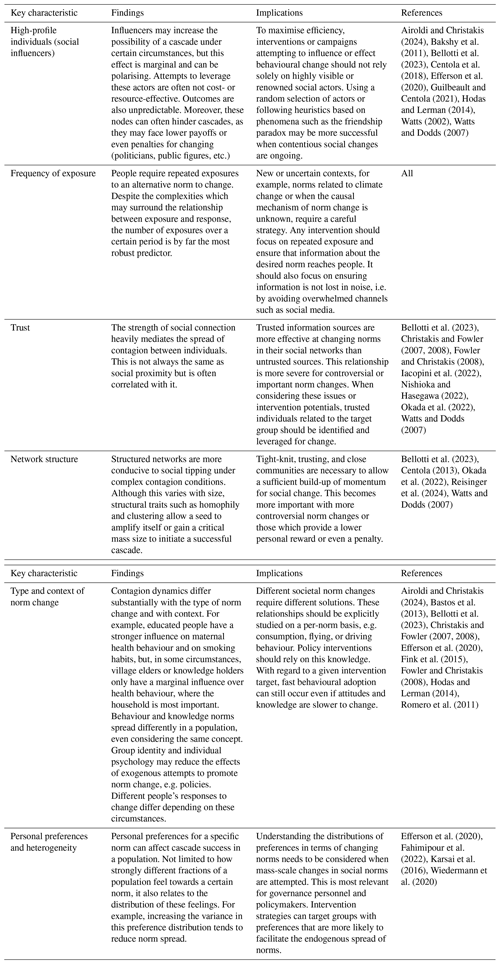
Contradictions regarding several factors were commonly observed in the literature, which was expected given the nature of complex contagion on complex adaptive systems. To estimate the degree of heterogeneity, we counted N = 36 different network topologies and N = 22 different population sizes across the scope of the reviewed articles. Several variables showed non-monotonicity within models and experiments, which are designated by the “±” symbol in Fig. 4a. Some of the most divergent findings are related to homophily, temporal dynamics of network processes, and network size. These are reflected in Fig. 4, where several studies show either positive or negative impacts on social tipping. Despite differences of opinion expressed in the sources, overall, slightly more positive support for homophily appeared in the literature, along with a strong positive effect on tipping cascade size under certain circumstances. Social influence, which was mentioned along with social influencers quite frequently in the articles, is shown to have a positive effect on contagion success and magnitude, as shown in Fig. 4a and b. It is important to note, however, that the term social influence is not the same as social influencer. Factors pertaining to social influencers are multiple and include a high in-degree, which is associated with a reduction in infection probability from a cascade for the reasons mentioned in Sect. 2.6. Broad agreement across the literature was seen that trust and clustering have strong positive effects on cascade magnitude and on overall success. Taken together, clustering, social proximity, and trust were identified as consensus factors in the literature review, based on the signs of their effects. These factors all increase the frequency or number of exposures to close contagion contacts and thus help satisfy the fundamental requirements of complex contagion spread. Conflicting results should not be seen as arguments or weights for the absolute effect of a factor but rather as a tendency or the probability of an effect to influence contagion. This pluralistic approach is necessary, as most of the differences shown in Fig. 4 are due to strong contextual factors influencing the dynamics of the system in question.

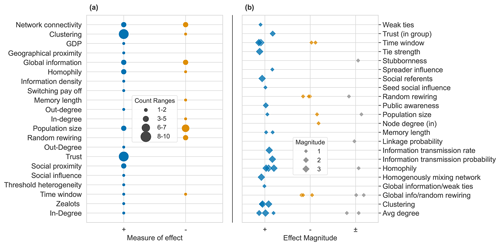
Figure 4 (a) Frequently cited factors influencing complex contagion events in social networks. Summary based on n=95 observations in N=39 studies. Some concepts have been harmonised in an interdisciplinary way where compatible. Factors with a sample size of 1 are not shown here to aid visibility but can be found in the full dataset (Everall, 2025). Population size, global information, and temporal structure show high disagreement across the literature and depend on the context of spreading processes. Trust is a key factor. (b) Factors influencing the magnitude of contagion events in social networks. Values for the literature with more discernible data on effects, n=50. Magnitudes are defined as per Table 2 and range from 0 %–100 % impact on cascade magnitude. The relationship is displayed as an increasing value of the listed factor, set against a baseline scenario (see Sect. 3.1).

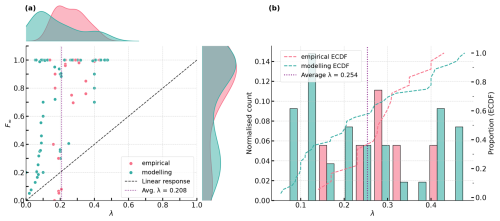
Figure 5 (a) The tipping threshold λ and the steady-state adopter fraction F_∞. Here, we show n=86 modelling and empirical results from N=13 papers on complex contagion in social networks. The bimodal distribution of steady states as shown by the y axis marginal distribution supports theoretical estimates for the non-linearity of social tipping processes. After a critical mass of ∼ 25 % in susceptible populations has been reached, the fraction of norm adopters converges quickly to a fully tipped state (F_∞≈1). (b) The distribution of tipping thresholds. Here, we classify only social tipping events, i.e. F_∞>50 % of the population, numbering n=59. The empirical cumulative distribution function (ECDF) demonstrates that 95 % of critical masses conducive to tipping are <0.4 of the fraction of the population.

Our analysis of critical mass sizes and the steady-state adopter fraction as per Fig. 5 shows that a critical mass of individuals who have adopted a norm exists in susceptible social systems; above this critical mass, the fraction of adopters rapidly increases. This is observed at approximately 25 % of the total population size (modelling: 24 %; empirical: 28 %) when considering only social tipping events and at 21 % when considering all results. This conforms to theoretical estimates of social tipping processes, and it may seem unsurprising that modelling results also replicate this. However, empirical results (i.e. categorising observational and experimental results) are in general agreement with the modelling results and with each other. Empirical results tend to demonstrate sharper thresholds and non-linearity, verging on discontinuity. We also see this effect continuing across timescales. For example, the results shown in Fig. 5 from Amato et al. (2018) have a timescale ranging over centuries, while the behavioural experiments from Centola et al. (2018) and Andreoni et al. (2021) have timescales of days to weeks. This implies a scale invariance in the tipping dynamics with respect to time. Several trajectories do not display social tipping, and some, e.g the cluster of red points at the bottom left of Fig. 5a, do not even demonstrate a positive non-linear response (F_∞>λ), even though the tipping point occurs at a fraction of ∼0.25 or lower. This indicates some systems are not able to see global tipping even if a rapid change in norm adoption occurs in a small fraction of the population. The slightly bimodal distribution in the critical mass size of modelling results (teal) seen along the top margin of Fig. 5 is likely a result of using different modelling approaches to model complex contagion. Some models inherently feature non-linear but continuous transitions to the tipped state, such as the analytical approximation methods of Granovetter's tipping threshold model (Xie et al., 2011), whereas numerical methods tend to show discontinuities. Certain functional forms representing tipping are also responsible, for example, system dynamics models using normal forms to model social tipping (Krönke et al., 2020). These normal forms may inherently feature certain dynamics, such as discontinuous bifurcations. Several models seem to show a bias toward very low critical mass sizes, which is not replicated in the empirical studies. This may suggest that the dynamics or assumptions of these models are not realistic. They provide overly optimistic estimates of the potential for a critical mass to tip a system. It should be noted that, in a large majority of models, the initial seed node or first adopter of an alternative norm was normally taken to be one person or a very small fraction, i.e. <5 % of the total population. Figure 5b demonstrates the range in which social tipping is most likely to occur: 0 %–44 % of the population ECDF⁻¹ (0.95), where the value for empirical data is 40 % and the value for modelling data is 46 %. This implies that values above this threshold involve dynamics that are too linear to be considered social tipping or that there is no critical mass at which the system tips for a given system state (i.e. even at critical masses above this range, no social tipping dynamic is possible). More importantly, 36 % of empirical and 56 % of modelling tipping events occur before or at the critical mass of 25 % of individuals. Although not included in Fig. 5 due to not being in time series, results from Airoldi and Christakis (2024), who intervene in a population to induce social contagion, showed large increases in the behavioural adoption for certain treatments when the targeted fraction reached 20 %–30 % of the population. As previously mentioned, several concepts identified in the literature repeatedly appeared across multiple papers, with consistent supporting evidence across different disciplines. In Table 5, we synthesise some higher-level takeaways in more general and less technical language.

Table 5 Key characteristics affecting social tipping processes on networks as identified by their frequency in the literature.

5 Discussion and conclusion

Although complex contagion dynamics in networks are generally not amenable to reductionist methods of analysis (Shalizi and Thomas, 2011), our results show a broad level of agreement with the literature we reviewed regarding variables that affect the success of contagion. Clustering and structure in network topology dominate among these, as does a high degree of trust between social connections (Fig. 4). These factors are also critical in instances where norm change is difficult, payoffs for switching norms are low, social pressure from the in-group exists, or the norm is connected to social identity (Efferson et al., 2020). This is particularly relevant as existing societal norms increasingly conflict with planetary boundaries (Otto et al., 2020b). A particularly relevant issue is the strong tie of group identity to problematic behavioural norms, which stymie the endogenous spread of social norms even after a targeted intervention (Efferson et al., 2020; Ehret et al., 2022). In light of climate change, these behavioural norms could correspond to things such as driving a large car, flying, or eating meat (Peattie, 2010). Social tipping points research in SES calls for leveraging social tipping points to promote rapid societal change (Milkoreit, 2023; Winkelmann et al., 2022). However, it could better address whether tipping is even possible for certain behavioural norms or what dynamics are required for particularly recalcitrant or sensitive norms. Our review shows clearly that each norm change is highly dependent on the social context, distribution of individual preferences, and heterogeneity. It also shows that a high variance in the distribution of personal preferences (social polarisation) is detrimental to changing social norms, which is an increasingly pressing issue (Frei et al., 2023).

Despite these considerations, we observed a clear non-linear trend when we investigated the critical mass required to induce tipping in a social network (Fig. 5). More concretely, we display evidence that a critical mass of around 25 % of the population can precipitate a population-wide social tipping event. This finding is in line with existing speculations about critical mass estimates (Centola et al., 2018). The reason for this is not addressed in detail here, but recent analytical work (Oliveira et al., 2024) suggests that, under a 25 % threshold, homophily limits the interaction potential of minorities, resulting in a “homophily trap”. Not all social systems we analysed demonstrated social tipping (Fig. 5a), even when they displayed a rapid change in the fraction of norm adopters around 25 %. This again highlights that the 25 % threshold identified in this paper is contextually dependent and reflects existing claims about the conditionality of social tipping (Constantino et al., 2022; Winkelmann et al., 2022). A universal critical mass is not guaranteed. However, for the purposes of this study, our results answer our research question: they support the potential existence of a Pareto effect in social tipping dynamics. Although this finding should not be generalised to all social norms, behaviours, and social systems, it is a helpful indicator and target if policymakers would like to engender or monitor wide-scale social change. A potential case is the increasing popularity of vegetarianism in Germany. Figures currently show the vegetarian population to be at around 10 % (Statista, 2024). A more generalisable result of our analysis is shown in Fig. 5b, which gives an estimate of the lower and upper ranges where tipping may occur.

The good agreement between empirical evidence and modelling results identified in this work supports the predictive power of models to investigate complex social contagion processes. This is particularly positive, as each of the modelling results shown in Fig. 5 used different types and forms of models. These modelling approaches must be empirically validated before they can be included in high-level or integrated modelling frameworks such as in IAMs (Trutnevyte et al., 2019). To introduce social complexity into larger models (Donges et al., 2020), validation across modelling approaches may guide less computationally intensive models without losing accuracy. An example is the sigmoid norm adoption curve, as shown in Fig. 1b. This type of function is commonly used in system dynamics models to govern the rates of norm adoption, where the location of the inflection point is an important driver of large-scale social change in some contexts (Eker et al., 2019). There are several avenues to compare this norm adoption curve across methodological approaches, particularly from the network models or norm adoption time series analysed in this work. As a first approximation, this function could be parametrised using the data provided in this analysis (Fig. 5). More broadly, these norm adoption curves can be analytically derived from agent-based network models using approximation methods (Wiedermann et al., 2020) or reconstructed using time series from social media data, e.g. online service adoption (Karsai et al., 2016). A key issue affecting this analysis was the small sample size, particularly with respect to the tipping point results discussed in Sect. 4. The dimensionality, heterogeneity, and scale of variables relating to complex contagion in social networks across disciplines are such that it becomes prohibitively more difficult to process, categorise, and harmonise the findings across disciplines. In this sense, our work should be regarded as an agenda-setting narrative review and by no means as an exhaustive survey of the literature.

While expanded statistical validation remains necessary, our analysis points to several other critical areas for future investigation in social tipping dynamics: for example, research could be conducted in areas where agreement within the discipline is lacking, e.g. for factors like network connectivity, population size, and/or global information (see Fig. 4). The application of the second derivative to characterise tipping points serves as a useful initial approximation. However, its efficacy is contingent upon integration with additional criteria, such as those delineated in the definition of a social tipping event (Box 1). Future research should prioritise two avenues: (1) providing a robust theoretical justification for the use of the second derivative in this context and (2) replicating the analysis using alternative frameworks, such as the criticality approach discussed in Sect. 2.1, or dynamical systems theory (Ritchie et al., 2023). These efforts would serve to validate or refine the current methodology and potentially offer new insights into the dynamics of social tipping points

Beyond methodological refinements, several theoretical challenges remain to be addressed: we only considered a one-dimensional aspect of social tipping, namely its reliance on critical mass as a time-dependent variable. Additionally, we neglected multistability and assumed that there was no intermittent or regressive behaviour of the system once it had been tipped, which is a substantial issue to consider (Ferraz de Arruda et al., 2023). Future work could examine the interaction between multiple stable states, network topology, and node heterogeneity. Although we attempted to address most common network topologies, we decided that multi-layer networks were mostly beyond the scope of this review due to the added complexity normally associated with these approaches. Higher-level network structures have a non-trivial effect on contagion dynamics (De Domenico, 2023; Zhang et al., 2023), and the field of social tipping and social contagion would generally benefit from a comparison between these structures and typical or single-layer network structures.

Many of the reviewed models are not always integrated into broader SES systems: either energy use, emissions, or environmental behaviour are absent. Work should be directed towards reconciling or refining this gap between conceptual frameworks and integrated modelling, where more generic tipping dynamics are included in an SES model. Recent global SES models or World–Earth models (WEMs), which explicitly simulate social dynamics on a micro scale (Donges et al., 2020) and contributions from ecological economics (Lamperti et al., 2018), are good starting points.

The temporality of network processes, such as burstiness (see Sect. 2.6), is important for social tipping but was not fully addressed in our analysis. Two aspects warrant closer investigation: timescale invariance and rate-dependent processes. Firstly, we observed similar tipping dynamics across timescales in our results. Given that timescale invariance is seen in diverse human behaviours (Proekt et al., 2012), future research should systematically investigate whether and under what conditions this property emerges in social tipping processes. Secondly, rate-induced-tipping (R-tipping) analysis could identify critical rates of processes like network reorganisation (rewiring frequency) or adoption frequency that could trigger social tipping even when threshold conditions suggest stability (Ritchie et al., 2023). Particularly crucial for future work is the systematic investigation of conditions under which social tipping occurs at different critical mass thresholds. While our analysis suggests a common range around 20 %–25 %, more understanding is needed of contextual factors that might shift this threshold substantially or preclude tipping dynamics entirely. Such insights are valuable for both theoretical development and practical applications in promoting sustainable behavioural change.

Our macroscopic approach towards measuring tipping thresholds provides concrete critical mass ranges required to facilitate social tipping events via social networks. Where causality was deemed important, we supplemented this more approximate range with an investigation of the factors contributing to social tipping. Our focus on complex contagion and recalcitrant norm change means that our recommendations aid the navigation of inherently difficult societal transitions, such as the one to net-zero. On the flip side, in situations where the norm change is minor and possible, our range of tipping thresholds provides a concrete, empirically supported target for policymakers, encouraging the spread of easier-to-swallow sustainable norm change in social groups.

Appendix A

Table A1 A glossary of terms relevant to our literature review and analysis which may provide the reader with additional context for understanding Figs. 5 and 6 in the main text.

Appendix B

Figure B1 A range of individual tipping thresholds which allow a social tipping event in a given population.