Continental heat storage: contributions from the ground, inland waters, and permafrost thawing

Heat storage within the Earth system is a fundamental metric for understanding climate change. The current energy imbalance at the top of the atmosphere causes changes in energy storage within the ocean, the atmosphere, the cryosphere, and the continental landmasses. After the ocean, heat storage in land is the second largest term of the Earth heat inventory, affecting physical processes relevant to society and ecosystems, such as the stability of the soil carbon pool. Here, we present an update of the continental heat storage, combining for the first time the heat in the land subsurface, inland water bodies, and permafrost thawing. The continental landmasses stored 23.8 ± 2.0 × 10²¹ J during the period 1960–2020, but the distribution of heat among the three components is not homogeneous. The sensible diffusion of heat through the ground accounts for ∼90 % of the continental heat storage, with inland water bodies and permafrost degradation (i.e. latent heat) accounting for ∼0.7 % and ∼9 % of the continental heat, respectively. Although the inland water bodies and permafrost soils store less heat than the solid ground, we argue that their associated climate phenomena justify their monitoring and inclusion in the Earth heat inventory.

1 Introduction

Anthropogenic changes in atmospheric composition have contributed to sustaining the positive radiative imbalance measured at the top of the atmosphere, leading to an accumulation of heat within the Earth system (Levitus et al., 2005; Church et al., 2011; Hansen et al., 2011; von Schuckmann et al., 2020; Forster et al., 2021). The ocean, atmosphere, cryosphere, and continental landmasses have shown a marked increase in heat storage since the 1960s, with the ocean accounting for about 89 % of the total heat storage, the continental subsurface accounting for 6 %, the cryosphere (glaciers, ice caps, sea ice, ice shelves) accounting for 4 %, and the atmosphere accounting for 1 % (von Schuckmann et al., 2020). Continental heat storage has ranked as the second largest term of the Earth heat inventory, only after the ocean in previous works, showing similar values to the heat uptake by the cryosphere (Levitus et al., 2005; Church et al., 2011; Hansen et al., 2011; von Schuckmann et al., 2020). These previous analyses included estimates of heat storage within the global subsurface retrieved from inversions of temperature–depth profiles measured around the world (Beltrami et al., 2002; Cuesta-Valero et al., 2021c). Subsurface temperature profiles record long-term changes in the surface energy balance as perturbations of subsurface temperatures (Beltrami, 2002). If heat diffusion through the ground occurs in a conductive regime, the original changes in ground heat flux at the surface can be retrieved by inverting the measured temperature profiles (Beltrami, 2001; Beltrami et al., 2002; Cuesta-Valero et al., 2021c), from which the ground heat storage can be estimated. Nevertheless, these inversions of subsurface temperature profiles only capture changes in the subsurface thermal regime due to conductive heat diffusion, and other processes should be considered in order to estimate the total continental heat storage.

Phase change in permafrost soils involves the latent heat of the fusion of ice and frozen rocks, and it is not captured in inversions of subsurface temperature profiles; thus, the heat used to thaw ground ice could be a relevant contributor to continental heat storage, at least at higher latitudes. Estimates of permafrost extent, based on current climate conditions, underline 11 % of the global exposed land surface (Obu, 2021), with continuous (cold) permafrost warming by 0.39 ± 0.15 ^∘C and permafrost in the discontinuous zone (warm permafrost) warming by 0.20 ± 0.10 ^∘C between 2007 and 2016 (Biskaborn et al., 2019; Fox-Kemper et al., 2021). Colder permafrost has been warming faster (0.4–0.6 ^∘C per decade) than warmer permafrost (0.17 ^∘C) since 1978 (Gulev et al., 2021). Active-layer thickness is also increasing at most measurement locations around the world (Smith et al., 2022b). Additionally, global climate simulations project a decrease of 10 % to more than 80 % in near-surface permafrost (upper 3 m of the subsurface) extent and a decrease of 25 ± 5 % in total permafrost volume due to thawing by the end of the 21st century, depending on future greenhouse gas emissions (Koven et al., 2013; Slater and Lawrence, 2013; Burke et al., 2020; Hermoso de Mendoza et al., 2020; Fox-Kemper et al., 2021; Steinert et al., 2021). Consequently, substantial latent heat uptake due to ground ice thawing in permafrost-underlain areas is expected for the following decades.

Similarly, a large amount of energy is required to warm lakes, rivers, and artificial reservoirs due to the high heat capacity of water, which may constitute another relevant contributor to continental heat storage not included in previous analyses. Inland surface water bodies extend through a considerable part of the land surface. For instance, natural lakes cover ∼2 % (2 662 040  km²) of the global continental surface (Messager et al., 2016; Vanderkelen et al., 2020). Rivers and lakes have warmed by 1 and 0.45 ^∘C per decade, respectively, in the last 3 decades, resulting in an a reduction of ∼25 % in ice cover, and there is high confidence that these trends are going to continue throughout the 21st century according to the IPCC Sixth Assessment Report (Douville et al., 2021). Furthermore, previous estimates of heat flux in global inland surface water bodies from a multimodel ensemble of simulations yielded ∼121 mW m⁻² (1 mW m${}^{-\mathrm{2}}=\mathrm{0.001}$ W m⁻²) for the period 1991–2020 (Vanderkelen et al., 2020), which is similar to the ground heat flux determined from subsurface temperature profiles.

Here, we quantify the continental heat storage by combining ground heat storage, heat uptake by inland water bodies, and heat used for thawing permafrost. Heat storage from these three components is estimated from 1960 to 2020 and is compared to previous estimates of the Earth heat inventory. These estimates of continental heat storage will contribute to updating the global Earth heat inventory defined in von Schuckmann et al. (2020). We also argue about the importance of monitoring all three components of continental heat storage in the future due to the implications of the changes in heat content within these subsystems for society and ecosystems.

2 Data and methods

2.1 Estimates of ground heat storage

Ground heat fluxes are estimated from deep subsurface temperature profiles, consisting of measurements of temperature with depth usually performed in holes that were drilled for mining prospecting campaigns and that are, thus, unevenly distributed across the global land surface. These profiles are typically described by the following two components: a quasi-equilibrium temperature profile and the propagation of recent variations in the surface energy balance (Beltrami, 2002). The quasi-equilibrium profile corresponds to the temperature profile in an equilibrium state, that is, with a constant surface temperature and geothermal gradient. Heat flow from the Earth interior is constant at temporal scales of millions of years; thus, the local geothermal gradient can be considered to be constant (Jaupard and Mareschal, 2010). However, recent changes in total radiation reaching the land surface (Wild et al., 2015) ensure that local surface temperatures are not constant in the long term. A common approach to estimating the quasi-equilibrium profile consists of performing a linear regression analysis of the deepest part of each profile, as this is the part least affected by recent changes in surface conditions (Cuesta-Valero et al., 2019). Thereby, the geothermal gradient is assumed to correspond to the slope of this regression line, while the extrapolation of the fitted line to the surface is considered to be the long-term past surface temperature. Variations of the surface energy balance are assumed to propagate into the ground following the one-dimensional heat diffusion equation, and these are recorded in the profile as alterations to the quasi-equilibrium profile (Carslaw and Jaeger, 1959). Therefore, this signature of changes in surface conditions on subsurface temperatures can be estimated by subtracting the quasi-equilibrium profile from the measured log, obtaining an anomaly profile. Ground heat flux histories retrieved in this analysis are based on inverting the anomaly profile of each individual subsurface temperature profile.

We invert subsurface temperature profiles from the Xibalbá dataset (Cuesta-Valero et al., 2021c, a) to estimate the global long-term ground heat flux history. The Xibalbá dataset consists of 1079 subsurface temperature profiles measured around the world, with a larger number of profiles in the middle latitudes of the Northern Hemisphere. The Xibalbá profiles have been screened by eye to remove logs including non-climatic signals due to processes such as water advection (Cuesta-Valero et al., 2021c). The logs have also been harmonized to include temperature records from depths of 15 to 300 m. Ensuring that all logs are truncated at the same depth is crucial to obtaining temperature and heat flux estimates relative to the same temporal reference, which, in this analysis, approximates the period 1300–1700. This period of reference arises from the depth range (in this case, 200–300 m) used to perform the linear regression analysis from which the corresponding quasi-equilibrium temperature profile from each individual log is determined. Additionally, a homogeneous subsurface with a constant thermal diffusivity of $\mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{6}}$ m² s⁻¹ is considered in order to derive this temporal reference (see Cuesta-Valero et al., 2019, for details about the relationship between depth range and the period of reference). Once the quasi-equilibrium profile is estimated, the corresponding anomaly profile is retrieved as explained above.

Ground surface temperature histories are estimated from individual Xibalbá profiles using a singular value decomposition (SVD) algorithm (Lanczos, 1961) to invert each anomaly profile. Inversions performed by this SVD algorithm are common in the literature (Beltrami and Mareschal, 1992; Mareschal and Beltrami, 1992; Clauser and Mareschal, 1995; Beltrami et al., 2015; Jaume-Santero et al., 2016; Pickler et al., 2016) and have shown robust results in experiments designed to test their ability to retrieve past changes in global surface temperature (González-Rouco et al., 2006, 2009; García-García et al., 2016; Melo-Aguilar et al., 2018). Ground heat flux histories are then retrieved from each ground surface temperature history using the technique developed in Wang and Bras (1999) from a half-order derivative approach:

$$\begin{array}{}\text{(1)}& G\left(t_N\right)={\displaystyle \frac{\mathrm{2}\mathit{\lambda }}{\sqrt{\mathit{\pi }\mathit{\alpha }}}}\sum _k^{N-\mathrm{1}}{\displaystyle \frac{T_{k+\mathrm{1}}-T_k}{t_{k+\mathrm{1}}-t_k}}\left(\sqrt{t_N-t_k}-\sqrt{t_N-t_{k+\mathrm{1}}}\right),\end{array}$$

with α being the thermal diffusivity of the medium, λ being the thermal conductivity, G(t_N) being the ground heat flux at the time t_N, T_k being the ground surface temperature history at the k-th time step, and t_k being the time at the k-th time step. This approach has been used extensively in the literature to derive global ground heat flux histories and has shown good results when compared to other techniques (Beltrami, 2001; Beltrami et al., 2002; Bennett et al., 2008; Cuesta-Valero et al., 2021c). Here, we consider thermal diffusivities ranging from $\mathrm{0.5}\times {\mathrm{10}}^{-\mathrm{6}}$ to $\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{6}}$ m² s⁻¹ and thermal conductivities between 2.5 and 3.5 W m⁻¹ K⁻¹ to perform the inversions and to estimate ground heat flux histories, which are typical values in the literature.

These SVD inversions are combined with a bootstrap sampling strategy to retrieve the 2.5th, 50th, and 97.5th percentiles of the spatially aggregated heat flux histories (Efron, 1987; DiCiccio and Efron, 1996; Davison and Hinkley, 1997). The bootstrap method consists of estimating global mean ground heat fluxes from populations of 1079 elements (i.e. the number of Xibalbá profiles), with each element being a ground heat flux history from a Xibalbá profile retrieved using randomly selected values for thermal diffusivity and thermal conductivity (see ranges above), as well as a random quasi-equilibrium temperature profile. This random quasi-equilibrium profile is chosen from the Gaussian distribution of long-term mean surface temperature and geothermal gradient retrieved from the linear regression analysis performed in the deepest 100 m of the corresponding profile, as explained above. This process is repeated 1000 times to obtain an ensemble of global heat flux averages, considering the 50th percentile of the ensemble to be the best estimate of global ground heat flux and the 2.5th and 97.5th percentiles to be the 95 % confidence interval. A detailed description of the bootstrapping sampling approach combined with the SVD algorithm can be found in Cuesta-Valero et al. (2022).

Ground heat storage is estimated as the accumulated heat flux since 1960 considering the global land area without Greenland and Antarctica (1.34×10¹⁴ m²), as there are no measured profiles in these areas. As indicated in Cuesta-Valero et al. (2021c), removing other land areas such as northern and middle Africa, South America, and the Middle East does not affect the results much. Furthermore, several studies have shown that the current spatial distribution of subsurface temperature profiles is enough to capture the global change in surface conditions (González-Rouco et al., 2009; García-García et al., 2016; Melo-Aguilar et al., 2020; Cuesta-Valero et al., 2021c). Since the number of measured profiles decreases sharply after 2000, we extrapolate the trend of ground heat flux for the period 1970–2000 to fill the period 2000–2020 with data, as in von Schuckmann et al. (2020).

2.2 Estimates of permafrost heat storage

Heat storage within the continental subsurface is also used for ground ice melting as permafrost temperatures approach 0 ^∘C. However, estimates of ground heat storage from subsurface temperature profiles cannot recover the latent heat flux used for permafrost thawing. These estimates of latent heat flux, permafrost heat flux hereinafter, are physically and methodologically different to estimates of sensible heat flux, referred as ground heat flux in this article. Latent heat stored in permafrost due to melting of ground ice is estimated from extensive parameter ensemble simulations using the CryoGridLite permafrost model (Langer et al., 2022; Nitzbon et al., 2022). The model uses an implicit, iterative, backward Euler scheme to solve the heat transfer equation with phase change in mixed enthalpy form (Swaminathan and Voller, 1992). Daily average enthalpy and liquid water content profiles are calculated to a depth of 550 m with a spatial resolution of 1^∘ (per grid cell) for the Arctic permafrost region. The surface temperature offset caused by snow insulation is represented by a dedicated snow scheme accounting for regional snow characteristics (Sturm et al., 2010). Ground stratigraphies which determine both the thermal properties of the ground and the amount and location of ground ice are derived based on soil stratigraphy parameterizations developed for the SURFEX land surface model (Masson et al., 2013). Required input data are extracted from multiple global datasets, such as the percentage of sand and clay in the soil (Masson et al., 2003; Faroux et al., 2013), the soil organic carbon content (Hugelius et al., 2013), and the soil thickness (Pelletier et al., 2016).

Uncertainties in soil stratigraphies affecting latent heat storage are primarily determined by the amount and distribution of ground ice. Such uncertainties are accounted for by ensemble parameter simulations (N=100) using a Monte Carlo approach that randomly varies soil thickness and the thickness of soil layers with different levels of ice saturation (Langer et al., 2022; Nitzbon et al., 2022). The presence of excess ice was considered by increasing the ground ice content for 50 % of the ensemble members according to the information provided in the map by Brown et al. (1997). Specifically, we increased the ground ice content in the uppermost 10 to 20 m uniformly by an amount according to the low, medium, and high ice content classes given in the map (see Nitzbon et al., 2022, for details). The climate forcing of the simulations performed is based on daily mean surface temperatures and daily snowfall amounts. The climate forcing used is a synthetic time series combining Commonwealth Scientific and Industrial Research Organisation (CSIRO) paleoclimate simulations (500 CE–1979) based on the Mk3L climate system model (Phipps et al., 2013) with reanalysis data (1979–2019) based on ERA-Interim (Dee et al., 2011). Both climate time series are harmonized using an anomaly approach to extend the last decade of the reanalysis data into the past. The lower boundary condition at 550 m depth is set to a local geothermal heat flux according to the global map of solid earth surface heat flow (Davies, 2013). Here, the period from 500 CE to 1960 is considered sufficient to bring the model to dynamic equilibrium after initialization with steady-state conditions (averaged for 500 to 600 CE).

The results of the simulations are analysed by integrating the daily liquid soil water content profiles with depth to obtain the total average annual liquid water content per square metre. Multiplying this water content by the volumetric latent heat of fusion of water (334×10⁶ kJ m⁻³) yields the average annual latent heat uptake per square metre, which is multiplied with the land area (excluding the surface water area) contained within each model grid cell. The uncertainties caused by uncertain ground ice distributions are provided as average standard deviation calculated from the ensemble. The CryoGridLittle model has been previously evaluated against measurements of ground surface temperatures at 82 different stations of the Global Terrestrial Network for Permafrost (GTN-P) covering the period 2007–2016 (Langer et al., 2022). The root mean squared error between the simulated and measured temperatures is 2.2 ^∘C for the entire dataset, with a warm bias of 0.6 ^∘C, a performance comparable to or better than other model analyses (Langer et al., 2022).

Subin et al. (2012)Goudsmit et al. (2002)Tan et al. (2015)Sachse et al. (2014)

Table 1 Overview of global lake models used. Detailed descriptions of the models and modelling setup can be found in Golub et al. (2022).

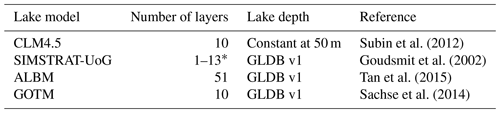
^∗ The number of lake layers used in SIMSTRAT-UoG varies spatially and depends on the mean lake depth of the grid cell.

2.3 Estimates of inland-water heat storage

The heat storage by inland waters, including natural lakes, reservoirs, and rivers, is estimated for the period 1900–2021 by combining water temperature anomalies with volume estimates. To this end, we use a combination of global-scale lake models, global hydrological models, and Earth system model (ESM) simulations from the Inter-Sectoral Impact Model Intercomparison Project phase 2b (ISIMIP2b, Frieler et al., 2017; Golub et al., 2022), with the methods described in Vanderkelen et al. (2020). To derive lake temperature profiles, we expand the global lake model ensemble consisting of three global lake models (CLM45, ALBM, and Simstrat-UoG), each providing simulations driven by bias-adjusted atmospheric forcing from four ESMs (GFDL-ESM2M, HadGEM2-ES, IPSL-CM5A-LR, and MIROC5), with four simulations using an additional global lake model, the General Ocean Turbulence Model (GOTM; Sachse et al., 2014), driven by the same ESMs. In total, the ensemble contains 16 global lake simulations, providing lake temperature profiles (Table 1) for the period 1900 to 2021 on a 0.5^∘ by 0.5^∘ grid. These simulations are combined with global gridded lake depths from the Global Lake Database v.3 (GLDB; Choulga et al., 2019) rasterized global lake and reservoir area from HydroLAKES and GRanD databases (Messager et al., 2016; Lehner et al., 2011), as described in Vanderkelen et al. (2020).

Differently from the cylindrical-lake assumption of Vanderkelen et al. (2020), in which the grid cell lake volume is calculated by multiplying lake area and depth, we determine lake and reservoir volumes by estimating lake morphometry with the volume development parameter (V_d), which is a well-established geometric approach (Håkanson, 1977; Johansson et al., 2007). The V_d parameter represents the extent to which the lake volume deviates from the volume of a cylinder, thereby indicating whether the lake morphometry is concave or convex. We employ a global constant V_d value of 1.19, which is the median V_d derived from the 1 427 688 lake polygons in the GLOBathy dataset (Khazaei et al., 2022) using their mean and maximum depths $\left(V_{\text{d}}=\mathrm{3}\cdot {\displaystyle \frac{d_{\text{mean}}}{d_{\text{max}}}}\right)$. Per grid cell, the lake volume is calculated as a “reversed wedding cake” by multiplying the thickness of every discrete lake layer of the lake model with the average area at the layer depth A(z), calculated following Johansson et al. (2007) as follows:

$$\begin{array}{}\text{(2)}& A\left(z\right)=A_{\text{max}}{\left[\left(\mathrm{1}-d_{\text{ref}}\right)\left(\mathrm{1}+d_{\text{rel}}\sin \left(\sqrt{d_{\text{rel}}}\right)\right)\right]}^{f_{V_{\text{d}}}},\end{array}$$

and

$$\begin{array}{}\text{(3)}& f\left(V_{\text{d}}\right)=\mathrm{1.7}{V}_{\text{d}}^{-\mathrm{1}}+\mathrm{2.5}-\mathrm{2.4}{V}_{\text{d}}+\mathrm{0.23}{V}_{\text{d}}^{\mathrm{3}},\end{array}$$

with A_max (m²) being the surface lake area calculated based on the gridded HydroLAKES distribution; d_rel (m) being the relative lake layer depth $\left(d_{\text{rel}}=\frac{z}{z_{\text{max}}}\right)$, where z_max (m) is given by the GLDB lake depth; and finally, V_d (−) being the volume development parameter, taken as constant at 1.19.

Then, the lake heat content of every grid cell is calculated by combining the volume of every lake layer with the layer temperature and integrating it over the whole lake column. Next, the heat storage is computed from the globally aggregated lake heat content values relative to the year 1960. To estimate heat uptake by reservoirs, we not only account for warming temperatures but also include the increase in water volume through reservoir construction by using transient reservoir area, in which reservoirs appear in their year of construction given by GRanD (Vanderkelen et al., 2021, 2022). Finally, heat flux estimates are derived from the heat content time series by calculating the difference in heat content between 2 consecutive years divided by the total lake and reservoir area for the corresponding years.

The provided best estimate and uncertainty range for inland-water heat storage and heat flux is given as the mean and standard deviation of the multimodel ensemble of the 16 simulations described above.

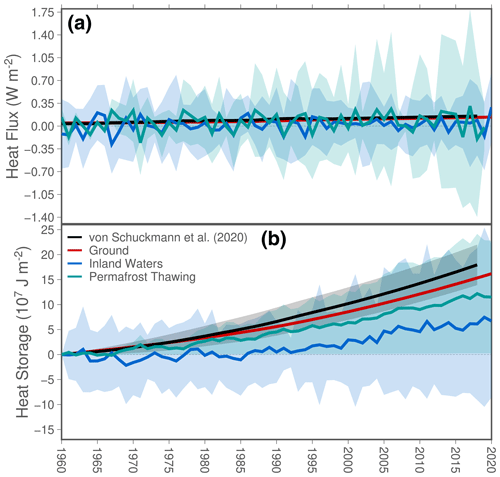
Figure 1 Global heat flux (a) and global heat storage per unit of area (b) from the ground (red lines), inland water bodies (blue line), and permafrost thawing (green line) for the period 1960–2020. Black lines indicate ground heat fluxes and ground heat storage from von Schuckmann et al. (2020). Please, note that ground estimates consist of long-term changes of heat flux and heat storage and do not include interannual variability.

3 Results

Estimates of ground heat flux by the new bootstrapping technique described above present smaller values and a narrower uncertainty range than the results from previous estimates using the Xibalbá dataset (von Schuckmann et al., 2020; Cuesta-Valero et al., 2021c). Previous analyses presented a global heat flux of 97±6 mW m⁻² for 1960–2018 in comparison with 84.8±0.8 mW m⁻² for the period 1960–2020 in this study (Fig. 1a). Both heat flux estimates consider the same subsurface temperature profiles and the same singular value decomposition algorithm to produce inversions of individual logs. Nevertheless, the new bootstrap method used to aggregate inversions from individual profiles is conceptually different from the aggregation method used in von Schuckmann et al. (2020), which leads to slightly different values of global ground heat flux and to a narrower 95 % confidence interval (Cuesta-Valero et al., 2022). The large difference between the previous and the new uncertainty estimates arise due to the incorrect aggregation technique used in previous studies, which was flawed towards unrealistically large values. The singular value decomposition method in von Schuckmann et al. (2020) is based on deriving two extremal inversions from each individual profile and then considering the global uncertainty as the average of these extremal inversions. The bootstrap approach, nevertheless, derives a set of 1000 different global averages from individual profiles considering a different quasi-equilibrium profile and a different thermal diffusivity each time, retrieving the 2.5th, 50th, and 97.5th percentiles of these global averages. The new bootstrap approach, therefore, should be considered to be a better method for aggregating inversions from different temperature profiles. A more detailed comparison between these two aggregation techniques can be consulted in Cuesta-Valero et al. (2022). The ground heat fluxes from the bootstrap inversion technique are also higher than those from Beltrami et al. (2002), which presented 39.1 mW m⁻² for 1950–2000. These large differences between our results and those from Beltrami et al. (2002) arise from the use of different inversion methods and from the higher number of more recent subsurface temperature profiles in the Xibalbá dataset than in Beltrami et al. (2002), thus including the recent warming of the continental subsurface. Heat flux for inland water bodies reaches 16±27 mW m⁻² for 1960–2020, displaying a large interannual variability and multimodel spread (Fig. 1a). This large interannual variability in comparison with estimates of ground heat flux and permafrost heat flux is explained by the smaller surface of global lakes and reservoirs in comparison with the global land and permafrost areas, concretely 2 and 1 orders of magnitude smaller than the land and permafrost areas. Permafrost heat flux estimates for the Arctic region yield 60±80 mW m⁻² for the period 1960–2020, thus being lower than that of the ground and higher than that of inland water bodies during the same period of time. All three components present positive heat flux trends, with ground heat flux presenting a trend of 1.7 mW m⁻² yr⁻¹, inland water bodies showing a trend of 1.3 mW m⁻² yr⁻¹, and the trend for permafrost heat flux amounting to 0.9 mW m⁻² yr⁻¹. Ground heat flux data after the year 2000 are an extrapolation of the 1970–2000 trend, which could imply an underestimation of the trend for the whole period due to the fast change in global surface temperatures in recent times (Gulev et al., 2021).

Estimates of heat storage per unit of area show large differences in the capacity of each subsystem to gain heat (Fig. 1b), with the ground displaying a heat storage of 161.9±0.7 MJ m⁻² (1 MJ = 10⁶ J), inland water bodies displaying a heat gain of 67±76 MJ m⁻², and permafrost soils displaying a heat gain of 115±56 MJ m⁻² at the end of the period 1960–2020 (Fig. 1b). There are also spatial differences in the retrieved heat storage per unit of area, with a general heat gain in inland water bodies and subsurface temperature profiles around the globe but with most permafrost heat gains arising from southern Arctic latitudes (Fig. 2). Subsurface temperature profiles show a general increase of heat content in the ground, although with individual logs displaying heat losses at certain locations (Fig. 2a). However, individual profiles are sensitive to microclimate conditions (e.g. Taylor and Wang, 2008); thus, signals at individual locations may vary in comparison with the regional pattern. Regional differences appear in the heat storage per unit of area in inland water bodies (Fig. 2b), showing a general heat gain except in Southeast Asia and in the southwestern shore of Hudson Bay in Canada. After examining these two areas more in detail and after a literature review, we cannot provide an explanation for these heat loses in inland waters heat storage at this moment. Permafrost soils display small changes in terms of heat content in northern Canada, northern Alaska, and most of Siberia in contrast to a strong heat gain in the southern part of the Arctic region in North America and Asia (Fig. 2c).

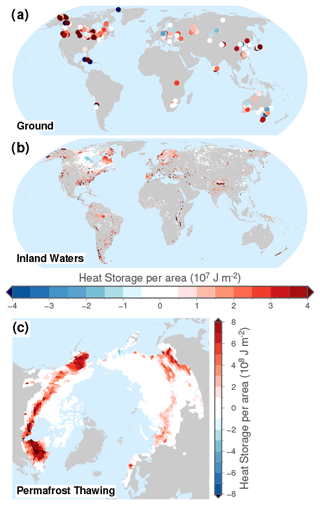
Figure 2 Spatial distribution of heat storage per unit of area since 1960 for (a) ground heat storage from subsurface temperature profiles measured after 1990, (b) heat storage from inland water bodies, and (c) heat storage from permafrost thawing. Please note the different scale for permafrost heat storage.

The estimates of heat flux and heat storage per unit of area for inland water bodies are derived from the total heat storage for natural lakes and reservoirs, similarly to Vanderkelen et al. (2020). These heat storage time series for natural lakes represent the changing water temperatures, which show a positive trend from the 1990s onwards (Fig. 3a). Our estimates, 0.18±0.19 ZJ for 2011 to 2020 relative to past times (1900–1929), are lower compared to previous estimates (0.29 ± 0.2 ZJ for the same period; Vanderkelen et al., 2020). This difference can be attributed to the additional simulations with the global lake model GOTM and the refined volume estimates. Contrary to the other simulations, the GOTM simulations forced by HadGEM2-ES and MIROC5 do not show an upward trend (Fig. S1 in the Supplement). Using the V_d parameter as a measure for lake morphometry to calculate lake layer volumes results in lower volumes compared to using the cylindrical approach. A sensitivity analysis comparing heat storage for natural lakes with different global mean V_d values and the cylindrical approach shows that heat storage increases with increasing V_d values, while the cylindrical bathymetry results in distinctly larger values (Fig. S2 in the Supplement). This can be explained by the different lake volumes which are higher for concave-shaped bathymetries (V_d>1) than for more convex-shaped bathymetries (V_d<1; Johansson et al., 2007). The cylindrical approach results in the highest lake volumes and therefore the largest heat storage. Reservoir heat storage is an order of magnitude smaller compared to natural lakes with estimates of 0.21±0.17 ZJ for 2011 to 2020, relative to past times (Fig. 3b). The steady increase originates from both reservoir construction, which accelerated in the years 1950–1970, and the increasing water temperatures. Finally, Vanderkelen et al. (2020) report river heat storage estimates of −0.36 ± 1.2 ZJ for 2011 to 2020, relative to past times, based on water storage simulations by two global hydrological models within the ISIMIP2b framework and river temperatures derived from surface temperatures of the GCMs. These estimates are characterized by a large uncertainty, which originates from a high variability in water storage, masking the positive temperature trend (Vanderkelen et al., 2020).

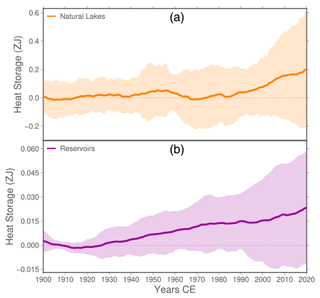
Figure 3 Heat storage by natural lakes (a) and reservoirs (b). Shown are 6-year moving averages relative to the 1900–1929 reference period. Note the different y-axis scales. Colour shades represent the uncertainty range shown as the standard deviation of the used simulations (16 for lake and reservoir heat storage).

The total continental heat storage since 1960 reaches 23.8 ZJ (1 ZJ = 10²¹ J) with a two-σ value of 2.0 ZJ. The uncertainty for permafrost heat storage arises mainly from the unknown soil stratigraphies in the Arctic, with the uncertainty for inland waters heat storage arising mostly due to structural differences in the models considered to derive the estimates. Nevertheless, the uncertainty ranges from the different continental subsystems include markedly different factors due to the different sources of information considered in the analysis. The uncertainty for ground heat storage arises from unknown subsurface thermal properties and from the determination of the quasi-equilibrium profile at each location. The uncertainty for permafrost heat storage arises mainly from the unknown soil stratigraphies in the Arctic, with the uncertainty for inland waters heat storage arising mostly due to structural differences in the models considered to derive the estimates. Therefore, we cannot provide a robust uncertainty estimate for the total continental heat storage, and future iterations of this analysis should focus on harmonizing the estimates of uncertainty in the individual components in order to enhance the total uncertainty in continental heat storage.

The total continental heat storage is distributed over the different components as follows: 21.6±0.2 ZJ is stored in the ground, 0.2±0.4 ZJ is stored in inland water bodies, and 2±2 ZJ is used to thaw permafrost during the period 1960–2020. This value of continental heat storage, including the storage in the ground, in water bodies, and in permafrost thawing, is nevertheless similar to the previous value of ∼24 ZJ published in von Schuckmann et al. (2020) for the period 1960–2018. This similar value is reached due to the inclusion of permafrost heat storage and inland waters heat storage, since the ground heat storage estimated here is smaller than the value reported in von Schuckmann et al. (2020), as discussed above (see Cuesta-Valero et al., 2022, for a detailed analysis). In any case, the new estimate is within the 95 % confidence interval provided in von Schuckmann et al. (2020). Ground heat storage accounts for the majority of continental heat, representing more than 90 % of the continental heat storage for the period 1960–2020 (Fig. 4); inland water bodies store ∼0.7 %, and permafrost thawing accounts for approximately 9 %. Nevertheless, our estimates of permafrost heat storage do not include the thawing of ground ice in the Tibetan Plateau; thus, the percentage corresponding to permafrost in Fig. 4 is probably larger than the value presented here.

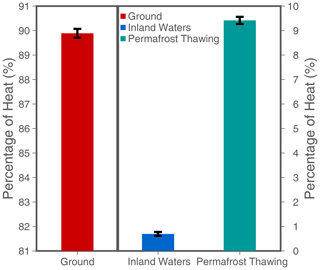
Figure 4 Percentage (%) of the continental heat storage within each analysed land component for the period 1960–2020: ground (red), inland water bodies (blue), and permafrost thawing (green). The left axis corresponds to ground results, and the right axis corresponds to results for permafrost soils and inland water bodies.

4 Implications for society and ecosystems

Global climate models project a warming of the Earth system in the near future, even under low-emission scenarios (Tokarska et al., 2020; IPCC, 2021). These projections imply an increase in the amount of continental heat storage together with an amplification of a series of impacts on society and ecosystems (Fig. 5). Energy exchanges between the lower atmosphere and the shallow subsurface determine the energy balance at the land surface, which connects the changes in net radiation, sensible heat flux, latent heat flux, and ground heat flux (Bonan, 2002). As part of the land surface energy balance, and despite being the smallest term in most situations (Bonan, 2002; Purdy et al., 2016), ground heat flux needs to be determined in order to close the energy balance at the surface and to minimize uncertainties in the rest of the components. A complete knowledge of the surface energy balance, together with soil conditions, is fundamental to understanding the evolution of land–atmosphere interactions affecting important climate and meteorological phenomena, such as surface temperature increases, surface temperature variability, and extreme temperature events (Seneviratne et al., 2006; Fischer et al., 2007; Seneviratne et al., 2013; Thiery et al., 2017; Vogel et al., 2017; Ma et al., 2018; Wang et al., 2022; Parmesan et al., 2022).

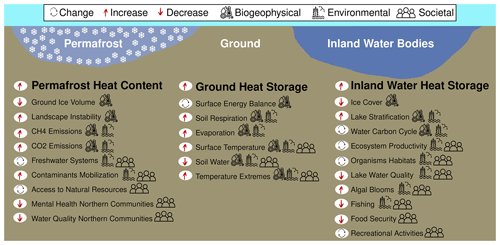
Figure 5 Environmental processes and societal implications affected by changes in heat storage within the continental subsurface (ground), inland water bodies, and permafrost soils. Arrows indicate the direction of change for each process according to the increases in heat storage in the corresponding component of the continental heat storage. See Sect. 4 for more details.

Increases in ground heat storage also produce a warmer subsurface, which threatens the stability of the soil carbon pool by enhancing heterotrophic soil respiration and permafrost thawing, thus increasing emissions of greenhouse gases such as carbon dioxide and methane, particularly from northern soils (Koven et al., 2011; MacDougall et al., 2012; Schädel et al., 2014; Schuur et al., 2015; Hicks Pries et al., 2017; McGuire et al., 2018). Although permafrost heat storage is just 9 % of the continental heat storage, the heat used to thaw permafrost during 1994–2017 (1.49±0.31 ZJ) is comparable to the heat used to melt ground ice in Greenland (1.33±0.11 ZJ) and in ice shelf calving globally (1.24±0.29 ZJ) during the same period of time (Slater et al., 2021). Permafrost heat storage is larger than the heat used to melt Antarctic sea ice and Antarctic ground ice, but it is smaller than the heat uptake by global glaciers and Arctic sea ice melting during 1994–2017. Permafrost thawing is also associated with a powerful biogeochemical feedback, the permafrost carbon feedback, that will add additional greenhouse gases into the atmosphere at a pace of 18 PgC per degree Celsius of global warming by 2100 according to the IPCC 6th Assessment Report (Canadell et al., 2021), affecting the fulfilment of the temperature targets of the 2015 Paris Agreement (Natali et al., 2021). Furthermore, the risk of sudden thawing for carbon-rich zones in the Arctic subsurface, like the Yedoma region and peatland-rich regions, has increased in recent decades (Strauss et al., 2013; Nitzbon et al., 2020; Fewster et al., 2022). The abrupt thaw of ice-rich permafrost, mediated by pond formation and the associated collapse of material around the ponds, may constitute a tipping point for the climate system, mostly due to the release of carbon dioxide and methane and the long lifetime of carbon dioxide in the atmosphere (Lenton, 2012; Turetsky et al., 2019). Although the IPCC Special Report on the Ocean and Cryosphere in a Changing Climate indicates low to medium confidence in surpassing this tipping point in the 21st century (Collins et al., 2019), the consequences of crossing this dangerous threshold for the Earth system could be severe (Lenton et al., 2019). Freshwater systems may be altered by the movement of previously frozen water and associated dissolved contaminant materials, including changes in groundwater storage and in river discharge (Bense et al., 2009; Muskett and Romanovsky, 2009). The health of northern communities can thus be affected by the degradation of this previously stable frozen layer, as contaminants such as radon and others can be released into the local freshwater systems (Furgal and Seguin, 2006; Cochand et al., 2019; Teufel and Sushama, 2019; Ji et al., 2021; Miner et al., 2021; Mohammed et al., 2021; Berry and Schnitter, 2022; Glover and Blouin, 2022). Permafrost thawing is also altering the Arctic landscape due to thermokarst processes, including ground subsidence, ponding of water, slope instability, riverbank instability, and channel widening (Jorgenson and Grosse, 2016; Ardelean et al., 2020). Furthermore, changes in landscape hamper travelling (Gädeke et al., 2021) and increase the maintenance costs of buildings, damaging the mental health of northern communities (Lebel et al., 2022) and threatening industrial structures for the retrieval of natural resources (Buslaev et al., 2021).

Heat uptake by inland water bodies and the associated increase in water temperatures are causing changes in lake ice cover duration and lake stratification, ultimately changing the thermal habitats of organisms and evaporation rates (Wang et al., 2018; Woolway et al., 2020; Grant et al., 2021; Kraemer et al., 2021; Woolway et al., 2021b; Zhao et al., 2022). These changes in the thermal state of inland freshwater systems are affecting ecosystem dynamics by degrading water quality, altering the carbon cycle, and producing algal blooms that alter oxygen concentrations and primary productivity, which in turn threatens the food security of communities relying on freshwater fisheries and other ecosystem services, like recreational activities (McIntyre et al., 2016; Woolway et al., 2020, 2021a; Parmesan et al., 2022).

Therefore, it is clear that all three components of the continental heat storage are relevant for understanding the implications of climate change, independently of the different levels of heat storage estimated here. An analogous situation arises from the analysis of the global Earth heat inventory (von Schuckmann et al., 2020), where the ocean is the leading reservoir of heat, accounting for ∼89 % of the total heat gain in the Earth system. However, changes in heat storage in the continental landmasses, the atmosphere, and the cryosphere are also important due to the associated repercussions for society and ecosystems. For instance, changes in cryosphere heat content account for just 4 % of the total heat gain in the system, but accurately quantifying future heat increases in this climate subsystem is critical for projecting sea level rise. In the same way, permafrost heat storage may be just 9 % of the continental heat storage, but thawing of permafrost soils is a potentially large source of greenhouse gases due to its associated permafrost carbon feedback (Miner et al., 2022). Therefore, it is important to monitor all three components of the continental heat storage.

Table 2 Continental heat storage (CHS) from this analysis and from von Schuckmann et al. (2020) (vS20) in ZJ (1 ZJ = 10²¹ J). Results for ground heat storage (GHS), permafrost heat storage (PHS), and inland waters heat storage (IWHS) are also displayed.

5 Conclusions and future steps

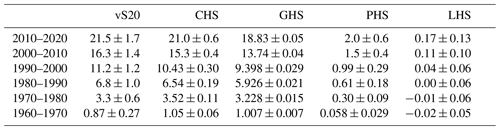
Continental heat storage has been estimated here by considering, for the first time, inland water bodies and permafrost thawing in addition to the land subsurface. All three components present heat gains during the period 1960–2020, with total heat storage increasing more in the last decades of this period (Table 2). Determining the continental heat storage from all land components is important to accurately quantify the Earth heat inventory, which is the critical magnitude informing us about future warming and climate change (von Schuckmann et al., 2020), as well as to provide us with an indicator of the heat-dependent impacts on society and ecosystems (Fig. 5). Monitoring the evolution of continental heat storage and its three subsystems is, therefore, important, and periodic updates of this analysis are planned at a frequency of 2–3 years in order to incorporate new data and techniques.

Certain aspects of the analysis presented here should be improved in future iterations. New measurements of subsurface temperature profiles are crucial to providing ground heat flux estimates for the last 2 decades of the period of interest. Values of ground heat flux from 2000 to 2020 in this analysis consist of an extrapolation due to the lack of sufficient profiles measured after the year 2000. Also, new measurements in the Southern Hemisphere and the Middle East are necessary to characterize areas without coverage in the global network of subsurface temperature profiles. Ideally, an international organization should gather a copy of all available measured subsurface temperature profiles to ensure the maintenance and accessibility of these valuable records in future decades. Such a safe copy of all logs should lead to less-fragmented datasets, harmonizing the archiving practices and metadata requirements for all records, in contrast to current practices in which individual researchers are responsible for measuring, curating, storing, and distributing the data.

Several limitations are also present in our estimate of permafrost heat storage. The primary source of uncertainty in this analysis is the lack of accurate information about the amount and distribution of ground ice in permafrost regions. Additionally, the Tibetan Plateau, the Alpine regions, and the Southern Hemisphere are not included in the analysis; thus, the heat storage by melting of ground ice is probably slightly larger than the values presented here. Since it can be assumed that there is substantially more ground ice in the Arctic region than in the other regions (Zhang et al., 2008), only a small portion of the permafrost heat reservoir is likely to be missing. Among the limitations of the permafrost model are neglected modes of permafrost thaw, such as thermokarst and thermo-erosion. Furthermore, the model does not represent ground subsidence, a dynamic ground hydrology, and processes occurring at subgrid resolution. The absence of these processes affects the representation of the insulating capacity of the active-layer thickness and likely leads to an underestimation of permafrost thaw (Lee et al., 2014; Rodenhizer et al., 2020; Smith et al., 2022a). Most of these limitations arise from the need to perform long-term simulations of permafrost evolution. Therefore, the computational effort, the availability of input data, and the process representation have to be balanced. Including the Tibetan Plateau and the permafrost zones of Antarctica should be possible in the near future, as those require a modest increase in computational resources and input data to derive soil stratigraphies.

Estimates of continental heat storage can potentially be used to constrain and evaluate transient climate simulations performed by global climate models. The Earth heat inventory has already been used to evaluate historical simulations from the fifth phase of the Coupled Model Intercomparison Project (CMIP5), showing that these models present issues in terms of representing a realistic distribution of stored heat among the different climate subsystems, as well as some energy conservation issues (Cuesta-Valero et al., 2021b). The same analysis indicates that the shallow continental subsurface represented in the land surface model (LSM) components is one of the main reasons for their biased representation of the heat inventory. Such a result is in agreement with previous analyses comparing ground heat flux and ground heat storage from subsurface temperature profiles and climate simulations, which has lead to the development of deeper LSMs (MacDougall et al., 2008, 2010; Cuesta-Valero et al., 2016). Furthermore, this deeper subsurface in LSMs has also improved the representation of permafrost dynamics, showing how the ground heat storage retrieved from measurements of subsurface temperature profiles has informed the development of land surface model components for global climate models (Alexeev et al., 2007; Nicolsky et al., 2007; Hermoso de Mendoza et al., 2020; González-Rouco et al., 2021; Steinert et al., 2021). Another approach may be to use the retrieved estimates of continental heat storage as a reference to constraint projections of climate change (Tokarska et al., 2020; Ribes et al., 2021). That is, climate models could be classified depending on how well the models reproduce the change in heat storage in the different components, as it is done with surface temperature increases and other variables (Schmidt et al., 2014; Harrison et al., 2015; Eyring et al., 2019). However, the potential of continental heat storage as a reference may be hampered by the use of models to determine the evolution of heat storage in permafrost soils and inland water bodies, as observations are preferred for evaluating climate simulations.

There are several steps that can be implemented for improving future estimates of ground heat storage. Expanding the number of estimates of ground heat flux has a high priority, as the ground heat storage is the largest term of the continental heat storage. New measurements of subsurface temperature profiles in areas not well represented in the current global database, regions such as northern and central Africa, South America, the Middle East, and southeastern Asia, are important for improving the spatial coverage of the current subsurface temperature dataset. Furthermore, strengthening the global network of subsurface profiles by repeating measurements at previously measured sites would reduce uncertainties for the warming of the continental subsurface in the last decades. Flux estimates from other datasets can be also considered, such as from FluxNet towers and from satellite remote sensing data. Indeed, there is an increasing population of satellites providing information about land surface conditions and changes in land cover, and several methods are also being developed to obtain accurate estimates of climate variables from satellite remote sensing observations in combination with land observational networks and numerical models (Balsamo et al., 2018).

Expanding the permafrost areas considered here, particularly the inclusion of the Tibetan Plateau, would be a priority in the next iterations of this analysis. Further sources of information to retrieve estimates of permafrost heat storage should also be considered in order to increase the confidence of the results obtained here. Ideally, monitoring of liquid water content in permafrost soils along with borehole temperature measurements would form a complementary dataset besides modelling for estimating permafrost heat storage. However, the current observational networks in the Arctic and on the Tibetan Plateau are not equipped to perform such measurements, and their spatial coverage should be expanded to include currently unmeasured zones in the Canadian Arctic and Eurasia (Biskaborn et al., 2015). Monitoring sites tend to be near inhabited locations, existing infrastructure, and resource development sites, leaving large areas without coverage (Smith et al., 2022b). These ground temperature measurements, nevertheless, could be used to inform us about subsurface warming and ground heat storage in future studies. Multimodel simulations using land surface models that represent permafrost, such as those from the sixth phase of the Coupled Model Intercomparison Project (CMIP6), may be considered for including the uncertainty due to different model structures in the analysis. However, direct use of the simulated ice content and soil temperatures from the CMIP simulations is not currently possible because the represented soil column in the models is too shallow to assess the evolution of the thermal state of the ground beyond the near-surface permafrost (Koven et al., 2013; Slater and Lawrence, 2013; Burke et al., 2020; Hermoso de Mendoza et al., 2020; Steinert et al., 2021). Furthermore, these land surface model components do not represent excess ice in the ground or ground subsidence, which bias the represented permafrost thawing (Lee et al., 2014; Rodenhizer et al., 2020). Some ongoing efforts are trying to mitigate this lack of information (e.g. O'Neill et al., 2019; Smith et al., 2022a), which could be incorporated into a future version of this analysis. Replacing ERA-Interim forcing with ERA5 data and forcing for the last decades of the 20th century and the first decades of the 21st century should also be considered.

The inland waters heat storage estimates could be refined using spatially varying morphometry characteristics to determine lake volumes per grid cell. The availability of new datasets like GLOBathy (Khazaei et al., 2022) and new insights from the upcoming Surface Water and Ocean Topography (SWOT) mission would allow such an approach. Using this lake morphology together with an updated lake mask in the global lake model simulations would further improve the lake temperature trends. Such simulations will become available in the upcoming ISIMIP3 round (Golub et al., 2022). In addition, emerging remote sensing products of lake surface temperatures can be used to better calibrate and validate the global lake models, which will further improve the simulated temperature profiles (Golub et al., 2022). Finally, to improve the estimates of heat stored in rivers, better estimates of the water volumes in rivers are required in addition to explicitly modelled river temperatures (Wanders et al., 2019). These will be included in ISIMIP3, as process-based global hydrological models now also simulate river temperatures.

The final goal of this collaboration consists of quantifying continental heat storage at the global scale from observations. Nevertheless, obtaining such an estimate is challenging due to the lack of appropriate observational datasets. Given the amount of time and the resources required to set up observing systems or to expand existing ones, together with the challenges associated with long-term maintenance and data continuity, an intermediate solution based on including more remote sensing and reanalysis datasets in the analysis should be explored in the near term. Relevant variables derived from satellite observations or assimilated in reanalysis products, such as land surface temperature, leaf area index, or snow cover, could drive the modelling frameworks used here, increasing the role of observations in estimates of continental heat storage. Furthermore, the near-global coverage of remote sensing satellite observations and the homogeneity of reanalysis products, together with the relatively long periods included in the datasets, would allow the derivation of estimates useful for climate studies without waiting for years or decades for observational recording.