Contrasting projections of the ENSO-driven CO₂ flux variability in the equatorial Pacific under high-warming scenario

The El Niño–Southern Oscillation (ENSO) widely modulates the global carbon cycle. More specifically, it alters the net uptake of carbon in the tropical ocean. Indeed, over the tropical Pacific less carbon is released by oceans during El Niño, while the opposite is the case for La Niña. Here, the skill of Earth system models (ESMs) from the latest Coupled Model Intercomparison Project (CMIP6) to simulate the observed tropical Pacific CO₂ flux variability in response to ENSO is assessed. The temporal amplitude and spatial extent of CO₂ flux anomalies vary considerably among models, while the surface temperature signals of El Niño and La Niña phases are generally well represented. Under historical conditions followed by the high-warming Shared Socio-economic Pathway (SSP5-8.5) scenarios, about half the ESMs simulate a reversal in ENSO–CO₂ flux relationship. This gradual shift, which occurs as early as the first half of the 21st century, is associated with a high CO₂-induced increase in the Revelle factor that leads to stronger sensitivity of partial pressure of CO₂ (pCO₂) to changes in surface temperature between ENSO phases. At the same time, uptake of anthropogenic CO₂ substantially increases upper-ocean dissolved inorganic carbon (DIC) concentrations (reducing its vertical gradient in the thermocline) and weakens the ENSO-modulated surface DIC variability. The response of the ENSO–CO₂ flux relationship to future climate change is sensitive to the contemporary mean state of the carbonate ion concentration in the tropics. We present an emergent constraint between the simulated contemporary carbonate concentration with the projected cumulated CO₂ fluxes. Models that simulate shifts in the ENSO–CO₂ flux relationship simulate positive bias in surface carbonate concentrations.

1 Introduction

Since the beginning of the industrial era, human activities such as fossil fuel combustion, land-use changes, and cement production have released huge amounts of greenhouse gases (predominantly CO₂), leading to the ongoing planetary-scale climate change. This excess CO₂ in the atmosphere is partly absorbed by the ocean and terrestrial biosphere, buffering the rate of warming (Doney et al., 2014; Le Quéré et al., 2016). Over 2010–2019, approximately 3.4±0.9 and 2.5±0.6 Pg C yr⁻¹ are absorbed by the land and ocean, respectively, with substantial interannual variability (Friedlingstein et al., 2020). Due to its strong feedback on climate, improved understanding of this variability, its governing mechanisms, and how these mechanisms may evolve in the future are required to constrain future climate change projections.

Due to its vast area, the tropical Pacific is the most important CO₂ outgassing region in the world oceans today (Takahashi et al., 2009), representing more than 17 % of the global ocean CO₂ uptake (0.44±0.41 Pg C per year for 1990–2009 and 18^∘ S–18^∘ N; Ishii et al., 2014), and it is projected to be the region with the second highest amount (after the Southern Ocean) of area-integrated anthropogenic carbon uptake in the 21st century under a high CO₂ scenario (Tjiputra et al., 2010; Roy et al., 2011). In terms of interannual variability, the equatorial Pacific CO₂ flux represents the dominant mode of variability of the global oceanic CO₂ flux variations (Wetzel et al., 2005; Resplandy et al., 2015; Landschützer et al., 2016). Some Earth system models (ESMs) also show the CO₂ flux in the Southern Ocean as the dominant mode (Resplandy et al., 2015). In this region, the mechanistic driver is associated with the El Niño–Southern Oscillation (ENSO), which has been well established and thoroughly documented in many previous observational and modelling studies. For instance, Feely et al. (2006) showed strong negative correlation between CO₂ fluxes and ENSO over the equatorial Pacific using observations from 1981 to 2004. Using ocean biogeochemical general circulation models forced with atmospheric reanalysis, similar regional CO₂ flux fluctuations in response to ENSO have been simulated (Winguth et al., 1994; Bousquet et al., 2000; Valsala et al., 2014; Wang et al., 2015).

The biogeochemical processes constraining the CO₂ fluxes in the equatorial Pacific are strongly influenced by the ENSO-induced physical processes. These processes can be formulated as follows: during El Niño events, warmer sea surface temperature reduces the CO₂ solubility, which increases seawater partial pressure of CO₂ (pCO₂, Le Borgne et al., 2002; Patra et al., 2005; Ishii et al., 2014). In parallel, during those events, weaker upwelling of nutrient-rich and dissolved-inorganic-carbon-rich subsurface water acts to reduce the surface seawater pCO₂ (Feely et al., 2006; Long et al., 2013; Wang et al., 2015). The opposite happens during the La Niña phase. Among these competing processes, the ENSO-driven interannual variability of CO₂ flux is presumably dominated by the modulation of dissolved inorganic carbon (DIC) concentrations by the upwelling process (McKinley et al., 2004; Li and Xu, 2013; Jin et al., 2017). Therefore, it is the change in thermocline depth and upwelling strength during the ENSO phase that mainly governs the tropical Pacific CO₂ flux anomalies by constraining surface DIC concentration (e.g. Doney et al., 2009). In addition, CO₂ flux anomaly variability in the tropical Pacific is also related to the poleward Ekman transport driven by the easterly trade winds (Liao et al., 2020).

While models simulating only the ocean are able to simulate the relationship between CO₂ and ENSO (e.g. McKinley et al., 2004; Wetzel et al., 2005; Li and Xu, 2013), this is not always the case for fully coupled Earth system models (ESMs). Indeed, based on ESM simulations from the Coupled Model Intercomparison Project 5 (CMIP5, Taylor et al., 2012), Dong et al. (2017) showed that over the historical period some models underestimate the observed surface DIC variability and consequently the CO₂ flux anomalies. They attributed this to a weak relationship between the simulated upwelling variations and the respective ENSO phases. Jin et al. (2019) showed that some ESMs poorly simulate the spatial pattern of the tropical Pacific CO₂ fluxes in response to ENSO over the historical period. They attributed this to the weak surface DIC-induced CO₂ flux variability during ENSO; e.g. the anomalously low DIC signals associated with ENSO are insufficient to counteract the solubility effects induced by sea surface temperature (SST).

The main focus of this paper is to determine how the ENSO-induced variability of sea–air CO₂ fluxes may be altered in the high-CO₂ future in ESM projections. In this study, the capability of the latest ESM collection from Coupled Model Intercomparison Project 6 (CMIP6) (Eyring et al., 2016) to reproduce the observed ENSO–CO₂ flux relationship over the contemporary period is first evaluated. Next, we analyse how this relationship evolves in future projection run under a high-warming scenario. Given the importance of carbon cycle climate feedback on future projections (e.g. Arora et al., 2020) and the large-scale impact of ENSO on the global climate, such evaluation is timely and necessary. In particular, the aim is to identify and elucidate emerging consistent patterns among the ESMs to better constrain future changes in ENSO-induced variability in the equatorial Pacific. Studying the future evolution of ENSO-related CO₂ flux variations is also crucial because ENSO, the most dominant mode of global climate variability, and its extremes are projected to become more frequent, more intense, and more extended in spatial impact (Cai et al., 2015).

The paper is organized as follows. Section 2 introduces the observational and model datasets, the study area, and the methods used to analyse the relationship between ENSO and sea–air CO₂ fluxes. Results of the contemporary ENSO-related spatial patterns and ENSO–CO₂ flux relationship reversal and variability drivers are presented in Sect. 3, while Sects. 4 and 5 provide the discussion and summary of this study.

2 Data and methodologies

2.1 Observational and CMIP6 datasets

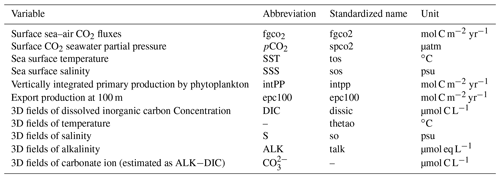
The ocean variables analysed in this study are listed in Table 1. These variables are extracted from different observational and simulation products at monthly temporal resolution. For observation-based fgco₂, the monthly reconstruction values from 1982 to 2015 based on a two-step neural network data interpolation (MPI-SOM-FFN) is used (Landschützer et al., 2016). Gridded monthly SST observations are taken from the Japanese 55-year reanalysis data (JRA-55) from 1958 to 2019 (Kobayashi et al., 2015; Harada et al., 2016). The subsurface temperature profiles over the 1985–2014 period are computed from the ORAS5 reanalyses (Zuo et al., 2019). Total alkalinity average estimates, including measurements between 1972 and 2013, have been retrieved from the GLODAP version 2 data product (Lauvset et al., 2016). Finally, the observed DIC climatology over the 2004–2017 period is extracted from the Keppler et al. (2020) dataset. All variables are given at a regular 1×1^∘ spatial horizontal resolution.

Table 1 Ocean variables used in this study. The full name, the abbreviation, standardized CMIP6 name, and the unit of each variable are all also given.

For the Earth system model simulations, the monthly output fields of surface fgco₂; pCO₂; SST; sea surface salinity (SSS); alkalinity (ALK); integrated primary production (intPP); and 3D temperature, DIC, and alkalinity concentrations are taken from the Coupled Model Intercomparison Project phase 6 (CMIP6, Eyring et al., 2016) database. At the time of study initiation, 16 ESMs provided the variables required for the analysis (see Table 2). The simulation variant for each model is chosen according the availability of the variables shown in Table 1. Given the variety of (irregular) grids among the models, the model datasets are spatially regridded into a regular $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ grid using bilinear interpolation provided by climate data operators (CDOs). The vertical resolutions of 3D temperature and DIC are linearly interpolated at 20 m resolution from the surface down to 1000 m depth.

In this study, analyses are conducted over the same contemporary reference period 1985–2014, the end of the century future period (2071–2100) under the high CO₂ Shared Socio-economic Pathway scenario (SSP5-8.5, O'Neill et al., 2016), and the whole 1850–2100 period, combining both historical and SSP5-8.5 concentration-driven experiments. This high-warming scenario has been chosen in order to use a clear signal with a high signal to noise ratio. Indeed, using a high-emission end member scenario gives us the best chance to actually see a change in the strong relationship between ENSO and CO₂ fluxes. The model simulation outputs are first evaluated against the observations for the reference period, followed by analysis of future evolution and changes with respect to the reference period.

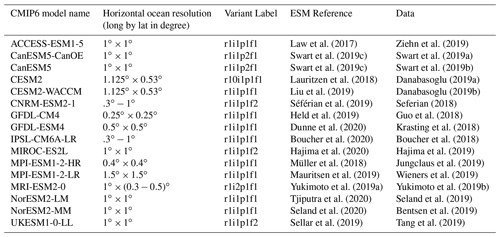
Law et al. (2017)Ziehn et al. (2019)Swart et al. (2019c)Swart et al. (2019a)Swart et al. (2019c)Swart et al. (2019b)Lauritzen et al. (2018)Danabasoglu (2019a)Liu et al. (2019)Danabasoglu (2019b)Séférian et al. (2019)Seferian (2018)Held et al. (2019)Guo et al. (2018)Dunne et al. (2020)Krasting et al. (2018)Boucher et al. (2020)Boucher et al. (2018)Hajima et al. (2020)Hajima et al. (2019)Müller et al. (2018)Jungclaus et al. (2019)Mauritsen et al. (2019)Wieners et al. (2019)Yukimoto et al. (2019a)Yukimoto et al. (2019b)Tjiputra et al. (2020)Seland et al. (2019)Seland et al. (2020)Bentsen et al. (2019)Sellar et al. (2019)Tang et al. (2019)

Table 2 List of the 16 CMIP6 models used in this study with the horizontal resolution of the ocean component, variant label, model, and data references all given. Note that most of the models have irregular grids and the resolutions quoted in the table are approximate.

2.2 Variable anomalies, Niño34 index, and thermocline depth computation

The analysis focuses on the correlation between CO₂ flux anomalies and Niño34 index. First, the monthly anomalies of sea–air CO₂ fluxes at each grid point are computed by detrending each calendar month separately using a cubic smoothing spline (implemented by the function smooth.spline in R software; R Core Team, 2016) over the period 1850–2100. For instance, the non-linear trend for January at a given grid point is removed from the respective time series comprising all January values. The SST and pCO₂ anomalies used in the analyses are also computed in the same manner. The degree of freedom of the spline is set to get a good compromise between the smoothness (smoothing parameter above 0.8) and the number of parameters (knots) of the spline used to estimate the trend over to whole equatorial Pacific (Hastie and Tibshirani, 1990, chap. 10). The degree of freedom is set to 5 for SST and fgco₂. A degree of freedom of 12 is needed for pCO₂ given its steeper increase.

The Niño34 index corresponds to the standardized area-weighted mean SST anomalies over the Niño34 region: 5^∘ S–5^∘ N, 190^∘ E–240^∘ E. These anomalies are computed relative to the 1981–2010 climatology. For the CMIP6 model outputs, the SST values are first detrended over the 1850–2100 period using a cubic spline. Following this, a model-specific Niño34 index is computed relative to the 1981–2010 climatology. Hereafter, the regimes referred to as El Niño (or La Niña) are defined from the respective Niño34 indices (specific for observations and each model). Months with a Niño34 index above 1 standard deviation (SD) of each dataset are categorized as El Niño regimes; those that are below −1 SD are classified as La Niña regimes.

The thermocline is a transition layer where the temperature decreases rapidly with depth from the warm surface mixed layer to the cold deep-water layer, where the temperature is relatively uniform. A deeper thermocline (e.g. during El Niño) limits the amount of interior DIC brought to shallower depths by upwelling. This indicator is used in this study to assess the changes in the mechanisms linking ENSO and CO₂ fluxes in the present day and in the future projections. The thermocline depth is typically defined as the depth with the maximum vertical temperature gradient (Zhu et al., 2021, and references therein). In this paper, the gradient is computed every month as the vertical difference within each 20 m layer (after the vertical interpolation), and the thermocline depth is the average depth of the layer with the highest gradient.

2.3 Thermal and non-thermal contributions to surface pCO₂

In order to differentiate the thermal (th, driven by SST) and non-thermal (nt, driven by other factors, such as DIC, alkalinity, and salinity) contributions, the temporal variations of surface ocean pCO₂ is decomposed into the two terms following Takahashi et al. (1993, 2002). Seawater pCO₂ is thermodynamically dependent on temperature and is computed from the temperature sensitivity of CO₂ γ_T (4.23 % ^∘C⁻¹). This sensitivity has experimentally been determined and is associated with very little error (Takahashi et al., 1993), which is not further considered. The thermal pCO₂ component $p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{th}}$ is computed as follows:

$$\begin{array}{}\text{(1)}& p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{th}}=<p{\mathrm{CO}}_{\mathrm{2}}{>}_{\mathrm{annual}}\exp \left({\mathit{\gamma }}_T(\mathrm{dSST}-<\mathrm{dSST}>)\right).\end{array}$$

In Eq. (1), the annual pCO₂ average, $<p{\mathrm{CO}}_{\mathrm{2}}{>}_{\mathrm{annual}}$, is perturbed with temperature anomalies computed as the difference between the detrended SST, dSST (done with a cubic spline), and the long-term mean dSST, $<\mathrm{dSST}>$. The non-thermal component ($p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{nt}}$), which reflects the effect of biophysical processes, is computed by normalizing the pCO₂ to $<\mathrm{dSST}>$ (Takahashi et al., 2002):

$$\begin{array}{}\text{(2)}& p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{nt}}=p{\mathrm{CO}}_{\mathrm{2}}\exp \left({\mathit{\gamma }}_T(<\mathrm{dSST}>-\mathrm{dSST})\right).\end{array}$$

In Eq. (2), the exponential term removes the SST-associated pCO₂ variation. This decomposition is well known and extensively used at regional and global scale (e.g. Landschützer et al., 2018; Jiménez-López et al., 2019; Ko et al., 2021).

2.4 Biological contribution to surface pCO₂

The buffering capacity of the ocean is a measure of the ability of the ocean to take up carbon and is quantified by the Revelle factor, $R=\frac{\mathrm{\Delta }p{\mathrm{CO}}_{\mathrm{2}}}{p{\mathrm{CO}}_{\mathrm{2}}}/\frac{\mathrm{\Delta }\mathrm{DIC}}{\mathrm{DIC}}$ (Revelle and Suess, 1957). The Revelle factor R is the ratio of the relative change of seawater pCO₂ (or aqueous CO₂ concentration, CO_2(aq)) to the relative change of dissolved inorganic carbon ($\mathrm{DIC}={\mathrm{CO}}_{\mathrm{2}\left(\mathrm{aq}\right)}+{\mathrm{HCO}}_{\mathrm{3}}^{-}+{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$, Egleston et al., 2010; Hauck and Völker, 2015). The sensitivity of pCO₂ to DIC perturbations can be estimated using the buffer factor γ_DIC that is related to the Revelle factor as ${\mathit{\gamma }}_{\mathrm{DIC}}=\frac{\mathrm{DIC}}{R}$ and can be explicitly retrieved from the carbonate system parameters (Egleston et al., 2010). To summarize, the higher the Revelle factor, the lower the buffer capacity (or the buffer factor γ_DIC) of the ocean and its CO₂ uptake capacity. The annual evolution of surface Revelle factor and buffer factor γ_DIC for CMIP6 models over the 1850–2100 period in the equatorial Pacific (defined below) are given in Fig. 1. Using this relationship, the reduction in pCO₂ can be quantified as a result of reduction in DIC concentration, e.g. associated with biological carbon absorption:

$$\begin{array}{}\text{(3)}& \mathrm{\Delta }p{\mathrm{CO}}_{\mathrm{2}}{}_{\mathrm{bio}}={\displaystyle \frac{\mathrm{\Delta }{\mathrm{DIC}}_{\mathrm{bio}}}{{\mathit{\gamma }}_{\mathrm{DIC}}}}p{\mathrm{CO}}_{\mathrm{2}},\end{array}$$

where ΔDIC_bio is the mean reduction in surface DIC concentration due to biological production (estimated from the monthly intPP in [mol C m⁻² per month] divided by the euphotic layer depth, here assumed to be 100 m). A similar approach has been used in Hauck and Völker (2015) to determine the impact of biological activity on surface pCO₂ in the Southern Ocean. The ΔpCO_2bio is relevant to evaluate the biological contributions during El Niño and La Niña to pCO₂ variations. This quantity non-linearly increases with ΔDIC_bio; i.e. biological contributions to pCO₂ variations increase as the buffering capacity decreases.

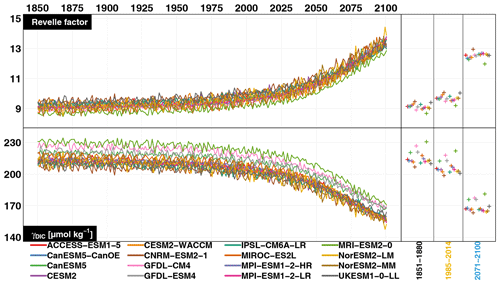
Figure 1 Annual Revelle factor and γ_DIC (in µmol kg⁻¹) for CMIP6 models. Average Revelle factor for each ESM over the early historical (1851–1880), contemporary (1985–2014), and future (2071–2100) periods are given on the right-hand side of the figure..

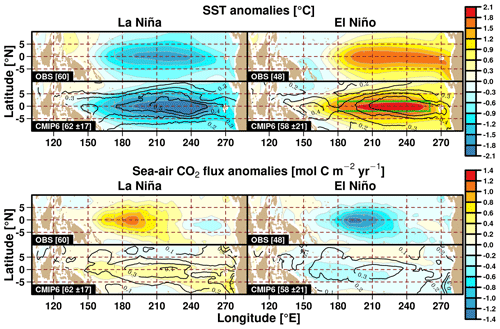
Figure 2 Observed JRA-55 and mean CMIP6 SST (in ^∘C, top) and observed MPI-SOM-FFN and mean CMIP6 sea–air CO₂ fluxes (in mol C m⁻² yr⁻¹, bottom), shown as average anomalies over the 1985–2014 contemporary period for the La Niña (left) and El Niño (right) regimes. The number of months in each regime for the observations and the mean number with 1 standard deviation for the CMIP6 ensemble are both given in square brackets. Black contours represent the CMIP6 inter-model ensemble anomaly standard deviation during each ENSO phase. The green box in the lower-right SST panel illustrates the EP (equatorial Pacific) area.

2.5 Study area

For analysis of integrated surface properties, the focus on evaluating the anomalies over the equatorial Pacific is given within the 2^∘ S–2^∘ N and 180^∘ E–260^∘ E domain (hereafter referred to as the equatorial Pacific or simply EP). The EP area is indicated by the green box in the bottom-right SST panel of Fig. 2. This region is identified as the common domain where the models and observation show the largest change in SST between ENSO phases. The same domain is also considered for subsurface analysis conducted in this study, namely the changes in the vertical DIC, carbonate ion concentration, and temperature profiles between the contemporary and future periods.

3 Results

3.1 Contemporary (1985–2014) ENSO-related patterns

Figure 2 depicts the average tropical Pacific SST and sea–air CO₂ flux anomalies for La Niña and El Niño regimes over the contemporary period from observations and the CMIP6 multi-model mean. The corresponding values for each model are given in Figs. S1 and S2 in the Supplement. For surface temperature anomalies, some models clearly simulate too strong and too broad SST anomalies (Fig. S1), but the CMIP6 multi-model ensemble mean values show a strong resemblance with the observations, albeit with slightly too strong anomalies in the central equatorial Pacific. However, the warm anomalies observed over the coast of Peru during El Niño are slightly weaker in the model simulations. In these two regions, the inter-model variability is also large (contour lines in Fig. 2). For the sea–air CO₂ flux anomalies, the simulated spatial extent are less in agreement with the observational estimates. The spatial distribution of CO₂ flux anomalies is also different from one model to another, and none of the models simulate a spatial correlation with observations of more than 0.8 according the regime, with negative correlation even present (see Fig. S3 in the Supplement). The co-location of spatial distribution of the temperature and CO₂ flux anomalies during the ENSO phase is quite straightforward in the observations while it seems less obvious in the models. This suggests that some of the observed mechanisms governing the ENSO-related variability of CO₂ flux are not well reproduced by the models. Most models simulate weaker CO₂ flux anomalies compared to the observations, which is consistent with the CMIP5 model results (Dong et al., 2017). Nevertheless, the multi-model mean reproduces the observed outgassing anomaly signals over most of the tropical Pacific during La Niña (and vice versa for El Niño). The same results are obtained when looking for more extreme El Niño and La Niña regimes (for months with a Niño34 index above 1.5 and below −1.5 SD, respectively, not shown).

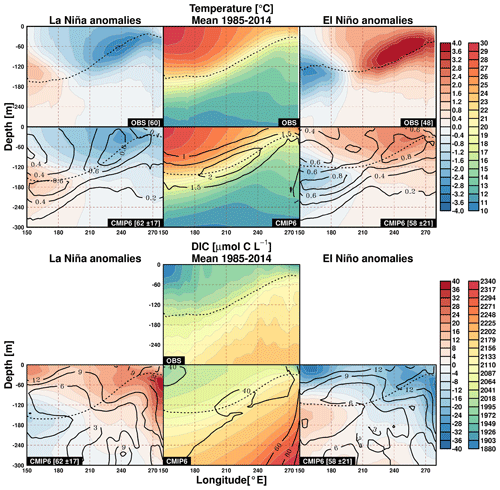
Figure 3 Observed and mean CMIP6 vertical sections of temperature (in ^∘C, top) and DIC (in µmol C L⁻¹, bottom) as a zonal (between 2^∘ N and 2^∘ S) average over the 1985–2014 contemporary period (middle column). The average anomalies (differences) relative to contemporary mean are given for the La Niña (left) and El Niño (right) regimes. Note that the observed DIC average represents the climatology over the 2004–2017 period. Dotted lines indicate the average thermocline depth. In square brackets, the number of months in each regime is given for the observations and the mean number (with 1 SD) is given for the CMIP6 ensemble. Black contours represent the standard deviation of the CMIP6 inter-model ensemble anomalies during each ENSO phase.

Figure 3 shows the zonal average of temperature and DIC vertical sections over the contemporary period and its anomalies during the La Niña and El Niño regimes from the observations and the CMIP6 ensemble mean (for DIC, only the mean values is shown for observations). During El Niño events, the observations depict a clear warming signal in the eastern part of the tropical Pacific extending throughout the upper ocean with a maximum warming around 70 m depth. A cool anomaly can be seen in the western part of the domain at approximately 150 m depth. The opposite anomaly patterns can be seen during La Niña. The observed and simulated long-term mean temperature patterns are quite similar, whereas the magnitude of the anomalies is weaker in the CMIP6 multi-model mean. The contemporary DIC average concentration is generally higher in the models than in the observations. Note that the observed average is the result of the climatology over the 2004–2017 period, whereas the average for CMIP6 is computed over 30 years (1985–2014). The subsurface DIC signals of anomalies contrasting La Niña and El Niño regimes are pronounced in the upper layer and to the east of 240^∘ E down to 300 m, with positive (negative) anomalies during La Niña and El Niño associated with changes in the upwelling dynamics. This area also presents the largest inter-model variability. Consequently, this DIC anomaly determines the CO₂ flux anomaly at the surface. An opposite DIC anomaly signal is simulated in the western part of the section below 100 m depth. The zonal average of temperature and DIC along the vertical sections and their anomalies in each individual model are given in Figs. S4 and S5 in the Supplement.

3.2 Transient changes in ENSO–CO₂ flux relationship

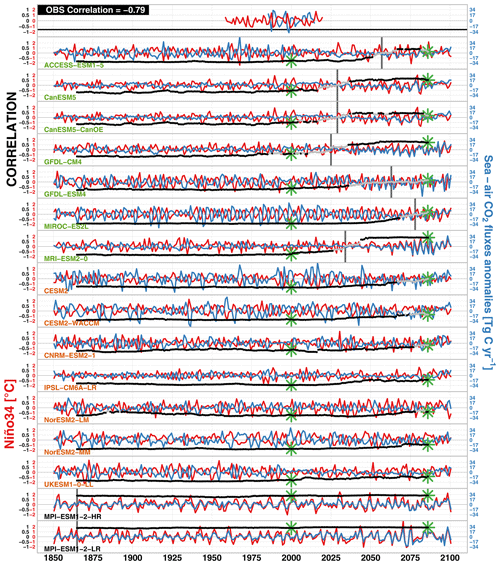
Figure 4 CMIP6 model ensemble annual time series of the Niño34 index (in ^∘C, red lines), the average CO₂ flux anomalies over the EP area (in Tg C yr⁻¹, blue lines), and the correlation for each 30-year moving window (significant correlations are indicated by black dots, and the non-significant ones are shown in grey). The vertical bars indicate the centre 30-year period with the first positive correlation. The first row shows the observed time series of the Niño34 index and average CO₂ fluxes anomalies over the 1985–2014. The green asterisks indicate the correlation of the models over the observed and 2071–2100 periods. Model names are given in green for the models with a shifting correlation sign, those maintaining the negative correlation are shown in orange, and those simulating positive correlation already in 1850 are shown in black.

In this section, the characteristics of sea–air CO₂ flux variability associated with ENSO are investigated over the EP area. Figure 4 represents the annual Niño34 index and the annual average CO₂ flux anomalies from observations and 16 CMIP6 models. A correlation analysis between CO₂ flux anomaly and ENSO index is performed to study the strength and direction of the linear relationship between these two variables. The statistical significance of these correlations is assessed by testing if the correlation follows a Student's t distribution (with N-2 degrees of freedom, N being the number of years) at the 95 % significance level. The correlation between the annual CO₂ flux anomaly and annual ENSO index is given for the models for each 30-year sliding window (30 years is a typical climatological window used in numerous studies) over the 1850–2100 period. The observed correlation over 1985–2014 is significantly negative ($r=-\mathrm{0.79}$), which is also the case for all the models at the beginning of the 1850–2100 period (except for the two MPI models). Among these models, seven maintain a negative correlation throughout the future period, while seven display a shift toward a positive correlation that occurs as early as 2025. The CMIP6 model correlations over the observational period and the 2071–2100 period are indicated by the green asterisks in Fig. 4 and reported in Table 3. Figure S9 in the Supplement is the same as Fig. 4 but zoomed over the contemporary period.

Table 3 Standard deviations of sea–air CO₂ fluxes (${\mathit{\sigma }}_{{\mathrm{CO}}_{\mathrm{2}}}$); in Tg C m⁻² yr⁻¹) and the Niño34 index (σ_Niño34); in ^∘C and their annual correlation coefficients ρ over the 1985–2014 period. In brackets are the standard deviation and correlation over the 2071–2100 period. The average Revelle factors for each model and both periods are also given. Models in bold have significant correlation for both periods and are the ones selected for the “reversed” and “preserved” groups.

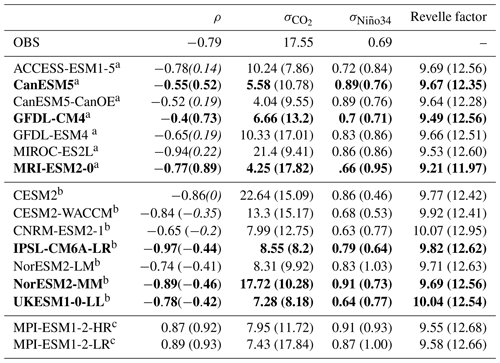
^a The models with shifting towards a positive correlation. ^b The models maintaining negative correlation. ^c The models starting with positive correlation. Non-significant correlations are given in italic.

Figure 4 also shows that the amplitude of CO₂ flux anomalies and their covariance with the Niño34 index are not uniform across the models. The correlation between sea–air CO₂ flux anomalies and Niño34 are given in Table 3 along with their respective standard deviations ${\mathit{\sigma }}_{{\mathrm{CO}}_{\mathrm{2}}}$ and ${\mathit{\sigma }}_{\mathrm{Ni}\stackrel{\mathrm{̃}}{\mathrm{n}}\mathrm{o}\mathrm{34}}$. The contemporary variability of CO₂ flux anomaly is underestimated by most of the models (see Table 3) and increases or decreases in the future according the models. Six models, given in bold in Table 3, are selected to illustrate the shifting and non-shifting CO₂ flux anomaly responses to ENSO variability in their future projections. These are the models that are selected because they best reproduce the observed Niño index and CO₂ flux anomaly correlations in the contemporary period while the correlation is significant over contemporary and future periods.

The monthly Niño34 index of the six selected models is presented against the CO₂ fluxes anomalies in Fig. 5 for both the contemporary (1985–2014) and future (2071–2100) periods. Values from present-day observations are also depicted. The models in the first row (CanESM5, GFDL-CM4, MRI-ESM2-0) show a change in the Niño34-CO₂ flux correlation, while the models in the second row (IPSL-CM6A-LR, NorESM2-MM, UKESM1-0-LL) maintain the sign of the correlation between 1850 and 2100. This reversal is thus independent of the model's ability to reproduce the observed correlation over the contemporary period, though the models in the first row tend to simulate lower than observed CO₂ flux anomaly variability. Hereafter, these first row models that simulate a reversal in ENSO–CO₂ flux relationship are referred to as “reversed” ESMs, while the other three ESMs that maintain the contemporary relationship are referred to as “preserved” ESMs. These two groups of models are confronted in further analysis.

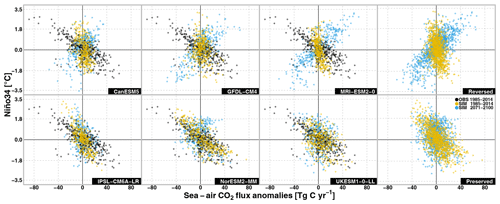
Figure 5 Scatter plots for the six selected models of the monthly Niño34 index (in ^∘C) against the monthly CO₂ flux anomalies (in Tg C yr⁻¹) averaged over the EP domain in the 1985–2014 contemporary period (in yellow) and the 2071–2100 period (in blue). The observed scatter plot is given in black. The top panels show CanESM5, GFDL-CM4, MRI-ESM2-0, and all reversed ESMs. The bottom panels are for IPSL-CM6A-LR, NorESM2-MM, UKESM1-0-LL, and all preserved ESMs.

3.3 Drivers of ENSO–CO₂ flux variability

In order to elucidate the drivers of the modified relationship in the reversed ESMs, the thermal and non-thermal contributions to pCO₂ are investigated. Figure 6 represents the average El Niño and La Niña of the pCO₂ anomaly means for the reversed and preserved ESMs over the early historical (1851–1880), contemporary, and future periods. As expected, the pCO₂ thermal (non-thermal) component always induces positive (negative) anomalies during El Niño, while the opposite is true during La Niña. The non-thermal component is rather dominant (non-thermal/thermal ratios >100 %) during the early historical period (1851–1880) and even more dominant during La Niña (bigger ratios). This explains the total pCO₂ positive anomalies during La Niña (consistent with enhanced CO₂ outgassing; Fig. 2) and the negative anomalies during El Niño (consistent with weakened CO₂ outgassing) for both groups of ESMs over the early historical and contemporary periods. Over the future period, the dominance of the non-thermal component is even enhanced for preserved ESMs, which maintain the same CO₂ flux–ENSO relationship. However, for the reversed ESMs the thermal component becomes dominant by the end of the 21st century (ratio <100 %), inducing total pCO₂ negative anomalies during La Niña and positive anomalies during El Niño. The dominance of the thermal component explains the reversal in the ENSO–CO₂ flux relationship highlighted in Figs. 4 and 5.

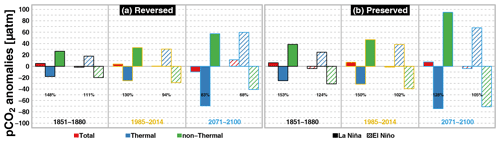
Figure 6 El Niño and La Niña average of total (in red), thermal (in blue), and non-thermal (in green) pCO₂ mean anomalies (in µatm) for the reversed (a) and preserved (b) ESMs over the early historical (1851–1880), contemporary (1985–2014), and future (2071–2100) periods in the EP domain. The absolute ratio between the non-thermal and thermal components is given (in %) for each period, group, and ENSO phase.

In a high CO₂ future, it is expected that the pCO₂ will be more sensitive to SST and surface DIC modulations due to lower buffering capacity (Fig. 1; see also Gallego et al., 2020). It is therefore useful to determine whether or not the reversal in the ENSO–pCO₂ response can solely be attributed to the background atmospheric CO₂ increase. Indeed, the non-thermal component is already dominant and will become more dominant as CO₂ rises. In order to test this hypothesis, the anomaly estimates of the thermal and non-thermal components of early historical ENSO pCO₂ signals are scaled to higher background pCO₂, namely the contemporary and future periods. This enables us to evaluate how the non-thermal/thermal ratio varies into the future assuming no change in the biological and physical forcing (i.e. amplitude of ENSO-induced changes in SST and DIC are unchanged). This is done by keeping the dSST variable in Eqs. (1) and (2) at the values of the early historical period, while scaling up the pCO₂ elements to contemporary and future values. A similar figure to Fig. 6 showing these scaled components is given in Fig. S7 in the Supplement. Following this scaling, the non-thermal component remains dominant for the three periods in both groups of models. This means that the pCO₂ increase alone cannot explain the reversal behaviour in the reversed ESMs. It suggests changes in biological and physical forcing are also responsible for the thermal component becoming more dominant in this group of ESMs.

In addition to surface ocean pCO₂, CO₂ flux is estimated using atmospheric pCO₂ and wind solubility coefficient k⋅K₀ as follows:

$$\begin{array}{}\text{(4)}& \mathrm{fgco}\mathrm{2}=k\cdot K_{\mathrm{0}}\cdot (p{\mathrm{CO}}_{\mathrm{2}o}-p{\mathrm{CO}}_{\mathrm{2}a}),\end{array}$$

where k represents the gas transfer velocity and K₀ the solubility coefficient (cf. Wanninkhof, 2014). The anomalies of surface wind and product of k⋅K₀ for each period, group of models and ENSO phase are depicted in Fig. S8 in the Supplement. The amplitude of both anomalies between ENSO phases is larger for the preserved models than the reversed ones, which partly explains the higher amplitude of CO₂ flux variability variation between ENSO phases for the preserved models than the reversed models (see Table 3 and Fig. 5). However, for the respective groups the amplitudes between ENSO phases do not change between given the analysed periods. This means that the wind variability can only have a marginal contribution to CO₂ flux variability and cannot explain the behaviour of the reversed models. In addition, we also note that the relatively low contemporary CO₂ flux variation in the reversed models is also partly attributed to the simulated high alkalinity bias in these models (see Supplement Fig. S9), as high background alkalinity would dampen the DIC-induced pCO₂ variability during the different ENSO phases.

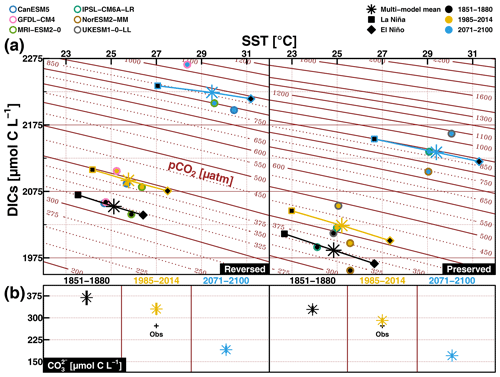
Figure 7 Mean SST (in ^∘C) versus mean salinity-normalized DIC (DICs, in µmol C L⁻¹) over the early historical (1851–1880), contemporary (1985–2014), and future (2071–2100) periods in the EP domain simulated by all reversed and preserved ESMs (a, circle markers). The multi-model mean values of SST and DICs (asterisk markers) from each ESM group, together with their respective mean values during La Niña (square markers) and El Niño (diamond markers), are also depicted for the three periods. Isolevels of pCO₂ for varying SST and DICs are given in the background. Panel (b) shows the multi-model range and mean of surface carbonate concentration (in µmol C L⁻¹) for both groups and three periods.

Next, we quantify the pCO₂ sensitivity to ENSO-induced temperature and DIC changes across different time periods. Figure 7 shows the mean states of SST against surface DICs (salinity-normalized DIC; DICs=DIC$\times \frac{SS{S}_{\mathrm{0}}}{SSS}$, with SSS₀ representing the 30-year surface salinity average in a given period) for reversed and preserved ESMs over the early historical, contemporary, and future periods. The pCO₂ isolevels for varying SST and DIC are computed using the carbonate system parameter codes from the R-package “seacarb” (Gattuso et al., 2020). These values have been computed using ALKs (salinity-normalized surface alkalinity) and SSS from multi-model mean state (over the 1850–2100 period) from reversed and preserved groups separately. The average has been taken over the whole simulation period and shows the small changes in ALKs and SSS from the early historical period to the future period (see Fig. S10 in the Supplement). The multi-model range and mean of average surface carbonate ion concentration is also given for both groups over the three periods.

All models show higher sensitivity of pCO₂ to temperature and DICs perturbations in the future; i.e. the same variations of DIC or temperature in the future will induce a stronger change in surface pCO₂. Indeed, pCO₂ isolevels are getting closer as SST and DICs increase (see Fig. 7). The main difference between the two groups is that the reversed models simulate (i) a higher surface DICs increase from the early historical or contemporary period to the future period and (ii) a lower range of DICs changes during ENSO phases (from the early historical period to the future period, the absolute change of surface DICs between both ENSO phases evolves from 30.26 to 19.45 µmol C L⁻¹ for reversed models and from 44.87 to 34.00 µmol C L⁻¹ for preserved ones). The pCO₂ level and its increase across different time periods are both very similar between the two ESM groups. The simulated temperature changes are also similar between both groups. The higher surface DIC increase in the reversed models can be explained by the higher CO${}_{\mathrm{3}}^{\mathrm{2}-}$ ion concentration at the beginning of the transient simulation, which translates to higher carbon buffer capacity and allows these models to take up more excess carbon from the atmosphere. The lower surface DIC range (between in La Niña and El Niño regimes) in the reversed models could be associated with changes in biology- and/or upwelling-induced surface DIC fluctuations.

Takahashi et al. (1993) also mention pCO₂ sensitivity to alkalinity and salinity. A similar figure as Fig. 7 but for the mean states of SSS against ALKs is given in supplementary Fig. S10. Given the important increase in temperature and DIC from the early historical to the future period (cf. Fig. 7) one panel per model group and period is produced. This figure shows higher SSS and ALKs for reversed models than the preserved ones. For both groups, the ALKs and SSS changes are very small from one period to another, indicating a limited sensitivity of pCO₂ to future changes in salinity and alkalinity. Besides, the amplitude between ENSO phases is small for salinity and alkalinity (<.2 psu for SSS and <6.5 µmol eq L⁻¹ for ALKs). Therefore, the relative contribution of ENSO-induced salinity and alkalinity changes to pCO₂ is smaller than temperature and DIC changes.

Even without climate change, the influence of biological production on perturbing surface pCO₂ is expected to increase with a higher Revelle factor in the future. Here, we quantify the contribution of biological production in reducing the surface pCO₂ (i.e. ΔpCO_{2 bio}) during both La Niña and El Niño phases according to Eq. (3). In the contemporary period, stronger primary productivity during La Niña attenuates the upwelling-induced pCO₂ increase (and vice versa during El Niño). In addition, this anomaly pattern observed in the contemporary period is maintained into the future (see Fig. S12 in the Supplement depicting time series of the average intPP computed over the EP area). Figure 8 shows that these biological contributions significantly increase in the future, while higher ΔpCO_{2 bio} persists during the La Niña phase. This stronger contrast in the biologically induced ΔpCO_{2 bio} difference between La Niña and El Niño regimes is also enhanced by the increased future primary production variability simulated in the respective ESMs (Fig. S12). The projected variability in primary production between La Niña and El Niño is even bigger for the reversed ESMs than for preserved ESMs (i.e. larger by up to a factor of 5; see Fig. S12). Note that the majority of the chosen ESMs simulate a declining trend in the primary production toward the end of the 21st century. The export production at 100 m also shows similar ENSO-induced variability and evolution to the intPP (not shown).

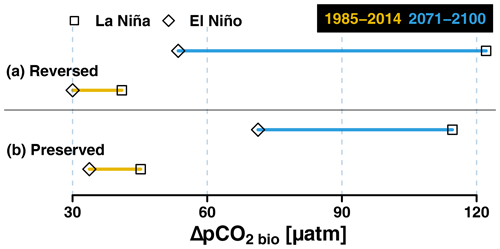
Figure 8 Multi-model mean average biological contribution to the oceanic pCO₂ (in µatm) deficit during La Niña and El Niño regimes for the 1985–2014 and 2071–2100 period for all reversed (a) and preserved (b) models in the EP domain.

As stated above, the primary reason for the enhanced biological contribution of ΔpCO_{2 bio} is driven by the increasing Revelle factor with higher atmospheric CO₂ concentrations in the future (see Fig. 1 and Hauck and Völker, 2015). Assuming that the upwelling-induced DIC variation stays constant in the reversed ESMs, an enhanced primary production fluctuation (higher during La Niña, lower during El Niño) in the future would decrease the ratio between non-thermal and thermal pCO₂ components and could therefore contribute to the simulated reversed relationship (Fig. 6). Fig. S12 also shows that the preserved ESMs also simulate enhanced primary production variability but with a lesser magnitude than the reversed ESMs. However, the contemporary ENSO–CO₂ flux relationships in this ESM group are maintained in the future, suggesting that biological contribution is too low or that other additional processes are at play.

In addition to surface biological activities, the reduction of the non-thermal contribution to the total pCO₂ in the reversed ESMs can also be attributed to changes in upwelling-induced surface DIC modulation. Here, we examine the mean vertical profiles of DIC and temperature and carbonate ion in the EP domain across the two ESM groups. Figure 9 shows the average vertical profiles of DIC and temperature for the two groups of ESMs over the EP domain from the surface down to 300 m depth. Both groups consistently show DIC and temperature increase in the future, but the change varies in magnitude and vertical distribution.

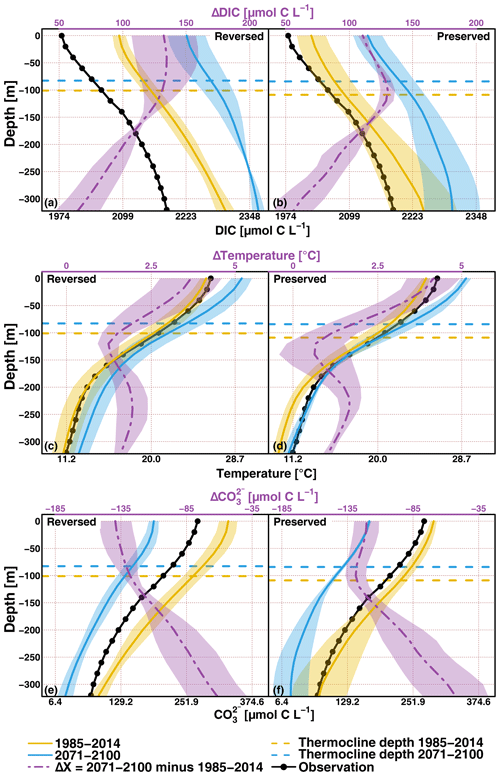
Figure 9 Multi-model mean of vertical DIC (in µmol C L⁻¹, a and b), temperature (in ^∘C, c and d), and carbonate ion concentration (in µmol C L⁻¹, e and f) profiles over the 1985–2014 (in yellow lines) and 2071–2100 (in blue lines) periods for reversed (a, c, e) and preserved (b, d, f) models. The profile difference between both period profiles (Δ) is given as purple dashed–dotted lines. The black lines with dots are the observed profile for the three variables. The dashed horizontal lines indicate the average thermocline depth for each groups and time periods. A value of 1 standard deviation is given in shaded colours.

Indeed, the vertical DIC gradient is a key factor driving ENSO-related CO₂ flux variability throughout the vertical column. The reversed ESMs simulate higher historical DIC (yellow lines in the first row of Fig. 9) making them more biased than the preserved ones, but both groups have a similar vertical profile. Bias in the interior DIC may be associated with the simulated mean alkalinity state (Figs. S9 and S11 in the Supplement), which is likely associated with variation in particulate inorganic carbon formulation in ESMs. The simulated future DIC increase is similar at 100 m and deeper for both groups (dashed purple lines). However, the increase from the surface to 100 m is larger for the reversed ESMs. This leads to a stronger reduction in vertical DIC gradient, which would also contribute to less ENSO-induced surface DIC variability in the reversed ESMs. This is also consistent with the projected more dominant thermal contribution relative to the total pCO₂. The future increase in the upper-ocean DIC concentration is associated with the uptake of anthropogenic carbon from the atmosphere. We note that the increase in DIC concentration at depth can also be associated with the shallow water overturning circulation, which advects southern DIC-rich (and carbonate-poor) waters into the region (Toyama et al., 2017; Rodgers et al., 2020) and can also affect the buffering capacity of upwelled water mass.

The higher surface DIC increase is also illustrated in the right panel of Fig. 10, depicting that the reversed ESMs simulate more carbon uptake (or less cumulated DIC loss because the tropical Pacific is a mean outgassing system) than the preserved models over the transient simulation period. This is attributed to the higher surface and subsurface alkalinity and CO${}_{\mathrm{3}}^{\mathrm{2}-}$ (see Figs. S10 and S11 for ALK and the bottom row of Fig. 9 and the left panel of Fig. 10 for CO${}_{\mathrm{3}}^{\mathrm{2}-}$) concentration simulated by the reversed ESMs at the beginning of the transient simulation from the surface to 300 m depth. The considerably higher alkalinity (and carbonate ion) concentration in the reversed models yield a water mass with higher buffer capacity, which allows them to uptake more atmospheric carbon in the future. This is the first-order explanation for the projected higher surface CO${}_{\mathrm{3}}^{\mathrm{2}-}$ reduction (see the bottom row of Fig. 9 and the left panel of Fig. 10). This higher buffer capacity also dampens the DIC-induced pCO₂ variability during ENSO phases, which partly explains the smaller magnitude of CO₂ flux variability in the reversed models that was previously mentioned.

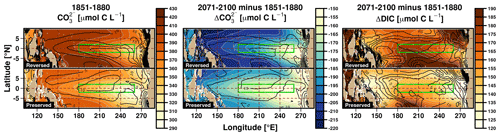
Figure 10 Maps of average surface CO${}_{\mathrm{3}}^{\mathrm{2}-}$ concentration (µmol C L⁻¹) for the reversed and preserved ESMs for the 1851–1880 period are given in the left panel. The middle panel shows the carbonate ion concentration difference between the 2071–2100 and 1851–1880 periods. The right panel shows the surface DIC concentration difference between the 2071–2100 and 1851–1880 periods. The green boxes outline the EP region.

The relationship between historical surface carbonate concentration and CO₂ uptake can be generalized for all models, providing a new emergent constraint. Figure 11 shows contemporary surface carbonate concentrations against the cumulated sea–air CO₂ flux over the 1985–2014 and 1850–2100 periods over the EP for all the models except the MPI models. Correlation at 0.65 and 0.67 indicates that the carbonate concentration is a good indicator of the buffering capacity of the model: the higher the carbonate, the lower the cumulated CO₂ outgassing (i.e. more carbon uptakes). The preserved ESMs are less biased in terms of carbonate concentration and cumulated CO₂ flux over the contemporary period, which tends to indicate that their behaviour should be more reliable.

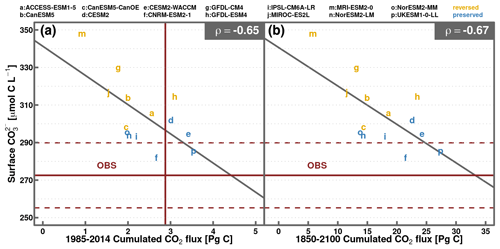
Figure 11 Average contemporary surface CO${}_{\mathrm{3}}^{\mathrm{2}-}$ concentration (in µmol C L⁻¹) plotted against the cumulated sea–air CO₂ fluxes (in Pg C) in the EP region from 1985 to 2014 (a) and 1850 to 2100 (b). ρ is the correlation, and reversed ESMs are marked in yellow, while preserved ESMs are marked in blue. The observations are given as brown lines, with dashed lines being the carbonate observation error.

The preserved ESMs simulate stronger warming at the surface (see the middle row of Fig. 9), suggesting stronger future stratification, which is consistent with the higher increase in the subsurface DIC (e.g. associated with the biological remineralization) with less upwelling. Consequently, the weaker future stratification in the reversed ESMs is also consistent with the more uniform DIC vertical profile.

ENSO-induced upwelling variability alters the surface DIC anomalies. Figure S13 in the Supplement depicts time series of the average stratification index (SI) computed over the EP domain (see the Supplement for the definition and formulation). There is no significant difference in the SI evolution between the reversed and preserved ESM groups. The SI is expected to increase toward the end of the 21st century, consistent with future warmer upper layer and weaker upwelling. In all ESMs, the stratification variation due to ENSO, i.e. higher stratification during El Niño events (indicating weaker upwelling state) and vice versa during La Niña, is maintained in the future. Despite increasing future stratification and shallowing of thermocline depth (see Fig. 9), the ENSO-driven surface DIC variation in all ESMs (anomalously lower DIC during El Niño and higher DIC during La Niña) is also maintained in the future (see Fig. S14).

4 Discussion, limitations and perspectives

In the tropical Pacific, the dominant mode of sea–air CO₂ flux variability over the interannual timescale has been established to be associated with ENSO. Here, by evaluating the capacity of 16 CMIP6 ESMs to reproduce this relationship over the historical period provides a valuable means to validate their performance. As shown in Table 3, while most ESMs are able to reproduce the observed contemporary relationships (i.e. negative correlation or outgassing anomaly during La Niña and vice versa during El Niño), there are two ESMs that simulate the complete opposite relationship. Furthermore, the amplitude of the Niño34 (CO₂ flux) variability also varies considerably among models over the contemporary period, from 0.91 (0.23) to 1.32 (1.29) times, as compared to the observations (Table 3). As with the previous generation of ESMs (Jin et al., 2019), considerable differences in the spatial extent of CO₂ flux anomaly patterns associated with ENSO variability are also simulated in the current CMIP6 ESMs.

Model projections suggest an enhanced ENSO variability in the future associated with the intensification of upper-ocean stratification (Cai et al., 2018). Due to the climate–carbon cycle feedback, analysing how the ENSO-induced CO₂ fluxes will be altered by future climate change could provide a valuable insight into the projections of long-term anthropogenic climate change (Betts et al., 2020). Among the analysed ESMs, half of models show a reversal in their ENSO–CO₂ flux relationship in the equatorial Pacific (i.e. from an anomalous CO₂ uptake to outgassing during El Niño and vice versa during La Niña events) under the strongest future climate change scenario SSP5-8.5. This reversed relationship, superimposed on the projected ENSO–CO₂ fluxes by the land biosphere (Kim et al., 2016), suggests an even stronger increase in atmospheric CO₂ growth rate during future El Niño events. Nevertheless, our assessment indicates that ESMs that simulate this reversed pattern also simulate considerable bias in the contemporary surface CO${}_{\mathrm{3}}^{\mathrm{2}-}$ concentration; therefore, the projections from these ESMs should be considered with caution.

Readers must keep two things in mind while interpreting the results of this study. First, only the high-emission SSP5-8.5 scenario has been considered. Results may be scenario dependent, especially with respect to the future atmospheric CO₂ level. Second, the models have been grouped (and averaged) into two categories to identify patterns or consistencies and to simplify the analyses. In addition, we have focused our analysis on contrasting El Niño and La Niña for a confined region in the equatorial Pacific (i.e. 2^∘ S–2^∘ N, 180^∘ E–260^∘ E). We have also applied our analysis on a slightly larger domain (5^∘ N–5^∘ S, 150^∘W–240^∘W), and the overall conclusions remain consistent (not shown).

Accurate representations of the tropical Pacific mean climate state and ENSO-related changes in models are fundamental for ENSO impact studies. For instance, ESM projections of future ENSO mode and all related statistics (e.g. Niño 3.4) depend on the mean state biases (Battisti et al., 2019). Simulating the contemporary tropical Pacific climate accurately has been a great challenge for the modelling community over the past few decades, but evidence of continuous improvements over the preceding generation of ESMs is a promising sign (e.g. IPCC, 2021; Bellenger et al., 2014).

We show that the simulated amplitude and spatial extent of physical and biogeochemical properties induced by ENSO vary considerably across ESMs. Future model development should therefore focus on capturing the observed mean state and the regional anomalies pattern during dominant climate modes, such as La Niña versus El Niño phases. To achieve these developments, long-term interior carbon chemistry observations are needed. In particular, vertical distribution of DIC, ALK, and CO₃ concentrations during El Niño and La Niña would be extremely helpful for constraining the contrasting ESM projections.

The important roles of the vertical DIC gradient and biological production in the reversal of the ENSO–CO₂ flux relationship are also highlighted in this study. For example, the increased primary production variability that contributes to the reversed ENSO–CO₂ flux relationship can be associated with model-dependent primary production formulation (e.g. sensitivity of phytoplankton growth rate to temperature) and circulation-driven nutrient upwelling patterns (among others). We note that elucidating the drivers of enhanced primary production in each ESM is beyond the scope of this paper.

Future model developments are also necessary to ensure that ESMs are able to reliably capture multiple layers of non-linear processes that connect ENSO variability and sea–air CO₂ fluxes in the equatorial Pacific. The latest generation of ESMs have progressed considerably in reproducing key climatological properties of surface ocean biogeochemistry (Séférian et al., 2020). Future advancements could focus on improving the biogeochemical representation in the interior and better understanding of the physical and biogeochemical interactions across various timescales and different regions. For instance, outside the tropical Pacific, the ocean carbon cycle is modulated by different climate modes, such as the North Atlantic Oscillation (Keller et al., 2012; Tjiputra et al., 2012) and the Southern Annular Mode (Lenton and Matear, 2007; Keppler and Landschützer, 2019). Future studies that advance our understanding of how the ocean carbon cycle in these regions might be affected by future anthropogenic climate change could be valuable to further reduce uncertainties in future climate projections.

5 Summary

In this paper, the ENSO-induced response of sea–air CO₂ fluxes under a high CO₂ future climate scenario is presented using observed data and model simulations from CMIP6 ESMs. The heart of the work was to examine the roles of two concurrent physical and biogeochemical processes driving the sea–air CO₂ flux variability: (i) anomalously high (low) surface temperature that leads to low (high) CO₂ solubility, which enhances (reduces) outgassing, and (ii) anomalously strong (weak) upwelling that brings more (less) DIC-rich water to the surface and enhances (reduces) outgassing. The opposing effects of these two processes is enhanced by ENSO: high sea surface temperature is associated with weaker upwelling and stronger stratification during El Niño, and the opposite occurs during La Niña.

The findings can be summarized as follows.

• During the historical period, observational data show that sea–air CO₂ flux anomalies are negatively correlated with ENSO-associated warming, and this is reproduced in the vast majority of the models (14 of 16).

• Under the high-emission future projection (SSP5-8.5), this correlation persists in half of the examined models (7 of 14) but is projected to reverse across the other half.

• Depending on the model, the future variability of the CO₂ flux anomaly in the equatorial Pacific domain could either increase or decrease. This is consistent with the projected pCO₂ variability over the same area (Gallego et al., 2020). However, using models selected based on their contemporary period performance, Liao et al. (2021) found weaker future CO₂ flux anomalies during ENSO phases.

• All the models shows a higher Revelle factor in the future, leading to a stronger pCO₂ sensitivity to changes in surface temperature between ENSO phases. This result is consistent and reaffirms findings from previous studies (e.g. Liao et al., 2021; Gallego et al., 2020; Hauck and Völker, 2015);

• In this study, the mechanisms leading to the reversal of this ENSO–CO₂ flux relationship are explained by the thermal contribution to pCO₂ becoming more dominant relative to the non-thermal component. This is explained by (i) the increase in the pCO₂, (ii) the enhanced primary production fluctuation, and (iii) the upper-ocean DIC concentration increase (due to increasing anthropogenic CO₂ uptake), which decreases the vertical gradient in the thermocline and eventually attenuates the ENSO-modulated surface DIC variability.

• A reversing ENSO–CO₂ flux relationship over the 21st century projected in some ESMs seems unlikely since it is a direct consequence of a strong bias in the mean state of carbonate ion concentration over the historical period.