the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Early warnings of the transition to a superrotating atmospheric state
Mark S. Williamson
Timothy M. Lenton
Several general circulation models (GCMs) show bifurcations of their atmospheric state under a broad range of warm climates. These include some of the more extreme global warming scenarios. This bifurcation can cause the transition to a superrotating state, a state where its angular momentum exceeds the solid body rotation of the planet. Here we use an idealised GCM to simulate this transition by altering a single non-dimensional control parameter, the thermal Rossby number. For a bifurcation-induced transition there is potential for early warnings, and we look for these here. Typically used early warning indicators, variance and lag-1 autocorrelation, calculated for the mean zonal equatorial wind speed, increase and peak just before the transition. The full autocorrelation function taken at multiple lags is also oscillatory, with a period of 25 d preceding the transition. This oscillatory behaviour is reminiscent of a local supercritical Hopf bifurcation. Motivated by this extra structure, we use a generalised early warning vector technique based on principal oscillation patterns (POPs) to diagnose the dominant spatial modes of the horizontal wind field fluctuations. We find a zonal-wavenumber-0 pattern that we call the “precursor” mode that appears shortly before and disappears soon after the transition. We attribute the increase in the early warning indicators to this spatial precursor mode. This mode is correlated to oscillations in strength of the Hadley cells. Following the transition, an eastward-propagating zonal-wavenumber-1 mode of period ∼4 d dominates the dynamics. This mode appears to be representative of the Kelvin–Rossby instability others have previously identified. Although the control parameter used to simulate the transition is unlikely to be relevant to future climate change, the Kelvin–Rossby transition mechanism may well be relevant, and the simulations reported here do show early warnings and serve as a test bed for whether we can detect this transition before it happens.
- Article
(13986 KB) - Full-text XML
- BibTeX
- EndNote
Abrupt transitions in the climate often go by the name “tipping points”, and early warnings of such tipping points are currently an active area of research (Scheffer et al., 2009; Lenton, 2011; Scheffer et al., 2012). The IPCC has defined a tipping point as a “critical threshold beyond which a system reorganises, often abruptly and/or irreversibly” (IPCC, 2023) and “for the climate system, the term refers to a critical threshold at which global or regional climate changes from one stable state to another stable state” (IPCC, 2019). One such example is the Atlantic meridional overturning circulation (AMOC), which can abruptly change from an “on” to “off” state as freshwater flux into the North Atlantic is increased (Stommel, 1961; Vellinga and Wood, 2002; Mecking et al., 2016). There are a variety of other postulated climate tipping elements, including the Amazon rainforest, Greenland ice sheet and West Antarctic ice sheet. Changes in atmospheric circulation patterns under anthropogenic climate change are also interesting possible candidates for tipping points, with the 3D nature of atmospheric circulation presenting possibilities of novel early warning signals (EWSs) (Tantet et al., 2015). For example, the West African monsoon is sometimes classified as a tipping system (Loriani et al., 2023), leading to very different vegetation states, e.g. the “green Sahara” (Brovkin et al., 1998). The transition to an atmospheric superrotating state in warm climates is another possible tipping point. Here we look at whether there are EWSs of the tipping point to superrotation in an idealised scenario. However, the extension of EWSs we use is more generally applicable as an approach to detecting precursors of bifurcation-induced changes in state in any spatially extended or coupled system.
Mathematically, tipping points can be described by several kinds of transitions. (a) Noise-induced transitions are probabilistic transitions between multiple steady states induced by large-amplitude noise, with large here meaning that the probability of a perturbation large enough to push the system into a different attractor over the timescale of interest is non-negligible. These events have limited predictability (Ditlevsen and Johnsen, 2010). (b) Rate-induced transitions occur when the disturbance is too fast for the system to remain sitting in its current attractor, resulting in a jump to a new stable state (Ashwin et al., 2012; Wieczorek et al., 2010; Feudel, 2023). (c) Bifurcation-induced transitions occur when the current system state becomes unstable at the bifurcation as the disturbance (or control parameter) is slowly changed. The system will then transition to a new stable state. It is the third type, tipping due to a bifurcation, which has received the most attention, as there is potential for early warnings of this sort of transition (Wiesenfeld, 1985; Held and Kleinen, 2004; Livina and Lenton, 2007; Dakos et al., 2008; Lenton et al., 2012). A bifurcation of states has been reported for the atmosphere when it transitions to a superrotating state (Suarez and Duffy, 1992; Saravanan, 1993; Shell and Held, 2004; Arnold et al., 2012; Herbert et al., 2020).
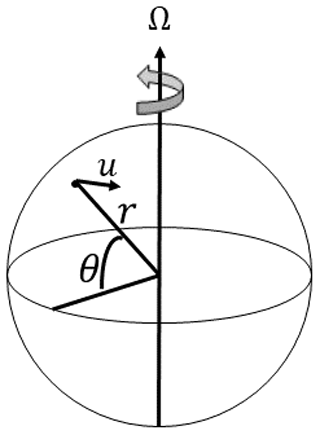
Figure 1Schematic of the variables used to describe a superrotating atmospheric state on a planet of radius r rotating with angular velocity Ω. θ is the latitude taken relative to the Equator, and u is the zonal horizontal velocity of the atmosphere in the planet's rotating frame.
An atmospheric superrotating state is said to occur when the atmosphere rotates quicker than the planet beneath it or (more precisely) when the zonal angular momentum of the atmosphere exceeds the angular momentum from the solid-body rotation of the planet. The solid-body angular momentum per unit mass LE at latitude θ of a planet rotating at angular velocity Ω with radius r is (see Fig. 1)
For a shallow atmosphere moving with zonal velocity u at latitude θ measured in the planet's rotating frame, the angular momentum per unit mass L is given by
A superrotating state occurs when for some θ. LE is maximal at the Equator (θ=0), giving . For superrotation the zonal velocity of the atmosphere u must be greater than the right-hand side of the following equation:
This condition has a minimum u at the Equator (θ=0) where zonal velocity need only be positive (u>0). Moving away from the Equator () the zonal velocity required for superrotation increases steeply. If it occurs, superrotation will almost certainly be present at the Equator as superrotation at a higher latitudes would result in inertially unstable atmospheric configurations. What this means for Earth rotating west to east is that the prevailing easterlies at the Equator (u<0) change to prevailing westerlies. We label the bound for superrotation uSR, which is found using the following equation:
Superrotating atmospheres exist on Venus and Titan (Read and Lebonnois, 2018), and they may have occurred on Earth in warmer, past climates. Caballero and Huber (2010) showed a full-complexity general circulation model (GCM) that transitioned to a superrotating state when equatorial surface temperatures got sufficiently high, within the range of temperatures thought to have existed in the early Cenozoic period of Earth's history (65 million years ago). This was a period where it was around 10 °C warmer on average than today. The atmospheres of other warmer periods such as the early Pliocene and Eocene may also have been superrotating (Tziperman and Farrell, 2009). Simulations of warm climates that generate enhanced tropical convective variability seem particularly prone to superrotation (Arnold et al., 2012), as do those where convective heating strengthens (Laraia and Schneider, 2015). This has led to the hypothesis that it may be relevant to future climate projections (Held, 1999; Pierrehumbert, 2000) and account for the superrotation seen in extreme global warming simulations (Huang et al., 2001). Even though the probability of transitioning to a surface superrotating state is presently thought to be low as the Earth warms into the future (Caballero and Carlson, 2018), the possibility is a high risk. For example, if the prevailing Pacific equatorial westerlies switched to the easterlies of an atmosphere with superrotation at the surface, a permanent El Niño state would result, along with all of the global impacts that this would entail (Pierrehumbert, 2000). Tziperman and Farrell (2009) used this mechanism to explain the permanent El Niño state that is thought to have existed in the Pliocene. Although surface superrotation seems unlikely, superrotation happens readily in the upper troposphere under high-end global warming scenarios. The impact on surface climate would, however, be less severe (Caballero and Carlson, 2018).
Superrotation implies the atmospheric angular momentum locally exceeds that provided by the planet surface. This can only be achieved through an up-gradient momentum flux that is in excess or balances the removal of momentum by the poleward large-scale meridional circulation and the zonal-mean drag due to viscosity (Caballero and Carlson, 2018). This up-gradient flux can be supplied by non-axisymmetric eddies (Hide, 1969; Gierasch, 1975; Read, 1986). There are many studies that examine the eddy dynamics responsible for superrotation, of which there are two broad categories, although horizontal momentum transport by off-equatorial waves feature in both (i) generation through non-axisymmetric forcing (Scott and Polvani, 2008; Saravanan, 1993; Suarez and Duffy, 1992; Arnold et al., 2012; Shell and Held, 2004) and (ii) generation through barotropic, baroclinic or Kelvin–Rossby instability (Williams, 2003; Wang and Mitchell, 2014; Mitchell and Vallis, 2010; Zurita-Gotor and Held, 2018; Zurita-Gotor et al., 2022). It is the second category that is relevant to this paper, in particular the Kelvin–Rossby instability mechanism. Theoretical work on this mechanism (Wang and Mitchell, 2014; Zurita-Gotor and Held, 2018; Zurita-Gotor et al., 2022) shows the transition is via a loss of stability and so there should be early warning signals. In this mechanism, superrotation arises from the wave–mean-flow interaction, specifically the interaction of equatorial Kelvin waves and off-equatorial Rossby waves that mutually amplify each other and generate a planetary-scale mode that converges zonal momentum onto the Equator. Zurita-Gotor et al. (2022) show that the Kelvin–Rossby coupling is a viable mechanism for producing terrestrial superrotation and may explain the warm-climate superrotation found by Caballero and Huber (2010).
Transitions to superrotating states may be smooth (Huang et al., 2001; Caballero and Huber, 2010; Mitchell and Vallis, 2010) or abrupt (Suarez and Duffy, 1992; Saravanan, 1993; Arnold et al., 2012; Zurita-Gotor et al., 2022). The smooth, gradual type seems to be more common in simulations of global warming scenarios or warm paleoclimates with comprehensive, multilevel GCMs (Arnold et al., 2012). Abrupt transitions are seen more commonly in models with some degree of idealisation; however, that does not rule them out in more realistic scenarios (Held, 2016). The original example of an abrupt transition to a superrotating state was found by Suarez and Duffy (1992) in a two-layer GCM as the tropical heating was increased. This transition also showed hysteresis, meaning that as the tropical heating was reversed below the transition's critical value, the superrotating state persisted to a new and lower critical value. Arnold et al. (2012) have found similar behaviour in a higher-resolution and multilevel (albeit still idealised) GCM. This bistability is something we will also investigate in a different setting in this paper.
Tipping points and bifurcation-induced transitions are often, but not necessarily, abrupt (Armstrong McKay et al., 2022). Transcritical, supercritical pitchfork and supercritical Hopf bifurcations (Strogatz, 2001) are examples that result in smooth transitions but have early warnings due to the loss of stability of the local state. The transition to superrotation reported here is smooth. Nevertheless, early warnings of the transition are shown, and therefore these simulations serve as a test bed for whether we can detect this transition before it happens.
In this paper the focus will be the fluctuations around the mean wind field state and how their properties change as the atmosphere gets closer to a superrotating state, the idea being that these properties can serve as early warnings of the transition. We first introduce the idealised GCM used for these numerical simulations and the control parameter we vary to span Earth-like to fully superrotating atmospheric states in Sect. 2. We then describe this range of simulated mean atmospheric states in Sect. 3 before going to the main focus of the paper: early warnings of the transition. We start by calculating the widely used early warning indicators in Sect. 4. Motivated by the bistability in the superrotating states observed in the experiments of Suarez and Duffy (1992) and others, we look for multiple co-existing states with our control parameter in Sect. 5. In Sect. 6, we generalise the usual scalar early warning indicators to the vector setting by calculating the principal oscillation patterns (POPs). This allows us to diagnose the dominant spatial patterns in the wind field fluctuations preceding the superrotation transition and the dominant patterns following the transition. We discuss our results and make conclusions in Sect. 7.
We use an idealised general circulation model (GCM) to simulate the transition to superrotation. The model framework we use is Isca (Vallis et al., 2018), which is based on a spectral dry dynamical core obeying the primitive equations of motion of Gordon and Stern (1982). Isca is designed to be highly configurable for use in exoplanet research in terms of both complexity (multiple radiation schemes and moist or dry atmospheres are options) and parameter values (planetary radius, rotation rate and fluid density are among the many values that can be altered). The configuration we use here is as simplified as possible and follows the approach of Mitchell and Vallis (2010) closely. Simulations are performed at T42 resolution (about 2.8° resolution at the Equator) and with 25 vertical sigma levels (equal pressure levels , where p is pressure and ps is surface pressure).
The surface of the planet is prescribed to be isotropically smooth with no topography or continents present. No radiation scheme is used either. Instead temperature is linearly relaxed to a prescribed mean annual average state (Newtonian cooling) using the scheme of Held and Suarez (1994). In particular, the surface temperature is relaxed to the zonally symmetric profile
with T0 being the lowest-level temperature and the global average surface temperature. ΔH is a non-dimensional parameter specifying the pole–Equator temperature difference. The vertical temperature is assumed to relax to a moist adiabat with lapse rate 6 K km−1 capped at a minimum of 200 K in the stratosphere. The radiative relaxation time is 40 d in the free troposphere and approximately 4 d in the boundary layer, the top of which is fixed at σ=0.7 (see Held and Suarez, 1994, for the full functional forms). As previously mentioned, we follow Mitchell and Vallis (2010) closely, although there are some minor differences: Mitchell and Vallis (2010) use K and ΔH=0.2, here we use K and ΔH=0.215. As both of these parameters combine together in a non-dimensional number that will be used as the control parameter in numerical experiments (the thermal Rossby number; see below), these small differences should be negligible in comparing our results with theirs.
Friction from the planet's surface on the atmosphere relaxes horizontal velocities back towards zero in the atmospheric boundary layer, and this is specified as an extra, linear and vertical-height-dependent (Rayleigh) drag term in the equation for the horizontal velocity. This extra drag term is applied as
where v is a vector of the horizontal velocities . For the full horizontal momentum equations, see Mitchell and Vallis (2010). The reciprocal of the Rayleigh relaxation time, kf, is taken to be 0.5 d−1 at the planet surface (σ=1) and linearly decreases to zero at the top of the boundary layer at σb=0.7. This is slightly smaller than the value of 1 d−1 used in Mitchell and Vallis (2010).
The horizontal momentum equations governing the atmospheric dynamics simplify in non-dimensional form when subject to Rayleigh friction and Newtonian cooling. These equations are then governed by just a few non-dimensional parameters. The relevant non-dimensional parameter that is varied in the experiments here and in Mitchell and Vallis (2010) is the thermal Rossby number:
R here is the specific gas constant for dry air (287 J K−1 kg−1). However, as the numerical model code is dimensional, a dimensional parameter must be varied, and here the planetary radius r has been chosen for this purpose. By making this choice, the other non-dimensional parameters, the Ekman number and thermal relaxation time, remain unaltered.
Strictly RoT as given by Eq. (8) varies with latitude. However, in the following experiments we attribute a single value of RoT to each simulation by replacing T0 with the average temperature , i.e. in Eq. (8), which is the average thermal Rossby number over the whole planet.
To summarise, in the following experiments we vary the thermal Rossby number to go from Earth-like atmospheric states through the transition to a fully superrotating state by changing the planetary radius r for each simulation. All other parameters will remain fixed. Each simulation is initialised from a homogenous atmospheric state and integrated for either 3 or 10 years (1080 or 3600 d, respectively). A stationary state is reached after approximately 200 d. In the following results we use the last 2 years of the 3-year simulation unless stated otherwise.
In Fig. 2, we plot the mean zonal and vertical structure of the atmosphere at selected values of RoT. The coloured line contours show the zonal time mean wind speed u with latitude θ and height after the atmosphere has reached a stationary state (the last 2 years of a 3-year integration). The red line contours show regions of u>0, the blue line contours show regions of u<0 and the black line contour marks u=0. Line contours are spaced at 5 m s−1 intervals. The region enclosed by the dotted black line is superrotating, meaning that it marks the region where u=uSR (Eq. 4) and is centred at the Equator. The filled contours show the mean meridional overturning.
We start simulations at Earth-like values of the control parameter (RoT=0.02, Fig. 2a) and incrementally increase it through the transition. No superrotation at any vertical level is present in the Earth-like simulation. The transition occurs first in the upper troposphere near the tropopause. This first transition is around RoT∼0.07 (Fig. 2c, dotted black region at the Equator around σ=0.2). We will refer to this as the first transition to an equatorial superrotating state. This small superrotating region then extends further downwards into the troposphere, upwards in the stratosphere and out into higher latitudes as RoT is increased (Fig. 2d–f).
Superrotation is present at RoT=0.87 (Fig. 2e) in the majority of the equatorial troposphere and lower stratosphere above the height of the boundary layer (σ=0.7) but absent within it. For RoT>0.87 (Fig. 2f), the third-lowest vertical level in the model also starts to superrotate at the Equator. For all simulations we have investigated (RoT≤11.4), this is the lowest vertical level that superrotates and marks the final vertical transition. We will refer to this as the final transition to an equatorial superrotating state. All of the troposphere at σ<0.8 (and some of the stratosphere) is superrotating after this point. We study this final transition at the lowest altitude that becomes superrotating in some detail in this paper. This lowest vertical level, the third vertical level is at σ=(0.7 0.79], with a mid-point at σ=0.74, and this level lies at a vertical height of ∼1–2 km above sea level.
As previously mentioned, none of the simulations show superrotation in the two lowest vertical levels (σ>0.8). This could be due to Rayleigh drag within the boundary layer (σ≥0.7) decelerating the horizontal flow and acting as a negative angular momentum flux for any u>0. However, the final transition occurs at a level within the atmospheric boundary layer, and thus it still experiences a small amount of drag. However, surface superrotation has been shown to occur in small parameter regimes (Caballero and Carlson, 2018) and is not commonly seen in GCM simulations.
Other notable features are the midlatitude jets (the largest-value red line contours in Fig. 2) in the Earth-like simulation centred at σ∼0.3 and at latitude °. These jets tend to move poleward as RoT increases. The mean meridional overturning circulation (filled contours in Fig. 2) also tends to reduce in intensity with increasing RoT.
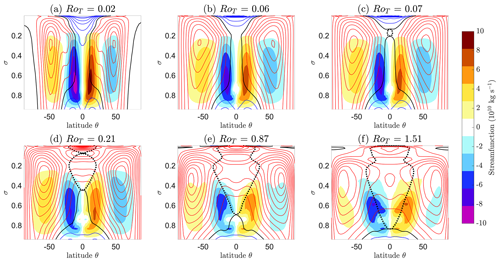
Figure 2Mean vertical and zonal structure of the atmosphere at various values of the control parameter RoT. Zonal mean u with latitude and vertical height is shown as coloured line contours: u>0 contours are shown as red lines, the u=0 contour is the black line and u<0 contours are shown as blue lines. Contour lines are spaced at 5 m s−1 intervals. The region enclosed by the dotted black line is superrotating (c–f). This means that it marks the region where u=uSR (Eq. 4). The filled contours show the mean meridional overturning as given by the mass streamfunction, with blue and red regions having anti-clockwise and clockwise circulation, respectively. An Earth-like state is shown in (a) (RoT=0.02). (b) A state close to the first superrotation transition. (c) A small region in the equatorial upper troposphere that becomes superrotating. This region expands further down into the troposphere and up into the stratosphere as RoT increases (d–f). Panel (e) shows the zonal-mean atmospheric state just before the third-lowest vertical level becomes superrotating. This is the lowest level that superrotates, at least for RoT∼O(1), and it marks the final transition. In (f) all of the troposphere σ<0.8 is superrotating.
We also show snapshots t=900 d into the simulation of the horizontal wind field () at the two vertical levels where the first and final transitions occur (σ=0.19 and σ=0.74, respectively) for various key values of the control parameter RoT in Fig. 3. Earth-like simulations are shown in Fig. 3a and b. The midlatitude instabilities are evident, as is the lack of superrotation at the Equator (blue shading). In Fig. 3c, the wind field just before the first transition is shown at the vertical level it occurs at (RoT=0.06, σ=0.19). There is a roughly equal mixture of red and blue shading giving a zero mean zonal u. Lower levels are not showing equatorial superrotation at this value of RoT (Fig. 3d). Figure 3f shows the wind field just before the final transition at the vertical level it occurs at (RoT=0.87, σ=0.74). Again, there is a roughly equal mixture of red and blue shading, giving zero mean zonal u. Figure 3e, g and h are all fully superrotating equatorial states (mainly red shading).
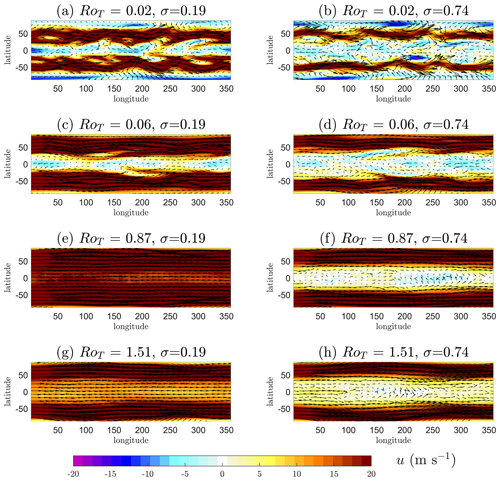
Figure 3Snapshots (t=900 d into each simulation) of the horizontal wind field (shown as arrows) at the two vertical levels σ=0.19 and σ=0.74. These vertical levels correspond to the first transition to superrotation at RoT∼0.07 and the final transition at RoT≳0.87, respectively. The underlying colour plot shows the u component of this field, with reds corresponding to u>0 and blues to u<0 (u=0 is white). Panels (a) and (b) show an Earth-like state. Panel (c) shows the wind field just before the first transition at the vertical level it occurs at. Panel (f) shows the wind field just before the final transition at the vertical level it occurs at. Panels (e), (g) and (h) show fully superrotating equatorial wind field states (predominately red colours at the Equator).
More information on the mean states and the mechanisms of superrotation in these simulations is reported in Mitchell and Vallis (2010). From here on we get to the main focus of this paper, namely that we study the fluctuations around the mean states and their properties as precursors to the transitions.
In this section we calculate early warning signals (EWSs) for the varying RoT simulations with the aim of early detection of the transition to a superrotating state. These indicators are widely used to detect abrupt transitions resulting from local bifurcations (Lenton, 2011; Thompson and Sieber, 2011). Typically, these are designed to detect the increasing recovery time and amplitude of small fluctuations δx(t) around the mean stationary state, denoted as , of some scalar state parameter x(t) that is a function of time t. The state of the system is therefore given by
and it is often assumed to evolve autonomously according to some function f(x) as (overdots denote ordinary time derivatives, i.e. ). f(x) is a non-linear function of x in general. Provided the fluctuations are not too large, one can approximate the dynamics well by performing Taylor expansion on f(x) to the first order around the mean state, i.e. , where the Jacobian is given by . In this case the dynamics of the fluctuations can be approximated with a linear first-order ordinary differential equation (ODE), i.e.
For a time-invariant mean state (and time-invariant J(x)), this simple ODE has the solution
There are three possible fates of an initial fluctuation in amplitude δx(0) depending on the sign of the real part of . (i) The real part of is negative (), the initial fluctuation δx(0) decays and the system state will be stable to perturbations eventually recovering to . In this case a recovery or e-folding time can be defined as the time taken, τ, for the fluctuation to reach th of its initial value as . (ii) The real part of is positive (), any initial fluctuation will get exponentially larger with time and the system will not recover to , i.e. is unstable. (iii) The real part of is zero, i.e. . In this case, perturbations will not grow or decay. This neutral stability occurs at a bifurcation.
Early warning indicators are designed to detect the increasingly less negative value of or equivalently the increasing system recovery time τ as it approaches the bifurcation. This phenomenon is termed “critical slowing down”. One popular indicator is the variance Var(x) of x with time
where E[.] is the expectation value. For the case where x is a scalar variable with first-order dynamics subject to random (white-noise) forcing (an Ornstein–Uhlenbeck process), J(x) is also a real scalar, and the variance is given by
This measures the mean amplitude of the system fluctuations to a random forcing of mean amplitude σQ (σQ is generally assumed to be constant as the bifurcation is approached). The state becomes less stable closer to the bifurcation, and gets less negative, showing up in the indicator as an increase in variance.
White-noise forcing is often assumed to approximate internally generated fast-timescale chaotic weather variability when applied to climate applications, such as early warning indicators, empirical orthogonal functions and linear regressions (von Storch and Zwiers, 1999), and this is also what we do throughout this paper.
Another popular early warning indicator is time-lagged autocorrelation
which measures the recovery time of the system to perturbations. Again, for the case where x is a real scalar variable with first-order dynamics subject to random (white-noise) forcing, is a negative real number if the state is stable, and α(tlag) is just an exponentially decaying function of tlag. As a bifurcation is approached and the indicators σx→∞ and α(tlag)→1.
The temporal evolution of a scalar state variable x described by a linear first-order ODE is constrained to only permit exponential decay from a perturbation. However, a real-valued state variable x may have oscillatory behaviour and therefore must be described by higher-order ODEs. In this case α(tlag) may have a more complicated functional form. For example, a system with second-order dynamics can have an autocorrelation function with an oscillatory term. Relevant to our case is the approach to a Hopf bifurcation, whose α(tlag) has the generic form (Bury et al., 2020)
For a real-valued J(x) to describe a Hopf bifurcation, it must be at least a two by two (non-symmetric) matrix with complex eigenvalues, λ and λ*, that appear in conjugate pairs (the * denotes complex conjugation). The real part of the complex eigenvalues of J(x) () determines the exponential decay envelope of the autocorrelation function. This envelope decays over a longer timescale as the bifurcation is approached. Within this envelope there may also be oscillations, whose frequency is given by the imaginary part of J(x), ω=ℐ(λ).
In most studies, the full autocorrelation function at all values of tlag is generally not used. It is usually the value of the autocorrelation function at tlag=1 (the lag-1 autocorrelation) that is used. This often works well as it is more robust to sample size and signal to noise provided the oscillation period, , is large compared to the value of tlag that is used to evaluate α(tlag). Formally, if ωtlag≪1, then Eq. 16 approximates to ; i.e. it is a good indicator of the real part of the Jacobian eigenvalues and therefore of critical slowing down.
We will also use the autocovariance function, R(tlag), which encodes information of both variance and autocorrelation, giving
or . The variance is just given by R(0) and .
4.1 Temporal EWSs of the superrotation transition
We apply these early warning indicators to study the transition to superrotation at vertical level σ as follows. We look at the statistics of the fluctuations, δu(σ,t), around the mean zonal wind field state, , where is the time- and area-weighted spatial mean of a spherical segment centred on the Equator at vertical height σ with edges at ° latitude. An equatorial band centred on the Equator is chosen to analyse the zonal wind field u because, as previously discussed, this is the most likely place to observe superrotation if it occurs. Formally, we compute R(σ,tlag) for where
where ϕ is the longitude and is the area of the spherical segment. We choose a section of the time series u(σ,t) starting at a time ts that is sufficiently after the simulation spinup so that the atmosphere is in an approximately stationary state. In the model configuration used, the atmosphere reaches a steady state after roughly 200 d, although we use ts=361 d. The finish time tf is chosen to be large for accurate determination of the statistical estimators. Ideally this would be tf→∞; however, due to computational time we mostly limit this to tf=1080 d. However, when studying the first transition we have performed longer simulations (10 years) to better resolve the long timescales present around the tropopause and set tf=3600 d; u(σ,t) is then averaged over a period to give
In Fig. 4, is shown as it varies with vertical height σ and the control parameter RoT.
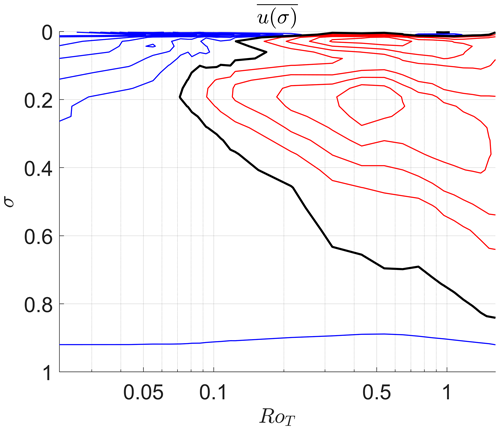
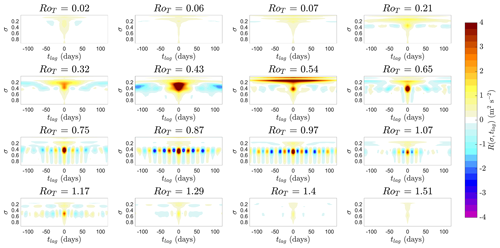
Figure 4Here we show in an equatorial band with edges at ±10° latitude as it varies with vertical height σ and control parameter RoT. Red contours show positive . Blue contours show negative . Both are spaced at 5 m s−1 intervals. The black line denotes the zero contour and approximately marks the boundary between superrotating and non-superrotating regions.
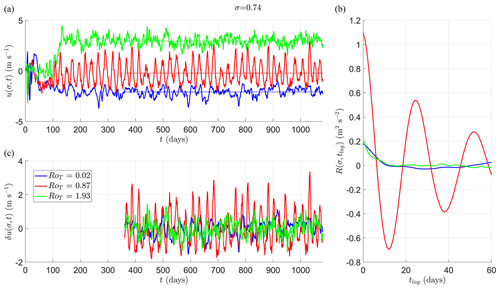
Figure 5Mean u around an equatorial band at vertical height σ=0.74. (a) Mean zonal wind speed u(σ,t) in a spherical segment centred on the Equator and with edges at ±10° latitude during a 3-year simulation (1080 d). Different colours correspond to a simulation with a different value of RoT. We also show highlighted values of RoT∈{0.02 (blue) 0.87 (red) 1.93 (green)}. In (c) we show , which shows the fluctuations in u(σ,t) around the temporal mean over the last 2 years of the simulation as a function of RoT. Dotted lines indicate . (b) The autocovariance function R(σ,tlag) as a function of tlag. This function is oscillatory for RoT=0.87 (red line) just before the final transition.
4.1.1 Final transition: RoT∼0.87 at σ=0.74
The final transition where the majority of the equatorial troposphere (σ<0.8) starts to superrotate occurs at RoT∼0.87. In this subsection the statistics of δu(σ,t) at σ=0.74 are analysed. This corresponds to the third-lowest vertical level in the model. We look for early warnings of the first transition in the following subsection.
In Fig. 5a, we plot the time series for selected values of RoT (0.02 is blue (Earth-like), 0.87 is red (close to the final transition) and 1.93 is green (fully superrotating)) over the 3-year simulation period. The mean u(σ,t) over the last 2 years () is plotted as a corresponding dotted coloured line. In Fig. 5c we show the fluctuations around the mean, δu(σ,t), as a function of RoT. The larger, oscillatory response of u(σ,t) close to the final transition is clearly visible in the time series. The time series looks much more random and akin to first-order noisy dynamics (such as an Ornstein–Uhlenbeck process) on either side of the final transition (blue and green).
In Fig. 5b we have plotted the autocovariance function (Eq. 17), , for each of the three selected RoT values during the last 2 years of each simulation. The value at tlag=0 is equivalent to the variance of u, Var(u). One can see close to the transition (red) that variance is much higher than either side of the transition (green and blue). One can also see the functional form of R(σ,tlag) is also very different close to the transition, showing an oscillation of around 25 d contained in an exponential decay envelope with an e-folding time of approximately τ∼35 d (see Eq. 16). In contrast, the response of u(σ,t) to perturbations is neither oscillatory nor long lasting on either side of the final transition.
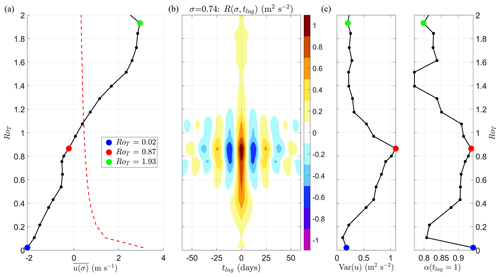
Figure 6Early warning indicators of the final transition at σ=0.74. Each dot is an individual simulation. Coloured dots correspond to the same coloured simulations in Fig. 5. (a) Mean zonal wind speed in a spherical segment centred on the Equator with edges at ±10° latitude during the last 2 years of the simulation against RoT at vertical height σ=0.74. The dotted red line is the threshold for superrotation to occur (uSR). This is non-zero as the wind speed is averaged over a non-zero-thickness latitude band. (c) Typical early warning indicators of a local bifurcation: with the left-hand plot showing the variance of mean zonal u(σ,t) and the right-hand plot showing lag-1 autocorrelation of mean zonal u(σ,t). (b) Autocovariance function R(σ,tlag) and how it changes with RoT (y axis) and tlag. Oscillations of the 25 d period appear for values of RoT∼[0.5 1.2] and have a maximum in amplitude around RoT∼0.9.
In Fig. 6a we plot in the equatorial spherical segment against RoT. Black dots are individual simulations, and black lines connect these values. The dotted red line is the threshold required for superrotation, uSR; see Eq. (4). This is larger than the zero bound required for superrotation at the Equator due to the finite latitude width of the spherical segment. Superrotation at this vertical level occurs approximately for RoT>1. Interestingly, this plot is not monotonically increasing with RoT – there is a local maximum at RoT∼0.54 followed by a plateau to RoT∼0.75 below the superrotation threshold. There is another local (and global) maximum in around RoT∼1.9 when the atmosphere is in a fully superrotating state. In Fig. 6c we plot the usual early warning indicators, variance of u(σ,t) (left-hand plot, Var(u)) and lag-1 autocorrelation (right-hand plot, α(tlag=1 d)). Both indicators peak at RoT=0.87, just below , suggesting this is where the atmospheric state at this vertical level is least stable.
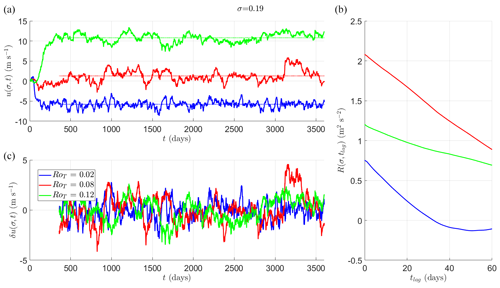
Figure 7Mean u around an equatorial band at vertical height σ=0.19. (a) Mean zonal wind speed u(σ,t) in a spherical segment centred on the Equator and with edges at ±10° latitude during a 10-year simulation (3600 d). Different colours correspond to a simulation with a different value of RoT. We also show highlighted values of RoT∈{0.02 (blue) 0.08 (red) 0.12 (green)}. In (c) we show , which gives the fluctuations in u(σ,t) around the temporal mean over the last 9 years of the simulation as a function of RoT. Dotted lines indicate . (b) The autocovariance function R(σ,tlag) as a function of tlag. All of these functions have slow decay timescales, indicating very lightly restored or unstable regions, as can be seen from the meandering time series in (a) and (c).
There is an initially high value of lag-1 autocorrelation when RoT=0.02 is at an Earth-like value, and this looks like an outlier when compared to the other simulations in Fig. 6c. The full (multiple lag) autocorrelation function of this simulation as shown in Fig. 5b in blue is not oscillatory or with high variance, but it does not look like a typical exponentially decaying function like the other simulations performed here. It has an approximate linear decay with increasing tlag. As the autocorrelation is assumed to be an exponentially decaying function of tlag, lag-1 autocorrelation may not be the best way to infer the decay timescale (and critical slowing down) for this particular value of RoT. The mean equatorial zonal flow may be in a different regime compared to the other simulations as RoT is increased.
As shown in Fig. 5b, the autocorrelation function is not necessarily only exponentially decaying with increasing tlag as required for lag-1 autocorrelation to be a good indicator of the stability of the state. However, as argued in Sect. 4, it is a good indicator for an oscillatory autocorrelation function provided ωtlag is much smaller than 1. In this case , meaning that taking α(tlag=1 d) should be sufficient for those oscillatory functions.
Motivated by the extra information in multiple tlag values of the autocovariance function close to the final transition, we plot R(σ,tlag) in Fig. 6b as it varies with RoT. As previously mentioned, R(σ,tlag) encodes both variance (R(σ,0)) and lag-1 autocorrelation () as limiting cases, making R(σ,tlag) a more complete information source and early warning precursor. R(σ,tlag) is an even function around tlag with a maximal value at R(σ,0).
For values of RoT<0.57 and RoT>1.2, R(σ,tlag) is monotonically decreasing with much like the exponential decay expected for first-order dynamics. Oscillations in R(σ,tlag) start at RoT∼0.57 and remain until RoT∼1.2. The start of the oscillations coincides with the start of the plateau in . The end of the oscillatory phase coincides with the time when the full spherical segment begins to superrotate ( as shown by the dotted red line). Oscillations reach a maximum in amplitude at RoT∼0.87 just before . Throughout the range of their existence, the oscillations have a constant period of approximately 25 d.
4.1.2 First transition: RoT∼0.07 at σ∼0.2
The atmosphere first becomes superrotating at the Equator just below the tropopause (σ=0.19) at RoT∼0.07. We look at the statistics of δu(σ,t) at σ=0.19 in this subsection. This corresponds to the 14th-lowest vertical level in the model. We look at the last 9 years of a 10-year integration. We have performed longer simulations around the point of the first transition because of the long timescales that are present around the tropopause.
Similar to Fig. 5, in Fig. 7a, is shown near the tropopause (σ=0.19) with varying RoT. In Fig. 7b we show the autocovariance function. All time series are very meandering, appearing to be weakly guided random walks when compared to the time series at lower vertical levels.
In Fig. 8, in the equatorial spherical segment against RoT is shown. Superrotation at this vertical level occurs approximately for RoT>0.08. In Fig. 8b and c we plot the usual early warning indicators, variance of u(σ,t) (upper RH, Var(u)) and lag-1 autocorrelation (lower RH, α(tlag=1 d)). Both indicators peak just before RoT=0.08; however, the results are less convincing than the EWSs of the final transition in the preceding section. As mentioned in Sect. 1, previous work has shown this transition is due to a loss of stability, and therefore it should be detectable by an increase in the EWSs. However, the decay timescales at this vertical height in the atmosphere are long (O(100) d), and thus they may require long time series to detect changes in EWSs reliably. For example, the typical values of α(tlag=1) corresponded to an e-folding time of O(100) d. Compare this to the e-folding timescales in the lower troposphere, which are an order of magnitude smaller (O(10) d). Changes may also occur over a small range of RoT that we have not resolved well with the simulations performed.
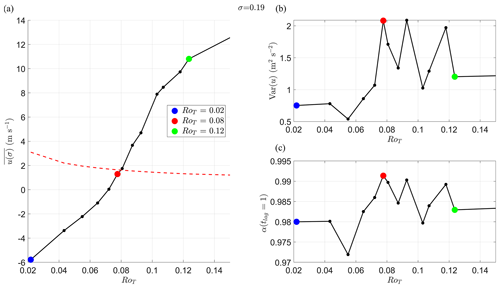
Figure 8Early warning indicators of the first transition at σ=0.19. Each dot is an individual simulation. Coloured dots correspond to the same coloured simulations in Fig. 7. (a) Mean zonal wind speed in a spherical segment centred on the Equator with edges at ±10° latitude during the last 9 years of the simulation against RoT at vertical height σ=0.19. The dotted red line is the threshold for superrotation to occur (uSR). This is nonzero as the wind speed is averaged over a non-zero thickness latitude band. (b, c) Typical early warning indicators of a local bifurcation: (b) variance of mean zonal u(σ,t) and (c) lag-1 autocorrelation of mean zonal u(σ,t).
4.1.3 Full vertical structure
In Fig. 9, the full vertical structure of the autocovariance function of the zonal mean u in the equatorial band, R(σ,tlag), is shown. The oscillations of 25 d period found in R(σ,tlag) that peaked in amplitude around the final transition at σ=0.74 and RoT=0.87 are found throughout the lower troposphere (σ>0.3) between values of . These oscillations have their highest amplitude at RoT=0.87, σ∼0.45. They have roughly the same period as vertical height, and RoT varies throughout their existence. Oscillations are found up to roughly the height of the top of the Hadley cells (σ∼0.3). We have found the oscillations in zonal mean u are also correlated with the strength of the Hadley cells in particular. Larger zonal mean u is simultaneously correlated with a weaker streamfunction in both the Northern Hemisphere and Southern Hemisphere Hadley cells. Conventional Hadley cells with ascent at the Equator are known to flux momentum out of the equatorial region, and this appears to be happening here. The transition to this oscillatory phase of the lower troposphere at RoT>0.54 is accompanied by a large increase in decay timescale around the tropopause (σ=0.19) at RoT=0.54.
As previously mentioned, Suarez and Duffy (1992) found an abrupt transition to a superrotating state in a two-layer GCM when the tropical heating was increased above a critical value. This tropical heating term was their control parameter and is different to the control parameter we alter in these experiments (the thermal Rossby number). Not only was the transition Suarez and Duffy (1992) found to be abrupt, unlike the transition in this paper that seems smooth, but the mean state also showed bistability, meaning that two stable states exist for the same value of the control parameter. By slowly changing their control parameter across the transition's critical value from non-superrotating to a superrotating state and then slowly reversing the control parameter back again below the critical value, the superrotating state persisted to a new and lower critical value. This showed that there was a bistable region in which stable superrotating and non-superrotating states can coexist. Unlike Suarez and Duffy (1992) we find no evidence of bistability in the mean equatorial zonal wind speed, although there is evidence of “flickering” (Dakos et al., 2013), meaning a range of RoT where there are noise-induced transitions between two stable states.
To investigate whether bistability like that found in Suarez and Duffy (1992) is present, we look at the final transition at vertical height σ=0.74. We slowly increase the value of RoT=0.11 through the final transition at RoT∼1 and continue up to RoT=1.64. We will refer to this part of the simulation as the “ramp up”. RoT is then slowly decreased from 1.64 back down to RoT=0.11 at the same rate. We will refer to this part of the simulation as the “ramp down”. As in the fixed RoT simulations, the magnitude of RoT is changed by altering the planetary radius r. Rather than a continuous change in RoT, we step RoT up and then down by a small increment of 0.11 for every 2 years of simulation due to ease of implementation in the GCM. This gives a total simulation time of 58 years. Because of the step transition every 2 years, there is a small transient effect in the model state before settling back to a stationary state after approximately 200 d. To exclude any spurious effects in the early warning indicators, we calculate them only for the last year (360 d) of each step change in RoT.
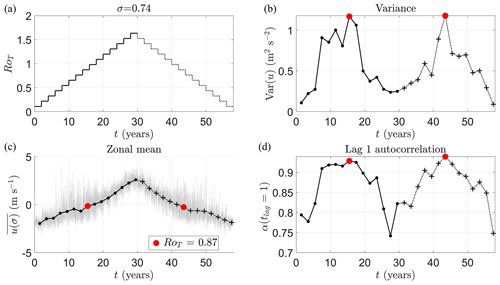
Figure 10Ramped control parameter runs with time. (a) Control parameter RoT value with simulation year. We start at RoT=0.11 and make stepped increases of 0.11 every 2 years to mimic a slow continuous change in the control parameter as closely as possible. We ramp up RoT to 1.64 over a period of 30 years (solid black line) before slowly ramping down back to 0.11 over the next 28 years (dotted black line). (c) Zonal mean wind speed u(σ,t) at σ=0.74 in the equatorial spherical segment with time (grey lines) and (black dots are the ramp-up values, black crosses are the ramp-down values) for the last year of each stepped change in RoT. (b) Variance of u(σ,t) in the last year of each stepped change in RoT. (d) Lag-1 autocorrelation α(tlag=1) of u(σ,t) in the last year of each stepped change in RoT.
Figure 10a shows how RoT varies with time. The solid black line indicates the ramp-up of RoT, while the dotted black line indicates the ramp-down of RoT. In Fig. 10c, u(σ,t) (grey line) in the equatorial band is plotted against time. The periods of increased variance and positive skewness are clearly visible between years 6–18 and 42–50 (also in Fig. 10b). Some of this large-amplitude response is a short transient effect from adjustment to the step change in RoT (although this quickly dies away); however, these periods of increased variance and skewness are also present in the static RoT simulations. Black dots (ramp-up) and black crosses (ramp-down) in Fig. 10c are in the last year of the step change, avoiding this transient effect. EWS variance and lag-1 autocorrelation are shown in Fig. 10b and d, respectively.
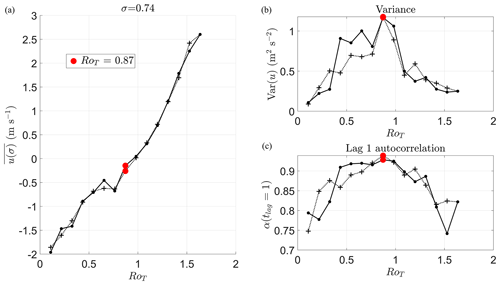
Figure 11Ramped control parameter runs as a function of RoT similar to Fig. 10 but with RoT as the x axis variable. (a) Mean zonal wind speed in the equatorial spherical segment for the last year of each stepped change in RoT. Black dots show values as RoT is ramped up (years 0–30), and black crosses show those values as RoT is ramped back down (years 30–58). (b) Variance of u(σ,t) in the last year of each stepped change in RoT. (c) Lag-1 autocorrelation α(tlag=1) of u(σ,t) in the last year of each stepped change in RoT. Black dots indicate values for the ramping up of RoT, while black crosses show RoT as it is ramping back down.
Although looks relatively symmetric around 30 years (the turning point of the control parameter), the EWSs do not. We plot these same quantities as a function of RoT in Fig. 11 to assess if there is any hysteresis when the control parameter is reversed and therefore whether bistability can be detected. In Fig. 11a we plot as it is ramping up (black dots) and ramping down (black crosses). Apart from a small region around the plateau in between RoT∼0.57–0.76, there does not appear to be any difference in the values of when ramping up and ramping down. In Fig. 11b and c EWS differences are larger; however, this is probably due to the short length of the time series used to calculate these statistical estimators and small transient effects. Also, as the standard error in the statistical estimators for a fixed sample size grows as autocorrelation increases, estimation should be worse in regions of large autocorrelation. Such a region exists for RoT∈[0.4 1.2], and this is where we find the largest discrepancies. Therefore, we do not expect the small differences to be statistically significant.
Unlike Suarez and Duffy (1992), we find no evidence of bistability in the mean equatorial zonal wind speed. However, our control parameter is markedly different from theirs. This, however, does not completely rule out bistability. There may be smaller regions of RoT that these simulations have not been able to resolve.
Although we have not found direct evidence of bistability, there is some evidence for flickering. In a system with multiple basins of attraction and noisy perturbations sufficiently strong to kick the system between these basins, a system may flicker between the attractors (Dakos et al., 2013). Flickering between multiple states can show up as asymmetry in the probability distribution of the system state variable. This asymmetry can be measured by the skewness. As previously mentioned, there are clearly visible periods of increased variance and positive skewness in δu(σ,t) between years 6–18 and 42–50 (RoT∼0.5 and RoT∼1.2) in Fig. 10c. We plot skewness with RoT at vertical height σ=0.74 in Fig. 12c (solid black line). Skewness peaks at RoT=0.44 during the ramp-up and RoT=0.55 during the ramp-down, although there is high positive skewness (Skew (u)>0.5) for . This peak in skewness occurs just before the oscillations start, although high positive skewness is present throughout the existence of the oscillations. We have also looked at how skewness changes with vertical height. Positive skewness peaks at σ=0.74, which is the level of the final transition. Negative skewness peaks at σ∼0.2 (dotted line in Fig. 12b), which is the vertical height where the first transition occurs. At σ=0.19 a similar graph of skewness with RoT is found to that of σ=0.74; however, positive skewness values are mapped to negative values. Little skewness is found around σ∼0.3 (dashed–dotted line); this is roughly the height of the top of the Hadley cells. This may indicate the presence of multiple states in the range . This is also approximately the range where the ramp-up and ramp-down values differ. The flickering states seem to be the oscillating Hadley cell state (typical of the final transition) and the superrotating upper troposphere state (typical of the first transition).
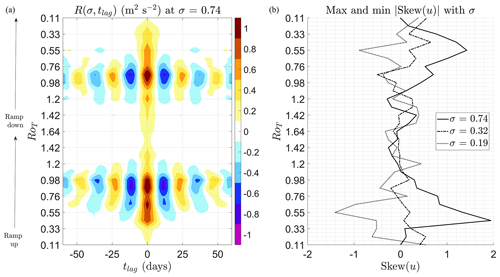
Figure 12Ramped control parameter R(σ,tlag) at vertical height σ=0.74 and skewness for δu(σ,t) at vertical heights σ=0.74 (largest positive skewness, final transition vertical height), σ=0.32 (smallest absolute skewness values, height of top of Hadley cells) and σ=0.19 (largest negative skewness values, first transition vertical height). The ramp-up starts from the bottom of the y axis, and the ramp-down starts from RoT=1.64 and continues up the y axis. (a) Although there are some small differences in ramp-up and ramp-down values, these are minor, and oscillations in R(σ,tlag) appear in roughly the same place with the same amplitude and period. (b) High positive skewness (>0.5) and high negative skewness are present in δu(σ,t) for at vertical heights of σ=0.74 and σ=0.19, respectively. This could indicate the presence of flickering, i.e. noise-induced transitions between attractors.
The oscillations in the fluctuations, δu(σ,t), around the mean zonal u(σ,t) in the equatorial band around the final transition suggest the minimal approximate description of the dynamics must be at a second-order or higher level. Motivated by this and the interesting structure in the variance and autocovariance, we next use a method to diagnose any higher-order dynamics of the fluctuations in the full global horizontal wind field . We look at the dominant spatial vector modes of δv and their stability at vertical height σ.
In Sect. 4, the state parameter x(t) was a real-valued scalar, and the theory developed to investigate the stability of a stationary state, , to small perturbations, δx(t), assumed first-order dynamics. We remove the restriction on scalar x and therefore make higher-order dynamics possible to describe and diagnose here. This is done by upgrading δx(t) to δx(t), an N component vector (vectors are denoted by bold type face). The technique we next describe goes by several names, such as principal oscillation pattern (POP) analysis (Hasselmann, 1988; von Storch and Zwiers, 1999), linear inverse modelling (LIM) (Penland, 1989) or empirical normal mode (ENM) analysis (Penland and Ghil, 1993; Brunet, 1994). Amongst others, this approach has been used to study the El Niño–Southern Oscillation (Penland and Magorian, 1993) and midlatitude jets (Farrell and Ioannou, 1995). The technique we use here approximates a (typically) non-linear dynamical system with a reduced number of linear modes. However, there are approaches that remove this linear approximation. One such example is the reconstruction of the Koopman operator (e.g. Budišić et al., 2012).
We can repeat the steps in Sect. 4 for the vector generalisation (see Williamson and Lenton, 2015, and Appendix A for details). We again want to study the response of small fluctuations δx(t) around some mean state to assess the stability of that mean state. As the state becomes less stable approaching the transition, fluctuations become larger and longer lived. Analogously to the scalar case, the dynamics of the fluctuations are determined by the Jacobian J(x); however, this is now a N×N matrix. J(x) can be decomposed into N modes (the eigenvectors of J) associated with N timescales (the eigenvalues of J), the largest of which will dominate the dynamics of the fluctuations. The early warning signals, i.e. autocorrelation and variance, are still functions of J(x) in the vector setting, but they are now also matrices (autocovariance and covariance matrices, respectively). We will analyse the properties of J in the following as this is what ultimately determines stability (and the EWSs, which are functions of J).
We identify the vector δx(t) at each time t in Eq. (A1) to have components δxi(t) that are the at each horizontal grid box labelled i in the GCM with coordinates (θi,ϕi) at vertical level σ. This two-dimensional horizontal field is area-weighted by grid box size, reshaped into a column vector and concatenated with the analogous field of . Time is also a discrete variable in the GCM output and has integer day values with the following interval: Δt=1 d. We label the full vector as δvt.
As the full-resolution horizontal field in this configuration of Isca has grid boxes for each field of u and v, the vector has 16 384 components. The resulting reconstructed J would therefore be a real-valued result, but it would be a non-symmetric 16 384×16 384 matrix, and calculating this matrix would be computationally costly. To reduce this cost, we project fields of δu and δv at each time t onto their n largest empirical orthogonal functions (EOFs), the dominant eigenvectors of the covariance matrix Σ, to capture the dominant dynamics of δv(t) (see von Storch and Zwiers, 1999, for a description of the EOF technique). We use n=60, which captures between 76 % and 88 % of the total variance depending on the value of RoT and σ. We have experimented with using larger n, and while more of the total variance is captured, the results presented below remain invariant. This is because we are interested in the dominant modes of the dynamics (largest eigenmodes of J), and these are captured well by the projections on to the leading EOFs.
Using the reduced EOF basis for δvt, we calculate A and Σ (see Appendix A) using the last 2 years of each RoT simulation and therefore infer J using Eqs. (A21) and (A22) for the full global horizontal vector wind field fluctuations.
6.1 Final transition: RoT∼0.87 at σ=0.74
We now apply the vector technique described in Appendix A to the full spatial horizontal vector wind field at vertical height σ=0.74 and diagnose the dominant eigenvalues and eigenmodes as RoT is varied through the final superrotation transition. Performing an eigendecomposition to find the dominant modes and their stabilities on each reconstructed J results in Fig. 13 for the final transition.
At vertical height σ=0.74, we show that one particular eigenmode, referred to as the “precursor” mode (Fig. 13b and red lines in the middle column of Fig. 13), is responsible for early warnings of the final transition. The precursor mode is an oscillating mode with a zonal wavenumber of 0 and a 25 d period. It becomes important in the dynamics just before the final transition, dominates the dynamics at the final transition and decays quickly following the final transition. We can therefore categorise the precursor mode as a spatial signature heralding the final transition in addition to the usual widely used temporal EWSs. This mode is correlated to oscillations in the equatorial meridional overturning strength (the Hadley cells) seen in Sect. 4.1.3.
After the final transition, the eigenmode referred to as the “superrotation” mode (Fig. 13c and blue lines in the middle column of Fig. 13) dominates the fluctuation dynamics. This is has a zonal wavenumber of 1 and propagates eastward (Fig. 14b) with a period of ∼4 d. The spatial pattern of this mode appears very similar to the Kelvin–Rossby instability that others have previously identified (Mitchell and Vallis, 2010; Wang and Mitchell, 2014; Zurita-Gotor and Held, 2018; Zurita-Gotor et al., 2022). In this mechanism, off-equatorial Rossby waves (diagonal lobes in Figs. 13c and 14b) centred around ±40° latitude couple with an equatorial Kelvin wave (equatorial lobe in the same figures) to converge momentum onto the Equator and enable superrotation.
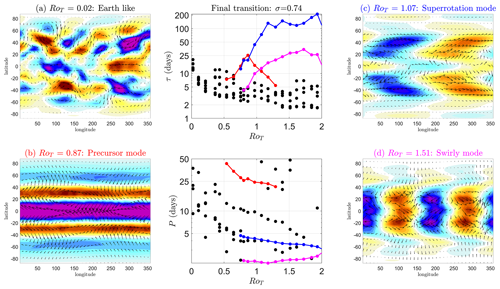
Figure 13Spatial precursors of the final superrotation transition at vertical height σ=0.74. The seven leading eigenvalues of the Jacobian of the global horizontal wind field fluctuations (δv(t)) around the mean state as RoT changes. The real part of the eigenvalues, determining the stability and the dominance in the dynamics of the associated mode, are shown in the upper-middle panel as a timescale . The corresponding imaginary part of the eigenvalues, determining the oscillation frequency of the associated mode, is shown as an oscillation period . Three of the largest eigenmodes are colour coded and tracked through different values of RoT to show how they evolve in the spectrum of J (middle column). In (c) and (d) the eigenmodes associated with the colour-coded eigenvalues are shown. Eigenmodes are dynamic but are shown at t=0 before they oscillate with period P and damping takes place (exponential decay with timescale τ). The filled coloured contours indicate the magnitude of the component of the mode (eigenmodes are dimensionless) with δu<0 (blue) and δu>0 (red) shown. Arrows show the full vector field . The modes are (a) Earth-like (black), (b) precursor (red), (c) superrotation (blue) and (d) swirly (magenta).
6.1.1 Eigenvalues of J: timescales and oscillation frequencies
The spectrum of each J (the first seven eigenvalues, λi , where ) as a function of RoT are shown in the middle column of Fig. 13. Generally each λi has a real and imaginary part. The real part, ℛ(λi), determines how dominant the associated eigenmode is in the dynamics, with less negative values being more dominant. Equivalently, the eigenmodes with the largest e-folding timescales, τi, dominate the dynamics (recall ). We choose to represent the real part of each eigenvalue as a timescale τi in the upper-middle panel of Fig. 13.
The imaginary part of each eigenvalue, ωi=ℐ(λi), determines the oscillation frequency of the associated eigenmode. We choose to represent the imaginary part of each eigenvalue as the period of the oscillation in the lower-middle panel of Fig. 13.
Each black dot represents one of the seven leading eigenvalues. At low values of RoT, the timescales of the leading modes are very close or the same (degenerate) within calculated error bounds from finite-sample-length tf−ts. This effective degeneracy in J can result in some non-uniqueness in the decomposed eigenmodes. In contrast, leading τi become well separated for RoT>0.36 (around the start of the oscillations where skewness peaks) and eigenmodes can be reliably inferred. We have highlighted how the τi of three leading eigenmodes around the transition change with RoT in the upper-middle panel and the associated oscillation periods Pi in the lower-middle panel Fig. 13. These are colour coded to the associated spatial mode: black is the Earth-like mode (Fig. 13a), red is the precursor mode (Fig. 13b), blue is the superrotation mode (Fig. 13c) and magenta is the “swirly” mode (Fig. 13d).
6.1.2 Eigenvectors of J: spatial mode structure
The leading modes of J, the eigenvectors associated with the eigenvalues with the largest τi around the final transition, are discussed next. These are dynamic modes that change with time according to Eq. (A10). We have tried to show the evolution of the precursor and superrotation mode through one full oscillation in Fig. 14 (animations of these modes are also available; see the “Video supplement”). These modes show how the vector wind field adjusts when perturbed from its mean state. An analogy would be the most visible pattern of a drum skin vibration (the dominant eigenmode) from rest (the mean state) when hit with a drumstick (the perturbation). Eigenvectors for a real-valued Jacobian are unique up to a global sign provided eigenvalues are non-degenerate, i.e. .
Earth-like mode. This spatial pattern can only be identified for RoT=0.02, which is an Earth-like simulation (black, Fig. 13a). Although it is the dominant mode, due to the close spacing of the τi at RoT=0.02, this pattern alone does not account for very much of the dynamics of δv. It has a timescale of τ∼20 d and an oscillation frequency of P∼20 d. This mode is like a jet stream, capturing the midlatitude instabilities.
Precursor mode. The precursor mode spatial pattern (red, Fig. 13b) appears at RoT∼0.5 and is the dominant mode in the fluctuation dynamics between RoT≈0.75 and RoT=0.87, although a second mode, the superrotation mode, is similar in size during this RoT interval. At RoT=0.87 the mode peaks in τ with a decay timescale of τ∼25 d, and this is when the early warning indicators of Sect. 4 all peak just before the transition. It is responsible for the shape of the variance of zonal mean u in Fig. 6 and the oscillating autocovariance function R(tlag) in the same figure as it is a zonal-wavenumber-0 mode with P∼25 d. This is why we refer to this mode as the precursor mode. After the peak, this mode then reduces quickly in importance until it is no longer detectable at RoT∼1.3. It is the third-largest mode from RoT>1. The evolution of this mode through one full cycle is shown in Fig. 14b. Physically, this appears to represent the fluctuations in the strength of mean meridional overturning circulation, particularly in fluctuations in the strength of the Hadley cells.
Superrotation mode. This mode alone clearly dominates the dynamics (largest τi) when the atmosphere becomes fully superrotating for RoT≥1 (blue, Fig. 13c). It is also an important component of the fluctuation dynamics around the transition at RoT∼0.75 when it is a similar size to the precursor mode. This is also when it first appears as a mode of J. We call this mode the superrotation mode. The e-folding timescale of this mode gets as large as τ∼200 d past RoT>1 and has an oscillation frequency of P∼4 d. It is a mode with a zonal wavenumber of 1. The evolution of this mode through one full cycle is shown in the second row of Fig. 14, and this shows that it is propagating eastward. This mode is has a similar pattern to the Kelvin–Rossby instability identified by Mitchell and Vallis (2010) and others for a fully superrotating state, meaning that this is where an equatorial Kelvin wave (the equatorial lobe) couples with off-equatorial Rossby waves (the chevron-like lobes) that mutually amplify each other and converge zonal momentum on to the Equator.
Swirly mode. This mode is significant in the fluctuation dynamics after the superrotation transition (magenta, Fig. 13d), particularly for larger values of RoT, although it is never the dominant mode. It is a mode with a zonal wavenumber of 2 and oscillation frequency P∼2 d. We call this mode the swirly mode.
The start of the plateau in in Fig. 6 coincides with the appearance of the precursor mode, and the plateau ends with the appearance of the superrotation mode. One could argue the plateau in is also a precursor to the superrotation transition. However, it is the appearance of the precursor mode and its properties that produce the EWSs (rising variance, increasing α(tlag), R(tlag)) and heralds the transition to superrotation.
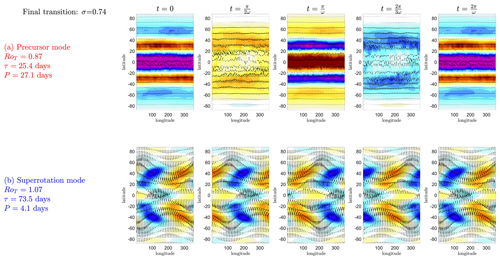
Figure 14Dynamic evolution of the eigenmodes of J at vertical height σ=0.74. As the eigenmodes of change with time according to Eq. (A10), we have tried to show this evolution through one full oscillation (please see the Video supplement for more information) of two of the dominant modes in Fig. 13. The filled colour indicates the component of the mode (eigenmodes are dimensionless) with δu<0 (blue) and δu>0 (red) shown. Arrows show the full vector field . The columns show the mode at the start of the cycle (t=0) and advance by a quarter of a cycle left to right. The rows of the figure show the modes: (a) precursor (red) and (b) superrotation (blue).
6.2 First transition: RoT∼0.07 at σ∼0.2
We next look at the eigenmodes around the first transition to superrotation at vertical height σ∼0.2. This first transition occurs near the tropopause. Because of the long timescales near the tropopause, we have run 10-year simulations and calculated J for the last 9 years of the simulation to help resolve the distinct modes (Fig. 15).
The first transition to superrotation occurs at vertical height σ∼0.2 at RoT∼0.07, and here we find a zonal-wavenumber-1 pattern very similar to the superrotation mode developing prior to the transition and dominating the dynamics. It is a long-period (P∼50–100 d) travelling mode; however, it is propagating westward rather than eastward (Fig. 15a). This mode propagates westward, increasing in period until at the transition the mode becomes effectively a standing mode (P→∞), at least up to the temporal resolution the simulations are able to resolve. It then becomes a long-period travelling-wave pattern again around RoT∼0.09 but now propagates eastward like the superrotation mode following the final transition.
Around the point of the first transition, the westward-propagating superrotation mode is replaced by a standing zonal-wavenumber-0 mode as the largest mode of J (Fig. 15b), rapidly dominating the dynamics with relatively large τ (green mode and line in Fig. 15). This remains the dominant mode until at least RoT=0.14.
It is harder to resolve modes well at vertical heights above σ<0.22 due to the increased timescales. Even at σ=0.22 and with 9 years of daily data to reconstruct J, only the “standing” mode (green mode) has a sizeable gap in between eigenvalues to resolve the mode well.
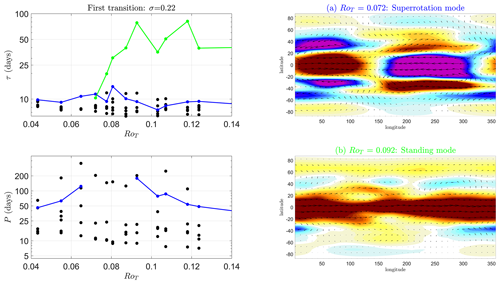
Figure 15Spatial precursors of the first superrotation transition at vertical height σ=0.22. The seven leading eigenvalues of the Jacobian of the global horizontal wind field fluctuations (δv(t)) around the mean state as RoT changes. The real part of the eigenvalues, determining the stability and the dominance in the dynamics of the associated mode, are shown in the left-hand upper panel as a timescale . The corresponding imaginary part of the eigenvalues, determining the oscillation frequency of the associated mode, is shown as an oscillation period . The two largest eigenmodes are colour coded and tracked through different values of RoT to show how they evolve in the spectrum of J (left column). In the right column we show the eigenmodes associated with the colour-coded eigenvalues. The zonal-wavenumber-1 superrotation eigenmode (blue) (a) is dynamic over a range of RoT but is shown at t=0 before it oscillates with period P and damping takes place (exponential decay with timescale τ). The zonal-wavenumber-0 standing mode (green) is a standing wave pattern (P→∞) and dominates the spectrum of J as the vertical level becomes superrotating. The filled coloured contours indicate the magnitude of the component of the mode (eigenmodes are dimensionless) with δu<0 (blue) and δu>0 (red) shown. Arrows show the full vector field . The modes are (a) the superrotation mode (blue) and (b) the standing mode (green).
6.3 Full vertical structure
The leading eigenmode structure follows a typical sequence, like those displayed in Figs. 16 and 17, at vertical heights between the first transition (σ∼0.2) and the final transition (σ=0.74). We have chosen vertical height σ=0.66 to show this typical sequence. This height is above the boundary layer and thus does not experience Rayleigh damping. The transition to superrotation at this vertical height occurs at RoT∼0.36.
The sequence of leading eigenmode from low to high RoT is as follows. A zonal-wavenumber-1 pattern similar to the superrotation mode (blue in Figs. 16 and 17) develops just before the local transition to superrotation at that particular vertical level. This eigenmode is then replaced by a zonal-wavenumber-0 standing mode pattern (green) at the transition to superrotation at that particular vertical level. As RoT is further increased, the precursor mode dominates until the final transition before the zonal-wavenumber-1 superrotation mode finally comes back and dominates the fluctuation dynamics following the final transition.
Generically, the local transition to superrotation at a particular vertical level is preceded by a long-period zonal-wavenumber-1 superrotation mode that is replaced at the transition by a standing zonal-wavenumber-0 mode. The final transition to superrotation, however, is preceded by the precursor mode.
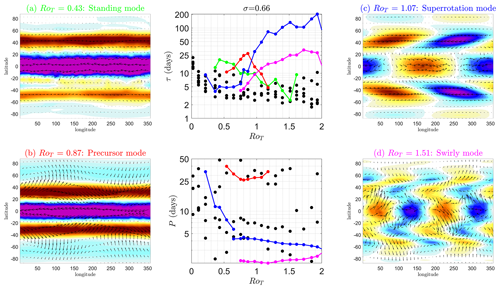
Figure 16Eigenmodes of J at vertical height σ=0.66. The seven leading eigenvalues of the Jacobian of the global horizontal wind field fluctuations, δv(t), around the mean state as RoT changes. The three largest eigenmodes are colour coded and tracked through different values of RoT to show how they evolve in the spectrum of J (middle column). In (c) and (d) we show the eigenmodes associated with the colour-coded eigenvalues. The zonal-wavenumber-0 standing eigenmode (a) dominates the dynamics just after the vertical level σ=0.66 becomes superrotating at RoT∼0.36. The precursor mode (b) takes over as the 25 d oscillations become more prevalent (RoT>0.5). Following the final transition at RoT>0.87, the superrotation mode (c) dominates the dynamics. The filled coloured contours indicate the magnitude of the component of the mode (eigenmodes are dimensionless) with δu<0 (blue) and δu>0 (red) shown. Arrows show the full vector field .
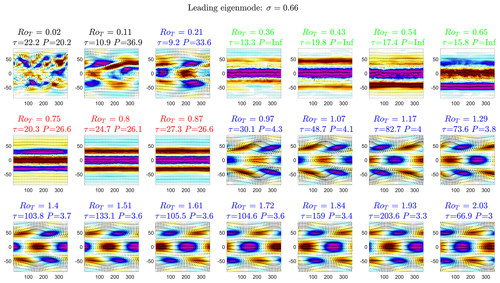
Figure 17Leading eigenmodes of J at vertical height σ=0.66 as RoT is varied. The e-folding timescale of the mode and period is given in each subtitle in units of days. Subtitles are colour coded by the representative mode. The superrotation-like zonal-wavenumber-1 mode (blue) first appears as the leading eigenmode at RoT=0.21. It is an eastward-propagating mode at this RoT and vertical level. This is replaced by the standing mode (green), a mode with a zonal wavenumber of 0 and infinite period, as this vertical level becomes superrotating. This is then replaced by another zonal-wavenumber-0 mode, the precursor mode (red), as the leading mode at RoT=0.75. This is a previously identified mode with period of P∼25 d. This is then replaced by the superrotation mode (blue) again at RoT≥0.97, which is also eastward propagating.
The motivation for this study came from Isaac Held's excellent blog (Held, 2016). One of the posts on that blog introduced the work of Suarez and Duffy (1992), who observed an abrupt transition to a superrotating state in an idealised two-vertical-level GCM as a longitude-dependent heat source in the tropics was increased. The atmospheric state in this model also showed bistability, i.e. both superrotating and regular, and present-day atmospheric states were stable for the same value of tropical heating. This example has many similarities with other climate tipping points (Lenton et al., 2019) – abrupt changes in state caused by relatively small changes in forcing parameters. These are generally regarded as low-probability, high-risk events. One such example is the Atlantic meridional overturning circulation (AMOC), which can abruptly change from an on state to an off state as freshwater flux into the North Atlantic is increased (Stommel, 1961; Vellinga and Wood, 2002; Mecking et al., 2016). The AMOC can also show bistability. The off state can persist as the freshwater flux is decreased back below the original threshold. There are a variety of other widely studied climate tipping points (e.g. the Amazon rainforest, Greenland ice sheet and Arctic sea ice); however, superrotation has not received the same attention. One of the motivations of this work was to begin to correct this deficiency.
Unlike Suarez and Duffy (1992), where the control parameter varied (the tropical heating) is arguably relevant to future anthropogenic climate change, our control parameter, the thermal Rossby number (RoT), a non-dimensional number that controls the global atmospheric dynamics, is probably not relevant to future climate change. Unlike the abrupt transition in equatorial mean zonal observed in Suarez and Duffy (1992), our transition is smooth as the control parameter is varied. The third difference is that we have not been able to detect bistability (Sect. 5), although evidence of noise-induced transitions between multiple states (flickering) was found within a subset of the control parameter range.
Although the thermal Rossby number is not likely to change very much as the climate warms, the mechanism for the transition may well be relevant, namely the Kelvin–Rossby instability. By changing the latitude of the baroclinic instability forcing, Zurita-Gotor et al. (2022) found that an abrupt transition to superrotation could be achieved via the Kelvin–Rossby instability mechanism. They also postulated this mechanism might be relevant for the transition found in warm climates by Caballero and Huber (2010). The simulations reported here do show early warnings of this transition and therefore serve as a test bed for the second motivation of this paper, namely whether we can detect this transition before it happens.
In the simulations reported here, the first transition to superrotation occurs just below the tropopause at vertical height σ∼0.2 and RoT∼0.07. As RoT increases, this superrotating region expands horizontally into the tropics, vertically up into the stratosphere and downwards into the troposphere. The superrotating region finally terminates at σ=0.83 at RoT=0.87 and does not extend any further, at least for values up to RoT=11.4. We term the transition of the lowest vertical level to superrotation at σ=0.74 as the final transition. We therefore do not see surface superrotation in these simulations, although this is known to occur in small regions of parameter space (Caballero and Carlson, 2018).
The usual early warnings of local bifurcation type tipping (rising variance and autocorrelation, Sect. 4) all increase before the both the first and final superrotation transition, indicative of critical slowing down near a local bifurcation. These EWSs are harder to detect near the tropopause around the first transition due to the difficulty resolving the differences between the long timescales that are naturally present in this part of the atmosphere.
In addition, the full autocovariance function, R(tlag), showed oscillations of a period of P∼25 d that became increasingly less damped as the final transition was approached, reminiscent of a Hopf type bifurcation (see Eq. 16). In a Hopf bifurcation, a pair of complex conjugate eigenvalues of the Jacobian move in the complex plane from the negative real half and cross the imaginary axis at the point of bifurcation (see Strogatz, 2001, for details). Before the bifurcation, this results in critical slowing down of the dynamics (increasingly less negative ℛ(λ)) and oscillations of frequency ω=ℐ(λ). These are observed in the superrotation transition. These oscillations are not present all the way through the troposphere. They exist for σ>0.3 and peak at σ∼0.45. These oscillations were correlated with oscillations in the strength of the Hadley cells. Both Northern Hemisphere and Southern Hemisphere cells simultaneously increase and decrease in strength as δu(σ,t) decreases and increases in strength, respectively.
In Thompson et al. (1994), the authors classify all codimension-1 bifurcations via observations from a slow control parameter sweep in a series of tables. Using this classification, our observations of a smooth transition, a Hopf-like autocorrelation function and lack of hysteresis point to a local supercritical Hopf bifurcation being present at the transition when the control parameter is the thermal Rossby number.
The presence of oscillations in δu motivated us to use a more general technique to study the transitions. The usual theory of EWSs relies on scalar state variables and first-order dynamics. This does not permit oscillations or higher-order dynamics. We gave a pedagogical introduction to the more general theory based on POP analysis in Appendix A and calculated the Jacobian and normal modes for the full global vector wind field . EWSs are designed to detect changes in the stability of the mean state and therefore must be functions of the Jacobian's eigenvalues that entirely describe the linear stability of the mean state. We therefore chose to study the eigenvalues and eigenmodes of the Jacobian as they are the sole determinant of traditional EWSs based on linear stability analysis.
When a system approaches a transition resulting from a local bifurcation, often a single eigenmode of the Jacobian starts to dominate the dynamics. Close to the final transition, we found two eigenmodes (or spatial patterns) that the fluctuations, δv, preferentially oscillate in before slowly decaying back towards the mean state . One of these modes, the precursor mode, was a zonal-wavenumber-0 mode that we attribute to the 25 d oscillations in the equatorial zonal mean δu and the rise in variance and autocorrelation seen in Sect. 4. There is also a second mode of roughly the same size around the final transition – the superrotation mode – a zonal-wavenumber-1 mode that comes to dominate the dynamics as the majority of the troposphere became fully superrotating. This is an eastward-propagating mode of a roughly 4 d period that looks very similar to the coupled Kelvin–Rossby mode identified by others.
Detecting the signature of the precursor mode in the spatial or temporal correlations would serve as the best EWS of the final transition. These modes were calculated for the global wind field. It is plausible that the precursor mode would be even more significant in the dynamics of the tropics if the spatial analysis was performed over just the tropical region rather than the entire globe. The attribution of a spatial signature as an early warning signal is something that has not been reported before, as far as we are aware, for a climate tipping point.
Just before the first transition, a zonal-wavenumber-1 mode very much like the superrotation mode appears, although it is propagating very slowly westward rather than eastward. At the first transition, this is replaced by a standing zonal-wavenumber-0 mode. As RoT increases, at vertical heights σ>0.3 this mode is replaced by the oscillating precursor mode, which peaks at the final transition at RoT=0.87 before the superrotation mode returns and dominates for RoT>0.87. Generically it appears the local transition to superrotation at a particular vertical level is preceded by a long-period zonal-wavenumber-1 superrotation mode that is replaced at the transition by a standing zonal-wavenumber-0 mode.
One may wonder why oscillations are not observed for RoT>1.3 after the precursor mode disappears from the dynamics in the scalar EWSs even though the dominant modes in this regime, the superrotation mode and the swirly mode, are oscillatory with periods of P∼4 and P∼2 d, respectively. This is due to their zonal wavenumbers. Remember that equatorial zonal u was averaged over a latitude band in Sect. 4. For non-zero zonal wavenumbers, the average will be always be zero, as there are an equal number of peaks and troughs. A zonal-wavenumber-0 pattern like the precursor mode. however, will have a non-zero average in a zonal mean.
There are still questions about the dynamical mechanisms giving rise to the observed eigenmodes around the transition. There are a lot of interesting dynamics going on. The superrotation mode appears to be the Kelvin–Rossby instability previously identified and studied by others (i.e. Williams, 2003; Wang and Mitchell, 2014; Mitchell and Vallis, 2010; Zurita-Gotor and Held, 2018; Zurita-Gotor et al., 2022). In this mechanism, superrotation arises from the wave–mean-flow interaction, specifically the interaction of equatorial Kelvin and off-equatorial Rossby waves that mutually amplify each other and generate a planetary-scale mode that converges zonal momentum onto the Equator. The global 25 d oscillations present around the transition are correlated to the strength of the Hadley cell intensity and are present up until the top of the meridional overturning cells. The banded zonal-wavenumber-0 structure also seems to hint that this mode represents the meridional overturning dynamics. It is also known that conventional Hadley cells with uplift at the Equator flux momentum out of this equatorial region and therefore should reduce the magnitude of superrotation based on how strong these cells are (which is observed here). These are hints at the underlying dynamics and details that have been left to a future study.
The degree of spatial correlation in the fluctuations, particularly in the precursor mode, is reminiscent of a phase transition (Anderson, 1984). Traditionally, phase transitions are studied via the statistics of the spatial fluctuations around the mean state. The hallmarks of a phase transition are diverging correlation length and correlation time (resulting in critical slowing down) and an abrupt change in the order parameter of the state. In particular, continuous phase transitions have spatial correlation functions that are described by a power law at the critical point giving rise to scale-invariant physics and often involve a broken symmetry. What are the similarities with the transition to superrotation? Diverging correlation time is present (τ), and diverging correlation length is qualitatively present (as seen in the pattern of the precursor mode, at least zonally), although we have not formally calculated spatial correlation functions. However, Dylewsky has found quantitative evidence via a neural network trained on the spatial information from a 2D Ising model phase transition. This trained neural network clearly predicts the superrotation transition before it occurs (Daniel Dylewsky, personal communication, 2023; see also Dylewsky et al., 2023).
Although the probability of transitioning to an equatorial surface superrotating atmospheric state under future climate change seems unlikely (Caballero and Carlson, 2018), it is not zero (see Held, 2016). There is (limited) evidence that it has happened in the past and can happen in the future (Huang et al., 2001; Caballero and Huber, 2010; Tziperman and Farrell, 2009). As with other tipping points, this makes superrotation a low-probability but high-risk event. Even though a surface superrotating atmospheric state seems unlikely, superrotation happens readily in the upper troposphere under high-end global warming scenarios. However, the impact on surface climate would probably be less severe (Caballero and Carlson, 2018). It would be interesting to repeat the experiment of Suarez and Duffy (1992) with the Isca framework, which would show a more relevant way of transitioning to superrotation under climate change, and see if the EWSs identified here are still present.
We can repeat the steps in Sect. 4 for the vector generalisation (see Williamson and Lenton, 2015, for further details). We again want to study the response of small fluctuations δx(t) around some mean state to assess the stability of that mean state. As the state becomes less stable approaching the transition, fluctuations become larger and longer lived. The state of the system in analogy to Eq. (9) is
The N components of the vector x(t) can be written explicitly as
Similar expressions can be written for δx and . The superscript T denotes the matrix transpose operator. The individual scalar components of x(t) are indexed with i, which can take the values . Each of the xi values is assumed to evolve autonomously, each according to a different and generally non-linear function fi(x). Note that each fi has the multi-variable input x. This means that fi is a function of all in general, meaning that each xi value is coupled, possibly non-linearly. Formally, each xi evolves according to . Provided the fluctuations are not too large, the dynamics are approximated well by making a multi-variable Taylor expansion of each fi(x) to the first order around the mean state, i.e. , where instead of a single number describing the stability of the system, the Jacobian is now an N×N matrix encoding the linear coupling between the components of x. The element in the ith row and jth column of J is given by . The dynamics of the fluctuations can be now be approximated with a linear first-order ODE; however, it is now a matrix equation
Analogous to the scalar x case, for a time-invariant mean state (and time-invariant J(x)), Eq. (A3) has the solution
J(x) still determines the behaviour and fate of small perturbations from and therefore 's stability. However, J(x) is a more complicated and general object than the single number of Sect. 4 due to the couplings between the various δxi (non-zero off-diagonal entries of J). One can uncouple the dynamics into N uncoupled modes, , by transforming each of the δxi values into a new basis (denoted by a tilde) that is a linear combination of the old δxi, i.e.
where represents scalar (and possibly complex) coefficients. These new values are vectors, although they behave like scalars and evolve independently of each other. Therefore, one can treat the dynamics as N scalar (although generally complex, rather than real valued) first-order ODEs like the one in Eq. (10). The problem of finding this new uncoupled basis, where the off-diagonal entries of J are zero, is equivalent to finding the eigendecomposition of the Jacobian
where is a diagonal matrix (only non-zero entries are on the diagonal) with N eigenvalues, each labelled by λi on the diagonal of associated with the N eigenvectors of J, denoted qj, given by the jth column of matrix Q. The same Q also diagonalises the matrix . Thus, the new basis in Eq. (A5) is simply given by , where gives the coefficients to uncouple the equations. The new basis given by the set of is the eigenmode, but these also go by other names; i.e. they are often known as linear, critical or normal modes.
How each of the evolve now reduces to the N equation
and therefore again there are three possible fates of an initial perturbation of amplitude on mode i depending on the sign of the real part of each of the λi. (i) The real part of λi is negative (ℛ(λi)<0), where the initial fluctuation in the normal mode decays, and this particular mode will be stable to perturbations. In this case a recovery time for this mode can be defined as . (ii) The real part of λi is positive (ℛ(λi)>0), where any initial fluctuation in this mode will get exponentially larger with time, and this mode will be unstable. (iii) The real part of λi is zero, i.e. ℛ(λi)→0. In this case, perturbations will not grow or decay in this mode. This neutral stability occurs at a bifurcation.
The evolution of the fluctuations around the mean of the entire system is described by a linear superposition of all N modes, i.e.
Therefore, all N modes must be stable for the overall system to be stable. If one or more of the modes are unstable, as time increases the unstable mode with the most positive real part will swamp the response of the other N−1 modes and cause the entire system to be unstable. This means that for a stable system the requirement must be ℛ(λi)≤0 ∀i. Provided all the modes are stable, the with the least negative ℛ(λi) will dominate the dynamics of the system simply because they decay more slowly (larger τi) than those modes associated with shorter τi (more negative ℛ(λi)). This means that the dynamics of the entire system may be described well by just a few (n) modes, where n<N, with the largest timescales such that
where λi values are ordered in increasing size, i.e. . An extreme example is when a local bifurcation is approached and the timescale of one (or more) of the modes is τi→∞ (ℛ(λi)→0) and dominates the dynamics to such a degree that the system can be described by just that one (or more) mode.
The eigenvalues λi can also have imaginary components. These give rise to oscillations in the associated mode with angular frequency ωi=ℐ(λi). For a real-valued J, complex λi values always occur in complex conjugate pairs with associated complex conjugate eigenvectors. If eigenvalues (and therefore eigenvectors) are complex, the superposition with its conjugate mode gives a real but time-evolving spatial mode. Explicitly, for a single dominant complex (oscillatory) mode (ℛ(λ1)≫ℛ(λi), ), the dynamics are
This means that the mode spatially oscillates between its real and imaginary parts at angular frequency ω1. In the last line, we define the following vector phase: .
For a dominant real mode, the dynamics are
Since ω1=0 and , there is no conjugate mode. A mode associated with a real eigenvalue has real eigenmode, and therefore the spatial pattern remains fixed, decaying exponentially and uniformly from the constant multiplier on the pattern . This case is analogous with the first-order dynamics scalar case of Sect. 4, with the constant multiplier being the lag-1 autocorrelation and the spatial mode analogous to the scalar variable x.
One may wonder how Eq. (A3) describes higher-order dynamics since it is a first-order ODE. A Nth-order system can be written as a first-order vector ODE with N dimensions. For example, the third-order system
can be written as a first-order vector ODE in three dimensions by making the identifications and so that Eq. (A15) can be written
or as a first-order vector ODE
which can be written more compactly in the same form as Eq. (A3) as follows:
Under the assumption of white-noise forcing (or equivalently independent errors in δxi), one can reconstruct J from time series of the δxi, with each time series sampled at an interval Δt between time steps as follows (see Williamson and Lenton, 2015, for details)
where Σ is the covariance matrix of δx and A is the lagged covariance matrix:
One can then find the eigenmodes and eigenvalues of J (and hence their stability). For vector-valued x, the analogous EWSs to the scalar case (Sect. 4) are now matrix valued:
However, we now have N modes (eigenvectors of J) associated with N timescales (eigenvalues of J). The autocorrelation and variance of early warning signals are still functions of J(x), but they are now also matrices (autocovariance and covariance matrices, respectively). We analyse the properties of J in this paper as this is what ultimately determines stability (and the EWSs, which are functions of J).
Data and code used in this paper are available from the corresponding author.
Animations of the leading eigenmode evolution around the final transition (Fig. 14) are available at https://doi.org/10.5446/63009 (Williamson, 2024).
MSW carried out the data analysis and drafted the paper. All authors contributed to the submitted paper.
The contact author has declared that neither of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
This article is part of the special issue “Tipping points in the Anthropocene”. It is a result of the “Tipping Points: From Climate Crisis to Positive Transformation” international conference hosted by the Global Systems Institute (GSI) and University of Exeter (12–14 September 2022), as well as the associated creation of a Tipping Points Research Alliance by GSI and the Potsdam Institute for Climate Research, Exeter, Great Britain, 12–14 September 2022.
We would like to thank Isaac Held for introducing us to superrotation via his excellent blog, and we also grateful for the comments of four anonymous referees that substantially improved this paper.
This research has been supported by the EU H2020 European Research Council (grant nos. 742472 and 641816).
This paper was edited by Jesse F. Abrams and reviewed by four anonymous referees.
Anderson, W.: Basic Notions Of Condensed Matter Physics, Basic Books, CRC Press, https://doi.org/10.4324/9780429494116, 1984. a
Armstrong McKay, D. I., Staal, A., Abrams, J. F., Winkelmann, R., Sakschewski, B., Loriani, S., Fetzer, I., Cornell, S. E., Rockström, J., and Lenton, T. M.: Exceeding 1.5°C global warming could trigger multiple climate tipping points, Science, 377, eabn7950, https://doi.org/10.1126/science.abn7950, 2022. a
Arnold, N. P., Tziperman, E., and Farrell, B.: Abrupt Transition to Strong Superrotation Driven by Equatorial Wave Resonance in an Idealized GCM, J. Atmos. Sci., 69, 626–640, https://doi.org/10.1175/JAS-D-11-0136.1, 2012. a, b, c, d, e, f
Ashwin, P., Wieczorek, S., Vitolo, R., and Cox, P.: Tipping points in open systems: Bifurcation, noise-induced and rate-dependent examples in the climate system, Philos. T. Roy. Soc. A, 370, 1166–1184, 2012. a
Brovkin, V., Claussen, M., Petoukhov, V., and Ganopolski, A.: On the stability of the atmosphere-vegetation system in the Sahara/Sahel region, J. Geophys. Res.-Atmos., 103, 31613–31624, https://doi.org/10.1029/1998JD200006, 1998. a
Brunet, G.: Empirical Normal-Mode Analysis of Atmospheric Data, J. Atmos. Sci., 51, 932–952, https://doi.org/10.1175/1520-0469(1994)051<0932:ENMAOA>2.0.CO;2, 1994. a
Budišić, M., Mohr, R., and Mezić, I.: Applied Koopmanism, Chaos: An Interdisciplinary Journal of Nonlinear Science, 22, 047510, https://doi.org/10.1063/1.4772195, 2012. a
Bury, T. M., Bauch, C. T., and Anand, M.: Detecting and distinguishing tipping points using spectral early warning signals, J. R. Soc. Interface, 17, 20200482, https://doi.org/10.1098/rsif.2020.0482, 2020. a
Caballero, R. and Carlson, H.: Surface Superrotation, J. Atmos. Sci., 75, 3671–3689, https://doi.org/10.1175/JAS-D-18-0076.1, 2018. a, b, c, d, e, f, g
Caballero, R. and Huber, M.: Spontaneous transition to superrotation in warm climates simulated by CAM3, Geophys. Res. Lett., 37, L11701, https://doi.org/10.1029/2010GL043468, 2010. a, b, c, d, e
Dakos, V., Scheffer, M., van Nes, E. H., Brovkin, V., Petoukhov, V., and Held, H.: Slowing down as an early warning signal for abrupt climate change, P. Natl. Acad. Sci. USA, 105, 14308–14312, 2008. a
Dakos, V., van Nes, E. H., and Scheffer, M.: Flickering as an early warning signal, Theor. Ecol., 6, 309–317, https://doi.org/10.1007/s12080-013-0186-4, 2013. a, b
Ditlevsen, P. D. and Johnsen, S. J.: Tipping points: Early warnings and wishful thinking, Geophys. Res. Lett., 37, L19703, https://doi.org/10.1029/2010GL044486, 2010. a
Dylewsky, D., Lenton, T. M., Scheffer, M., Bury, T. M., Fletcher, C. G., Anand, M., and Bauch, C. T.: Universal early warning signals of phase transitions in climate systems, J. R. Soc. Interface, 20, 20220562, https://doi.org/10.1098/rsif.2022.0562, 2023. a
Farrell, B. F. and Ioannou, P. J.: Stochastic dynamics of the midlatitude atmospheric jet, J. Atmos. Sci., 52, 1642–1656, 1995. a
Feudel, U.: Rate-induced tipping in ecosystems and climate: the role of unstable states, basin boundaries and transient dynamics, Nonlin. Processes Geophys., 30, 481–502, https://doi.org/10.5194/npg-30-481-2023, 2023. a
Gierasch, P. J.: Meridional Circulation and the Maintenance of the Venus Atmospheric Rotation, J. Atmos. Sci., 32, 1038–1044, https://doi.org/10.1175/1520-0469(1975)032<1038:MCATMO>2.0.CO;2, 1975. a
Gordon, C. T. and Stern, W. F.: A Description of the GFDL Global Spectral Model, Mon. Weather Rev., 110, 625–644, https://doi.org/10.1175/1520-0493(1982)110<0625:ADOTGG>2.0.CO;2, 1982. a
Hasselmann, K.: PIPs and POPs: The reduction of complex dynamical systems using principal interaction and oscillation patterns, J. Geophys. Res.-Atmos., 93, 11015–11021, https://doi.org/10.1029/JD093iD09p11015, 1988. a
Held, H. and Kleinen, T.: Detection of climate system bifurcations by degenerate fingerprinting, Geophys. Res. Lett., 31, L23207, https://doi.org/10.1029/2004GL020972, 2004. a
Held, I. M.: Equatorial superrotation in Earth-like atmospheric models, https://www.gfdl.noaa.gov/wp-content/uploads/files/user_files/ih/lectures/super.pdf (last access: 25 November 2024), 1999. a
Held, I. M.: Superrotation, idealized models, and GCMs, https://www.gfdl.noaa.gov/blog_held/68-superrotation-idealized-models-and-gcms/#more-36652 (last acces: 27 July 2023), 2016. a, b, c
Held, I. M. and Suarez, M. J.: A Proposal for the Intercomparison of the Dynamical Cores of Atmospheric General Circulation Models, B. Am. Meteor. Soc., 75, 1825–1830, https://doi.org/10.1175/1520-0477(1994)075<1825:APFTIO>2.0.CO;2, 1994. a, b
Herbert, C., Caballero, R., and Bouchet, F.: Atmospheric Bistability and Abrupt Transitions to Superrotation: Wave-Jet Resonance and Hadley Cell Feedbacks, J. Atmos. Sci., 77, 31–49, https://doi.org/10.1175/JAS-D-19-0089.1, 2020. a
Hide, R.: Dynamics of the Atmospheres of the Major Planets with an Appendix on the Viscous Boundary Layer at the Rigid Bounding Surface of an Electrically-Conducting Rotating Fluid in the Presence of a Magnetic Field, J. Atmos. Sci., 26, 841–853, https://doi.org/10.1175/1520-0469(1969)026<0841:DOTAOT>2.0.CO;2, 1969. a
Huang, H.-P., Weickmann, K. M., and Hsu, C. J.: Trend in Atmospheric Angular Momentum in a Transient Climate Change Simulation with Greenhouse Gas and Aerosol Forcing, J. Climate, 14, 1525–1534, https://doi.org/10.1175/1520-0442(2001)014<1525:TIAAMI>2.0.CO;2, 2001. a, b, c
IPCC: The Ocean and Cryosphere in a Changing Climate: Special Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, https://doi.org/10.1017/9781009157964, 2019. a
IPCC: Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, https://doi.org/10.1017/9781009157896, 2023. a
Laraia, A. L. and Schneider, T.: Superrotation in Terrestrial Atmospheres, J. Atmos. Sci., 72, 4281–4296, https://doi.org/10.1175/JAS-D-15-0030.1, 2015. a
Lenton, T., Rockström, J., Gaffney, O., Rahmstorf, S., Richardson, K., Steffen, W., and Schellnhuber, H.: Climate tipping points – too risky to bet against, Nature, 575, 592–595, https://doi.org/10.1038/d41586-019-03595-0, 2019. a
Lenton, T. M.: Early warning of climate tipping points, Nat. Clim. Change, 1, 201–209, 2011. a, b
Lenton, T. M., Livina, V. N., Dakos, V., van Nes, E. H., and Scheffer, M.: Early warning of climate tipping points from critical slowing down: comparing methods to improve robustness, Philos. T. R. Soc. A, 370, 1185–1204, 2012. a
Livina, V. N. and Lenton, T. M.: A modified method for detecting incipient bifurcations in a dynamical system, Geophys. Res. Lett., 34, L03712, https://doi.org/10.1029/2006GL028672, 2007. a
Loriani, S., Aksenov, Y., Armstrong McKay, D., Bala, G., Born, A., Chiessi, C. M., Dijkstra, H., Donges, J. F., Drijfhout, S., England, M. H., Fedorov, A. V., Jackson, L., Kornhuber, K., Messori, G., Pausata, F., Rynders, S., Salée, J.-B., Sinha, B., Sherwood, S., Swingedouw, D., and Tharammal, T.: Tipping points in ocean and atmosphere circulations, EGUsphere [preprint], https://doi.org/10.5194/egusphere-2023-2589, 2023. a
Mecking, J. V., Drijfhout, S. S., Jackson, L. C., and Graham, T.: Stable AMOC off state in an eddy-permitting coupled climate model, Clim. Dynam., 47, 2455–2470, https://doi.org/10.1007/s00382-016-2975-0, 2016. a, b
Mitchell, J. L. and Vallis, G. K.: The transition to superrotation in terrestrial atmospheres, J. Geophys. Res.-Planets, 115, E12008, https://doi.org/10.1029/2010JE003587, 2010. a, b, c, d, e, f, g, h, i, j, k, l
Penland, C.: Random forcing and forecasting using principal oscillation pattern analysis, Mon. Weather Rev., 117, 2165–2185, https://doi.org/10.1175/1520-0493(1989)117<2165:RFAFUP>2.0.CO;2, 1989. a
Penland, C. and Ghil, M.: Forecasting Northern Hemisphere 700 mb geopotential height anomalies using empirical normal modes, Mon. Weather Rev., 121, 2355–2371, https://doi.org/10.1175/1520-0493(1993)121<2355:FNHMGH>2.0.CO;2, 1993. a
Penland, C. and Magorian, T.: Prediction of Niño 3 Sea Surface Temperatures Using Linear Inverse Modeling, J. Climate, 6, 1067–1076, http://www.jstor.org/stable/26197251, 1993. a
Pierrehumbert, R. T.: Climate change and the tropical Pacific: The sleeping dragon wakes, P. Natl. Acad. Sci. USA, 97, 1355–1358, https://doi.org/10.1073/pnas.97.4.1355, 2000. a, b
Read, P. L.: Super-rotation and diffusion of axial angular momentum: II. A review of quasi-axisymmetric models of planetary atmospheres, Q. J. Roy. Meteor. Soc., 112, 253–272, https://doi.org/10.1002/qj.49711247114, 1986. a
Read, P. L. and Lebonnois, S.: Superrotation on Venus, on Titan, and Elsewhere, Annu. Rev. Earth Planet. Sci., 46, 175–202, https://doi.org/10.1146/annurev-earth-082517-010137, 2018. a
Saravanan, R.: Equatorial Superrotation and Maintenance of the General Circulation in Two-Level Models, J. Atmos. Sci., 50, 1211–1227, https://doi.org/10.1175/1520-0469(1993)050<1211:ESAMOT>2.0.CO;2, 1993. a, b, c
Scheffer, M., Bacompte, J., Brock, W. A., Brovkin, V., Carpenter, S. R., Dakos, V., Held, H., van Nes, E. H., Rietkerk, M., and Sugihara, G.: Early warning signals for critical transitions, Nature, 461, 53–59, 2009. a
Scheffer, M., Carpenter, S. R., Lenton, T. M., Bascompte, J., Brock, W., Dakos, V., van de Koppel, J., van de Leemput, I. A., Levin, S. A., van Nes, E. H., Pascual, M., and Vandermeer, J.: Anticipating Critical Transitions, Science, 338, 344–348, 2012. a
Scott, R. K. and Polvani, L. M.: Equatorial superrotation in shallow atmospheres, Geophys. Res. Lett., 35, L24202, https://doi.org/10.1029/2008GL036060, 2008. a
Shell, K. M. and Held, I. M.: Abrupt Transition to Strong Superrotation in an Axisymmetric Model of the Upper Troposphere, J. Atmos. Sci., 61, 2928–2935, https://doi.org/10.1175/JAS-3312.1, 2004. a, b
Stommel, H.: Thermohaline convection with two stable regimes of flow, Tellus, 13, 224–230, 1961. a, b
Strogatz, S. H.: Nonlinear Dynamics and Chaos, Westview Press, https://doi.org/10.1201/9780429492563, 2001. a, b
Suarez, M. J. and Duffy, D. G.: Terrestrial Superrotation: A Bifurcation of the General Circulation, J. Atmos. Sci., 49, 1541–1554, https://doi.org/10.1175/1520-0469(1992)049<1541:TSABOT>2.0.CO;2, 1992. a, b, c, d, e, f, g, h, i, j, k, l, m, n
Tantet, A., van der Burgt, F. R., and Dijkstra, H. A.: An early warning indicator for atmospheric blocking events using transfer operators, Chaos, 25, 036406, https://doi.org/10.1063/1.4908174, 2015. a
Thompson, J. M. T. and Sieber, J.: Predicting climate tipping as a noisy bifurcation: A review, Int. J. Bif. Chaos, 21, 399–423, 2011. a
Thompson, J. M. T., Stewart, H. B., and Ueda, Y.: Safe, explosive, and dangerous bifurcations in dissipative dynamical systems, Phys. Rev. E, 49, 1019–1027, https://doi.org/10.1103/PhysRevE.49.1019, 1994. a
Tziperman, E. and Farrell, B.: Pliocene equatorial temperature: Lessons from atmospheric superrotation, Paleoceanography, 24, PA1101, https://doi.org/10.1029/2008PA001652, 2009. a, b, c
Vallis, G. K., Colyer, G., Geen, R., Gerber, E., Jucker, M., Maher, P., Paterson, A., Pietschnig, M., Penn, J., and Thomson, S. I.: Isca, v1.0: a framework for the global modelling of the atmospheres of Earth and other planets at varying levels of complexity, Geosci. Model Dev., 11, 843–859, https://doi.org/10.5194/gmd-11-843-2018, 2018. a
Vellinga, M. and Wood, R. A.: Global climatic impacts of a collapse of the Atlantic thermohaline circulation, Clim. Change, 54, 43–63, 2002. a, b
von Storch, H. and Zwiers, F. W.: Statistical Analysis in Climate Research, Cambridge University Press, https://doi.org/10.1017/CBO9780511612336, 1999. a, b, c
Wang, P. and Mitchell, J. L.: Planetary ageostrophic instability leads to superrotation, Geophys. Res. Lett., 41, 4118–4126, https://doi.org/10.1002/2014GL060345, 2014. a, b, c, d
Wieczorek, S., Ashwin, P., Luke, C. M., and Cox, P. M.: Excitability in ramped systems: The compost-bomb instability, P. R. Soc. A, 10, 1098, https://doi.org/10.1098/rspa.2010.0485, 2010. a
Wiesenfeld, K.: Noisy precursors of nonlinear instabilities, J. Stat. Phys., 38, 1071–1097, 1985. a
Williams, G. P.: Barotropic Instability and Equatorial Superrotation, J. Atmos. Sci., 60, 2136–2152, https://doi.org/10.1175/1520-0469(2003)060<2136:BIAES>2.0.CO;2, 2003. a, b
Williamson, M.: Dynamic evolution of eigenmodes of J, TIB AV-Portal [video], https://doi.org/10.5446/63009, 2024. a
Williamson, M. S. and Lenton, T. M.: Detection of bifurcations in noisy coupled systems from multiple time series, Chaos, 25, 036407, https://doi.org/10.1063/1.4908603, 2015. a, b, c
Zurita-Gotor, P. and Held, I. M.: The Finite-Amplitude Evolution of Mixed Kelvin–Rossby Wave Instability and Equatorial Superrotation in a Shallow-Water Model and an Idealized GCM, J. Atmos. Sci., 75, 2299–2316, https://doi.org/10.1175/JAS-D-17-0386.1, 2018. a, b, c, d
Zurita-Gotor, P., Anaya-Benlliure, A., and Held, I. M.: The Sensitivity of Superrotation to the Latitude of Baroclinic Forcing in a Terrestrial Dry Dynamical Core, J. Atmos. Sci., 79, 1311–1323, https://doi.org/10.1175/JAS-D-21-0269.1, 2022. a, b, c, d, e, f, g
- Abstract
- Introduction
- Methods
- Mean atmospheric state with varying RoT
- Temporal early warning signals
- Evidence of multiple states
- Spatial precursors to the superrotation transition
- Discussion and conclusion
- Appendix A: Vector-valued state parameter generalisation for early warnings of bifurcation-induced tipping
- Code and data availability
- Video supplement
- Author contributions
- Competing interests
- Disclaimer
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Methods
- Mean atmospheric state with varying RoT
- Temporal early warning signals
- Evidence of multiple states
- Spatial precursors to the superrotation transition
- Discussion and conclusion
- Appendix A: Vector-valued state parameter generalisation for early warnings of bifurcation-induced tipping
- Code and data availability
- Video supplement
- Author contributions
- Competing interests
- Disclaimer
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References