Absence of causality between seismic activity and global warming
There is no more consequential scientific matter today than global warming. The societal and policy implications, however, hinge upon the attribution of that warming to human activity and, specifically, continued societal reliance on the burning of fossil fuels. It was recently suggested that this warming could be explained by the non-anthropogenic factor of seismic activity. If that is the case, it would have profound implications. We have assessed the validity of the claim using a statistical technique (the method of conditional dispersion) that evaluates the existence of causal connections between variables, finding no evidence for any causal relationship between seismic activity and global warming.
The anthropogenic cause of planetary warming during the industrial era is well established (e.g., Stocker et al., 2014). This does not mean, however, that alternative hypotheses challenging an anthropogenic cause of observed warming should not be evaluated on their merit. Recently it was proposed that the warming (particularly in the polar regions) can be attributed to tectonic waves caused by large earthquakes and by the subsequent destruction of the microstructure of gas hydrates and release of the methane (Lobkovsky et al., 2022). To test this hypothesis, we apply the method of conditional dispersion (Čenys et al., 1991; Verbitsky et al., 2019) to explore a potential causal relationship between temperature and global seismic activity. The method has proven to be less noise-sensitive than convergent-cross-mapping algorithms and more universal than prediction-improvement approaches. Briefly, the method assumes that, if two variables are dependent (or in other words that the causality in Wiener's definition exists), then they belong to the same dynamical system. Therefore, if points of the first variable (e.g., the seismicity index) are close, the synchronous points of the second variable (e.g., the temperature) should also be close. Thus, the dependence of the conditional dispersion σ(ε) of the temperature variable upon the distance ε between synchronous points of the seismic-activity variable becomes a signature of a causal relationship between the temperature and the seismic activity. Specifically, if the seismic activity is the cause of the warming, then the conditional dispersion σ(ε) of the temperature variable should decrease when the distance ε between synchronous points of the seismic-activity variable decreases.
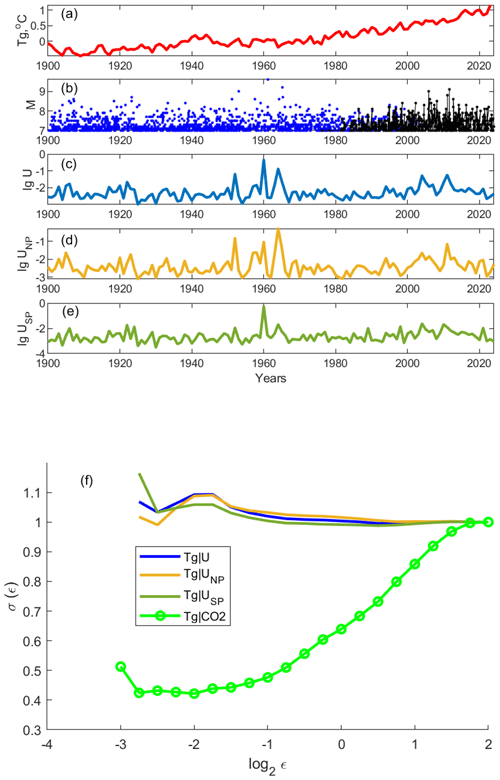
Figure 1(a) Global temperature anomaly data. (b) Earthquake magnitude data of Ammon et al. (2010) (dark blue), supplemented by the most recent fragment from the IRIS DMC database (https://ds.iris.edu/wilber3/find_event, last access: 22 July 2024) (black). (c) The seismicity index with only earthquake magnitudes M taken into account (blue). (d) The seismicity index where earthquake magnitudes M and the hypocentral distance R to the North Pole are accounted for (yellow). (e) The seismicity index where earthquake magnitudes M and the hypocentral distance R to the South Pole are accounted for (dark green). (f) Conditional dispersions of global temperature anomalies σ(ε), where ε is the distance between synchronous points of a seismicity index of a corresponding color and conditional dispersion of global temperature anomalies σ(ε), where ε is the distance between synchronous points of the atmospheric CO2 concentration (green circled line).
In Fig. 1 we present the results of the conditional dispersion calculations together with the data. Specifically, we use the earthquake magnitude data (Ammon et al., 2010) supplemented by the most recent fragment from the IRIS DMC database (https://ds.iris.edu/wilber3/find_event, last access: 22 July 2024). We defined the seismicity index as expected maximum values of crustal deformation, described by the empirical law of Okada (1995), i.e., , where Umax (cm) are expected maximum values of crustal deformation, M is earthquake magnitude, and R (km) is the hypocentral distance to the region of interest. Based on this law, we created three seismicity indexes: (a) in the first index, only the earthquake magnitude M is taken into account, and the hypocentral distance R is used only as a scaling constant; (b) in the second index, both the earthquake magnitude M and the hypocentral distance R to the North Pole are accounted for; and (c) the third index accounts for both the earthquake magnitude M and the hypocentral distance R to the South Pole. The Global Land-Ocean Temperature Index (Hansen et al., 2010; Lenssen et al., 2019, https://data.giss.nasa.gov/gistemp/, last access: 22 July 2024) has been used as the global temperature data Tg.
It can be seen that, for all three seismicity indexes, the conditional dispersion of global temperature anomalies σ(ε) is independent of ε, where ε is the distance between synchronous points of a seismicity index. In other words, there is no causal relationship between seismic activity and global warming. For comparison, we show in Fig. 1 the conditional dispersions of global temperature anomalies where ε is the distance between synchronous points of the atmospheric CO2 concentration. The causality between atmospheric carbon dioxide concentration and temperature anomalies, by contrast, is clear.
In conclusion, there is no statistical support for the proposition that seismic activity has been a cause of large-scale warming in recent decades. A parallel analysis of CO2 and temperature supports the prevailing hypothesis that this warming is substantially caused by an increase in greenhouse gas concentrations from fossil fuel burning.





