the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Inarticulate past: similarity properties of the ice–climate system and their implications for paleo-record attribution
Mikhail Y. Verbitsky
Reconstruction and explanation of past climate evolution using proxy records is the essence of paleoclimatology. In this study, we use dimensional analysis of a dynamical model on orbital timescales to recognize theoretical limits of such forensic inquiries. Specifically, we demonstrate that major past events could have been produced by physically unsimilar processes making the task of paleo-record attribution to a particular phenomenon fundamentally difficult if not impossible. It also means that any future scenario may not have a unique cause and, in this sense, the orbital timescale future may be to some extent less sensitive to specific terrestrial circumstances.
- Article
(5951 KB) - Full-text XML
- BibTeX
- EndNote
The interpretation of most prominent events of climate history such as the Middle Pleistocene transition (Ruddiman et al., 1986, Lisiecki and Raymo, 2005, Clark et al., 2021) has been an inspiration for several generations of climate modelers (see for a review Saltzman, 2002; Tziperman et al., 2006; Crucifix, 2013; Mitsui and Aihara, 2014; Paillard, 2015; Ashwin and Ditlevsen, 2015; Verbitsky et al., 2018; Willeit et al., 2019; Riechers et al., 2022). While specific physical mechanisms invoked to explain changing glacial rhythmicity vary, they all include slow changes in ocean–atmosphere governing parameters (e.g., Saltzman and Verbitsky, 1993; Raymo, 1997; Paillard and Parrenin, 2004) or glaciation parameters (Clark and Pollard, 1998). On a more general level, all these theories in fact assume slow changes in the intensities of positive (such as long-term variations in carbon dioxide concentration, e.g., Saltzman and Verbitsky, 1993) or negative (for example, regolith erosion, Clark and Pollard, 1998, or the diminished role of the geothermal heat flux relative to the vertical temperature advection in growing ice sheets, Verbitsky and Crucifix, 2021) system feedbacks. Though all physical phenomena invoked are, indeed, real and may be plausible, the following question still remains unanswered: is it possible to disambiguate the past and elevate a single “correct” theory? Answering this question is the goal of our study.
Indeed, this is the classical attribution challenge that has been successfully addressed in the context of another well-known problem of geophysics: the causality of the observed global warming. For this purpose, the most comprehensive space-resolving models have been employed to reproduce observed time series under different conditions and to prove (or discredit) a candidate physical phenomenon (e.g., Stocker, 2014). Certainly, these models cannot be employed on extremely long orbital timescales (10–100 kyr) due to computational constraints. In search of an alternative, we turn here to dimensional analysis. Historically, dimensional analysis and concepts of similarity have been used for studying physical phenomena, complementing even the most sophisticated computational tools and providing physical insight in situations where physical interpretation of the higher-complexity modeling results may be difficult. Here, on orbital timescales, when we retreat from physics-abundant space-resolving models to more conceptual dynamical models, dimensional analysis may be promoted from a supporting to a more prominent role.
Several key terms need to be introduced before we outline the structure of our paper. We will be using the definitions of similarities as they have been articulated by Barenblatt (2003). Suppose we have a physical phenomenon that is governed by n physical parameters, k parameters of which are parameters with independent dimensions. Then, according to the π theorem (Buckingham, 1914), the phenomenon can be described by n−k adimensional similarity parameters π1, π2, … πi …, πn−k. We will consider two phenomena as being physically similar if they are described by identical similarity parameters π1, π2, …πi …, πn−k. The dimensionless time series of physically similar processes are also identical. If a similarity parameter πi can be excluded from the description of a physical process (a phenomenon becomes independent of it in the limit that πi tends to zero or infinity), we can talk about complete similarity of this physical process in this parameter: regardless of the parameter's specific value, the process does not depend on it. And, finally, we may observe incomplete similarity when none of similarity parameters π1, π2, … πi …, πn−k can be neglected even if they are too small (or too big), but the number of effective parameters may still be reduced because a phenomenon depends not on actual values of similarity parameters but on their products in some power degree (i.e., conglomerate similarity groups): ) (). Here αj, βj, …, λj, …, χj are power degrees of π1, π2, … πi …, πn−k involved into Πj formulation.
We are now ready to proceed with the structure of our paper. (a) First, we will introduce our dynamical model and describe the major physical processes involved. (b) Using dimensional analysis, we will define eight similarity parameters π1−π8 that completely define the model's behavior. (c) Since our system does not have a property of complete similarity in any of the individual parameters π1−π8, we will attempt to discover incomplete similarity and find conglomerate similarity groups. Unfortunately, there are no specific algorithms that can help us to determine governing conglomerate similarity groups Πj if they do indeed exist. Therefore, we will articulate such conglomerate similarity groups based on observed system behavior. (d) We will then discuss implications of our findings for the attribution challenge and illustrate our reasoning with a numerical experiment. (e) We will conclude our study with some thoughts relating our results to the real-world climate system.
For our experiments we employ the Verbitsky et al. (2018), VCV18 hereafter, dynamical model of the ice–climate system. It has been derived from the scaled mass- and heat-balance equations of the non-Newtonian ice flow, i.e., Eqs. (1) and (2), respectively, and has been combined with an energy-balance equation of the global climate temperature (Eq. 3):
Here, S (m2) is the area of glaciation, θ (∘C) is the basal ice-sheet temperature, and ω (∘C) is the global temperature of the ocean–atmosphere (rest of the climate) system. In deriving Eqs. (1) and (2) we consider ice sheets in the thin-boundary-layer approximation such that their inertial forces are negligible relative to stress gradients, and motion equations with very high accuracy can be written in a quasi-static form. For such an approximation, a characteristic ice thickness H is connected to ice area S as , where ζ (m) is a profile factor assumed to be constant (Verbitsky and Chalikov, 1986, VCV18). Further, Eq. (1) represents global ice balance , where, again, and is the surface mass influx. Equation (2) describes vertical ice temperature advection with a time scale), and Eq. (3) is the global energy-balance equation. The parameter a (m s−1) is the snow precipitation rate; FS is normalized external forcing, specifically, mid-July insolation at 65∘ N (Berger and Loutre, 1991), of the amplitude ε(m s−1) such that εFS describes the ice ablation rate due to astronomical forcing; κω is the ice ablation rate representing the cumulative effect of the global climate on ice-sheet mass balance; cθ represents ice discharge due to ice-sheet basal sliding; αω is the basal temperature response to global climate temperature change, and β[S−S0] is the basal temperature reaction to the changes in ice geometry; describes the global temperature response to ice geometry changes (e.g., albedo); κ (m s−1 ∘C−1), c (m s−1 ∘C−1), α (adimensional), β (∘C m−2), and γ (∘C m−2 s−1) are sensitivity coefficients; S0 (m2) is a reference glaciation area; and τ (s) is the timescale for ω. When orbitally forced, the model reproduced events of the last million years reasonably well, except for the interglacial of 400 kyr ago (Marine Isotopic Stage 11). The timing of all other interglacials coincides with Past Interglacial Working Group of PAGES (2016) data (VCV18).
We will now focus on the most remarkable feature of the historical records – a period P of climate response to the astronomical forcing. Indeed, it is the change in the climate variability from the predominant period P= 40 kyr to the main periods of P= 80–120 kyr that makes the Middle Pleistocene transition so extraordinary. Though the amplitude increase was considered, until recently, to be a necessary attribute of this transition, its presence in the paleo-records is now questioned (Clark et al., 2021). We begin with the dimensional analysis of the VCV18 Eqs. (1)–(3). Indeed, it has 11 governing parameters (including the amplitude ε and the period T of the external forcing). If we choose ε, T and γ to be parameters with independent dimensions, then in accordance with the π theorem a period of the system response can be fully described by eight dimensionless similarity parameters π1−π8: and
The numerical experiments with Eqs. (1)–(3) demonstrate that individual similarity parameters π1−π8 cannot be discarded using simply “too big” or “too small” arguments. It means that Eqs. (1)–(3) does not have a property of complete similarity in any of the individual parameters π1−π8. At the same time, we observed earlier (Verbitsky and Crucifix, 2020) that the period of Eqs. (1)–(3) response to the obliquity forcing of period T is mostly governed by two dimensionless parameters: by the ratio of the astronomical forcing amplitude to terrestrial ice-sheet snow precipitation rate, , and by the adimensional V number. The physical meaning of the V number in the orbital domain becomes most evident if we take a closer look at the structure of positive and negative feedbacks as they appear in Eqs. (1)–(3). The time-dependent negative feedback is proportional to the ice-sheet area size as β(S−S0). The coefficient β is defined by thermodynamical properties of an ice sheet, most importantly by the Péclet number, . is a characteristic mass influx, i.e., accumulation minus ablation, and k is ice temperature diffusivity (VCV18, Verbitsky and Crucifix, 2021). This negative feedback acts on ice-sheet mass balance with a vertical-advection time delay and is amplified by a sensitivity coefficient c that reflects the intensity of basal sliding. The time-dependent positive feedback is global temperature ω. In the orbital domain, τ≪T (π5≫1), ω is approximately proportional to ). The global temperature acts on the ice-sheet mass balance “instantly” as κω and with the vertical-advection time delay as a component of basal temperature conditions, αωc. Thus, the V number is emerging in the orbital domain as a ratio of amplitudes of time-dependent positive and negative feedbacks.
Specifically, when V∼0.75 and , the system exhibits the obliquity-period doubling. When the positive feedback and the obliquity forcing are less articulated, the system responds with the 40 kyr period. Thus, slow changes in the V number (for example, from V= 0.5 at t= 3000 kyr ago to V= 0.75 at t= 0) and of the ratio (for example, from 0.3 to 1.7 over the same time span) produce a change in the ice–climate behavior similar to the Middle Pleistocene transition.
We now notice that the V number can be presented in terms of similarity parameters π1−π8, specifically
We also experimentally established that the period doubling sustains (Ψ=2) if, under fixed and V, the period of the external forcing changes from let us say T= 35 kyr to T= 50 kyr. It can only happen if in this domain similarity parameters π7 and π8 make another conglomerate similarity group that does not depend on T, specifically.
Thus, Eq. (4) can be written as
which is the pure case of incomplete similarity as we defined it above: none of the similarity parameters can be neglected, but instead of eight governing parameters we have been able to migrate to four governing conglomerate similarity groups. Finally we may notice that for all large ice sheets. If, we set it to be constant, we can re-write Eq. (7) in a more simple form as
Recognition of governing conglomerate similarity groups is important because it provides us with a powerful insight: different combinations of similarity parameters πi may produce the same V number, i.e., physically unsimilar processes (formed by non-identical πi) may cause the same outcome. This observation is critical for our attribution challenge. Certainly, precise disambiguation of historical records is always a difficult task because even two physically similar processes having identical adimensional similarity parameters and demonstrating the same behavior may have been produced by different values of the physical parameters involved, unless these parameters are physical constants or well defined. The situation becomes especially challenging when we deal with conglomerate similarity groups because, as we just stated, the same results may be produced by non-identical similarity parameters (physically unsimilar processes). This is the theoretical limit that we aspire to expose.
We will now apply our findings to the Middle Pleistocene transition. Since the physical interpretation of the governing parameters incorporated in the conglomerate V number is very straightforward, we may observe a similar (in terms of the period-P bifurcation) system response to changes of a completely different physical nature. For example, parameter β, as we have discussed above, defines the intensity of the negative feedback and is formed as a result of interplay between vertical ice advection, internal friction, and geothermal heat flux (VCV18). An increased Péclet number of a growing ice sheet diminishes the role of the geothermal heat flux and may reduce parameter β thus increasing the V number. The same period-P bifurcation can also be caused, for example, by slow changes in the parameter γ that defines the intensity of the positive feedback and incorporates the effects of the albedo change or other atmospheric feedbacks. We solve Eqs. (1)–(3) for these two cases. In both cases we invoke a global cooling trend. In our first experiment (Fig. 1a), this trend is translated into a reduction of β, i.e., a weakening of the ice-sheet negative feedback, and a corresponding increase in the V number from V= 0.5 to V= 0.75. The increased continentality of the climate (reduced intensity of the snowfall during colder climate) is accounted by the ratio increase from 0.3 to 1.7. In the second experiment (Fig. 1b), the V number also evolves from V= 0.5 to V= 0.75, but this time it is achieved by the increased intensity of the positive feedback (γ). In both experiments, we used mid-July insolation at 65∘ N (Berger and Loutre, 1991) for the last 3 Myr as an astronomical forcing. The millennial forcing is added to εFS as a single sinusoid of 5 kyr period and doubled (2ε) amplitude. It is important to note that in the first experiment (changing a and β) only similarity parameters π1 and π6 are being changed, but in the second experiment (changing a and γ) the same changes in the V number are caused by changing π1, π3, π4, π6. It means that the processes involved in these two experiments are not physically similar. Though the time series produced in these two cases are obviously non-identical (see Fig. 1 inserts), we can observe that different physical phenomena may produce the same changes in the conglomerate V number and the same large-scale effect, i.e., the period-doubling bifurcation at about 1 Myr ago.
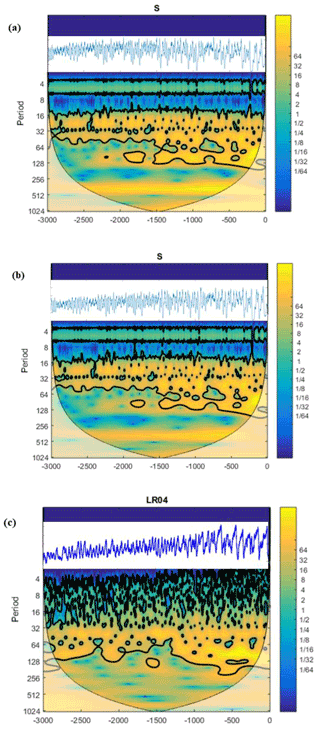
Figure 1Ice–climate system response to a cooling trend presented as an evolution of wavelet spectra over 3 Myr for calculated ice-sheet glaciation area S (106 km2) (a and b) and for the Lisiecki and Raymo (2005) benthic δ18O record (c). The V number evolves from V= 0.5 to V= 0.75 due to weakening of the negative feedback (a) and due to intensified positive feedback (b). The vertical axis is the period (kyr); the horizontal axis is time (kyr before present). The color scale shows the continuous Morlet wavelet amplitude, the thick line indicates the peaks with 95 % confidence, and the shaded area indicates the cone of influence for wavelet transform. Inserts are corresponding time series.
We do not attempt here to fully reproduce paleo-records such as Lisiecki and Raymo (2005) and a discussion of whether a period doubling should be accompanied by the amplitude increase is outside of the current paper's scope. We will just remark that the amplitude of the system response is the function of not just the period P but also of the ratio (Verbitsky and Crucifix, 2020) and, for example, less articulated continentality of colder climates may explain diminished amplitude contrasts as has been recently advocated by Clark et al. (2021).
Indeed, as we have already indicated, we used mid-July insolation at 65∘ N for the last 3 Myr as an astronomical forcing. Apart from that, these examples may also serve as an illustration of some future scenarios of the climate system behavior under post-industrial atmospheric carbon dioxide concentration reduction as implied by Ridgwell and Hargreaves (2007). Again, regardless of the physical nature of the underlying dynamical system, it exhibits a 40 kyr rhythmicity in the first 1.5 Myr of its evolution and consequent obliquity-period doubling. This probable renaissance of ice ages is different from the one envisioned by Talento and Ganapolski (2021), which is based on the model tuned to the Late Pleistocene (last 800 kyr) ice-volume data and thus postulates only 100 kyr period variability for the future.
The idea of the current presentation is simple, but its implication may be important: if the ice–climate system is defined by conglomerate similarity groups, then we may be limited in our ability to disambiguate historical records and different physical processes may produce the same future scenarios. The latter is intriguing because since Saltzman (1962) and Lorenz (1963) discovered a hydrodynamic system's sensitivity to initial conditions, the concept of deterministic chaos has become a dominant concept of weather and climate theory. Our findings suggest that if we consider orbital time scales and, instead of time series, focus on their more generalized attributes such as the period of the system response to the astronomical forcing, we may observe that the behavior of these attributes may be, to some extent, less sensitive to the physical nature of the terrestrial governing processes.
But do conglomerate similarity groups indeed govern the dynamics of the real orbital-scale climate system? So far, these groups have been found only in our VCV18 low-order dynamical model, and although this model has been explicitly derived from the conservation laws, our concept will remain hypothetical until it is supported by empirical data. We speculate, though, that existing historical records may perhaps provide some support to our theory. To evaluate the feasibility of a diagnostic approach, we entertain here a simple scaling exercise. Suppose that an empirical time series, such as a δ18O record, is created by a parent system (other than the VCV18) which is controlled by n physical parameters (k of them having independent dimensions). If we choose the period of the astronomical forcing T to be among parameters with independent dimensions, then in accordance with the π theorem we have
The wavelet spectrum of the Late Pleistocene δ18O variability in response to the precession (∼ 20 kyr period) and obliquity (∼ 40 kyr period) forcing shows the dominance of 40 kyr and 80 kyr periods (Fig. 1c). If we are willing to accept it as a hint of Ψ = 2 for T= 20 kyr and for T= 40 kyr, then, since some of the similarity parameters depend on T, the period-T independence of Ψ may only happen when π1, π2, …, πn−k make conglomerate T-independent groups. In other words, period independence of the Ψ function may be a fingerprint of conglomerate similarity groups. Indeed, the diagnostics of the Ψ function may require much more sophisticated instruments than our ad hoc reasoning, and the records will likely not explicitly reveal what the conglomerate similarity groups look like; nevertheless, their mere existence would corroborate the idea of this paper.
The MATLAB R2015b code and data to reproduce the results of the numerical experiment as they are presented in Fig. 1 are available at https://doi.org/10.5281/zenodo.6525434 (Verbitsky, 2022).
This paper refers exclusively to published research articles and their data. We refer the reader to the cited literature for access to data.
The author has declared that there are no competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The author is grateful to Michel Crucifix for multiple discussions related to this topic and to Jeremy Bassis and anonymous reviewer for their helpful comments.
This paper was edited by Anders Levermann and reviewed by Jeremy Bassis and one anonymous referee.
Ashwin, P. and Ditlevsen, P.: The middle Pleistocene transition as a generic bifurcation on a slow manifold, Clim. Dynam., 45, 2683–2695, https://doi.org/10.1007/s00382-015-2501-9, 2015.
Barenblatt, G. I.: Scaling, Cambridge University Press, Cambridge, ISBN 0 521 53394 5, 2003.
Berger, A. and Loutre, M. F.: Insolation values for the climate of the last 10 million years, Quaternary Sci. Rev., 10, 297–317, 1991.
Buckingham, E.: On physically similar systems; illustrations of the use of dimensional equations, Phys. Rev., 4, 345–376, 1914.
Clark, P. U. and Pollard, D.: Origin of the middle Pleistocene transition by ice sheet erosion of regolith, Paleoceanography, 13, 1–9, 1998.
Clark, P. U., Shakun, J., Rosenthal, Y., Köhler, P., Schrag, D., Pollard, D., Liu, Z., and Bartlein, P.: Requiem for the Regolith Hypothesis: Sea-Level and Temperature Reconstructions Provide a New Template for the Middle Pleistocene Transition, EGU General Assembly 2021, online, 19–30 Apr 2021, EGU21-13981, https://doi.org/10.5194/egusphere-egu21-13981, 2021.
Crucifix, M.: Why could ice ages be unpredictable?, Clim. Past, 9, 2253–2267, https://doi.org/10.5194/cp-9-2253-2013, 2013.
Lisiecki, L. E. and Raymo, M. E.: A Pliocene-Pleistocene stack of 57 globally distributed benthic δ18O records, Paleoceanography, 20, PA1003, https://doi.org/10.1029/2004PA001071, 2005.
Lorenz, E. N.: Deterministic nonperiodic flow, J. Atmos. Sci., 20, 130–141, 1963.
Mitsui, T. and Aihara, K.: Dynamics between order and chaos in conceptual models of glacial cycles, Clim. Dynam., 42, 3087–3099, 2014.
Paillard, D.: Quaternary glaciations: from observations to theories, Quaternary Sci. Rev., 107, 11–24, https://doi.org/10.1016/j.quascirev.2014.10.002, 2015.
Paillard, D. and Parrenin, F.: The Antarctic ice sheet and the triggering of deglaciations, Earth Planet. Sc. Lett., 227, 263–271, 2004.
Past Interglacial Working Group of PAGES: Interglacials of the last 800,000 years, Rev. Geophys., 54, 162–219, 2016.
Raymo, M.: The timing of major climate terminations, Paleoceanography, 12, 577–585, https://doi.org/10.1029/97PA01169, 1997.
Ridgwell, A., and Hargreaves, J. C.: Regulation of atmospheric CO2 by deep-sea sediments in an Earth system model, Global Biogeochem. Cy. 21, GB2008, https://doi.org/10.1029/2006GB002764, 2007.
Riechers, K., Mitsui, T., Boers, N., and Ghil, M.: Orbital insolation variations, intrinsic climate variability, and Quaternary glaciations, Clim. Past, 18, 863–893, https://doi.org/10.5194/cp-18-863-2022, 2022.
Ruddiman, W. F., Raymo, M., and McIntyre, A.: Matuyama 41,000-year cycles: North Atlantic Ocean and northern hemisphere ice sheets, Earth Planet. Sc. Lett., 80, 117–129, https://doi.org/10.1016/0012-821X(86)90024-5, 1986.
Saltzman, B.: Finite amplitude free convection as an initial value problem – I, J. Atmos. Sci., 19, 329–341, 1962.
Saltzman, B.: Dynamical paleoclimatology: generalized theory of global climate change, in: Vol. 80, Academic Press, San Diego, CA, ISBN 0 12 617331 1, 2002.
Saltzman, B. and Verbitsky, M. Y.: Multiple instabilities and modes of glacial rhythmicity in the Plio-Pleistocene: a general theory of late Cenozoic climatic change, Clim. Dynam., 9, 1–15, 1993.
Stocker, T. (Ed.): Climate change 2013: the physical science basis: Working Group I contribution to the Fifth assessment report of the Intergovernmental Panel on Climate Change, Cambridge University Press, chap. 10: Detection and Attribution of Climate Change: from Global to Regional, 867–952, ISBN 978-1-107-05799-1, ISBN 978-1-107-66182-0 2014.
Talento, S. and Ganopolski, A.: Reduced-complexity model for the impact of anthropogenic CO2 emissions on future glacial cycles, Earth Syst. Dynam., 12, 1275–1293, https://doi.org/10.5194/esd-12-1275-2021, 2021.
Tziperman, E., Raymo, M. E., Huybers, P., and Wunsch, C.: Consequences of pacing the Pleistocene 100 kyr ice ages by nonlinear phase locking to Milankovitch forcing, Paleoceanography, 21, PA4206, https://doi.org/10.1029/2005PA001241, 2006.
Verbitsky, M.: Supplementary code and data to ESD paper “Inarticulate past: similarity properties of the ice–climate system and their implications for paleo-record attribution” by M. Y. Verbitsky, Zenodo [code], https://doi.org/10.5281/zenodo.6525434, 2022.
Verbitsky, M. Y. and Chalikov, D. V.: Modelling of the Glaciers-Ocean-Atmosphere System, Gidrometeoizdat, Leningrad, edited by: Monin, A. S., 135 pp., 1986.
Verbitsky, M. Y. and Crucifix, M.: π-theorem generalization of the ice-age theory, Earth Syst. Dynam., 11, 281–289, https://doi.org/10.5194/esd-11-281-2020, 2020.
Verbitsky, M. Y. and Crucifix, M.: ESD Ideas: The Peclet number is a cornerstone of the orbital and millennial Pleistocene variability, Earth Syst. Dynam., 12, 63–67, https://doi.org/10.5194/esd-12-63-2021, 2021.
Verbitsky, M. Y., Crucifix, M., and Volobuev, D. M.: A theory of Pleistocene glacial rhythmicity, Earth Syst. Dynam., 9, 1025–1043, https://doi.org/10.5194/esd-9-1025-2018, 2018.
Willeit, M., Ganopolski, A., Calov, A., and Brovkin, V.: Mid-Pleistocene transition in glacial cycles explained by declining CO2 and regolith removal, Science Advances 5, eaav7337, https://doi.org/10.1126/sciadv.aav7337, 2019.





