Chaotic oceanic excitation of low-frequency polar motion variability

Studies of Earth rotation variations generally assume that changes in non-tidal oceanic angular momentum (OAM) manifest the ocean's direct response to atmospheric forces. However, fluctuations in OAM may also arise from chaotic intrinsic ocean processes that originate in local nonlinear (e.g., mesoscale) dynamics and can map into motions and mass variations at basin scales. To examine whether such random mass redistributions effectively excite polar motion, we compute monthly OAM anomalies from a 50-member ensemble of eddy-permitting global ocean/sea ice simulations that sample intrinsic variability through a perturbation approach on model initial conditions. The resulting OAM (i.e., excitation) functions, ${\widehat{\mathit{\chi }}}^{\mathrm{O}}$, are examined for their spread, spectral content, and role in the polar motion excitation budget from 1995 to 2015. We find that intrinsic ${\widehat{\mathit{\chi }}}^{\mathrm{O}}$ signals are comparable in magnitude to the forced component at all resolved periods except the seasonal band, amounting to ∼ 46 % of the total oceanic excitation (in terms of standard deviation) on interannual timescales. More than half of the variance in the intrinsic mass term contribution to ${\widehat{\mathit{\chi }}}^{\mathrm{O}}$ is associated with a single global mode of random bottom pressure variability, likely generated by nonlinear dynamics in the Drake Passage. Comparisons of observed interannual polar motion excitation against the sum of known surficial mass redistribution effects are sensitive to the representation of intrinsic ${\widehat{\mathit{\chi }}}^{\mathrm{O}}$ signals: reductions in the observed excitation variance can be as high as 68 % or as low as 50 % depending on the choice of the ensemble member. Chaotic oceanic excitation thus emerges as a new factor to consider when interpreting low-frequency polar motion changes in terms of core–mantle interactions or employing forward-modeled OAM estimates for Earth rotation predictions.

1 Introduction

Changes in ocean currents and the global distribution of ocean mass imply variability in oceanic angular momentum (OAM). Transfer of portions of this momentum to the solid Earth causes measurable fluctuations in the latter's rotation, comprising both changes in angular velocity and the movement of a conventional pole relative to Earth's crust – commonly referred to as wobble or polar motion (Gross, 1992). Past studies (e.g., Ponte et al., 1998; Gross et al., 2003; Bizouard and Seoane, 2010; Harker et al., 2021; Afroosa et al., 2021; Börger et al., 2023) have shown that variability in non-tidal OAM is indeed a prominent source for wobble excitation on timescales from days to several years, modulating or even exceeding the rotational contributions of other geophysical fluids. An assumption in all of these works is that the path to accurate OAM estimates is to encode known physics in a numerical ocean model and to integrate that very model in time under the necessary external (mostly atmospheric) forcings, either with or without data constraints. However, such an approach overlooks the possibility of a significant random component in the evolving ocean state, emerging internally within the fluid irrespective of atmospheric fluctuations. Evidently, any such intrinsic chaotic variability would be inaccessible – or at least challenging to capture – with the usual means of forward or inverse modeling.

A well-known example of the ocean's intrinsic variability is the nonlinear, turbulent flow as manifested in mesoscale eddies. While these eddies operate at typical scales of O(10–100) km and O(10–100) d (Rhines, 2019), their kinetic energy is known to cascade toward much larger spatial and longer temporal scales (e.g., Venaille et al., 2011; Arbic et al., 2014; Sérazin et al., 2018). In detail, ocean simulations performed in the eddying regime (at grid spacings ≤ $\mathrm{1}/\mathrm{4}$°) have demonstrated that interactions between relatively short-lived mesoscale eddies and large-scale baroclinic instability can generate chaotic interannual to secular variability in regional sea level (e.g., Llovel et al., 2018; Carret et al., 2021), large-scale volume transports (Leroux et al., 2018; Cravatte et al., 2021), or the eddy field itself (Hogg et al., 2022). Moreover, the same simulations suggest that nonlinear dynamics feed random fluctuations in ocean mass between entire basins (Zhao et al., 2023). Given this large-scale chaotic imprint on dynamical variables, intriguing questions arise as to whether oceanic intrinsic variability also affects OAM and what such random variability potentially means for the interpretation of polar motion observations.

We address these open questions using output from a $\mathrm{1}/\mathrm{4}$° large-ensemble ocean hindcast experiment, as analyzed in numerous previous studies of oceanic chaos and its inverse cascades (e.g., Leroux et al., 2018; Sérazin et al., 2018; Cravatte et al., 2021; Hogg et al., 2022). Similarly to ensemble methods in climate science (e.g., Maher et al., 2021), the member simulations are generated from a single model under identical external forcing but perturbed initial conditions, allowing one to disentangle intrinsic from forced (i.e., atmosphere-driven) variability. Emphasis is lain on the period from 1995 to 2015 and particularly the interannual band, where oceanic effects are a leading cause for wobble excitation, along with continental hydrology (Gross et al., 2003; Wińska, 2022; Börger et al., 2023). We separate the ensemble OAM estimates into forced and intrinsic components and assess their contributions to the observed wobble excitation in the presence of mass change and motion elsewhere in the Earth system. This in turn calls for a consideration of all known climatic excitations of polar motion, as described below.

2 Methods

2.1 Basic framework and data

Polar motion is a two-dimensional quantity, conventionally expressed as complex-valued angular distance $\widehat{p}=\widehat{p}\left(t\right)=p_{\mathrm{1}}+\text{i}{p}_{\mathrm{2}}$, where t indicates time and subscripts 1 and 2 refer to longitudes of 0 and 90° E in the terrestrial reference frame. Under the conservation of angular momentum (Munk and MacDonald, 1960; Moritz and Mueller, 1987), the equation governing the excitation of observed variations in $\widehat{p}$ is (e.g., Brzeziński, 1992)

$$\begin{array}{}\text{(1)}& \widehat{p}+\text{i}{\widehat{\mathit{\sigma }}}_{\mathrm{c}}^{-\mathrm{1}}\dot{\widehat{p}}=\widehat{\mathit{\chi }},\end{array}$$

where $\widehat{\mathit{\chi }}$ = χ₁+iχ₂ is the polar motion excitation function (Barnes et al., 1983; Gross, 2007), the dot denotes the time derivative, and ${\widehat{\mathit{\sigma }}}_{\mathrm{c}}$ = $\mathrm{2}\mathit{\pi }(\mathrm{1}+\text{i}/\mathrm{2}{Q}_{\mathrm{c}})/T_{\mathrm{c}}$ is the complex-valued Chandler frequency with standard values for period T_c = 433.0 d and quality factor Q_c = 179 (Gross et al., 2003). Given proper observations of $\widehat{p}$, the deconvolution on the left side of Eq. (1) yields the “geodetic” (or observed) excitation of polar motion, labeled as ${\widehat{\mathit{\chi }}}^{*}$ throughout this work. We specifically use rotation data from the daily sampled SPACE2018 series (Ratcliff and Gross, 2019) that employs a Kalman filter to adjust measurements from the primary space geodetic techniques. We remove long-period tidal effects in polar motion using the conventional model of Petit and Luzum (2010), deconvolve $\widehat{p}$, and finally average the daily ${\widehat{\mathit{\chi }}}^{*}$ values to monthly estimates.

The practical problem defined by Eq. (1) lies in identifying the causes for the observed excitation from angular momentum changes in geophysical fluids. As is customary (e.g., Wahr, 1982), we consider excitations both due to the redistribution of mass and particle movement; that is,

$$\begin{array}{}\text{(2)}& \widehat{\mathit{\chi }}={\widehat{\mathit{\chi }}}^{\mathrm{m}}+{\widehat{\mathit{\chi }}}^{\mathrm{v}},\end{array}$$

where the mass or pressure term (superscript m) accounts for perturbations in inertia products and the motion term (superscript v for velocity) represents the fluid's relative angular momentum. Formulae for computing ${\widehat{\mathit{\chi }}}^{\mathrm{m},\mathrm{v}}$ as area integrals over globally distributed mass changes and horizontal velocities are given in Appendix A. Note that these geophysical excitation functions are also called “effective angular momentum functions” (Barnes et al., 1983; Dickman, 2003), where the term “effective” pertains to the non-rigid component of the Earth's response to the excitation process. Below we occasionally refer to the oceanic $\widehat{\mathit{\chi }}$ estimate as the OAM function, thus omitting the prefix “effective” for convenience.

In comparisons with ${\widehat{\mathit{\chi }}}^{*}$, we consider excitations from four main climate system components, comprising the atmosphere (denoted to as ${\widehat{\mathit{\chi }}}^{\mathrm{A}}$), the ocean (${\widehat{\mathit{\chi }}}^{\mathrm{O}}$), the continental hydrosphere (${\widehat{\mathit{\chi }}}^{\mathrm{H}}$), and the cryosphere as represented by the Greenland and Antarctica ice sheets (${\widehat{\mathit{\chi }}}^{\mathrm{C}}$). The satellite data underlying ${\widehat{\mathit{\chi }}}^{\mathrm{H}}$ and ${\widehat{\mathit{\chi }}}^{\mathrm{C}}$, along with the ensemble approach to oceanic excitation (Sect. 2.2), constrain us to have monthly sampling. For consistency with the ocean model output analyzed here, we use atmospheric angular momentum time series from the ERA-Interim reanalysis of the European Centre for Medium-Range Weather Forecasts (Dee et al., 2011). The ${\widehat{\mathit{\chi }}}^{\mathrm{A}}$ series is an extension of a previous calculation by us (Schindelegger et al., 2013) and accounts for excitation signals associated with the ocean's inverted barometer (IB) response to atmospheric pressure loading. Figure 1 shows that, on interannual timescales (here periods ≥ 14 months¹), the atmosphere is somewhat less effective than the ocean in exciting Earth's wobbles, particularly through χ₁ (see Gross et al., 2003). Peak-to-peak amplitudes in ${\mathit{\chi }}_{\mathrm{2}}^{\mathrm{A}}$ occasionally attain 15 mas (milliarcseconds) and are largely governed by mass redistribution over Northern Hemisphere landmasses (Nastula and Salstein, 1999).

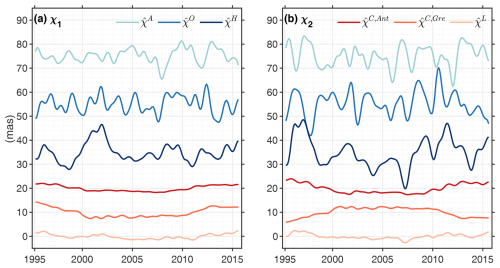
Figure 1 Modeled excitation $\widehat{\mathit{\chi }}={\mathit{\chi }}_{\mathrm{1}}+\text{i}{\mathit{\chi }}_{\mathrm{2}}$ of interannual polar motion (in milliarcseconds) from 1995 through 2015, separated into contributions from atmosphere (${\widehat{\mathit{\chi }}}^{\mathrm{A}}$, light blue), ocean (${\widehat{\mathit{\chi }}}^{\mathrm{O}}$, blue), terrestrial hydrology (${\widehat{\mathit{\chi }}}^{\mathrm{H}}$, dark blue), the Antarctic Ice Sheet (${\widehat{\mathit{\chi }}}^{\mathrm{C},\mathrm{Ant}}$, red), the Greenland Ice Sheet (${\widehat{\mathit{\chi }}}^{\mathrm{C},\mathrm{Gre}}$, orange), and gravitational attraction and loading (${\widehat{\mathit{\chi }}}^{\mathrm{L}}$, cream). Interannual signals were obtained by removing each time series' trend and seasonality and low-pass filtering the residual series with a cutoff period of 14 months. We clipped 4 months both at the beginning and at the end of the time series to avoid filter artifacts. The ${\widehat{\mathit{\chi }}}^{\mathrm{O}}$ estimate is from an arbitrary OCCIPUT ensemble member. For traceability, we compare our estimates of ${\widehat{\mathit{\chi }}}^{\mathrm{H}}$, both unfiltered and low-pass filtered, with GRACE-only ${\widehat{\mathit{\chi }}}^{\mathrm{H}}$ time series in the Supplement (Figs. S1 and S2).

Contributions to ${\widehat{\mathit{\chi }}}^{\mathrm{m}}$ from continental hydrology – or, equivalently, terrestrial water storage (TWS) – and the cryosphere are deduced from time-variable gravity fields, as practiced in previous works (e.g., Chen et al., 2013; Adhikari and Ivins, 2016; Nastula et al., 2019; Göttl et al., 2021). To cover the same 21-year period (1995–2015) as for our oceanic excitation series, we use a long-term reconstruction of monthly gravity fields based on satellite tracking data (Löcher and Kusche, 2021, updated version). The approach pursued for this reconstruction is to expand surface mass changes from the Gravity Recovery and Climate Experiment/-Follow On (GRACE/-FO; Tapley et al., 2019) mission into empirical orthogonal functions (EOFs) and use the leading EOFs as basis functions for gravity field modeling in the processing of the tracking observations. The solution has no temporal gaps and preserves the spatial resolution of GRACE/-FO gravity fields (i.e., wavelengths of ∼ 300 km) also for times prior to GRACE. We synthesize the monthly varying Stokes coefficients as equivalent water heights across Earth's surface, mask out the ocean, and partition the mass anomalies into changes over the Greenland Ice Sheet, the Antarctic Ice Sheet, and land. Spatial leakage effects near continental boundaries and ice sheet margins are mitigated using an iterative forward modeling algorithm (Chen et al., 2015); see Appendix B for details. Figure 1 illustrates that hydrological mass changes drive large (∼ 10–15 mas) interannual to intradecadal variations in polar motion excitation (Adhikari and Ivins, 2016; Meyrath and Van Dam, 2016). Detrended time series for cryospheric sources (${\widehat{\mathit{\chi }}}^{\mathrm{C}}$) reveal residual long-term drifts that bear on the accelerated melting of polar ice sheets (Chen et al., 2013; Deng et al., 2021).

In addition to ${\widehat{\mathit{\chi }}}^{\mathrm{A},\mathrm{O},\mathrm{H},\mathrm{C}}$, we account for non-uniform mass changes in the ocean due to gravitational attraction and loading (GAL), defining the excitation function ${\widehat{\mathit{\chi }}}^{\mathrm{L}}$. Processes described by GAL are the continent–ocean net mass transfer, the gravitational attraction of water toward mass anomalies anywhere in the Earth system, the crustal deformation under these loads, and the ensuing changes in Earth's gravitational field (e.g., Clarke et al., 2005). The surface mass variations arising from these effects are long-wavelength in nature, leading to small but non-negligible angular momentum changes (Quinn et al., 2015; Adhikari and Ivins, 2016, Fig. 1). We calculate the GAL effects on ocean mass and distribution by solving the sea level equation (Farrell and Clark, 1976), assuming elastic (i.e., instantaneous) deformation of a rotating Earth and a purely static adjustment in the ocean. The considered loads are gridded monthly anomalies of TWS, cryospheric mass, and IB-corrected atmospheric pressure, taken from the same sources as those adopted for our ${\widehat{\mathit{\chi }}}^{\mathrm{A},\mathrm{H},\mathrm{C}}$ estimates; see Appendix C.

2.2 Oceanic excitation

We study the externally forced and chaotic intrinsic components of oceanic excitation based on a 50-member ensemble of eddy-permitting ocean/sea ice simulations from the OceaniC Chaos – ImPacts, strUcture, predicTability (OCCIPUT) project (Penduff et al., 2014). The OCCIPUT large ensemble was generated using a global 1/4° tri-polar grid setup of the Nucleus for European Modelling of the Ocean engine for Boussinesq ocean dynamics and thermodynamics. The full ensemble hindcast spans 56 years (1960–2015). Following a common 21-year spin-up simulation, a small stochastic perturbation was applied in the density equation of each member throughout the year 1960 (Brankart et al., 2015), triggering the dispersion of the individual simulations and subsequent saturation of the ensemble spread (which occurs more quickly in turbulent, eddy-rich areas; Penduff et al., 2014; Bessières et al., 2017). These 50 realizations of the time-evolving ocean state were then integrated forward from their respective, slightly perturbed initial conditions and driven by the same 6-hourly atmospheric data from the DRAKKAR forcing set DFS 5.2 (Dussin et al., 2016), which itself is based on ERA-Interim. As the ensemble members are identical in terms of the numerical model, boundary conditions, and atmospheric forcing, their spread can be solely attributed to nonlinear ocean dynamics. Note also that the existence, origin, and spatiotemporal scales of this intrinsic variability is consistent across eddy-permitting and eddy-resolving ocean models (e.g., Sérazin et al., 2015).

To keep the involved data volumes manageable, we analyze the OCCIPUT ensemble output from 1995 to 2015 (cf. Zhao et al., 2021) and focus on monthly mean values. Specifically, we evaluate the mass and motion terms of ${\widehat{\mathit{\chi }}}^{\mathrm{O}}$ (see Appendix A) from monthly averages of ocean bottom pressure, $p_{\mathrm{b}}=p_{\mathrm{b}}\left(\mathbf{x},t\right)$, and vertically averaged northward and eastward currents, $\stackrel{\mathrm{‾}}{u}\left(\mathbf{x},t\right)$ and $\stackrel{\mathrm{‾}}{v}\left(\mathbf{x},t\right)$, where x represents horizontal space. Each of the three variables $\mathit{\xi }\left(\mathbf{x},t\right)\in \left(p_{\mathrm{b}},\stackrel{\mathrm{‾}}{u},\stackrel{\mathrm{‾}}{v}\right)$ consists of externally forced and intrinsic signals; i.e.,

$$\begin{array}{}\text{(3)}& \mathit{\xi }\left(\mathbf{x},t,\mathit{\mu }\right)={\mathit{\xi }}^{\mathrm{f}}\left(\mathbf{x},t\right)+{\mathit{\xi }}^{\mathrm{i}}\left(\mathbf{x},t,\mathit{\mu }\right),\end{array}$$

where μ is a running index over the 50 ensemble members, superscript f indicates the forced variability common to all members, and superscript i identifies the intrinsic signal. As in previous studies (see, in particular, Hogg et al., 2022), we estimate the forced component at a given month and location by the ensemble mean ${\mathit{\xi }}^{\mathrm{f}}\left(\mathbf{x},t\right)=\langle \mathit{\xi }\left(\mathbf{x},t,\mathit{\mu }\right)\rangle$, adopting 〈⋅〉 as the ensemble-mean operator. Upon separating signals as per Eq. (3), we compute angular momentum time series (Appendix A) for forced and intrinsic contributions to $\left(p_{\mathrm{b}},\stackrel{\mathrm{‾}}{u},\stackrel{\mathrm{‾}}{v}\right)$ and for their sum. Hence, intrinsic variability in oceanic excitation (abbreviated as ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$) is distinguished from forced variability (${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{f}}$) at the level of spatially distributed dynamical variables and is not based on excitation time series.

Throughout this work, p_b denotes ocean bottom pressure anomalies, obtained by removing for each ensemble member a common time-mean reference pressure field and a spatial mean p_b value per month and ensemble member. The latter correction prevents small biases or drifts in ${\widehat{\mathit{\chi }}}^{\mathrm{O}}$ caused by spurious global ocean mass changes in OCCIPUT under the Boussinesq approximation. Legitimate contributions to the globally averaged p_b, which would be removed by the correction, pertain to the freshwater flux into the ocean from atmospheric and continental sources. However, this term is accounted for through the framework of GAL and thus in ${\widehat{\mathit{\chi }}}^{\mathrm{L}}$. Note that the OCCIPUT simulations do not consider static effects, such as long-period tides or the pole tide; thus these phenomena are absent from ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{f}}$.

3 Results and discussion

3.1 Overview in spectral domain

A natural first step is to assess the magnitude and importance of the intrinsic oceanic excitation in relation to the externally forced component across a range of frequencies. In Figs. 2 and 3, we show amplitude spectra (symbol A) for ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$ (50 realizations) and ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{f}}$ (1 realization), separated into mass and motion terms and the two coordinate directions. For comparison purposes, we form chaotic amplitude fractions, R = $A_{\mathrm{i}}/A_{\mathrm{f}}$, representing the ratio of intrinsic over forced amplitude per frequency (not to be mixed up with time-invariant fractions of variance considered in previous OCCIPUT analyses, e.g., Carret et al., 2021; Hogg et al., 2022). Values of R are computed separately for (a) annual, semiannual, and terannual harmonics extracted from ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$ and ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{f}}$ and (b) the deseasonalized excitation functions. We smooth the estimated fractions under item (b) using a moving window, with window sizes decreasing (essentially linearly) from 21 frequency bins at the high end of the spectrum to 1 bin at the longest period.

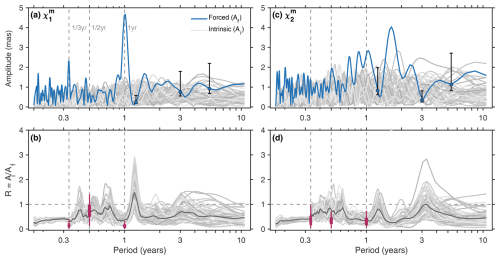
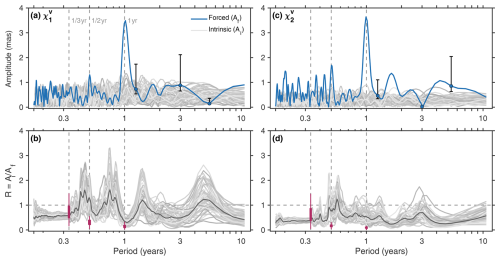
Figure 2 Spectral representation of the OCCIPUT-based estimates of intrinsic and forced oceanic excitation of polar motion, 1995–2015. Shown are amplitudes A_i and A_f (in milliarcseconds) of the intrinsic and forced oceanic mass term, ${\widehat{\mathit{\chi }}}^{\mathrm{m}}$, in (a) χ₁ and (c) χ₂, deduced from a 512-point fast Fourier transform using Welch's method (Welch, 1967). Black vertical bars indicate 68 % confidence limits for selected frequencies. Panels (b) and (d) illustrate spectrally smoothed versions of the chaotic amplitude fraction R = $A_{\mathrm{i}}/A_{\mathrm{f}}$ (dimensionless), estimated from the excitation time series with seasonal terms removed. Solid black lines mark the respective medians across the 50 realizations of R. Statistics for the annual, semiannual, and terannual terms – computed separately based on seasonal cycle fits to ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$ and ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{f}}$ – are summarized by the purple whiskers; box edges indicate the 25th and 75th percentiles, and vertical bars extend to the minimum/maximum values of seasonal R.

As apparent in Figs. 2 and 3 (panels a and c), the intrinsic oceanic excitation is embedded in a relatively flat spectrum, bounded by amplitudes of ∼ 1.5–2.0 mas in the mass term and ∼ 0.7–1.0 mas in the motion term. This spectral characteristic renders the chaotic excitation comparable in magnitude to the forced variability at most but not all frequencies. Notable exceptions occur in ${\mathit{\chi }}_{\mathrm{2}}^{\mathrm{v}}$ and wherever ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{f}}$ features peak in seasonality. Values of R are close to 0.15 for the dominant (∼ 3.5 mas) annual harmonic in both ${\mathit{\chi }}_{\mathrm{1}}^{\mathrm{v}}$ and ${\mathit{\chi }}_{\mathrm{2}}^{\mathrm{v}}$, along with similarly small fractions at periods of 1 and $\mathrm{1}/\mathrm{3}$ year in ${\mathit{\chi }}_{\mathrm{1}}^{\mathrm{m}}$. We can tentatively interpret the results for ${\mathit{\chi }}_{\mathrm{1}}^{\mathrm{m}}$ in terms of intrinsic vs. forced ratios of p_b signals from previous OCCIPUT analyses (Zhao et al., 2021). In particular, Fig. 3 of Zhao et al. (2021) places large intrinsic contributions to the seasonal p_b cycle over western boundary currents and the eddying Southern Ocean, with little sign of long-wavelength effects that would drive strong variability in ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$.

Figure 3 As in Fig. 2 but for the two components of the motion term ${\widehat{\mathit{\chi }}}^{\mathrm{v}}$.

Switching from seasonal harmonics to the broadband spectral behavior in Figs. 2 and 3, we observe a gradual increase in the chaotic amplitude fraction from ∼ 0.3 to ∼ 0.6 as periods lengthen from 60 to 120 d. This is followed at intra-annual frequencies by somewhat of a plateau of the median R near 0.9 in the mass term, along with a broadening of the ensemble spread to R ≈ 0.3–2.0 in all OAM components. The prominence of ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$ at these periods (roughly 120 to 300 d) coincides with the dominant timescale for the emergence of mesoscale eddies (Chelton et al., 2011) and the ensuing nonlinear inverse cascades (e.g., Arbic et al., 2014; O'Rourke et al., 2018; Sérazin et al., 2018). Concurrently, the forced oceanic excitation is relatively weak at intra-annual periods (especially in ${\mathit{\chi }}_{\mathrm{1}}^{\mathrm{O}}$; Figs. 2a and 3a), making this specific band another attractive (future) target for exploring the polar motion imprint of oceanic chaos. We note, though, that the intra-annual wobble excitation is largely dominated by atmospheric mass redistribution effects (Gross et al., 2003).

For the interannual signals central to this work, the spectral representations in Figs. 2 and 3 indicate appreciable power in ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$ relative to ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{f}}$, even at sub-decadal periods and particularly in ${\mathit{\chi }}_{\mathrm{1}}^{\mathrm{O}}$. Some low-frequency, intrinsic oceanic process must thus be at work at scales large enough to perturb the globally integrated OAM quantities (see Sect. 3.2). More specific to Figs. 2 and 3, we observe a number of troughs in the forced amplitude A_f that in turn afford peaks in the chaotic amplitude fractions. Such maxima in R are seen, for example, for periods T ≈ 1.2–1.3 years in all four ${\widehat{\mathit{\chi }}}^{\mathrm{O}}$ components or near 3 years in the two mass terms (spectral uncertainty is generally large, though). By contrast, the forced component exceeds the intrinsic amplitude by a factor of about 2 at T ≈ 1.6 years in both mass and motion terms of ${\mathit{\chi }}_{\mathrm{2}}^{\mathrm{O}}$. One can therefore expect any time series of interannual ${\mathit{\chi }}_{\mathrm{2}}^{\mathrm{O}}$ signals to feature stronger deterministic variability than ${\mathit{\chi }}_{\mathrm{1}}^{\mathrm{O}}$.

For a condensed view of Figs. 2 and 3, we have additionally formed ratios between intrinsic and forced standard deviations, i.e., ${\mathit{\sigma }}_{\mathrm{i}}/{\mathit{\sigma }}_{\mathrm{f}}$, calculated from ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$ and ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{f}}$ time series. Summing up mass and motion terms, and filtering the participating time series to periods ≥ 14 months, we obtain ${\mathit{\sigma }}_{\mathrm{i}}/{\mathit{\sigma }}_{\mathrm{f}}$ values of 0.50–0.83 (median 0.69) for ${\mathit{\chi }}_{\mathrm{1}}^{\mathrm{O}}$ and 0.28–0.50 (median 0.36) for ${\mathit{\chi }}_{\mathrm{2}}^{\mathrm{O}}$. Similar calculations for the complex-valued quantity ${\widehat{\mathit{\chi }}}^{\mathrm{O}}$ yield ${\mathit{\sigma }}_{\mathrm{i}}/{\mathit{\sigma }}_{\mathrm{f}}$ ratios in the range of 0.38–0.60 and a median at 0.47. When taking σ_i relative to the variability of the total oceanic excitation, the median is 0.46 in the case of ${\widehat{\mathit{\chi }}}^{\mathrm{O}}$ (range 0.43–0.50). These numbers emphasize the importance of chaotic contributions to equatorial OAM changes on timescales much longer than typically associated with the life cycles of mesoscale eddies.

3.2 Modal decomposition

Analysis of the space–time variability in modeled intrinsic p_b fields, denoted as $p_{\mathrm{b}}^{\mathrm{i}}$, can reveal more about the provenance of the chaotic OAM signals apparent in Figs. 2 and 3. Following Zhao et al. (2023), we have decomposed each of the 50 realizations of $p_{\mathrm{b}}^{\mathrm{i}}$ into real-valued EOF patterns and the associated principal components. We find a common leading EOF (mode 1 hereafter), accounting for 16 % to 22 % of the global $p_{\mathrm{b}}^{\mathrm{i}}$ variance. This particular mode, displayed exemplarily for one ensemble member in Fig. 4a, exhibits a distinct global structure, characterized by covariability across the Atlantic, the Arctic, and partly the Indian Ocean, while much of the Southern Ocean oscillates with opposite sign. The suggested origin for this mode lies in the Drake Passage (Zhao et al., 2023). Here, strong eddies and random current fluctuations, possibly involving interaction with topography (Provost et al., 2011), are thought to induce sharp bottom pressure gradients, evident in Fig. 4a between Cape Horn and the South Shetland Islands. The basin-wide $p_{\mathrm{b}}^{\mathrm{i}}$ anomalies seen elsewhere in the ocean would then be the result of fast barotropic adjustment to these local gradients along $H/f$ contours (where H is the local water depth and f is the Coriolis parameter; Zhao et al., 2023).

Figure 4 Attribution of the mass term of ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$ to global-scale intrinsic bottom pressure variability, $p_{\mathrm{b}}^{\mathrm{i}}$. Shown are (a) the leading EOF mode of $p_{\mathrm{b}}^{\mathrm{i}}$ variability (in centimeters) for ensemble member 47 and (b, c) the corresponding equatorial oceanic excitation signal (dashed black curve), obtained from synthesizing mode 1 in time and space and computing the associated OAM time series. The full intrinsic oceanic excitation, derived from $p_{\mathrm{b}}^{\mathrm{i}}$ without modal partitioning, is plotted in gray. We selected member 47 for this comparison, as its statistics in Table 1 are close to the median percentage of variance explained by mode 1 in ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$. Note that other ensemble members suggest a mode 1 structure very similar to the one shown in panel (a); see also Zhao et al. (2023).

The described processes, while different in nature to the nonlinear inverse energy cascades noted in Sect. 1, are unique in that they produce a global pattern of mass redistribution with opposite polarity between ocean basins. Such large-scale see-saws of mass have previously been shown to be an effective source of polar motion excitation (cf. Afroosa et al., 2021). We have thus synthesized monthly $p_{\mathrm{b}}^{\mathrm{i}}$ grids from mode 1 alone and deduced the corresponding oceanic excitation (that is, the oceanic mass term; Appendix A). The derived estimates of ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$ are compared in Table 1 against the full ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$ functions from OCCIPUT in terms of the percentage of variance explained (PVE). This simple evaluation demonstrates that mode 1 is indeed the leading driver for the mass component of intrinsic oceanic excitation across timescales and for both χ₁ and χ₂. Specifically, at the interannual periods of interest in this work, the OAM changes associated with $p_{\mathrm{b}}^{\mathrm{i}}$ mode 1 explain 39 % to 97 % of the variance in the ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$ mass term, with a median PVE of 63 % across the 50 ensemble members. These numbers encapsulate the idea that localized mesoscale processes somewhere in the world ocean govern variability in a truly global and geophysically relevant quantity.

Table 1 Contribution of mode 1 $p_{\mathrm{b}}^{\mathrm{i}}$ variability to the intrinsic component of the oceanic mass term, 1995–2015.^a

^a Values are percentage of variance explained (PVE) by a monthly varying ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$ mass term computed from mode 1 vs. the full intrinsic mass term. Subscript j is used to discriminate between χ₁, χ₂, and $\widehat{\mathit{\chi }}$.
^b Participating time series filtered to periods ≥ 14 months.

3.3 Interannual variability

We now examine the role of oceanic chaos in the low-frequency equatorial excitation budget over 1995–2015. To that end, Fig. 5 shows the residual geodetic excitation, obtained by subtracting from ${\widehat{\mathit{\chi }}}^{*}$ modeled contributions from the atmosphere, terrestrial hydrology, the two ice sheets, and GAL (cf. the respective time series in Fig. 1). Together, these non-oceanic sources account for 29.7 % of the variance in the full equatorial geodetic excitation (Table 2), governed in large parts by the PVE in χ₁ (51.6 %). The residual is to be compared with 51 variants of oceanic excitation from OCCIPUT, comprising both the forced component (${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{f}}$) and 50 realizations of ${\widehat{\mathit{\chi }}}^{\mathrm{O}}$ (i.e., ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{f}}+{\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$). Intrinsic processes clearly add extra variability to estimates of ${\widehat{\mathit{\chi }}}^{\mathrm{O}}$ relative to ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{f}}$, as conveyed by an ensemble spread of nearly ±5 mas throughout the analysis period. This is an important result that implies some leeway in how to evaluate and interpret the observed excitation of Earth's wobbles on interannual timescales.

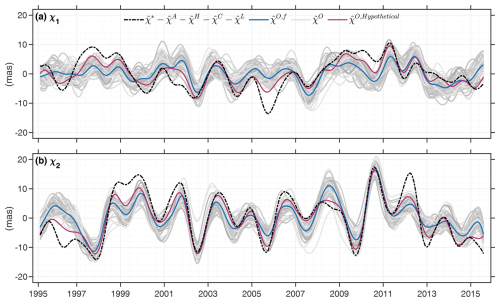
Figure 5 The low-frequency polar motion excitation budget from 1995 to 2015 in the presence of oceanic chaos. Shown are (as dashed black lines) the (a) χ₁ and (b) χ₂ components of geodetic excitation (${\widehat{\mathit{\chi }}}^{*}$) – corrected for contributions from the atmosphere (${\widehat{\mathit{\chi }}}^{\mathrm{A}}$), terrestrial hydrology (${\widehat{\mathit{\chi }}}^{\mathrm{H}}$), ice sheets (${\widehat{\mathit{\chi }}}^{\mathrm{C}}$), and GAL (${\widehat{\mathit{\chi }}}^{\mathrm{L}}$) – compared with 50 estimates of oceanic excitation from OCCIPUT (${\widehat{\mathit{\chi }}}^{\mathrm{O}}$, gray curves), the OCCIPUT ensemble mean (${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{f}}$, blue curve), and a hypothetical ensemble member (purple curve) producing the best match with the corrected geodetic excitation. All time series have been detrended, filtered to periods T ≥ 14 months, and cut back by 4 months at the two end points.

Table 2 Observed vs. modeled excitation of interannual polar motion, 1995–2015.^a, b

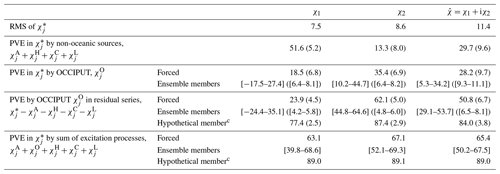
^a Values are percentage of variance explained (PVE) and the corresponding RMS of residuals (milliarcseconds) in parentheses, except for the first line. Entries for ensemble members apply to the sum of the forced and intrinsic signals. All time series have been detrended and filtered to periods T ≥ 14 months. Subscript j in the intermediate headers is used to discriminate between χ₁, χ₂, and $\widehat{\mathit{\chi }}$.
^b Replacing the SPACE2018 series in the analysis by other, more recent Earth rotation determinations changes the tabulated PVE values by 0.2 % at most.
^c Hypothetical member drawn from the ${\widehat{\mathit{\chi }}}^{\mathrm{O}}$ ensemble based on a constraint of minimum distance to the residual observed excitation; see the main text.

Adopting the forced component from OCCIPUT as a middle ground for an estimate of ${\widehat{\mathit{\chi }}}^{\mathrm{O}}$ reduces the root mean square (RMS) of the residual equatorial geodetic excitation from 9.6 to 6.7 mas (PVE = 50.8 %). Similarly, we can select from any of the 50 ensemble members as valid representations of the time-evolving ocean state and thus ${\widehat{\mathit{\chi }}}^{\mathrm{O}}$. This approach to evaluation leads to a considerable spread in the statistics in Table 2, involving a few ensemble members that exhibit slightly better skill than the forced component (minimum $\widehat{\mathit{\chi }}$ RMS of 6.5 mas, PVE = 53.7 %) but also a number of cases that reduce little variance (only 1.5 mas in RMS) in the residual geodetic excitation. A total of 15 members even yield negative PVE values in χ₁. However, these statistics are not to be taken to define absolute bounds on the efficacy of OAM in exciting low-frequency polar motion, as the intrinsic variability in any of the ensemble members is merely a random realization of the potential intrinsic variability in the real world. In fact, oceanic chaos may act to produce yet more time series of ${\widehat{\mathit{\chi }}}^{\mathrm{O}}$ that are also consistently close to the residual geodetic excitation while still lying within the ensemble spread in Fig. 5.

We have constructed such a hypothetical – but still legitimate – equatorial OAM function by identifying, month per month and in the complex plane, the particular OCCIPUT ${\widehat{\mathit{\chi }}}^{\mathrm{O}}$ sample closest to the reduced observation (i.e., ${\widehat{\mathit{\chi }}}^{*}$ minus non-oceanic sources). As one switches from one low-pass filtered member to the other, small jumps are incurred, requiring an additional round of smoothing to periods ≥ 14 months. As per design, the resulting time series follow the residual geodetic excitation more tightly than ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{f}}$ or any of the ensemble members (Fig. 5). The improved correspondence is also reflected in the PVE by the hypothetical ${\widehat{\mathit{\chi }}}^{\mathrm{O}}$ (84.0 % of the reduced geodetic excitation), leaving only 3.8 mas of interannual RMS variability unexplained. Likewise, using the hypothetical member instead of the ensemble mean in evaluating the sum of all geophysical fluid excitations against ${\widehat{\mathit{\chi }}}^{*}$ increases the PVE from 65.4 % to 89.0 %. For comparison, selecting from the original OCCIPUT members to form the total surface layer excitation yields PVE values from 50.2 % to 67.5 %. Overall, these statistics illustrate the sensitivity of such budget analysis to the representation of chaotic OAM signals.

As evident in Fig. 5, the 3.8 mas RMS signal unaccounted for in the observations is mostly made up by discrepancies between geodetic and geophysical excitations before early 2002 (i.e., the launch of GRACE), large differences throughout the year 2005 in χ₁ (to a lesser extent also 2009/2010), and a ∼ 7 mas cusp around the turn of 2011/2012 in χ₂. It is possible that part of the discrepancies arise from errors in OCCIPUT, related to, e.g., imperfectly modeled energetic circulations in the Southern Ocean (Ponte and Piecuch, 2014; Harker et al., 2021). A more likely source, though, is residual errors in the adopted gravity fields that project onto the interannual excitation budget, particularly through TWS changes and the associated fluctuations in ${\widehat{\mathit{\chi }}}^{\mathrm{H}}$. Comparing our hydrological time series in Fig. 1 with GRACE-only estimates of ${\widehat{\mathit{\chi }}}^{\mathrm{H}}$ in Fig. S2 does indeed point to differences over some of the aforementioned periods (2009/2010 in χ₁; 2011/2012 in χ₂). It therefore appears that the specifics of the gravity field reconstruction – including the limited spectral sensitivity of the involved satellites and the temporal parameterization in terms of GRACE/-FO EOFs (Löcher and Kusche, 2021) – occasionally compromise the accuracy of the derived hydrological angular momentum changes. More detailed exploration of these factors is left for future studies.

Although the geophysical models and data used in this study are necessarily imperfect, it is worth inspecting the excitation budget from yet another angle. In Fig. 6, we show amplitude spectra for the two components of ${\widehat{\mathit{\chi }}}^{*}$ minus all climate-system-related excitations, also including, for present purposes, the forced oceanic component (${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{f}}$). Spectral power in these residuals – while not well resolved within our 21-year analysis window – may be due to the said errors in the adopted angular momentum series. Alternatively, residual power may point to secondary excitation processes left out of the considerations and coming from, for example, the Earth's core (Chen et al., 2019; Ding et al., 2019; Kuang et al., 2019). Inferences along the latter lines are, however, complicated by the difficulty in accounting for the intrinsic component of oceanic excitation, ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$, as expressed by the gray background spectra in Fig. 6. In detail, the OCCIPUT ensemble suggests a likelihood for ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$ to attain amplitudes between 0 and 1.5 mas across all interannual and sub-decadal frequencies (see Figs. 2 and 3). Always selecting the most energetic ensemble member at each frequency (blue lines in Fig. 6) raises the upper bound for intrinsic effects even further, to about 2 mas.

Figure 6 Amplitude spectra (in milliarcseconds) of $\widehat{\mathit{\chi }}={\mathit{\chi }}_{\mathrm{1}}+\mathrm{i}{\mathit{\chi }}_{\mathrm{2}}$ over 1995–2015 for the intrinsic oceanic excitation (50 realizations of ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$, gray lines), in comparison to the residual geodetic excitation (dotted black line), obtained by subtracting from ${\widehat{\mathit{\chi }}}^{*}$ estimated contributions from the atmosphere, terrestrial hydrology, ice sheets, GAL, and the forced oceanic excitation (${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{f}}$); see the expression in the legend. The upper envelope of the intrinsic terms is represented by the blue line.

A 1.0–1.5 mas uncertainty in modeled wobble excitation due to oceanic chaos is generally comparable in size to the residual geodetic excitation across most frequencies (dashed black curves in Fig. 6). This prompts the question as to what extent it is possible to conclusively link such residuals to the dynamics of Earth's deep interior. For instance, Chen et al. (2019) suggested that an ∼ 2 mas oscillation with a period of T = 5.9 years (left after correcting the observed excitation over 1962–2018 for modeled atmospheric, oceanic, and hydrological effects) may be caused by the exchange of equatorial angular momentum between the outer core and the mantle via the electromagnetic torque (Kuang et al., 2019). However, analyses of satellite-derived degree-2 Stokes coefficients (Rosat et al., 2021) fail to support this idea, while our Fig. 6 illustrates that a considerable portion of any interannual ${\widehat{\mathit{\chi }}}^{*}$ residual may simply be due to mis-modeled oceanic effects. Furthermore, the possibility of intrinsic OAM signals exciting polar motion at the level of 1.0–1.5 mas even at sub-decadal periods (T = 5–10 years) adds uncertainty to attempts to detect the inner-core wobble (ICW; Rochester and Crossley, 2009) from rotation data. Recent studies (e.g., Ding et al., 2019) have made the case for an 8.7-year prograde harmonic in residual polar motion to be the signature of the ICW, at an amplitude of just 2.67±0.04 mas. However, the OAM product used by Ding et al. (2019) to remove oceanic contributions from the observations did not account for intrinsic variability, implying that the error bars on the inferred ICW amplitude are likely too optimistic. Substantiating the evidence for core effects in polar motion data on sub-decadal timescales will most certainly require further improvements in modeling surface layer processes, comprising in particular oceanic and hydrological angular momentum changes (Rosat et al., 2021; Rekier et al., 2022).

4 Summary and conclusions

The 50-member OCCIPUT ensemble investigated in this study advocates for a prominent role of oceanic intrinsic variability in equatorial OAM changes from intraseasonal to interannual timescales. This marks the arrival of a new player on the scene of Earth rotation variations, with implications for tests of closure in the polar motion excitation budget and as yet unmodeled geophysical processes (Table 2 and Fig. 6). In terms of attribution, we have been able to relate most of the mass-driven signals in ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$ (median PVE = 63 % at periods ≥ 14 months) to one particular mode of intrinsic p_b variations that likely manifests the free barotropic adjustment of the main ocean basins to nonlinearly induced p_b anomalies near the Drake Passage (cf. Fig. 4 and Zhao et al., 2023). As in many other parts of the Southern Ocean, low-frequency changes in eddy activity around the Drake Passage are strongly random in character (Hogg et al., 2022), thus providing a plausible explanation as to why variability in ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$ is a considerable fraction (43 %–50 %; see Sect. 3.1) of the total oceanic excitation of polar motion even on interannual timescales. A caveat to be acknowledged, though, is that all of these inferences are based on simulations. The credibility of OCCIPUT-based OAM series is, however, clear from Table 2, and comparisons with monthly GRACE/-FO fields have shown that the leading $p_{\mathrm{b}}^{\mathrm{i}}$ mode inherent to the ensemble could be present in satellite observations (Zhao et al., 2023). In addition, the Southern Ocean eddy field in the 1/4° OCCIPUT runs is slightly less intense than in altimetry data (Carret et al., 2021; Hogg et al., 2022), suggesting that our estimates for the chaotic contribution to wobble excitation are of a rather conservative nature.

Our results underscore the challenge of accurately representing oceanic effects for polar motion studies. In general, high horizontal model resolution (≤ $\mathrm{1}/\mathrm{4}$°) is preferred in accounting for wind-driven OAM changes (Harker et al., 2021). However, a single high-resolution baroclinic model run would also produce one specific realization of the intrinsic component that is unlikely to match the phase of the observed one. Conversely, pursuing a probabilistic approach with a large eddy-permitting ensemble such as OCCIPUT may be computationally impracticable, especially on an operational basis and at the (sub-)daily resolution now common for rotation studies (Dobslaw and Dill, 2018). Better constraining the chaotic component of ${\widehat{\mathit{\chi }}}^{\mathrm{O},\mathrm{i}}$ will most certainly require an eddying ocean model assimilating, amongst other observations, altimetric sea level anomalies and GRACE/-FO estimates of p_b (i.e., extensions of the ocean reanalyses analyzed in Börger et al., 2023). In the absence of such frameworks, the ensemble spreads and statistics presented in the present work provide indications of the errors incurred by methods that neglect intrinsic OAM variations. We expect these error quantifications to be useful for prediction purposes (e.g., Dobslaw and Dill, 2018; Kiani Shahvandi et al., 2022) and for the geophysical interpretation of the residual geodetic excitation of polar motion from intraseasonal to sub-decadal timescales.

Appendix A: Effective angular momentum functions

To estimate the effect of fluid angular momentum changes on low-frequency polar motion, we use the frequently cited formalism of Gross (2007):

$$\begin{array}{}\text{(A1)}& \widehat{\mathit{\chi }}={\widehat{\mathit{\chi }}}^{\mathrm{m}}+{\widehat{\mathit{\chi }}}^{\mathrm{v}}={\displaystyle \frac{\mathrm{1.100}\mathrm{\Omega }\mathrm{\Delta }\widehat{I}+\mathrm{1.608}\widehat{h}}{\mathrm{\Omega }(C-A^{\prime })}}.\end{array}$$

Here, Ω (7.292115 × 10⁻⁵ rad s⁻¹) is Earth's nominal sidereal rotation rate, C (8.0365 × 10³⁷ kg m²) and A^′ (8.0102 × 10³⁷ kg m²) are the polar and average equatorial principal moments of inertia of the Earth (including the core), $\widehat{h}=h_{\mathrm{1}}+\text{i}{h}_{\mathrm{2}}$ represents the relative angular momentum of the considered fluid, and $\mathrm{\Delta }\widehat{I}=\mathrm{\Delta }{I}_{\mathrm{13}}+\text{i}\mathrm{\Delta }{I}_{\mathrm{23}}$ is the time-dependent equatorial perturbation to third-column elements in the tensor of inertia (Moritz and Mueller, 1987). The numerical coefficients account for the responses of the mantle, fluid core, and equilibrium ocean to rotational perturbations caused by the initial excitation and also by the deformation of the solid Earth due to surface mass loading. Implicit to Eq. (A1) is the assumption of no mechanical coupling between mantle and core during polar motion fluctuations. The validity of this assumption on timescales longer than the Chandler period is somewhat contested (Dickman, 2003), but geophysical arguments (Wahr, 2005) suggest that even complete core–mantle coupling would modulate the transfer coefficients by no more than a few percent. Similarly small errors (1 %–2 %) are incurred by neglecting in Eq. (A1) the effect of mantle anelasticity on the load Love number (Wahr, 2005; Gross, 2007).

Writing $\mathrm{\Delta }\widehat{I}$ and $\widehat{h}$ in spherical polar coordinates, we have, for the ocean (cf. Gross et al., 2003),

$$\begin{array}{}\text{(A2)}& {\displaystyle }\mathrm{\Delta }\widehat{I}=-{\displaystyle \frac{a^{\mathrm{4}}}{g}}\underset{-\frac{\mathit{\pi }}{\mathrm{2}}}{\overset{\frac{\mathit{\pi }}{\mathrm{2}}}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}{p}_{\mathrm{b}}\sin \mathit{\varphi }{\cos }^{\mathrm{2}}\mathit{\varphi }\exp \left(\text{i}\mathit{\lambda }\right)\mathrm{d}\mathit{\lambda }\mathrm{d}\mathit{\varphi },\text{(A3)}& {\displaystyle }\widehat{h}=-a^{\mathrm{3}}{\mathit{\rho }}_{\mathrm{0}}\underset{-\frac{\mathit{\pi }}{\mathrm{2}}}{\overset{\frac{\mathit{\pi }}{\mathrm{2}}}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}\left(\stackrel{\mathrm{‾}}{u}H\sin \mathit{\varphi }+\text{i}\stackrel{\mathrm{‾}}{v}H\right)\cos \mathit{\varphi }\exp \left(\text{i}\mathit{\lambda }\right)\mathrm{d}\mathit{\lambda }\mathrm{d}\mathit{\varphi },\end{array}$$

where a is Earth's mean radius, λ and ϕ are the longitude and latitude of an arbitrary point on the Earth, g is the constant gravitational acceleration, ρ₀ is a mean seawater density (1025 kg m⁻³), and H denotes the local water depth. The quantities $\left(p_{\mathrm{b}},\stackrel{\mathrm{‾}}{u},\stackrel{\mathrm{‾}}{v}\right)$ are the dynamical variables specified in Sect. 2.2, representing either forced or intrinsic variations or their sum. Expressions analogous to Eq. (A2) exist for the mass term of other Earth system components, with pressures readily computed from equivalent water heights via the hydrostatic equation. Apart from the ocean, only the atmosphere has a non-zero motion term, usually evaluated as the volume integral over horizontal currents and densities in three-dimensional space (Barnes et al., 1983).

Appendix B: Terrestrial hydrology and cryosphere

The monthly gravity fields used for the determination of ${\widehat{\mathit{\chi }}}^{\mathrm{H}}$ and ${\widehat{\mathit{\chi }}}^{\mathrm{C}}$ over the 1995–2015 period are computed from tracking observations to up to 16 satellites from both satellite laser ranging (SLR) and the Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS) system. The problem is treated in terms of variational equations and cast as an iterative fit of forward-modeled satellite orbits to the observations. In representing the gravity field, low-degree spherical harmonics are combined with EOFs derived by principal component analysis of GRACE/-FO gravity fields. This hybrid representation, developed in Löcher and Kusche (2021), allows the same effective wavelengths as the GRACE/-FO solutions while reducing the number of parameters to an amount appropriate for techniques less sensitive to gravity field details. As the approach leaves some scope for the choice of the base functions, the monthly fields in this study are computed as weighted means of 15 solutions employing various numbers of EOFs (up to 14) and spherical harmonics (from degrees 2 to 5).

The coordinates of the SLR and DORIS stations entering the solution are part of the International Reference Frame 2014 (ITRF2014; Altamimi et al., 2016), corrected for tidal and non-tidal loading as appropriate. The force modeling for all satellites accounts for pole tides as per conventions (Petit and Luzum, 2010) and ocean pole tides following Desai (2002). Short-term mass variations in atmosphere and ocean are removed via the GRACE dealiasing product AOD1B RL06 (the GAC coefficients; Dobslaw et al., 2017) except for degree-1 terms. Furthermore, the force model includes the gravitational effect of glacial isostatic adjustment (GIA) based on the model of A et al. (2013); the choice of another GIA estimate has negligible effects on our polar motion results. For consistency, we also remove the A et al. (2013) model from the GRACE/-FO solutions prior to expanding them into EOFs. Neither GIA nor the AOD1B product is restored to the final gravity fields. Co- and post-seismic deformation signals are left uncorrected.

In a subsequent step, we also deduce degree-1 coefficients (i.e., geocenter displacements) by keeping the gravity field invariant and estimating station coordinates for all SLR sites using a no-net-rotation condition. The common mode of translation across the derived stations reveals the time-variable offset of the geocenter relative to the ITRF2014. Over the GRACE/-FO time span, our degree-1 time series is very similar to, but somewhat noisier than, the widely used estimate of Swenson et al. (2008). Prior to assigning this geocenter model to the monthly solutions, we subtract degree-1 contributions from the atmosphere (based on ERA-Interim with IB) and the ocean (based on forced OCCIPUT p_b). This correction avoids the double-counting of long-wavelength mass variations in our analysis, associated in particular with atmospheric pressure changes over land.

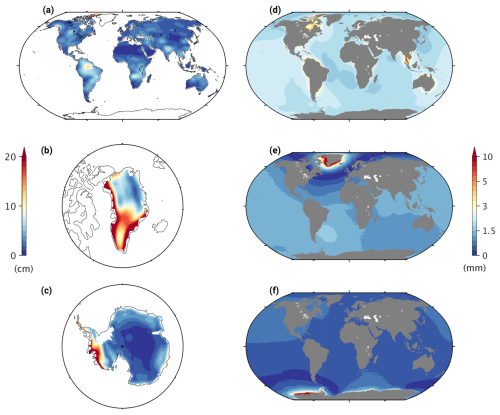
Figure B1 Standard deviation of (a–c) interannual surface mass changes over continents, as deduced from long-term gravity field solutions, and (d–f) associated GAL-induced mass redistribution in the ocean, from 1995 to 2015. Mass and GAL signals are depicted separately for (a, d) land hydrology, (b, e) Greenland, and (c, f) Antarctica. Units are centimeter of equivalent water height. Trends, seasonal oscillations, and sub-annual signals have been removed from each grid point's time series and therefore do not contribute to the figure. Note that the large (∼ 20 cm) localized mass anomaly on the northern Malay Peninsula in panel (a) is a tectonic rather than a hydrological signal; the corresponding GAL field in the area (panel b) should therefore be treated with caution.

The recovered gravity fields inherit the directional error structures (stripes) from the GRACE/-FO EOFs and thus require filtering in post-processing. We use a standard decorrelation and anisotropic smoothing kernel (DDK2; Kusche et al., 2009) to that end. Each monthly set of Stokes coefficients (including degree-1 terms) is then mapped to gridded (1° × 1°) surface mass anomalies and iteratively corrected for signal leakage across continental boundaries into the ocean. Our approach closely follows Chen et al. (2015). In short, the algorithm (a) takes a first guess of the true gridded mass distribution, (b) derives a “predicted” mass field from item (a) by expanding and re-synthesizing it using spherical harmonics up to degree 60, and (c) successively corrects the prediction – and thus the current guess for the true mass distribution – to yield closer agreement with the particular month's observed mass anomalies. The latter also defines the first guess but with values over the ocean replaced by their spatial mean. This delineation leads to a sharp transition between the ocean and land (or ice sheets, respectively) that is kept for all guesses in the iteration. We separately iterate land, Greenland, and Antarctica, always permitting adjustments to local mass values within 600 km from the coast and correcting the spatial mean over the ocean accordingly to conserve total mass. Acceptable convergence is typically achieved after five iterations per modeled region. The resulting mass change fields, used as inputs for Eq. (A2), are illustrated in terms of their standard deviation in Figs. B1a–c.

Appendix C: Gravitational attraction and loading

To quantify the effect of surface mass loads on polar motion excitation, we combine mass load estimates from different sources, generally separated by Earth system compartment. For a precise net excitation estimate, allowance should be made for transports of water between continents and the ocean, leading to the residual excitation ${\widehat{\mathit{\chi }}}^{\mathrm{L}}$. We require our estimate of ${\widehat{\mathit{\chi }}}^{\mathrm{L}}$ to be consistent with the physics of GAL, such that the total load mass is conserved and the modeled sea level is an equipotential of Earth's gravity field (Nakiboglu and Lambeck, 1980; Quinn et al., 2015; Adhikari and Ivins, 2016). Under the assumption that these mass fluxes and gravitational effects cause no relevant dynamic variations in the ocean (e.g., Kuhlmann et al., 2011), the resultant non-uniform water mass displacements may be estimated by solving the sea level equation (Woodward, 1888; Farrell and Clark, 1976). Here, sea level is taken relative to the deformed crust, equivalent to a change in p_b in the absence of atmospheric pressure variations. We solve the sea level equation in the spectral domain based on a global fingerprint inversion framework (Rietbroek et al., 2016; Uebbing et al., 2019) that accounts for solid Earth deformation, perturbations in the gravitational potential, sea level changes due to rotational feedback from the GAL-induced mass variations, and global mass conservation. The Earth's deformation is assumed to be elastic, as is customary for sub-decadal phenomena.

We apply four different loads, comprising (a) atmospheric surface pressure variations, mass changes over (b) Greenland and (c) Antarctica, and (d) TWS anomalies over the remaining continents. The atmospheric loads are monthly mean pressures from ERA-Interim, with values over the ocean replaced by their time-varying spatial mean (cf. Quinn et al., 2015). For terms (b)–(d), we use the satellite-based and leakage-corrected surface mass estimates described in Appendix B. In adopting these loads in the sea level equation, we assume that all continental mass changes are related to variations in water (or ice) mass and consequently added to or removed from the ocean. Figure B1 illustrates the derived GAL fluctuations in space (bar the atmospheric contribution), while the total excitation signal (${\widehat{\mathit{\chi }}}^{\mathrm{L}}$) is shown in Fig. 1. On the interannual timescales considered here, the atmospheric contribution to ${\widehat{\mathit{\chi }}}^{\mathrm{L}}$ is very small, featuring a standard deviation of less than 0.20 mas.

A final, more subtle issue is that GAL effects may also arise from dynamic p_b variability, as driven by atmospheric forcing or intrinsic ocean processes, and not by land–ocean mass transfer (Vinogradova et al., 2015). These gravitational effects were omitted in the OCCIPUT simulations, so we account for them after the fact, in keeping with the ocean's tendency for an equilibrium response to body forces at periods longer than a few months. Restricting the loads to dynamic ocean mass changes simplifies the GAL algorithm to a convolution of p_b anomalies with the proper Green's function (Vinogradova et al., 2015). We have applied a spherical harmonic version of this convolution (Schindelegger et al., 2018) to a few OCCIPUT ensemble members and the p_b ensemble mean. The derived excitation series were found to differ in detail but agree in terms of their interannual peaks (∼ 1 mas in χ₁; ∼ 1.5 mas in χ₂). Thus, for the purpose of this study, we represent the ocean dynamics GAL signal using the p_b ensemble mean only and impose the implied mass redistribution on each of the 50 ensemble members. The GAL effects due to ocean dynamics are therefore contained in ${\widehat{\mathit{\chi }}}^{\mathrm{O}}$ and not in ${\widehat{\mathit{\chi }}}^{\mathrm{L}}$.