A first attempt to model global hydrology at hyper-resolution

Global hydrological models are one of the key tools that can help meet the needs of stakeholders and policy makers when water management strategies and policies are developed. The primary objective of this paper is therefore to establish a first-of-its-kind, truly global hyper-resolution hydrological model that spans a multiple-decade period (1985–2019). To achieve this, two key limitations are addressed, namely the lack of high-resolution meteorological data and insufficient representation of lateral movement of snow and ice. Thus, a novel meteorological downscaling procedure that better incorporates fine-scale topographic climate drivers is incorporated, and a snow module capable of lateral movement of frozen water resembling glaciers, avalanches, and wind movement is included. We compare this global 30 arcsec version of PCR-GLOBWB (PCR – Global Water Balance) to previously published 5 and 30 arcmin versions by evaluating simulated river discharge, snow cover, soil moisture, land surface evaporation, and total water storage against observations. We show that hyper-resolution provides a more accurate simulation of river discharge, in particular for smaller catchments. We highlight that global hyper-resolution modeling is possible with current computational resources and that hyper-resolution modeling results in more realistic representations of the hydrological cycle. However, our results also suggest that global hydrological modeling still needs to incorporate land cover heterogeneity and relevant hydrological processes at the sub-kilometer scale to provide more accurate estimates of soil moisture and evaporation fluxes.

1 Introduction

Water is a vital and crosscutting element needed to achieve a number of sustainable development goals (Vörösmarty et al., 2015; Alcamo, 2019). Accurately simulating, predicting, and forecasting the distribution, abundance, and shortage of water is therefore a crucial challenge for the hydrological community. By providing information on water resources, global hydrological models are one of the key tools that can help meet the needs of stakeholders and policy makers when water management strategies and policies are developed (Bierkens, 2015; Bierkens et al., 2015; Wood et al., 2011). Despite their usefulness, an ongoing critique is that the resolution of these models is unable to provide relevant information at scales at which adaptation strategies are implemented by stakeholders (Wada et al., 2017). In response to this criticism, there has been an effort to increase the spatial resolution of current state-of-the-art global hydrological models, and this push towards hyper-resolution hydrological models has previously been described as one of hydrology’s “grand challenges” (Bierkens et al., 2015).

The drive to develop hyper-resolution models is based on the assumption that increased resolution will realize benefits coarse-resolution counterparts cannot. Hyper-resolution global hydrological models are expected to better capture the relevant physical processes that govern the distribution and quantity of global water resources and, therefore, provide a more detailed and accurate view of the hydrological cycle (Bierkens et al., 2015; Wood et al., 2011; Beven and Cloke, 2012). An improved and more detailed understanding of the global hydrological cycle can provide a number of important benefits to the broader scientific community and society. From a scientific point of view, hyper-resolution hydrological models can facilitate progress and innovation in the fields of water quality, sediment transport, floods, and drought risk by providing much needed detailed information on the movement of water in soils, rivers, lakes, and ponds (Bierkens et al., 2015). Hyper-resolution hydrological models also promise benefits that will aid society as a whole; for instance, high-resolution hydrological data can provide stakeholders and policy makers with information on scales that are more logical and actionable (Bierkens et al., 2015; Wood et al., 2011; Beven et al., 2015).

To date, there has been noticeable progress towards a truly global hyper-resolution hydrological model; however, given the complexity of such an undertaking and the associated computational burden, hyper-resolution models have, so far, been confined to continental-scale applications (e.g., Beven et al., 2015; Hoch et al., 2023; O'Neill et al., 2021; Vergopolan et al., 2021; Chaney et al., 2021). For example, the ParFlow model has been used to simulate groundwater and surface water for the contiguous United States at a spatial resolution of approximately 1 km (Yang et al., 2023). Also for the contiguous United States, Aerts et al. (2022) analyzed how increasing the resolution from 3 km to 200 m in wflow_sbm affects predictions of river discharge. There has also been an attempt to model the European continent at 1 km resolution; Hoch et al. (2023) present a 1 km version of PCR-GLOBWB (PCR – Global Water Balance) which was used to simulate hydrological states and fluxes over a multi-decadal period. These studies have provided much needed headway towards truly global hyper-resolution modeling, but they have also brought to the fore a number of challenges that need to be overcome first.

Challenges surrounding global hyper-resolution models are related to epistemic uncertainties in input data and whether or not models at these finer resolutions can effectively capture and reproduce processes that govern water dynamics (Hoch et al., 2023; Aerts et al., 2022; Yang et al., 2023). Previous studies on continental-scale hyper-resolution models have raised the question of whether an increased resolution actually results in a more accurate representation of the water cycle; there is mixed support for this notion. For example, when modeling at spatial resolutions approaching 1 km and comparing their accuracy to more coarse-scale counterparts, river discharge is more accurately simulated in some locations, while other locations show a reduced accuracy (Hoch et al., 2023; Aerts et al., 2022). Furthermore, there are discrepancies between how different components of the water cycle respond to an increase in the model resolution. Hoch et al. (2023) determined that, as resolution increases, the fidelity of soil moisture and total evaporation as simulated with the global hydrological model decreases, even though river discharge shows an increase in accuracy when moving to finer resolutions (Hoch et al., 2023). However valuable the identification of such an inconsistency may be, perhaps more importantly, it provides for an opportunity to further understand how and why the different components of the water cycle respond to an increase in model resolution. Increases in model resolution have also highlighted the need for the inclusion of fine-scale processes that are neglected at coarser resolutions. For example, Hoch et al. (2023) report that in the absence of processes that represent the transport of frozen water through glaciers, avalanches and wind lead to unrealistic accumulations of frozen water accumulating in snow towers. Despite these challenges, continental-scale hydrological models have shown that it is possible to accurately simulate at least some components of the hydrological cycle at resolutions approaching ≈ 1 km (Hoch et al., 2023; Yang et al., 2023), albeit not yet at the global scale.

One source of uncertainty is the mismatch between model resolution and that of meteorological data used as forcing (Hoch et al., 2023). The lack of meteorological data at the appropriate resolution is a major limitation for both coarse- and fine-scale models (Wilby et al., 2000; Benedict et al., 2019; Hoch et al., 2023; Yang et al., 2023; Döll et al., 2016; Müller Schmied et al., 2014). Available reanalysis products are created at a much coarser resolution than global hydrological models and fail to represent sub-grid climate dynamics that are important in defining local hydrological patterns. As a result, downscaling climate forcing becomes necessary for global hyper-resolution hydrological models, and their accuracy is heavily dependent on how such downscaled products reflect reality. To date, the production of global climate models at resolutions discussed here is constrained by technical limitations around the storage of the large volumes of output data and computational resources required to complete such simulations (Schär et al., 2020; Karger et al., 2017). However, recently 1 km meteorological data have become available in the form of climatologies as in the case of WordClim (Fick and Hijmans, 2017) and CHELSA (Karger et al., 2017; Brun et al., 2022), which could feasibly be used to downscale coarse daily meteorological forcing data from reanalyses to the required hyper-resolution.

Given these considerations, there is a need to assess the feasibility of a truly global hyper-resolution hydrological model that relies on improved spatial representation of meteorological data and fine-scale hydrological processes. The primary objective of this paper is therefore to establish a first-of-its-kind, truly global hyper-resolution hydrological model that spans a multiple-decade period (1985–2019), thereby extending the scope of current hyper-resolution hydrological models beyond the continental scale (Hoch et al., 2023). In this novel implementation of PCR-GLOBWB, a new downscaling procedure that better incorporates fine-scale topographic climate drivers is included. In addition, this implementation incorporates a snow module capable of lateral movement of frozen water resembling glaciers, which is pertinent at higher resolutions. We compare this global 30 arcsec simulation to previously published 5 and 30 arcmin versions of PCR-GLOBWB by evaluating simulated river discharge, snow cover, soil moisture, land surface evaporation, and groundwater storage against observations. We focus on how the model represents the hydrological cycle across scales and aim to highlight where we need to focus future efforts to improve hyper-resolution hydrological modeling.

2 Methods

2.1 30 arcsec PCR-GLOBWB setup and parameterization

PCR-GLOBWB (PCR – Global Water Balance) is a global hydrological and water resource model that estimates global water stores at various resolutions. It considers both natural and human-induced factors when estimating global water stores and fluxes. The 30 arcsec PCR-GLOBWB implementation presented here is built upon a schematization that has previously been applied to continental Europe (Hoch et al., 2023). The model presented here largely follows that presented by Hoch et al. (2023), but with a significant increase in spatial expansion so that it now represents the entire globe.

The model parameterization and inputs used in the 30 arcsec implementation represent high-resolution hydrological processes where possible, and in the following sections, we provide a summary of these. For extensive details on the setup of the 30 arcsec PCR-GLOBWB implementation, we refer the reader to the original European implementation by Hoch et al. (2023).

Land surface: soil, and cover, and topography

Soil information at the 30 arcsec resolution was derived from the SoilGrids250 dataset (Hengl et al., 2017), which is originally available at the 0.002° resolution. General soil attributes from SoilGrids250 were transformed into soil hydraulic properties, such as water-holding capacity, field capacity, and wilting point using the pedotransfer functions from Balland and Arp (2005). These properties were derived at 0.002 arcdeg and upscaled to 30 arcsec by averaging and using cell area as weights. For land cover parameterization the Global Land Cover Characteristics (GLCC) database version 2.0 (Loveland et al., 2000), with the land cover classification following Olson (1994a, b) and the parameter sets from Hagemann et al. (1999) and Hagemann (2002), was used. In addition, the map of Global Food Security Support Analysis Data (GFSAD) version 1.0 (Teluguntla et al., 2016) was used to define irrigation areas at the 30 arcsec resolution. GLCC and GFSAD data are available at 30 arcsec resolution, and thus one dominant land cover type was used for the 30 arcsec resolution. This differs in the 30 and 5 arcmin versions of PCR-GLOBWB, where each grid cell was divided into fractional constituents for four land cover types consisting of tall natural vegetation, short natural vegetation, non-paddy-irrigated crops, and paddy-irrigated crops (i.e., wet rice). The state-of-the-art Multi-Error-Removed Improved-Terrain Hydro digital elevation model (MERIT Hydro DEM; Yamazaki et al., 2019) that is available at 3 arcsec resolution was used to derive topography-related information. The 3 arcsec MERIT Hydro DEM was upscaled to 30 arcsec by averaging and using cell area as weights. It is important to note that various sub-grid variability parameters, such as runoff–infiltration partitioning, interflow, groundwater recharge, and capillary rise, as well as evaporation processes (van Beek and Bierkens, 2008; van Beek, 2008; Hagemann and Gates, 2003; Todini, 1996), were derived at the 3 arcsec resolution and upscaled to the 30 arcsec, 5 arcmin, and 30 arcmin resolution.

Surface water routing: lakes, reservoirs, and drainage and river network

Lake and reservoir information was taken from the Global Lakes and Wetlands Database (GLWD) of Lehner and Döll (2004) and the Global Reservoir and Dam Database (GRanD) of Lehner et al. (2011). The drainage networks were adopted from the HydroSHEDS product (Lehner et al., 2008).

In brief, the model setup used here differs from the previous PCR-GLOBWB versions as follows: (i) the parallelization approach used by the model is updated, (ii) a novel method of downscaling coarse-scale meteorological forcing to the required 30 arcsec resolution is incorporated, (iii) the model now allows for lateral transport of snow and ice at high elevations, and (iv) an offline spin-up strategy is implemented. Together, these four changes to the model allowed us to complete a 30 arcsec PCR-GLOBWB simulation with a global extent by overcoming the computational hurdle whilst still maintaining enough similarity to the previously published versions that model outputs can be compared and evaluated in a pragmatic way.

2.1.1 Climate Forcing Downscaling Procedure

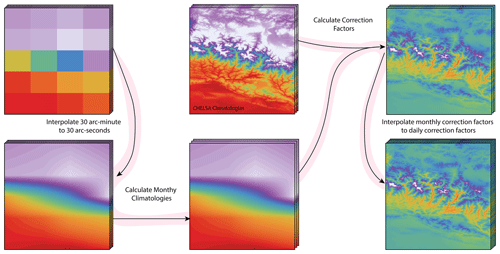
Previously published 5 arcmin and 30 arcsec versions of PCR-GLOBWB relied on a lapse-rate-centric approach to downscale meteorological forcing to the appropriate spatial resolution (Hoch et al., 2023; Sutanudjaja et al., 2011, 2018). In contrast, the current implementation relies on an alternative approach by making use of high-resolution climatologies (Karger et al., 2017). The new downscaling methodology involved bilinearly interpolating the coarse-scale meteorological forcing data to the 30 arcsec resolution, followed by the calculation of monthly climatologies from the interpolated fields. Interpolated climatologies were then compared to monthly high-resolution reference CHELSA climatologies (1981–2010; Karger et al., 2017, and Brun et al., 2022) to produce a set of Julian day-of-year correction factors that incorporated high-resolution topographic information (Fig. 1). The high-resolution climatologies represent the years 1981–2010; as such, the correction factors were calculated for this time period.

Downscaling temperature

As a first step, the coarse-scale daily temperature data (1981–2010) were interpolated to the 30 arcsec resolution using a bilinear interpolation (Tas_d). Thereafter, the interpolated values were used to calculate monthly climatologies (Tas_M) for the years 1981–2010 (Eq. 1), where N is the total number of years, m is the month, and i is the day of month.

$$\begin{array}{}\text{(1)}& {\mathrm{Tas}}_{\mathrm{M}}={\displaystyle \frac{\mathrm{1}}{N}}\sum _{j=m}^N{\mathrm{Tas}}_{d_{mi}}\end{array}$$

The interpolated monthly climatologies were then compared to the high-resolution CHELSA reference climatologies (Tas_chelsa,M), using Eq. (2), to obtain a set of monthly correction factors (CF_Tas,M).

$$\begin{array}{}\text{(2)}& {\mathrm{CF}}_{\mathrm{Tas},\mathrm{M}}={\mathrm{Tas}}_{\mathrm{chelsa},\mathrm{M}}-{\mathrm{Tas}}_{\mathrm{M}}\end{array}$$

Then, to obtain a correction factor for each Julian day of the year (CF_Tas,doy), where “doy” is day of year, we employed a linear interpolation on CF_Tas,M.

Figure 1 Procedure for downscaling meteorological forcing input date based on high-resolution climatologies.

Downscaling evaporation

Downscaling evaporation follows the same procedure as described above for temperature; coarse-scale daily data (1981–2010) were interpolated to the 30 arcsec resolution using a bilinear interpolation (ET_ref,d) and monthly climatologies (ET_ref,M) calculated for 1981–2010 (Eq. 3). Thereafter, interpolated monthly climatologies were then compared to the high-resolution reference CHELSA climatologies (ET_chelsa,M) using Eq. (4) to obtain a set of monthly correction factors (CF${}_{{\mathrm{ET}}_{\mathrm{ref},\mathrm{M}}}$). The final set of correction factors for each Julian day of the year (CF_ET,doy) was obtained through the linear interpolation of CF${}_{{\mathrm{ET}}_{\mathrm{refM}}}$. The use of a multiplicative correction factor here was in order to handle variance conservation and to obtain strictly positive values.

$$\begin{array}{}\text{(3)}& {\displaystyle }{\mathrm{ET}}_{\mathrm{ref},\mathrm{M}}={\displaystyle \frac{\mathrm{1}}{N}}\sum _{j=m}^N{\mathrm{ET}}_{\mathrm{ref},{\mathrm{d}}_{mi}}\text{(4)}& {\displaystyle }{\mathrm{CF}}_{{\mathrm{ET}}_{\mathrm{ref},\mathrm{M}}}={\mathrm{ET}}_{\mathrm{chelsa},\mathrm{M}}/{\mathrm{ET}}_{\mathrm{ref},\mathrm{M}}\end{array}$$

Downscaling precipitation

As a first step, coarse-scale daily data (1981–2010) were interpolated to the 30 arcsec resolution using a bilinear interpolation (Tp_d). For the precipitation downscaling, an additional step was necessary to correct for drizzle days. Drizzle days are erroneous by-products from interpolating precipitation, which result in very light precipitation where precipitation should be zero. To account for this and remove excess precipitation, we calculated the proportion of days in each month of the year that are dry days (dryDays) and set that proportion of bottom values in the interpolated precipitation product to 0 (Eq. 5).

$$\begin{array}{}\text{(5)}& {\mathrm{Tp}}_{\mathrm{d}}=\left\{\begin{array}{ll}{\mathrm{Tp}}_{\mathrm{d}}& \text{if }{\mathrm{Tp}}_{\mathrm{d}}\text{percentile rank is}>\text{dryDays}\\ \mathrm{0}& \text{if }{\mathrm{Tp}}_{\mathrm{d}}\text{percentile rank is}<\text{dryDays}\end{array}\right.\end{array}$$

Thereafter, the interpolated values were used to calculate climatologies (Tp_M) from 1981–2010 (Eq. 6). The interpolated monthly climatologies were then compared to the high-resolution reference climatologies (Tp_chelsa,M) using Eq. (7) to obtain a set of monthly correction factors (CF${}_{{\mathrm{Tp}}_{\mathrm{M}}}$).

$$\begin{array}{}\text{(6)}& {\displaystyle }{\mathrm{Tp}}_{\mathrm{M}}={\displaystyle \frac{\mathrm{1}}{N}}\sum _{j=m}^N{\mathrm{Tp}}_{{\mathrm{d}}_{mi}}\text{(7)}& {\displaystyle }{\mathrm{CF}}_{{\mathrm{Tp}}_{\mathrm{M}}}={\mathrm{Tp}}_{\mathrm{chelsa},\mathrm{M}}/{\mathrm{Tp}}_{\mathrm{M}}\end{array}$$

Then, to get a correction factor for each Julian day of the year (CF_Tp,doy) we employed a linear interpolation on CF${}_{{\mathrm{Tp}}_{\mathrm{M}}}$. Again, as with evaporation, the use of a multiplicative correction factor here was in order to handle variance conservation and to ensure that precipitation is positive.

2.1.2 Snow and ice transport to mimic glaciers, avalanches, and wind transport

A limitation of PCR-GLOBWB highlighted by Hoch et al. (2023) relates to how the model handles snow and ice at high elevations. Downscaled temperatures are rarely above the freezing point at higher elevations, and given that snowmelt is calculated using the degree day model, this results in unrealistic accumulations of frozen water. In reality excess snow and ice would be transported downslope by glaciers, avalanches, and wind; however, these processes are not captured in the previous versions of PCR-GLOBWB. To solve this, we included a mechanism that allows the lateral movement of frozen water to mimic the lateral and downslope transport of snow and ice by glaciers, avalanches, and wind. The snow and ice distribution component implemented here largely follows that described by Frey and Holzmann (2015). If the snow water equivalent exceeds a threshold of Hv=0.625 m, lateral transport is activated. When transport is activated, the excess (i.e., transportable) volume of frozen water in a donor cell, snow_d, is calculated from Eq. (8) and is then distributed to neighboring downslope acceptor cells as a function of slope steepness (Eq. 9). A similar approach has previously been implemented in the community water model (Burek et al., 2020).

$$\begin{array}{}\text{(8)}& {\displaystyle }{\mathrm{snow}}_{\mathrm{d}}=max(\mathrm{SWE}-\mathit{Hv},\mathrm{0})\cdot \mathrm{cellArea}\text{(9)}& {\displaystyle }{\mathrm{snow}}_{\mathrm{A}}={\displaystyle \frac{{\mathrm{snow}}_{\mathrm{d}}\cdot \frac{\tan \left(\mathrm{slope}\right)}{\mathrm{90}}}{N_{\mathrm{acceptorCells}}}}\end{array}$$

2.1.3 Spin-up strategy

Traditionally, to get an initial estimate of the water storage and fluxes, PCR-GLOBWB requires a mandatory spin-up period, during which the model is simulated for the first time step repetitively until the hydrological storage values (e.g., unsaturated and saturated zone) have converged to long-term steady states. However, when considering the computational resources required for a global 30 arcsec simulation, this approach becomes unfeasible, as times to reach equilibrium values would be very large, which is especially true for states that evolve slowly (i.e., groundwater storage). To overcome this obstacle, a three-phase spin-up process is implemented in the 30 arcsec schematization. In the first phase, PCR-GLOBWB is run for a 3-year period to obtain a representative annual groundwater recharge rate (Gw_rech). Groundwater storage is then calculated in the same way as is done by the complete model using Eq. (10) for 1000 iterations, starting with values of $\mathrm{1}\times -\mathrm{10}$ where the base flow is driven by the response time of the groundwater aquifer (j) and γ is set to a value of 1. In the third and final phase, the model is run for an additional period of 6 years with the precalculated groundwater storage values as initial conditions to obtain the final set of initial conditions.

$$\begin{array}{}\text{(10)}& \begin{array}{rl}{\mathrm{GW}}_{\mathrm{stor},i}& ={\mathrm{GW}}_{\mathrm{stor},i-\mathrm{1}}+{\mathrm{GW}}_{{\mathrm{rech}}_i}\\ & -\left[j\times \stackrel{\mathrm{‾}}{{\mathrm{GW}}_{\mathrm{stor}}}\times {\left({\displaystyle \frac{{\mathrm{GW}}_{\mathrm{stor},i-\mathrm{1}}}{\stackrel{\mathrm{‾}}{{\mathrm{GW}}_{\mathrm{stor}}}}}\right)}^{\mathit{\gamma }}\right]\end{array}\end{array}$$

2.1.4 Parallelization approach

Maintaining pragmatic and feasible simulation times is a significant challenge when considering hyper-resolution simulations. A simple yet effective parallelization technique used in the previous PCR-GLOBWB implementation is to spatially partition the modeling domain into independent hydrological units and assign separate processors to each unit, which are then completed concurrently. In the previous 5 arcmin PCR-GLOBWB, 53 independent spatial hydrological units were completed in parallel (Fig. 2a). This is possible because each basin's outlet ends up in a reservoir, endorheic lake, or ocean. This approach was followed in the current 30 arcsec implementation, where the modeling domain is split into 215 independent hydrological units, which can be completed in parallel (Fig 2b). However, at 30 arcsec, for some of the larger basins in the domain, this approach still leads to extremely long simulation times if not subdivided further – predominantly because of computationally expensive calculations associated with surface water routing. For basins exceeding an 800 000 km² threshold, a hierarchical method of parallelization was therefore used. This threshold was selected to balance efficient input/output operations and the number of point operations done by an individual processor. First, the basin is divided according to stream order so that each sub-basin is smaller than the 800 000 km² threshold. The upper reaches of the basin are completed first and then followed by the next downstream sub-basin until the last sub-basin has all the necessary information (Fig. 2c).

Figure 2 (a) Spatial domains used for parallelization in the previously published 5 arcmin PCR-GLOBWB version and (b) the domains used for the parallelization approach used in this 30 arcsec PCR-GLOBWB, which (c) requires additional dividing and hierarchical parallelization for basins exceeding 800 000 km² (displayed in gray in b). Using the Amazon as an example, hierarchical parallelization involves simulating the upper sub-basins (sub-run 1) first, followed by the intermediate sub-basins (sub-run 2) and finally the penultimate sub-basin (sub-run 3).

2.2 Global 30 arcsec PCR-GLOBWB simulation and evaluation

2.2.1 Simulation

The global 30 arcsec parameterization described above was simulated for a multi-decadal period (1985–2019) and forced with downscaled 30 arcmin W5E5 temperature, precipitation, and reference potential evaporation (Lange et al., 2021). The reference potential evaporation was calculated from the Penman–Monteith formulation, following the FAO guidelines (Allen and Food and Agriculture Organization of the United Nations, 1998), using the Python package pyEt (Vremec et al., 2021); input data for the calculation of the reference potential evaporation were also taken from W5E5. The initial conditions for this simulation were calculated following the three-part spin-up approach described above. As the first phase, PCR-GLOBWB was run from 1979–1981 with hydrological states set at an initial value of 0.001 m for water, and 1981 was taken as the representative groundwater recharge year to calculate groundwater storage offline. The model was then put through an additional spin-up period of 6 years (1979–1985) to get stable estimates of the other fluxes and storages. For final production, the initial conditions were used to run PCR-GLOBWB from 1985–2019. All simulations in this paper were run on Snellius, the Dutch National Supercomputer. We note that no calibration was performed for any of the simulations reported in this study.

To assess how capable this 30 arcsec PCR-GLOBWB is at reproducing the global hydrological cycle compared to coarser versions, two additional simulations were performed: one at 5 arcmin and the other at 30 arcmin. The same forcing and, where applicable, the same model settings were used. A spin-up period of 40 years was used. For a more thorough explanation of these two models, we refer the reader to the original publications for the 30 arcmin (van Beek, 2008; van Beek and Bierkens, 2008; Van Beek et al., 2011) and 5 arcmin variants of PCR-GLOBWB (Sutanudjaja et al., 2018). All three models were simulated for the same time period, 1985–2019, and used the same meteorological forcing; however, key differences between the model versions are highlighted in Table 1.

2.2.2 Evaluation

To provide a more comprehensive evaluation of the global simulations, multiple hydrological variables were used for evaluation, namely total water storage, total evaporation, soil moisture, snow cover, and river discharge. To compare simulations of different resolution to one another and observation data in a fair way, we opted to evaluate the simulations at scales that matched those of the observational data. Doing so allowed for an assessment of the simulated values, regardless of simulation resolution, whilst still allowing for comparisons between scales.

Global water balance and total water storage

As a first comparison between the different resolutions, we also calculated the global water balance and its respective components. In order to determine to what degree the models are able to partition water into different components of the water cycle, the global water budgets (Eq. 11) were calculated for 1985–2019:

$$\begin{array}{}\text{(11)}& \text{P}=\text{E}+Q+\mathrm{\Delta }\text{S},\end{array}$$

where P is precipitation, E is evaporation, R is runoff, and ΔS is delta storage.

This allowed us to compare mean annual fluxes of precipitation, evaporation, runoff, and change in storage for the different resolutions. In addition, runoff to precipitation and evaporation to precipitation ratios were calculated for simulations at the three different resolutions. Monthly simulated total water storage was evaluated against JPL TELLUS GRACE/GRACE-FO data for 2002–2019 (Kornfeld et al., 2019). Given the large difference in spatial resolution between the GRACE data and the simulated data, this evaluation was conducted at the basin level. GRACE data used here are at the 30 arcmin resolution, which is close to the Mascon solution provided in Kornfeld et al. (2019); however, the original resolution of GRACE is 3 arcdeg. Therefore we aimed to produce a global map of basins so that each basin contains at least four grid cells at the original 3 arcdeg resolution (i.e., the footprint of the original 3 arcdeg GRACE observations). Basin outlines were obtained from HydroBasins (Lehner and Grill, 2013), aggregation level 3, and all basins smaller than 400 000 km² were merged to neighbor basins exceeding 400 000 km². Basins that could not be merged, such as small islands, were removed. For each basin, the relative root mean sum of squares (RRMSE; Eq. 12 and Spearman's rank correlation coefficient; Eq. 13) was calculated as an indication of how well the model was able to reproduce the temporal patterns and magnitude of total water storage anomalies, respectively:

$$\begin{array}{}\text{(12)}& \mathrm{RRMSE}={\displaystyle \frac{\mathrm{RMSE}(\mathrm{obs},\mathrm{sim})}{\mathit{\sigma }\left(\mathrm{obs}\right)}},\end{array}$$

where RMSE is the root mean square error between observations (obs) and simulations (sim), and σ(obs) is the standard deviation of the observations.

$$\begin{array}{}\text{(13)}& \mathit{\rho }=\mathrm{1}-{\displaystyle \frac{\mathrm{6}\sum d_i^{\mathrm{2}}}{n(n^{\mathrm{2}}-\mathrm{1})}},\end{array}$$

Here, ρ is Spearman's rank correlation coefficient, d_i is the difference between the two ranks of each observation, and n is the number of observations.

Total evaporation and soil moisture

Total evaporation and soil moisture were evaluated against station-based observation data. Soil moisture data were obtained from the International Soil Moisture Network (Dorigo et al., 2021). In cases where multiple soil moisture measurements were present within a single day, the daily mean was calculated and used for evaluation. In addition, to ensure a good match between the modeled soil moisture depths and the observations, only data that coincided with the depth of the first soil layer were used. To match the location of observation stations with the appropriate grid cells, we located the nearest grid cell relative to the coordinates of the observation station. Observed total evaporation was obtained from the FLUXNET dataset (Pastorello et al., 2020). As with soil moisture, the observed values were matched to the simulated data by locating the nearest grid cell.

The Kling–Gupta efficiency (KGE; Eq. 14) was used to assess the accuracy of the simulated variables, and for both total evaporation and soil moisture, evaluation was restricted to stations with at least 1095 d of observation data. KGE values range from −∞ to 1.0, with values greater than −0.41 implying that the model is a better predictor than the mean of the data (Knoben et al., 2019).

$$\begin{array}{}\text{(14)}& \mathrm{KGE}=\mathrm{1}-\sqrt{(\mathit{\rho }-\mathrm{1}{)}^{\mathrm{2}}+(\mathit{\alpha }-\mathrm{1}{)}^{\mathrm{2}}+(\mathit{\beta }-\mathrm{1}{)}^{\mathrm{2}}}\end{array}$$

In addition, we analyzed how the different components of the KGE score differed between resolutions. Correlation coefficients (ρ) provide an overview of how well the model reproduces temporal changes in the observed data, the bias ratio (β) indicates differences between the means of the simulated and observed values, and the variability ratio (α) indicates how well the model replicates the variability of the observed data. A perfect KGE score is 1, which arises when all components of the score (ρ, α, and β) equal 1 (i.e., the observed and modeled values are identical). It is important to note that both observed evaporation and soil moisture are not uniformly represented across the modeling domain. Observations are denser over North America and the European continent compared to the rest of the world (Figs. A1 and A2).

Table 1 Table of key differences between the 30 arcmin, 5 arcmin, and 30 arcsec PCR-GLOBWB implementations.

Snow cover

To establish to what degree the simulations were able to reproduce snow dynamics, we evaluated daily snow cover at the 30 arcsec resolution using the MODIS daily snow cover product as observation data (Nagler et al., 2021). For this, simulated snow water equivalent was converted into snow cover, where values greater than zero were classified as having snow present and assigned a value of 1, while values equal to zero were classified as having no snow and assigned a value of zero. Given the mismatch in spatial resolution between the observation data (30 arcsec) and the 5 and 30 arcmin simulations, the 5 and 30 arcmin simulated snow cover was re-gridded to the 30 arcsec resolution using the nearest-neighbor algorithm. As an estimate of accuracy, we calculated the false alarm rate (FAR; Eq. 15), probability of detection (POD; Eq. 16), success ratio (SR; Eq. 17), and Brier score (Eq. 18). POD (perfect score =1) indicates the probability of the observed snow events being correctly forecasted, whereas FAR (perfect score =0) indicates which fractions of the simulated snow events incorrectly simulated the presence of snow when there was no snow in observed data. The SR (perfect score =1) gives information on the fraction of the observed snow events that were correctly forecasted. The Brier score (perfect score =0) was calculated for an overall assessment of the magnitude of error. These scores could conceivably be calculated for each grid cell over the entire domain; however, this would then include large regions that never experience snow and ultimately skew validation scores. Therefore, we limited the validation to regions that actually experience snowfall in reality. To do this objectively, we created a mask where snowfall was present in the simulation or the MODIS observation data and constrained the validation within the mask.

$$\begin{array}{}\text{(15)}& {\displaystyle }\text{FAR}={\displaystyle \frac{\text{false alarms}}{\text{correct negatives}+\text{false alarms}}}\text{(16)}& {\displaystyle }\text{POD}={\displaystyle \frac{\text{hits}}{\text{hits}+\text{misses}}}\text{(17)}& {\displaystyle }\text{success ratio}={\displaystyle \frac{\text{hits}}{\text{hits}+\text{false alarms}}}\text{(18)}& {\displaystyle }\text{brier score}={\displaystyle \frac{\mathrm{1}}{N}}\sum _{t=\mathrm{1}}^N{\left({\mathrm{sim}}_t-{\mathrm{obs}}_t\right)}^{\mathrm{2}}\end{array}$$

Here, sim_t is the presence or absence of snow cover in the simulation, and obs_t is the presence or absence of snow cover in the observed data for time step t.

River discharge

River discharge from the Global Runoff Data Center (GRDC) was used to evaluate river discharge simulated by PCR-GLOBWB for the three resolutions. The stations used for evaluation met the following criteria: (i) 1095 d of daily data were available, and (ii) the catchment area was greater than 5 km². Also, to make sure that the observation locations were coupled to the right tributary, we selected the relevant grid cell by matching the catchment area reported in GRDC with that of the catchment area used in the model. The grid cell within a 5 km window of the station coordinate which had a catchment area closest to that reported by GRDC was selected as the representative point. To enable comparisons between different resolutions, stations were selected based on the catchment area of the of 30 arcsec modeling domain. As the evaluation statistic, we calculated the KGE (Eq. 14) and used the value of −0.41 as the boundary value to determine whether the model improves upon the mean variable benchmark. A perfect KGE score is 1.0, and values greater than −0.41 indicate that the model is a better predictor that using the variable mean value (Knoben et al., 2019).

In addition, to obtain information on how the 30 arcsec simulation compared in relation to the 5 and 30 arcmin counterparts, we calculated the KGE skill score (Eq. 19). This allows for inferences on whether a simulation improved compared to a benchmark simulation (Towner et al., 2019). Here we assessed how the 30 arcsec simulations potentially improved upon the 30 and 5 arcmin simulations as benchmarks; a positive value indicates an improvement, and a negative value indicates a regression. To facilitate visualization and a more intuitive comparison, the bounded variant of the KGE was used so that evaluation scores range from −1 to 1 (Hallouin, 2021). In addition, this bounded variant was used to explore the relationship between elevation and catchment area; elevation was obtained from the digital elevation model within PCR-GLOBWB, and catchment area was as reported in the GRDC database.

$$\begin{array}{}\text{(19)}& {\mathrm{KGE}}_{\mathrm{ss}}={\displaystyle \frac{{\mathrm{KGE}}_{\mathrm{a}}-{\mathrm{KGE}}_{\mathrm{ref}}}{\mathrm{1}-{\mathrm{KGE}}_{\mathrm{ref}}}}\end{array}$$

3 Results

3.1 Increased resolution: computational load and insights

Increased model resolution is associated with significant increases in computational load and storage requirements (Table 2). Without parallelization a global 5 arcmin and 30 arcsec simulation would be impractical, with simulation times taking months. However, with the inclusion of a previously implemented basin-level (Sutanudjaja et al., 2018) and sub-basin-level parallelization scheme developed in this study, simulation times are now of the order of days (≈ 2.5 d) for the 5 arcmin resolution and weeks (≈ 17 d) for the 30 arcsec resolution. We also find that, unsurprisingly, storage requirements increase rapidly with increased spatial resolution. For instance, writing a single variable to disk at the daily frequency results in a 2000-fold increase in storage requirements when moving from 30 arcmin to 30 arcsec (Table 2). Storing all possible variables will equate to 365 GB for 30 arcmin, while the 30 arcsec resolution storage requirements approach the petabyte scale.

Table 2 Overview of the computational and storage requirements for a multi-decadal (1985–2019) global PCR-GLOBWB simulation at different resolutions of 30 arcmin, 5 arcmin, and 30 arcsec. Simulations were run on the Dutch National Supercomputer – Snellius.

n/a: not applicable.

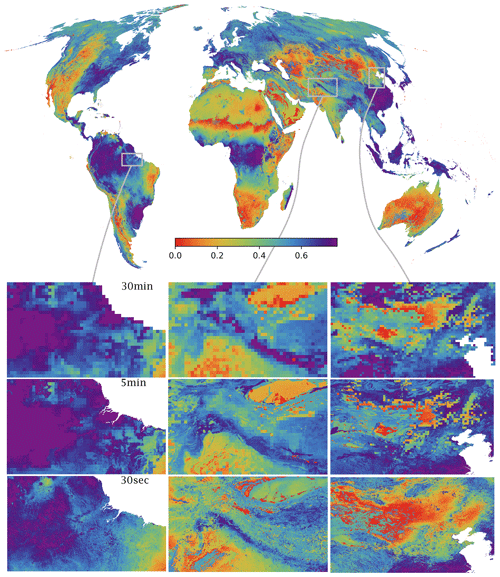
Increased model resolution does, however, provide a unique and improved representation of the hydrological cycle (Fig. 3). For instance, compared to the 5 arcmin and 30 arcsec resolution, the 30 arcsec resolution better resolves spatial patterns in soil saturation related to elevation and land cover type. In the 30 arcsec simulation, variations in soil saturation degree related to drainage networks become visible. When comparing the resolutions over the Himalayas, the 30 arcsec simulation represents a continuous field and does not display the footprint of the original coarse-scale meteorological forcing as is present at 5 and 30 arcmin resolutions (Fig. 3). In addition, when shifting focus to the Taihang mountains in mainland China, the difference between the arid Gobi towards the west and humid forests towards the east is most evident in the 30 arcsec simulation (Fig. 3).

Figure 3 Mean (1985–2019) upper soil saturation (–) simulated by PCR-GLOBWB at the 30 arcsec resolution. Zoomed insets show how the highlighted regions differ between the 30 arcsec, 5 arcmin, and 30 arcmin resolution PCR-GLOBWB simulations.

3.2 Global water balance and total water storage

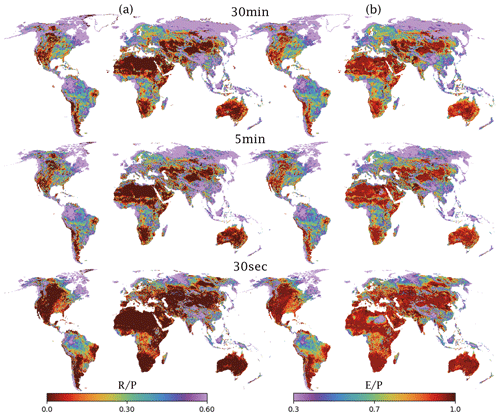
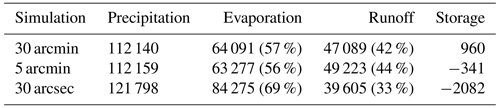
To evaluate the impact of increasing the spatial resolution on the representation of the global water cycle, we compared the long-term averages in the global water balance components. In terms of absolute values, the 30 and 5 arcmin resolutions have comparable long-term averages for the components of the water balance (Table 3); differences are attributable to variation in the total land area being simulated. In contrast, the 30 arcsec resolution shows higher precipitation and evaporation and lower runoff (Table 3).

To allow for easier comparison, we focus on relative differences. For 30 and 5 arcmin the results are comparable; however, when considering the 30 arcsec simulation, the relative evaporation rates are significantly higher and runoff significantly lower compared to the other two simulations (Table 3). As resolution increases, there is a decrease in the relative amount of precipitated water that accumulates as runoff, which is due to the increase in the relative rates of evaporation (Fig. 4).

Table 3 Global water balance components (km³ yr⁻¹) for 1985–2019 at 30 arcmin, 5 arcmin, and 30 arcsec resolution simulated by PCR-GLOBWB. Values in parentheses indicate the relative amounts in relation to precipitation as a percentage.

Spatial patterns in the models ability to reproduce total water storage anomalies are similar in the fact that for all three resolutions continental arid and high-elevation regions are less well represented in comparison to low-lying temperate, more mesic continental regions and islands (Fig. 5a). Overall, we find that, in terms of temporal dynamics, the 5 arcmin resolution best resembles the GRACE data, followed by the 30 arcsec and 30 arcmin resolution (Fig. 5b). Regarding the magnitudes of errors, the 5 arcmin resolution best resembles the GRACE data, followed by the 30 arcmin and 30 arcsec resolution (Fig. 5c).

Figure 4 Annual mean (a) runoff $/$ precipitation and (b) evaporation $/$ precipitation ratios for 30 arcmin, 5 arcmin, and 30 arcsec simulated by PCR-GLOBWB from 1985–2019.

Figure 5 (a) Spatial variation of the Spearman correlation and RRMSE for simulated total water storage validated against GRACE data from 2002–2019 for basins with areas exceeding 400 000 km². Empirical distribution functions for (b) Spearman correlations and (c) RRMSE.

3.3 Soil moisture and total evaporation

The cumulative frequency curves of KGE of simulated soil moisture are largely indistinguishable between the 30 arcmin, 5 arcmin, and 30 arcsec resolutions. Of the 1676 stations used for validation (Fig. A1), 50 % display a KGE greater than −0.41 (Fig. 6a) – this is true for all three simulations. Yet, when considering the different components of KGE, differences between model resolutions are evident. As resolution increases the correlation increases (Fig. 6b) and variability decreases (Fig. 6d); yet this is offset by an increase in bias (Fig. 6c). In contrast, total evaporation displays significant differences of the 30 arcsec simulation in comparison to the 5 and 30 arcmin simulation, whereas evaporation for 30 and 5 arcmin is similar. Only 85 % of the 143 stations (Fig. A2) display a KGE greater than −0.41 for the 30 arcsec resolution, whereas almost all of the stations in the 30 and 5 arcmin simulation exceed this threshold (Fig. 6e). This difference is attributable to an overestimation of the mean bias (Fig. 6g) and variance (Fig. 6h) of the simulated evaporation compared to observations.

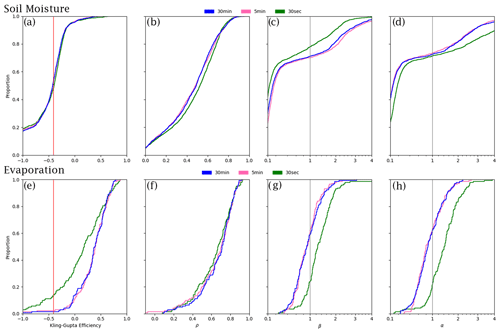
Figure 6 Top – soil moisture (a) KGE and associated constituents of KGE: (b) correlation, (c) beta, and (d) alpha from the International Soil Moisture Network (ISMN). Bottom – total evaporation (e) KGE and associated constituents of KGE: (f) correlation, (g) beta, and (h) alpha from FLUXNET. Values greater than −0.41 (red line) indicate the value at which stations improve upon the mean flow benchmark (Knoben et al., 2019).

3.4 Snow cover

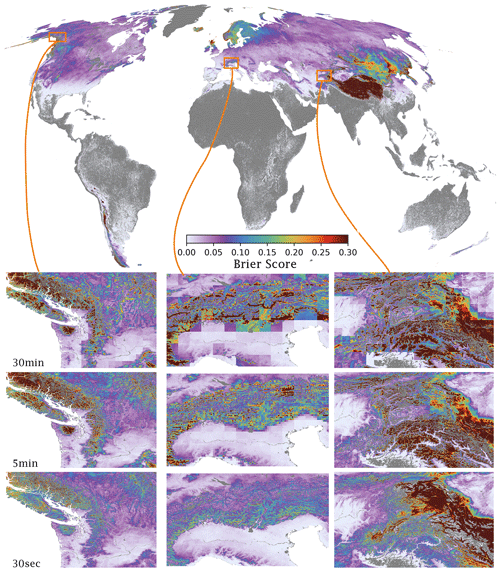
The inclusion of the lateral movement of frozen water, representative of movement by glaciers, avalanches, or wind, resulted in a more accurate accumulation and redistribution of frozen water at high elevation and prevented the erroneous accumulation of frozen water in snow towers. When evaluated against observed snow cover, all three resolutions tended to overestimate the frequency of snow cover. The 30 arcmin simulation displays the highest false alarm rate and shows an increased tendency to simulate snow on occasions where there is no snow present (Fig. 7a). As resolution increases, the false alarm rate decreases so that the simulations at 30 arcsec display the lowest false alarm rate (Fig. 7a). The success rate follows the inverse pattern of the false alarm rate, where increasing resolution results in decreased success rates (Fig. 7b). With the highest probability of detection, the 5 arcmin simulation shows the best ability to correctly simulate occasions where snow is present, followed by the 30 arcsec and 30 arcmin simulation (Fig. 7c). As an overall assessment of the resolutions in correctly simulating the presence and absence of snow, the Brier score reveals that the 30 arcsec resolutions are the most accurate, followed by the 5 and 30 arcmin resolutions (Fig. 7d).

The global distributions in the Brier score reveal that the performance varies substantially depending on location (Fig. 8). For all three resolutions, the models show the poorest performance in arid regions and regions of high elevation and complex topography. In terms of differences between resolutions, the performance increase with resolution is highest for higher elevations. However, for drier regions the performance degrades (Fig. 8).

Figure 7 (a) False alarm rate, (b) success rate, (c) probability of detection, and (d) Brier score for daily snow cover for a 30 arcmin, 5 arcmin, and 30 arcsec global PCR-GLOBWB simulation from 1985–2019.

Figure 8 Brier score of snow cover (–) simulated by PCR-GLOBWB at 30 arcsec resolution. Zoomed insets compare how the highlighted regions differ between the 30 arcsec, 5 arcmin, and 30 arcmin resolution PCR-GLOBWB simulations.

3.5 River discharge

Simulated river discharge more closely resembles the observations at the 30 arcsec resolution, with close to 80 % of the 7086 stations showing skillful discharge simulations when compared to 5 arcmin (70 %) and 30 arcmin (30 %, Fig. 9a). The improvement in the 30 arcsec simulations is mainly brought about by increases in the correlation values and reductions in the bias and variance errors (Fig. 9b, c, d). The 30 arcsec simulation improves upon the 30 and 5 arcmin simulation in the majority of locations, and this improvement is more pronounced for smaller catchments compared to larger catchments (Fig. 10a, b). The increase in performance related to resolution increase is applicable to all elevations and basins sizes, but the magnitude of performance increase is greatest for basins that are characterized by high elevations (Fig. 10c) and small catchment areas (Fig. 10d).

Figure 9 (a) KGE, (b) correlation component, (c) beta component, and (d) alpha component calculated for daily river discharge from a 30 arcmin, 5 arcmin, and 30 arcsec global PCR-GLOBWB simulation from 1985–2019. Values greater than −0.41 (red line) indicate the value at which stations improve upon the mean flow benchmark (Knoben et al., 2019).

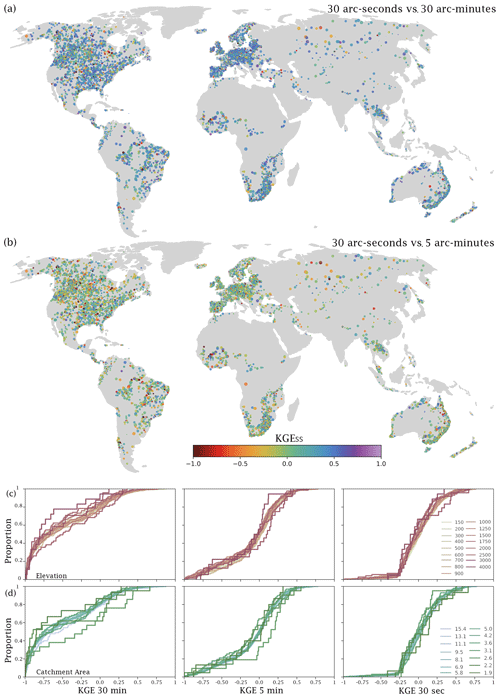
Figure 10 Spatial distribution of improvements in the KGE skill score calculated for river discharge simulated using PCR-GLOBWB at the 30 arcmin, 5 arcmin, and 30 arcsec resolution. (a) 30 arcsec vs. 30 arcmin and (b) 30 arcsec vs. 5 arcmin. KGE cumulative distribution plots for catchments binned according to elevation (c) and catchment area (d).

4 Discussion

4.1 Computational and storage demands

We show here that truly global hyper-resolution modeling is indeed possible with today's computational resources. However, long simulation times and excessive storage requirements for such simulations will hinder the reproducibility and accessibility for the wider hydrological community. Future attempts should consider how newer technologies may serve to reduce simulation times. For instance, relying on graphical processing units for computations has been shown to reduce simulation times (Freitas et al., 2022). Another opportunity lies in being able to enhance the parallelization strategies used in global hydrological models. The simulations presented here employ a common method of parallelization, termed “embarrassingly parallel”, where the modeling domain is subset into independent units (in this case basins) which are executed in parallel over multiple processes. Adopting alternative methods of parallelization may further improve simulation times, and a promising candidate called “asynchronous many tasks” (AMT) may be especially useful to the hydrological community (de Jong et al., 2022). The use of an AMT-based framework could not only improve simulation times but also reduce the ever increasing workload associated with post-simulation data management. As an illustrative example, the simulation presented here produced ∼ 46 000 files spread across 645 folders, whereas an AMT-based simulation could result in as few as 72 files output files for the same simulation.

An important motivation for the development of global hyper-resolution models is that they should be used in climate change studies (Wada et al., 2017), yet the storage and computational requirements for such an endeavor are still a limiting factor. To illustrate, here we evaluate four variables at a daily frequency and one variable at the monthly frequency, which requires approximately 27 TB of storage. To obtain a more comprehensive view of the hydrological cycle, it would be preferable to have daily-frequency data for more of the available model outputs. When considering all possible model outputs (114 variables), this would yield a storage load of approximately 1 PB for a 35-year simulation. Extending this approach for a multi-model future simulation using the CMIP6 ensemble (approximately 130 models) storage requirements is estimated at 780 PB. Petascale storage requirements are inaccessible – or at the very least impractical – for most of the hydrological community. However, expected simulation times are less daunting, and total simulation time would approach 3 months on the Dutch National Supercomputer. Although this would provide valuable information, it also means that hydrology is now faced with the same issues current general circulation models (GCMs) face, namely that, while such simulations are possible, data storage becomes a limitation (Schär et al., 2020). While solutions to the computational and storage limitations remain elusive, leveraging the recent trend towards cloud technologies for storing and disseminating Earth science data is promising, yet the costs of these services remain high (Beven et al., 2015). To this end, the hyper-resolution hydrology community can benefit by emulating and drawing from the experiences of the remote sensing community, who routinely depend on cloud computing and storage facilities to effectively distribute large volumes of data to end users (Xu et al., 2022). Moreover, hyper-resolution physically based models may also benefit from adopting similar model deployment and dissemination strategies which are common amongst the machine learning community. For example, making intermediary states (i.e., yearly states) available to the public could allow more of the community to reproduce their required model outputs on the hardware available to them.

4.2 Increasing resolution and model accuracy

By increasing the model resolution we should expect to have a better representation of hydrological systems. However, we report mixed success when looking at the reproductions of different variables; below we discuss each of the evaluated variables.

Global water budget and total water storage

Total water storage anomalies did not respond drastically to increasing model resolution, yet there were small reductions in the magnitude of error as modeling resolution is increased. This may be related to a more realistic distribution of water across the landscape at finer resolutions. Yet correlations were worse for the 30 arcmin simulation, followed by the 30 arcsec resolution, and best for the 5 arcmin simulation. However, it is also important to note that the benefits of higher resolutions may not be captured when using GRACE data to evaluate since the original resolution is 30 arcmin and thus might by itself also capture a different signature than produced by the high-resolution simulations (Hoch et al., 2023). Partitioning between the major water reserves differed in response to increasing model resolution, with a markedly larger value of evaporation and lower discharge at the highest resolution. In comparison to other global models the 30 arcsec PCR-GLOBWB rates of evaporation are within previously reported ranges (60 000–85 000 km³ yr⁻¹), whereas runoff is slightly lower than previously reported (42 000–66 000 km³ yr⁻¹; Haddeland et al., 2011). Interestingly, runoff is in line with a machine-learning-based estimate based on station-based river discharge data (Ghiggi et al., 2019). Expected evaporation to precipitation ratios are around 60 % (Miralles et al., 2011), and for the 30 arcmin (57 %) and 5 arcmin (56 %) simulations this is the case. However, for the 30 arcsec resolution the evaporation to precipitation ratios is 69 %, thus exceeding the expected value by approximately 9 percentage points.

Soil moisture and evaporation

Overall, predictions of soil moisture did not show much improvement as resolution increased, when considering the KGE scores. Differences do arise when the different components of the KGE scores are compared between the resolutions. The correlation and variability between observed and modeled soil moisture values show improvements, whilst the magnitude of negative bias increases with increasing resolution. It is important to note that the bias and variability are largely dependent on the accuracy of forcing data, and differences between simulations across resolutions could be a result of forcing and not necessarily due to differences in the model. Nonetheless, the observation that the correlation and variability are better predicted and the bias is less well predicted as resolution increases could be explained by a scenario where the model overestimates evaporation, which in turn results in soils that are too dry. In congruence, the evaporation estimates at 30 arcsec are significantly worse than those at the lower resolutions and tend toward an overestimation at 30 arcsec when compared to 5 and 30 arcmin resolution. It is feasible that this could be due to a difference in how the meteorological forcing is scaled between the resolutions or the parameterization of the model that determines the rates of evaporation. As shown hereafter in Sect. 4.3, it is likely due to the combination of parameterization and forcing effects.

Snow cover

Increasing resolution resulted in better spatial representation of snow cover, with the highest resolution presenting the highest accuracy. Increased accuracy is brought about by the reduction in instances where snow is simulated in the absence of snow in observations, a result directly related to increased resolution. Although differences are small when considering the global picture, improvements are most prominent in high-elevation regions. These improvements are related to both increasing modeling resolution and the introduction of lateral snow transport, which prevents the formation of erroneous snow towers. Although not the direct focus of this work, future studies should look at how snow can be better represented in global hydrological models by including processes that are important in determining the water dynamics in ice and snow, especially when modeling at fine spatial resolutions. For instance, the current PCR-GLOBWB does not have unique glacier implementations. Yet, glaciers have been shown to be locally and regionally important, and including such processes does result in better predictions at larger scales (Hanus et al., 2024; Wiersma et al., 2022). Similarly, work needs to be done to improve snow dynamics and move beyond the simple snowmelt model currently present in the model by including additional processes which have also been shown to increase the accuracy of predictions (Freudiger et al., 2017).

River discharge

Predictions of river discharge improved markedly as modeling resolution increased. 30 arcsec displayed the most accurate predictions of river discharge. The improvement in KGE values at higher resolution is mostly the result of a better timing of the discharge peaks and troughs, resulting in larger correlation coefficients (Fig. 10). Reductions in bias as resolution increases also contribute to improvement of river discharge; for the 30 and 5 arcmin resolution the model tends to overestimate river discharge, whilst the 30 arcsec results are underestimated. When considering that, for the 30 arcsec resolution, discharge values are underestimated in conjunction with the observation that evaporation is overestimated, the question arises of whether this increased evaporation leads to better estimates of river discharge by correcting for overestimation at the coarser resolution. Indeed, from the soil moisture and evaporation validations, we can conclude that an overestimation of evaporation may result in a better estimation of river discharge bias. A positive result from these evaluations is that smaller catchments and catchments at higher elevations are now better represented by the model, a result directly related to increased model resolution. Increased resolutions are known to better represent smaller catchments (Hoch et al., 2023; O'Neill et al., 2021; Aerts et al., 2022).

In a broader sense a direct comparison with other global hydrological models is challenging given differences in validation approaches. Heinicke et al. (2024) report that for nine global hydrological models, the median KGE for daily river discharge ranges from −0.43 to 0.46. The KGE scores presented by Heinicke et al. (2024) were based on 644 stations in comparison to the 7086 stations used in this study, so a direct comparison should be done with care; nonetheless, it is encouraging to see that even with the differences in validation approaches, the 5 arcmin (median KGE = 0.1) and 30 arcsec (median KGE = 0.1) values are within range, even with a wider set of validation stations. Regarding other hyper-resolution hydrological models, the scores reported here are similar to that of wflow_sbm implemented over the contiguous United States (median KGE = 0.0) (Aerts et al., 2022).

4.3 Untangling model scaling and forcing downscaling affects

The results above suggest the possibility that the changes in forcing, downscaling, or parameterization in the 30 arcsec model may be responsible for the patterns we observe. Namely, overestimation in evaporation leads to more accurate estimates of river discharge by correcting for an overestimation of river discharge in the 5 and 30 arcmin simulation.

Table 4 Water balance components (km³ yr⁻¹) for 1985–2019 at 30 arcmin, 5 arcmin, and 30 arcsec resolution simulated by PCR-GLOBWB over the European continent. Values in parentheses indicate the relative amounts in relation to precipitation as a percentage.

In order to differentiate between the effects of the downscaling methodology and those related to model parameterization as resolution increases, the 5 arcmin and 30 arcsec simulations, using the old and new downscaling method, were compared over continental Europe and evaluated as above (Table 4 and Fig. 11). The fact that the new downscaling method provides comparable results when comparing it to the old downscaling method at the same resolution suggests that the differences in the model results are most likely attributable to model parameterization. One likely candidate is the way in which land cover is handled within the model at the 30 arcsec resolution. For the 30 and 5 arcmin models, PCR-GLOBWB allows for sub-grid variability in land cover type, whereas at 30 arcsec only the dominant land cover type is assumed per grid cell (Table 1). This was done to reduce computation time by avoiding having to loop over land cover classes for each time step. Since forests are often the predominant type, even in agricultural landscapes, and forests generally have higher evaporation than crops, evaporation is likely overestimated through an inflated representation of forests in the model. To corroborate this claim we conducted a post hoc analysis, which was aimed at understanding which proportion of the model domain consists of forests when using dominant land cover types compared to a fractional coverage. This analysis revealed that expressing land cover as a single dominant class per grid cell leads to a 13 percentage point (Appendix B1) inflation in the total area covered by forests (∼ 50 %) compared to when using the fractional cover (∼ 37 %).

To further evaluate the sensitivity of the water budget terms to changes in land cover parameterization, for a small test region, we changed the land cover representation so that the entire region consisted of either forest, grasslands, or crops and compared the water budget terms to a 5 arcmin simulation with unchanged land cover representation (see Appendix B2). These simulations show that decreasing the relative abundance of forests within a domain will result in decreased rates of evaporation and increased rates of runoff. However, although the results for this region are quite sensitive to land cover, it is unlikely that any combination of land cover types will result in relative rates of evaporation and runoff similar to those of the coarser resolutions. This suggests that there are further factors, besides land cover representation, responsible for the difference in water budgets between resolutions. For instance, it may be that neither downscaling approach is capable of reproducing meteorology accurately at the 30 arcsec resolution.

Our results suggest that global hydrological models need to incorporate land cover heterogeneity even at the sub-kilometer scale in search of better predictive capacity. In congruence with this observation, land cover representation has previously been shown to be important in providing accurate predictions of hydrological states at the kilometer and even sub-kilometer resolution (Singh et al., 2015; Lazin et al., 2020). It is important to note that although needed for improving the accuracy of predictions, incorporating sub-kilometer land cover heterogeneity would further increase computation times. In addition, it is evident that the performance of high-resolution horological models is hindered by the availability of accurate high-resolution meteorological forcing, an observation that has previously been highlighted by more localized studies (Malle et al., 2024).

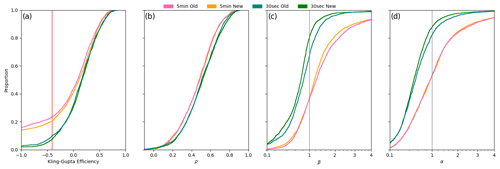
Figure 11 (a) KGE, (b) correlation component, (c) beta component, and (d) alpha component calculated for daily river discharge from a 30 arcmin, 5 arcmin, and 30 arcsec PCR-GLOBWB simulation from 1985–2019 for the European region. Values greater than −0.41 (red line) indicate the value at which stations improve upon the mean flow benchmark (Knoben et al., 2019).

4.4 Global hyper-resolution hydrological modeling: status and recommendations

Our work advances global hyper-resolution modeling and its application beyond the continental scale (Hoch et al., 2023; O'Neill et al., 2021; Vergopolan et al., 2021; Chaney et al., 2021). We show that a hyper-resolution global hydrological model is feasible given the computational limits currently in place. However, it also highlights that storage is expected to become a significant challenge as global hydrological modeling advances. This will create additional challenges when output data are used for further analysis and when extracting point location time series in a computationally effective way.

The introduction of the climatology-centered downscaling method and ability to move frozen water stores laterally result in more continuous and ultimately more realistic representations of the hydrological cycle. Hoch et al. (2023) proposed that enhancing the representation of additional physical processes at the kilometer scale could enhance the predictions. The findings presented in this study indicate that this is indeed true, although further efforts are required to further enhance the predictive capabilities. The importance of high-resolution forcing data is well understood, and it has been shown that hydrological predictions become better when more high-resolution data are used to force such models (Evin et al., 2024; Alfieri et al., 2022). Such data are only available for limited regions of the world, and obtaining global and spatially coherent high-resolution forcing data is a challenge that needs to be addressed if we are to have higher-quality hydrological predictions at the global scale.

Furthermore, as also shown by Hoch et al. (2023), there are a number of epistemic uncertainty issues related to global hydrological modeling that still need to be addressed. For instance, we need a better representation of land surface, snow, and ice processes as these processes play a dominant role at fine spatial resolution and can no longer be neglected or captured in existing conceptual parameterization. At finer spatial resolution altitude effects start to play a key role in precipitation totals, snow and ice formation, melt, and evaporation and thus require fine-resolution meteorological information if possible at the global scale.

On the other hand, moving to a higher resolution allows for a better match to in situ observations and more recently released high-resolution remote sensing products; the importance of scale commensurability between model outputs and in situ observations has been highlighted by Beven et al. (2022). For instance, the caravan dataset, which has 6830 stations for small river catchments (Kratzert et al., 2023), could be used to better underpin the accuracy of simulated river discharge values at higher resolution – as has been done for smaller-scale studies (Aerts et al., 2023). Resolutions coarser than 30 arcsec would not allow for the inclusion of these river catchments, given the disconnect between modeling resolution and observed data station sizes. In addition, recent advances in remotely sensed high-resolution soil moisture data will also be a valuable resource for evaluating hyper-resolution simulations once their time series are sufficiently long (Brocca et al., 2024).

5 Conclusions

The main goal of this study was to develop a unique global hyper-resolution hydrological model that covers a period of several decades (1985–2019), expanding the current hyper-resolution hydrological models beyond continental boundaries. We incorporated a novel downscaling approach and lateral movement of frozen water that ultimately yields more realistic representations of the hydrological cycle. Yet, as resolution increased, the model tended to overestimate rates of total evaporation, which resulted in reductions in runoff. This suggests that additional processes that are relevant at the hyper resolution need further attention. Overall, the pursuit of hyper-resolution hydrological models is driven by the assumption that they will be able to provide stakeholders with more local estimates of water resources; one promising result reported in this study is that increased resolution leads to more accurate estimates of river discharge.

Appendix A: Spatial distribution of validation stations

Figure A1 Map showing locations of stations used for validation of simulated soil moisture.

Figure A2 Map showing locations of stations used for validation of simulated total evaporation.

Appendix B: Land cover representation analysis

B1 Dominant vs. fractional

The model evaluation shows that relative rates of land evaporation are higher in the 30 arcsec simulation in comparison with the 5 and 30 arcmin simulations. We postulate that this is due to the way that the model represents land cover in the 30 arcsec simulation (Sects. 2.1 and 4.3). Given that the model we present here relies on the Global Land Cover Characteristics (GLCC) database version 2.0 (Loveland et al., 2000), which is at the 30 arcsec resolution, we cannot directly test this assumption using the model input datasets. However, higher-resolution land cover datasets are available and as such we leveraged these to test our hypothesis that using dominant land cover types leads to a higher proportion of the model domain being represented by forests than if fractional land cover types were used.

Here we rely on the Dynamic Land Cover map (100 m resolution) from the Copernicus Global Land Service (Buchhorn et al., 2020), which provides both dominant land cover types and fractional land cover types at the 100 m resolution. To test the difference between dominant and fractional, we compared to percentage of total land cover represented by forest when using the dominant land cover type compared to the fractional representation for the year 2019 (Buchhorn et al., 2020). When using the dominant land cover the total land area covered by forests amounts to 50 %; when using fractional land cover this number is much lower at 37 %, a difference of 13 percentage points.

Table B1 Water balance components (km³ yr⁻¹), evaporation to precipitation ratio, and runoff to precipitation ratio for 1985–2019 at 5 arcmin and 30 arcsec, with varying land cover parameterization, simulated by PCR-GLOBWB.

n/a: not applicable.

B2 Water budget sensitivity

In addition to the above analysis, we have also looked at how sensitive evaporation in the 30 arcsec simulation is to land cover changes for a small test region (Southern Alps). We assumed that the entire domain is covered by either forest, grassland, or croplands. These three simulations were compared to the original configuration 30 arcsec and 5 arcmin (as presented in the main text).

From this sensitivity test, we conclude that evaporation rates are indeed sensitive to changes in land cover representation; however, no changes will allow us to reach the same evaporation rates as for the 5 arcmin or the ratio between evaporation and precipitation. In addition, the evaporation estimates we present are at the higher end of what can be expected (94–130 km³ yr⁻¹). It also shows that no land cover configuration at the 30 arcsec resolution will reproduce the values at 5 arcmin, since the maximum possible runoff values at 30 arcsec (125 km³ yr⁻¹) are still lower than what is simulated by the 5 arcmin resolution (126 km³ yr⁻¹). This also means that even by changing all land cover to crops we cannot achieve the same values as for the 5 arcmin model simulations.