the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Climate–groundwater dynamics inferred from GRACE and the role of hydraulic memory
Richard G. Taylor
Chris M. Brierley
Mohammad Shamsudduha
Mark O. Cuthbert
Groundwater is the largest store of freshwater on Earth after the cryosphere and provides a substantial proportion of the water used for domestic, irrigation and industrial purposes. Knowledge of this essential resource remains incomplete, in part, because of observational challenges of scale and accessibility. Here we examine a 14-year period (2002–2016) of Gravity Recovery and Climate Experiment (GRACE) observations to investigate climate–groundwater dynamics of 14 tropical and sub-tropical aquifers selected from WHYMAP's (Worldwide Hydrogeological Mapping and Assessment Programme) 37 large aquifer systems of the world. GRACE-derived changes in groundwater storage resolved using GRACE Jet Propulsion Laboratory (JPL) mascons and the Community Land Model's land surface model are related to precipitation time series and regional-scale hydrogeology. We show that aquifers in dryland environments exhibit long-term hydraulic memory through a strong correlation between groundwater storage changes and annual precipitation anomalies integrated over the time series; aquifers in humid environments show short-term memory through strong correlation with monthly precipitation. This classification is consistent with estimates of groundwater response times calculated from the hydrogeological properties of each system, with long (short) hydraulic memory associated with slow (rapid) response times. The results suggest that groundwater systems in dryland environments may be less sensitive to seasonal climate variability but vulnerable to long-term trends from which they will be slow to recover. In contrast, aquifers in humid regions may be more sensitive to climate disturbances such as drought related to the El Niño–Southern Oscillation but may also be relatively quick to recover. Exceptions to this general pattern are traced to human interventions through groundwater abstraction. Hydraulic memory is an important factor in the management of groundwater resources, particularly under climate change.
- Article
(6463 KB) - Full-text XML
-
Supplement
(3097 KB) - BibTeX
- EndNote
The availability of freshwater is essential for sustaining human life, economic security and access to the benefits of a wide range of ecosystem services (Taylor et al., 2013a). After the cryosphere, groundwater is the second largest store of freshwater on the planet, supplying 36 % of domestic water, 42 % of irrigation for agriculture and 27 % of industrial water use (Döll et al., 2012). Bidirectional flows between surface water and groundwater are fundamentally important to the ecology of semi-arid and arid regions (drylands) where surface water often recharges groundwater and baseflow from groundwater can sustain rivers and wetlands in the absence of rainfall (Alley et al., 2002; de Graaf et al., 2019). Climate change in which anthropogenic emissions of greenhouse gases transform patterns of natural variability, together with substantial socio-economic change, predicates that management of freshwater resources has and will increasingly become a critical task (Famiglietti, 2014). In a climate where it is broadly predicted that “wet gets wetter, dry gets drier” (Trenberth, 2011), water storage at and below the land surface will be a vital tool in enabling successful adaptation to the changing global environment (Damkjaer and Taylor, 2017; Wada, 2016).
Despite the importance of groundwater, there are considerable gaps in current knowledge and understanding (Güntner et al., 2007). Direct observations of groundwater are sparse in relation to its geographical scale so most global or regional groundwater data are based on output from large-scale models. These include global hydrological models (GHMs) (Sood and Smakhtin, 2015) and land surface models (LSMs) (Bierkens, 2015; Overgaard et al., 2006; Wood et al., 2011) for which there are often insufficient data available to constrain or calibrate (Döll et al., 2016). Model simulation of key processes such as soil hydrodynamics and groundwater recharge is therefore based on theoretical frameworks rather than field data (Scanlon et al., 2002). As a result, there is also considerable uncertainty about climate–groundwater dynamics. Recent work in this area has either focused on localised observations of changes in groundwater storage (ΔGWS) from piezometry (Cuthbert et al., 2019a) or occurred adjacent to large centres of population where human intervention, through the extraction of groundwater by pumping, can greatly influence observational measurements (Scanlon et al., 2018). In the context of an ∼85 % increase in global groundwater abstraction from 1979 to 2010 (Wada et al., 2014), an understanding of climate–groundwater dynamics, supported by large-scale observational data, is required to inform sustainable access to groundwater resources (Taylor et al., 2009).
In response to the lack of in situ field observations, remote sensing by satellite is increasingly being utilised to expand the scope of observational data available to Earth Sciences (Acker and Leptoukh, 2007). An important advance in the quality of global data for hydrological studies has come from the Gravity Recovery and Climate Experiment (GRACE), a collaboration between the National Aeronautics and Space Administration (NASA) in the USA and the German Aerospace Centre (DLR) launched in March 2002 (Tapley et al., 2004). Completed sets of approximately monthly measurements are used to derive the changes in mass at the Earth's surface, and from these data mass fluxes can be extracted that directly relate to the hydrosphere. Over land, the flux is expressed as a change in total water storage (ΔTWS) at a spatial resolution of ∼300 km and with an expected accuracy of better than 2 cm equivalent water height (EWH) (Tapley et al., 2004). GRACE ceased operation due to battery failure in mid-2016 having created a record of 163 monthly gravity solutions (Tapley et al., 2019). Although GRACE operated for 10 years longer than anticipated at its launch, it is a relatively brief dataset in relation to large-scale climate patterns impacting the global hydrological system with frequencies of several years or decades (e.g. Pacific Decadal Oscillation – PDO, Atlantic Multidecadal Oscillation – AMO). Nevertheless, inter-annual periodicities associated with the El Niño–Southern Oscillation (ENSO) and the Antarctic Circumpolar Wave (ACW) have been detected (Mémin et al., 2015; Ni et al., 2018; Phillips et al., 2012).
Intrinsic parameters of GRACE data effectively define the spatial and temporal dimensions of this study, but there are additional constraints related to the derivation of ΔGWS data from GRACE ΔTWS that also need to be considered. The sub-division of GRACE ΔTWS into its component parts, including ΔGWS, requires the application of GHM or LSM output that is itself subject to associated uncertainty, as already noted (Döll et al., 2014). It has been demonstrated that there is a relatively poor correlation between GRACE and GHMs and LSMs in the evaluation of ΔTWS, with significant discrepancies at the basic level of whether storage trends are increasing or decreasing (Scanlon et al., 2018). These findings have been confirmed with reference to regional piezometric groundwater measurements from tropical aquifers in Africa (Bonsor et al., 2018). Thus, the application of GRACE data to ΔGWS implies three distinct areas of uncertainty: in the processing of the GRACE signal, accuracy of GHM and LSM model projections and mutual consistency of the observed (GRACE) and modelled (GHM and LSM) data (Long et al., 2015).
This study investigates the spatio-temporal properties of climate–groundwater dynamics using a subset of the 37 large aquifer systems of the world (LASW) as defined by the Worldwide Hydrogeological Mapping and Assessment Programme (WHYMAP) (Anon, 2008) and shown in Fig. S1 in the Supplement. This subset comprises aquifers that lie broadly within the tropics and sub-tropics where climate variability is mostly defined by rainfall (Shepherd, 2014). The 14 aquifers selected are listed in Table 1, together with their key characteristics including aridity index (AI) calculated from the Consultative Group for International Agriculture Research's Consortium for Spatial Information (CGIAR-CSI) Global Aridity Index dataset (Trabucco and Zomer, 2019) shown in Fig. 1. Following the work of Shamsudduha and Taylor (2020), the groundwater storage response to regional climate variability for these 14 large-scale aquifer systems is investigated using ΔGWS data extracted from the whole of the available GRACE ΔTWS time series (August 2002–July 2016), together with climate data that are defined by the areal extent of each of the aquifer systems.
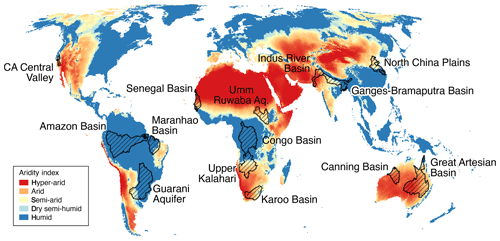
Figure 1The 14 selected world large-scale aquifers (the study aquifers) overlaid on the CGIAR-CSI Global Aridity Index dataset (Trabucco and Zomer, 2019).
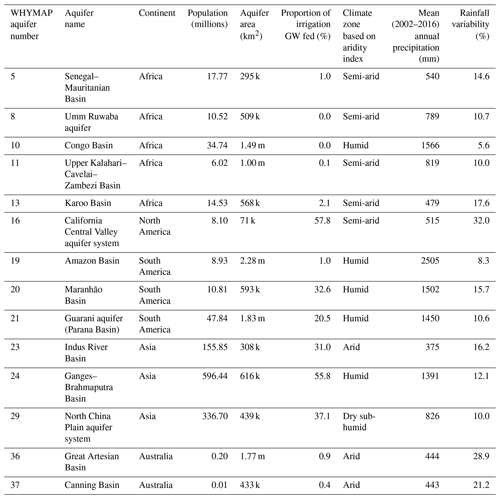
Table 1Characteristics of the 14 aquifer systems selected for the study according to the WHYMAP and CGIAR-CSI databases with statistics giving (L to R): total number of resident population, aquifer area, proportion of groundwater-fed irrigation, mean aridity index classification (Trabucco and Zomer, 2019), mean annual rainfall and mean variability in annual rainfall.
Several studies have used GRACE data to examine storage changes within a particular groundwater (GW) system (e.g. Becker et al., 2010; Bonsor et al., 2018; Chen et al., 2010, 2016; Henry et al., 2011; Z. Huang et al., 2015; Ramillien et al., 2014; Shamsudduha et al., 2012, 2017; Tiwari et al., 2009; Xavier et al., 2010; Yeh et al., 2006). Here, we examine the dynamics of climate–groundwater interactions inferred from the underlying patterns of large-scale ΔGWS in response to extremes of precipitation. We find that hydraulic memory (HM) is a key component in the classification of groundwater responses to climate variability. We then seek to reconcile the results with reference to the physical characteristics of individual aquifer systems (Cuthbert et al., 2019b) whilst accounting for anomalous responses in ΔGWS to climate variability.
2.1 GWS derived from GRACE data
Mass fluxes relating to the hydrosphere contained in the GRACE land-signal measurement of changes in the Earth's gravitational field are defined as ΔTWS. In order to obtain information relating specifically to groundwater, this signal is separated into the component parts that comprise TWS, generally represented as
where SWS is surface water storage, SMS is soil moisture storage and SNS is snow-water equivalent storage. ΔGWS is then derived from ΔTWS according to the following equation:
The locations of the 14 aquifers are outside areas where changes in snow-water equivalent substantially impact ΔTWS (Getirana et al., 2017). ΔSNS can consequently be omitted so that Eq. (2) can be rewritten for the purposes of this particular study as
Since GRACE started transmitting, several solutions have been developed for analysing and producing GRACE ΔTWS data to increasing levels of accuracy with the intention that the data be readily and freely available for research (Landerer and Swenson, 2012). In this instance, three different products were drawn from Shamsudduha and Taylor (2020), two of which are spherical harmonic (SH) solutions comprising CSR Land (version RL05.DSTvSCS1409) from the Centre for Space Research (CSR) at the University of Texas at Austin and CNES/GRGS (version RL03-v1) from the French Centre National d’Etudes Spatiale (CNES) and the Groupe de Recherche de Géodésie Spatiale (GRGS) and one of which is JPL-mascon (version RL05M 1.MSCNv01) from the Jet Propulsion Laboratory (JPL) NASA. To derive ΔTWS, all GRACE solutions require additional processing that includes corrections for glacial isostatic rebound and atmospheric mass variation (Landerer and Swenson, 2012). SH solutions also require spatial filtering (or “de-striping”), whereas JPL-mascon does not as it directly converts the GRACE signal into mass concentration blocks (mascons), rendering monthly gravitational fields directly as 3∘ × 3∘ gridded spatial components to reduce errors (Watkins et al., 2015).
On inspection, the divergence between the three ΔTWS datasets was significant when summed over the time series. The relatively large coefficient of variance, −104 %, even though derived from a small sample size, calls into question the use of an ensemble mean for this study. Such an approach may be appropriate for the use of SH products alone (Sakumura et al., 2014), but it is preferable not to combine SH products and mascons (Felix W. Landerer, personal communication, 2019). Consequently we rely solely on the JPL-mascon dataset possessing a better signal-to-noise ratio and potentially less error (Scanlon et al., 2016; Watkins et al., 2015; Xie et al., 2018). The employed JPL-mascon dataset has been spatially sampled at a 0.5∘ grid using dimensionless scaling factors provided as 0.5∘ × 0.5∘ bins derived from the CLM4.0 LSM (Long et al., 2015; Wiese et al., 2016). GRACE ΔTWS is not a time-invariant measure (Wahr et al., 1998), and in the standard datasets all anomalies are given with respect to a baseline which is the mean over the period January 2004 to December 2009 (JPL NASA, 2019). However, we examine the completed available GRACE ΔTWS time series with respect to climate anomalies over the consistent timeframe of the entire series. Consequently, the employed JPL-mascon ΔTWS dataset has been rescaled with respect to a time mean taken over the whole period of GRACE operation (August 2002–July 2016), which is the study reference period (SRP) (JPL NASA, 2019).
As set out in Eq. (3), datasets for ΔSMS and ΔSWS derived from LSMs are required to determine ΔGWS from ΔTWS since observational data at the spatio-temporal scales of this study do not exist. Datasets for the 14 aquifer systems were drawn from NASA's Global Land Data Assimilation System (GLDAS) (Rodell et al., 2004) comprising the output from four different LSMs (Shamsudduha and Taylor, 2020): the Common (Community) Land Model (CLM, version 2.0), Noah (version 2.7.1), the Variable Infiltration Capacity (VIC) model (version 1.0) and Mosaic (version 1.0) (Rui and Beaudoing, 2019). As with ΔTWS, analysis of the four LSM datasets for ΔSWS + ΔSMS shows that their divergence summed over the entire time series is substantial, with a coefficient of variance of 258 %, suggesting that a LSM-ensemble mean approach may also not be appropriate for this analysis even given the restricted sample size. Further, the inter- and intra-model variability of ΔSWS in the LSM datasets , assessed as surface runoff (e.g. Shamsudduha and Taylor, 2020; Thomas et al., 2017), is much less substantial than that of ΔSMS (inter-model coefficient of variance 378 %). In the absence of consideration of ΔSWS, groundwater recharge is primarily determined by the effect of evapotranspiration on moisture in the soil zone (Long and Mahler, 2013). Therefore, for this study, the modelling of ΔSMS is a key determinant of the outcomes for ΔGWS computed using Eq. (3) (de Vries and Simmers, 2002). Modelled soil profiles vary substantially in each of the four LSMs ranging in depth from 3.5 m (Mosaic) to 1.9 m (VIC) and, in vertical layers, from 10 m (CLM) to 3 m (VIC & Mosaic) (Rodell et al., 2004). CLM 2.0 (Bonan et al., 2002; Dai et al., 2003), with 3.4 m depth and 10 vertical layers, features the most well-developed soil model (Scanlon et al., 2018) and has been shown to perform well in comparative testing (Scanlon et al., 2018; Spennemann et al., 2014). In addition, CLM has demonstrated appropriate variability in initial ensemble model runs undertaken here, meaning that ΔSMS is almost always less than the magnitude of ΔTWS, thereby ensuring that ΔGWS estimates derived from Eq. (3) are not arbitrarily high or low (Shamsudduha and Taylor, 2020). Therefore, this study employs a single model, CLM, for ΔSMS and ΔSWS rather than adopting a LSM ensemble mean approach.
2.2 Climatology
Individual aquifer system shapefiles from the WHYMAP LASW were prepared as ASCII files and uploaded to KNMI Climate Explorer (KNMI Climate Explorer, 2018). This allowed a range of climate data to be extracted for the precise spatial boundaries of each system. In particular, precipitation (PCP) data from the CRU TS4.03 dataset at 0.5∘ resolution (Climate Research Unit, University of East Anglia, 2019) were obtained, together with anomalies (PCPA) normalised for the SRP (2002–2016). The CRU TS4.03 datasets, together with the ΔGWS derived from JPL-mascon ΔTWS and CLM 2.0 ΔSMS and ΔSWS, in accordance with Eq. (3), were used to create time series analyses to explore correlations over different time and volume components through integration. In this respect, the use of “annual” in this study implies the appropriate hydrological year (HY).
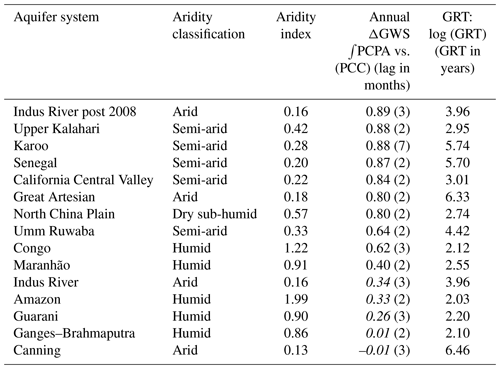
In order to calibrate the time series for each aquifer system prior to further analysis, the lag between monthly PCP, as the primary climate–groundwater index, and monthly GRACE ΔTWS was set by maximising the Pearson correlation coefficient (PCC) between the two datasets, validated by point-wise verification of alignment of the time series. In the majority of cases, this comparison showed ΔTWS lagging PCP by 2 months. The lag for the PCPA time series were set in the same way with relation to ΔGWS but with the already determined PCP time series lag set as a minimum. In the case of all aquifer systems except for the Congo, Canning and Indus River basins, this procedure resulted in a consistent lag being applied to all of the time series investigations of each aquifer. Initial investigations also established that only relatively weak first-order correlations exist between ΔTWS and other monthly observational climate data such as the self-calibrating Palmer Drought Severity Index (PDSI-sc) (Wells et al., 2004) and mean temperature anomalies (CPC GHCN/CAMS t2m analysis) (Fan and van den Dool, 2008). By a comparison with both these measures, it appeared that PCPA carried a stronger climate variability signal due to the tropical or sub-tropical location of the selected aquifers (Allan et al., 2010; Shepherd, 2014). An analysis was then conducted to test for correlations between ΔGWS and a series of measures of precipitation. Three separate time series of precipitation were developed to examine the temporal response of the study LASW with respect to the process by which precipitation at the land surface contributes to ΔGWS.
-
PCP equals monthly precipitation.
-
PCPA equals monthly precipitation anomalies with respect to the consistently applied study reference period time-mean baseline, 2002–2016.
-
∫PCPA equals cumulative monthly rainfall anomalies derived by integrating the PCPA time series.
These monthly series were also summed to provide annual time series for each aquifer system. Correlation was measured using the PCC with statistical significance determined by a t test with α=0.05 (Spearman, 1904). In addition, as previously stated, the CGIAR-CSI Global Aridity Index dataset (Trabucco and Zomer, 2019) was obtained, and a numerical AI for each aquifer was extracted as a spatial mean value using quantum geographic information system (QGIS). AI was used to place each aquifer into the climate zone classification specified by the dataset as set out in Table 1. Of the climate zones relating to the 14 aquifer systems, three are arid, five are semi-arid and one is dry semi-humid, giving nine in total in dryland zones (Corvalán et al., 2005), and five are humid.
2.3 Hydraulic memory
In using cumulative rainfall anomalies, this study invokes the concept of system memory (Weber and Stewart, 2004). Several studies have considered the question of hydraulic or hydrologic memory, as it impacts both soil moisture, including land–atmosphere dynamics (Castro et al., 2009; Lo and Famiglietti, 2010; Wu et al., 2002), and groundwater (Currell et al., 2016; Cuthbert et al., 2019b; Güntner et al., 2007; Rodell and Famiglietti, 2001). Central to the definition of this “memory” is that it represents the time taken for a system to re-equilibrate following a change in boundary conditions (Downing et al., 1974). In the case of an aquifer system, approximated to a one-dimensional flow of uniform diffusivity, the groundwater response time (GRT) is given by Eq. (4):
where L is a measure of the scale of the system, S is the storativity, β is a dimensionless constant and T is transmissivity. Qualitatively, Eq. (4) implies that long response times are characterised by large-scale systems and/or low hydraulic diffusivity (i.e. combination of high S and low T) (e.g. Kooi and Groen, 2003). An alternative approach to quantifying memory may be needed in more complex – and realistic – multidimensional flow situations (see Cuthbert et al., 2019b). Nevertheless, Eq. (4) still provides a useful order of magnitude approximation. Here, it is helpful to consider the response time as a delay between system input and system output whereby the output state H, at time t, is given by
where p(τ) is the input state or function at time τ, (t−τ) is the delay between output and input, and θ is an impulse response function (IRF), also known as a transfer function (Long and Mahler, 2013). The IRF is a multi-parameter function that is intended to model the properties of the system so that the output of the IRF determines the time t at which the state H is reached. The hydraulic memory is quantified by the length of time that the effect of the input persists in the system. As the IRF is commonly exponential, making the equilibrium state asymptotic, system memory can be defined as the time interval at which the IRF is 95 % complete. This approach has been successfully applied to modelling aquifer responses to precipitation validated by piezometry in both the USA (Long and Mahler, 2013) and the Netherlands (von Asmuth and Knotters, 2004). Alternatively, system memory may be defined as the length of time taken for the effect of the anomalous input to decay to 1∕e of its starting value when this can be explicitly measured (Cuthbert et al., 2019b; Lo and Famiglietti, 2010). In relation to Eq. (5), chosen precipitation measures are p(τ) input functions, and ΔGWS represents H(t), the output measure. The time step τ for each of the precipitation time series used is as shown in Table 2. Correlation between ΔGWS (output) and a particular precipitation dataset (input) can be considered to be a measure of the persistence of the effect of that input integrated over the time step. The degree of correlation between ΔGWS and annual ∫PCPA is thus indicative of the duration of HM in the aquifer system.
2.4 Regional-scale hydrogeology
In an exploration of climate–groundwater dynamics using GRACE data, the lack of direct physical observational data means that it is necessary to demonstrate that results are not simply artefacts of modelling and signal processing (Rodell et al., 2009). The role of hydrogeology in determining groundwater dynamics is widely acknowledged (Befus et al., 2017; Cuthbert et al., 2019b; de Vries and Simmers, 2002; van Lanen et al., 2013). Here, we seek to validate results inferred from GRACE data with reference to the physical characteristics of specific aquifer systems. In order to categorise the hydrogeology of each aquifer system, a number of available global datasets were sourced as raster files and interrogated in QGIS using the aquifer vector files from WHYMAP LASW. Examined datasets include the following:
-
groundwater response time (GRT) (Cuthbert et al., 2019b);
-
hydraulic conductivity (K) and porosity (Φ) GHLYMPS high-resolution maps (Gleeson et al., 2014);
-
water table depth (WTD) (Fan et al., 2013).
As defined above, the GRT is a temporal measure of the latency of aquifer systems that is derived from their scale and physical properties via Eq. (4). This measure relies on the other datasets listed for its calculation (Cuthbert et al., 2019b). K and Φ are high-resolution datasets derived from recently developed lithological maps of the Earth's surface (Hartmann and Moosdorf, 2012) and their computation uses established geological parameters (Gleeson et al., 2014). However, K is based on permeability mapping from hydrolithologies that have a standard deviation of ∼2 orders of magnitude (Gleeson et al., 2011), and this variance underlies the uncertainty in each of these datasets used. WTD is a 30 arcsec (∼1 km) resolution dataset compiled from available observational data extended by modelled interpolation with both of these data sources being subject to considerable sampling bias and model uncertainty respectively (Fan et al., 2013). All of these datasets are global and derived from combinations of observations and modelled data.
The main results for each aquifer system are given as a monthly time series of ΔTWS and ΔGWS vs. PCP and an annual time series of ΔGWS vs. PCPA and ∫PCPA, shown as Fig. 2a–r for dryland systems and Fig. 3a–j for humid systems. The outcomes are summarised in Table 3. As a general result, all time series plots show a qualitative relationship between ΔGWS and PCP that exhibits interesting and potentially important spatio-temporal variations. The quantitative results show that for ΔGWS there is a strong correlation with annual ∫PCPA for aquifer systems in dryland environments, whereas in humid environments, the strongest correlation is with monthly PCP. Three aquifers – Guarani aquifer, Indus River Basin and Canning Basin – do not follow this general classification, and anomalies are discussed further in Sect. 4.3 below and in the Supplement.

Figure 2Monthly ΔTWS and ΔGWS vs. PCP and annual ΔGWS vs. ∫PCPA time series for each of the dryland climate zone aquifer systems, as labelled. Systems are ordered by decreasing PCC for annual ΔGWS vs. ∫PCPA. All time series are plotted to the aquifer system lag as set out in Table 3, where ΔTWS (ΔGWS) lags PCP (PCPA) by the specified number of months. Y-axis units are equivalent water height (EWH) in centimetres. Note the variation in the y-axis scales. Seven of the annual ∫PCPA data series have been scaled by a factor of 10 for clarity where indicated.
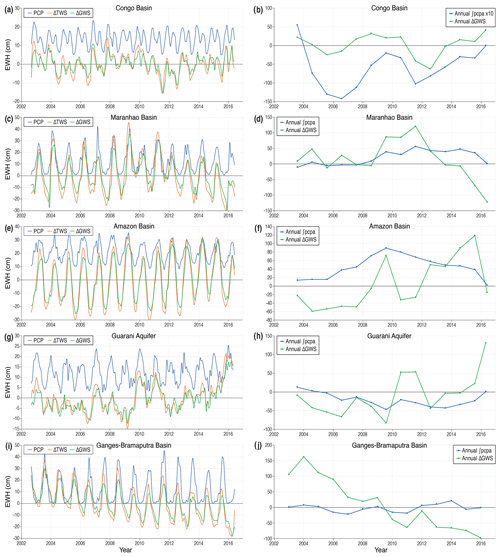
Figure 3Monthly ΔTWS and ΔGWS vs. PCP and annual ΔGWS vs. ∫PCPA time series for each of the humid climate zone aquifer systems, as labelled. Systems are ordered by decreasing PCC for annual ΔGWS vs. ∫PCPA. All time series are plotted to the aquifer system lag as set out in Table 3, where ΔTWS lags PCP by the specified number of months. Y-axis units are equivalent water height (EWH) in centimetres. Note the variation in the y-axis scales. The Congo Basin annual ∫PCPA data series has been scaled by a factor of 10 for clarity.
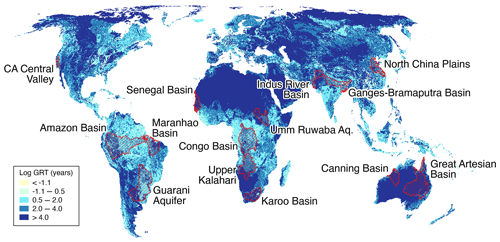
Figure 4The 14 selected world large-scale aquifers (the study aquifers) overlaid on the GRT dataset (original dataset from Cuthbert et al., 2019b).
GRT, shown in Fig. 4, is a measure of the time it takes for an aquifer system to equilibrate after a change in boundary conditions, as discussed above. For the 14 studied aquifers, it extends from centennial to millennial timescales as indicated from median values reported in Tables 4 and S1 (in the Supplement). For humid aquifers, GRT ranges from 100 to 350 years, whereas for dryland systems GRT then escalates to values well in excess of 1,000 years for semi-arid and arid basins; the sub-humid North China Plain aquifer has a GRT of ∼550 years. This order of magnitude point of transition can be identified as the threshold between sensitive (rapid) and insensitive (slow) aquifer response times (Cuthbert et al., 2019b), which show a broad global relationship with aridity. This observation helps to explain groundwater storage responses to climate variability through the memory of the aquifer system defined by both physical characteristics and geographical location. The role of HM is discussed further in Sect. 4.1.
Table 3Summary table of results from monthly and annual time series and aridity datasets. Summary of all correlation results from time series datasets (Pearson correlation coefficient and lag in months in parentheses) and the aridity indices derived from the CGIAR-CSI Global Aridity Index dataset (Trabucco and Zomer, 2019). ΔGWS trend over SRP also shown. Results in italics fall below the t-test threshold. Aquifers are ranked in order of Pearson correlation coefficient for annual ∫PCPA vs. ΔGWS. For each aquifer system, the strongest ΔGWS correlation with PCP or PCPA is shown in bold. Truncated time series results shown for two systems.
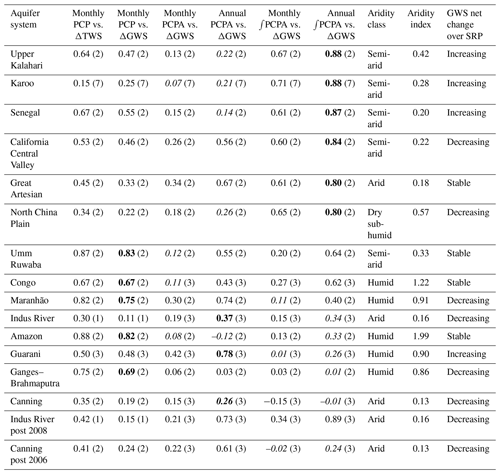
Table 4Relationship between aridity index, climate and regional-scale hydrogeology: data linking climate and regional-scale hydrogeology to GW dynamics. Italicised results fall below t-test threshold.
Presented results represent the outcome of a detailed analysis of the available datasets and, as such, contain important assumptions that need to be acknowledged here. Firstly, the allocation of lag time has been done on a “best fit to the ΔTWS data” basis. It is therefore not derived from analysis of intrinsic physical characteristics of the aquifer systems but is consistent with the range of theoretical values derived from hydrodynamic first principles that anticipate a maximum lag time of 3 months for systems with a large GRT (Townley, 1995), as has been observed by Ahmed et al. (2011). Time lags have been tested for consistency through the alignment of specific events in the various time series (von Storch and Zwiers, 2001). The evident anomaly of a 7-month lag time for the Karoo Basin is discussed in the Supplement. Secondly, the restricted duration of the GRACE dataset should be acknowledged, particularly with regard to the annual time series. In mitigation, statistical significance appears to be robust when tested using the methods described by Zwiers and von Storch (Zwiers and von Storch, 1995), and the use of PCPA and ∫PCPA datasets is designed to minimise the effect of seasonal climate and short-term trends in ΔGWS (Craddock, 1965). Thirdly, the use of Eq. (3) to derive ΔGWS from GRACE ΔTWS data represents a temporal and spatial approximation in representing sub-surface hydrological processes. Simply put, all water below the soil zone neither necessarily comprises GWS nor will it all eventually reach GWS due to lateral flow processes. However, on the scale of the aquifer systems considered here, the use of Eq. (3) is a reasonable approximation (de Vries and Simmers, 2002).
4.1 Role of hydraulic memory
A key finding of this study is that GRACE-derived ΔGWS correlates most strongly with annual ∫PCPA for large-scale aquifers in dryland environments of the tropics and sub-tropics, whereas GRACE-derived ΔGWS correlates most strongly with monthly PCP in humid environments at these latitudes. Further, we show that there is correspondence between the annual ∫PCPA vs. ΔGWS correlations and GRTs of large-scale aquifer systems (Table 4); the latter is a measure derived in accordance with Eq. (4) (Cuthbert et al., 2019b). HM ultimately derives from the physical properties of the saturated portion of the aquifer system (Townley, 1995), and system memory as measured by Eq. (5) is representative of the physical properties of an aquifer system and its climate. Von Asmuth and Knotters (2004) use four parameters to describe groundwater dynamics in their transfer function (τ in Eq. 5) that they argue represents a more accurate description of the physical system than previously used parametric methods (von Asmuth and Knotters, 2004). Further, their description of groundwater dynamics is capable of accommodating non-stationary elements such as climate change and groundwater abstraction (von Asmuth and Knotters, 2004). HM as measured by Eq. (5) is therefore representative of both spatial and temporal variability in aquifer systems, but HM itself can vary spatio-temporally. Indeed the response time to a given boundary change can vary according to the physical circumstances, with persistence lasting from months to hundreds of thousands of years (Cuthbert et al., 2019b).
In this study, the GRACE dataset is not long enough to allow detailed IRF modelling of aquifer systems based on ΔGWS data, which would require an observational record longer than the system memory (Long and Mahler, 2013). An extended GRACE series, together with reduced uncertainty in the permeability dataset from which GRT is derived, may generate closer numerical matches between GRT (Eq. 4) and HM as measured by the method of this study (Eq. 5). Nevertheless, we show that aquifer responses to anomalous precipitation, discussed below, exhibit long HM in dryland environments and relatively short HM in humid environments. The correspondence with GRT extends the classification to two broad categories: dryland environment/long HM/slow GRT and humid environment/short HM/rapid GRT. Note that these categories represent a simplification of the correspondence between HM derived from the study datasets and GRT, which in fact exhibits a spectrum in which Umm Ruwaba (dryland), Congo Basin and Maranhão (both humid) occupy an intermediate position in terms of the correlation between ΔGWS and annual ∫PCPA, as can be seen in Table 3. Aquifers in humid environments, with the exception of the Congo Basin, generally exhibit less HM in this study than expected from GRT values. These humid aquifers, as can be seen in Fig. 4, have some of their area with GRTs in the order of years to tens of years, perhaps meaning that a disproportionate amount of groundwater processes may be moving through these lower GRT areas. This may explain why humid regions have less HM overall than is implied by their median GRT.
4.2 Aquifer responses to anomalous precipitation
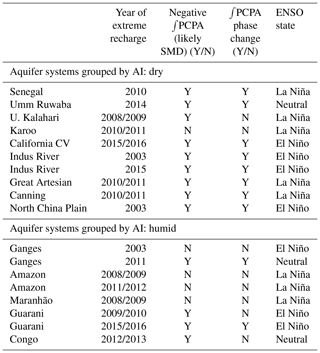
The annual time series of ΔGWS vs. ∫PCPA for each aquifer have been examined to identify years in which the maximum annual increase in ΔGWS occurred, as identified by the steepest positive gradient of the ΔGWS line (Table 5). These years of extreme recharge, inferred from the increase in ΔGWS, are then further categorised by whether (1) prior to the event ∫PCPA was negative, indicating anomalously dry conditions when soil moisture deficits (SMDs) are likely to be widespread, and (2) the ∫PCPA is concurrently shifting from a negative to positive cumulative anomaly associated with an extreme rainfall event. Finally, the NINO3.4 index for 2002–2016 (B. Huang et al., 2015) has been examined (KNMI Climate Explorer, 2018) to indicate the state of ENSO, the dominant control on equatorial precipitation, at the time of the recharge. Nearly all recharge events in dryland aquifer systems take place at a time of negative ∫PCPA (likely SMD) with most coinciding with extreme rainfall as recently observed in a pan-African study by Cuthbert et al. (2019a). Extreme recharge events also generally coincide with El Niño and La Niña events indicating an association with large-scale modes of climate variability identified previously in tropical Africa (Kolusu et al., 2019; Taylor et al., 2013a, b). In contrast, extreme recharge in humid aquifer systems is not consistently associated with either negative ∫PCPA (likely SMD) or anomalous rainfall, though the latter is correlated with ENSO state.
Table 5Aquifer systems grouped by AI – dry (upper) and humid (lower). Extreme recharge years identified from annual time series by slope of ΔGWS plotted line. SMD status inferred by prior negative ∫PCPA and annual ∫PCPA phase change also derived from the same time series. ENSO state from NINO3.4 Index (B. Huang et al., 2015).
4.3 Anomalous trends in groundwater storage
Over the SRP determined by the availability of GRACE data, six aquifer systems show a net decline in groundwater storage: California Central Valley, North China Plain, and the Maranhão, Ganges, Indus and Canning basins. Of these, two aquifer systems (Indus River and Canning basins) do not show a strong correlation between ΔGWS and any of the precipitation data series. Table 4 shows that these same two aquifers do not fit the general classification of the 14 aquifer systems into either dryland/slow GRT/long HM or humid/rapid GRT/short HM systems. These anomalous characteristics may reflect groundwater storage decline through the escalation of groundwater abstraction referenced previously (Wada et al., 2014), and this hypothesis was tested through further analysis as follows below and in further detail in the Supplement.
The Indus River and Canning basins superficially present similar stories of groundwater storage decline, yet contextual analysis of their respective GRACE/CLM ΔGWS datasets reveals two quite different realities. The Indus River Basin supports a population of ∼210 million people (Immerzeel et al., 2010), and its hydrology is strongly influenced by water supply from upstream of the basin, much of it intended for irrigation (Immerzeel et al., 2010). Surface water is augmented by groundwater abstraction, which supplies ∼31 % of the total irrigation demand, but it has been estimated that ∼84 % of the groundwater abstracted returns to the aquifer system as leakage from canals and intensively irrigated fields (Cheema et al., 2014). A net calculation of these effects on ΔGWS, which is detailed in the Supplement, shows that the underlying climate–groundwater dynamics are consistent with the GRT derived from the regional-scale hydrogeology of the aquifer system. In contrast, the Canning Basin is sparsely populated and is not a centre of agriculture (Richey et al., 2015). It is, however, a source of freshwater for iron-ore extraction in adjacent areas (Western Australia Department of Water, 2011), and very little of the abstracted groundwater is returned to the aquifer system as its use in mining causes it to become contaminated (Western Australia Department of Water, 2013). This contaminated groundwater is subsequently disposed in the sea or evaporation ponds (Prosser et al., 2011). The Canning Basin has a very slow GRT and, situated in an arid environment, is subject to low rates of groundwater recharge so that the physically sustainable rate of groundwater abstraction is expected to be very low (Scanlon et al., 2006). The analysis of the Indus and Canning basins is evidence of how groundwater depletion, which has been reported elsewhere (e.g. Famiglietti, 2014; Rodell et al., 2009), impacts relationships between precipitation and ΔGWS.
Strong correlations are found between GRACE-derived annual ΔGWS and ∫PCPA for large-scale aquifer systems in dryland environments. This correlation is much weaker for large-scale aquifer systems in humid zones where a stronger correlation generally exists between monthly ΔGWS and monthly PCP. We propose that the correlation between annual ΔGWS and ∫PCPA demonstrates the existence of hydraulic memory which is central to large-scale climate–groundwater dynamics. For the studied aquifer systems, the measure of correlation between annual ΔGWS and ∫PCPA also shows very good correspondence with the groundwater response time, a measure of the hydraulic memory of an aquifer system derived from its regional-scale hydrogeological and catchment properties (Cuthbert et al., 2019a). The 14 aquifer systems can be broadly categorised into two groups with each group listed in ascending order of groundwater response time:
-
Group 1: dryland/long HM/slow GRT: North China Plain, upper Kalahari Basin, California Central Valley, Umm Ruwaba, and the Indus River, Senegal–Mauritanian, Karoo and Great Artesian (and Canning) basins;
-
Group 2: humid/short HM/rapid GRT: the Amazon, Ganges, Congo, Guarani and Maranhão basins.
Aquifer systems in Group 1 may be less sensitive to seasonal climate variability but also vulnerable to long-term trends from which they will be slow to recover. In contrast, aquifers in Group 2 may be more sensitive to seasonal climate disturbances such as ENSO-related drought but may also be relatively quick to recover. These characteristics can be applied to anticipate the groundwater response to present conditions and to future pressures that can be expected from anthropogenic climate change (Taylor et al., 2013a). The results from the analysis of GRACE data are reconciled to regional-scale hydrogeological conditions, which gives confidence in their validity (Beven and Germann, 2013) albeit with the caveat regarding the uncertainties inherent in all the datasets used (Wilks, 2016).
The new GRACE Follow-On (GRACE-FO) project has now been launched (Frappart and Ramillien, 2018; Tapley et al., 2019), providing an opportunity to augment the existing GRACE ΔTWS dataset without recourse to modelling (Ahmed et al., 2019) and to give greater certainty in linking climate–groundwater dynamics to decadal and longer timescale climate systems including the Pacific Decadal Oscillation and Atlantic Multidecadal Oscillation (Wunsch, 1999). An extended dataset will improve the calibration of HM as it relates to specific aquifer systems, providing a robust context for monitoring ΔGWS, including groundwater decline, in real time and protecting fundamentally important groundwater resources.
Data generated and used in this study can be made available upon request to the corresponding author.
The supplement related to this article is available online at: https://doi.org/10.5194/esd-11-775-2020-supplement.
SO led the analysis of datasets originally compiled by MS and MC, supplemented by datasets developed by SO. RT, CB and MS contributed to the original design of the study with key modifications made by SO. SO drafted the paper with input from RT. All authors contributed to, and commented on, revisions to the submitted paper.
The authors declare that they have no conflict of interest.
Richard G. Taylor and Mohammad Shamsudduha acknowledge support from NERC-ESRC-DFID UPGro GroFutures. Mark O. Cuthbert acknowledges support from a NERC (UK) Independent Research Fellowship.
This research has been supported by the UK NERC-ESRC-DFID (grant no. NE/M008932/1) (UPGro GroFutures) and a NERC (UK) Independent Research Fellowship (grant no. NE/P017819/1).
This paper was edited by Daniel Kirk-Davidoff and reviewed by Bridget Scanlon and one anonymous referee.
Acker, J. G. and Leptoukh, G.: Online analysis enhances use of NASA Earth science data, Eos Trans. Am. Geophys. Union, 88, 14–17, https://doi.org/10.1029/2007EO020003, 2007.
Ahmed, M., Sultan, M., Wahr, J., Yan, E., Milewski, A., Sauck, W., Becker, R., and Welton, B.: Integration of GRACE (Gravity Recovery and Climate Experiment) data with traditional data sets for a better understanding of the time-dependent water partitioning in African watersheds, Geology, 39, 479–482, https://doi.org/10.1130/G31812.1, 2011.
Ahmed, M., Sultan, M., Elbayoumi, T., and Tissot, P.: Forecasting GRACE Data over the African Watersheds Using Artificial Neural Networks, Remote Sens., 11, 1769, https://doi.org/10.3390/rs11151769, 2019.
Allan, R. P., Soden, B. J., John, V. O., Ingram, W., and Good, P.: Current changes in tropical precipitation, Environ. Res. Lett., 5, 025205, https://doi.org/10.1088/1748-9326/5/2/025205, 2010.
Alley, W. M., Healy, R. W., LaBaugh, J. W., and Reilly, T. E.: Flow and Storage in Groundwater Systems, Science, 296, 1985–1990, https://doi.org/10.1126/science.1067123, 2002.
Anon: BGR – WHYMAP – Large Aquifers, available at: https://www.whymap.org/whymap/EN/Maps_Data/Additional_maps/whymap_largeaquifers_g.html (last access: 19 August 2019), 2008.
Becker, M., LLovel, W., Cazenave, A., Güntner, A., and Crétaux, J.-F.: Recent hydrological behavior of the East African great lakes region inferred from GRACE, satellite altimetry and rainfall observations, Comptes Rendus Geoscience, 342, 223–233, https://doi.org/10.1016/j.crte.2009.12.010, 2010.
Befus, K. M., Jasechko, S., Luijendijk, E., Gleeson, T., and Bayani Cardenas, M.: The rapid yet uneven turnover of Earth's groundwater, Geophys. Res. Lett., 44, 5511–5520, https://doi.org/10.1002/2017GL073322, 2017.
Beven, K. and Germann, P.: Macropores and water flow in soils revisited: Review, Water Resour. Res., 49, 3071–3092, https://doi.org/10.1002/wrcr.20156, 2013.
Bierkens, M. F. P.: Global hydrology 2015: State, trends, and directions: Global Hydrology 2015, Water Resour. Res., 51, 4923–4947, https://doi.org/10.1002/2015WR017173, 2015.
Bonan, G. B., Oleson, K. W., Vertenstein, M., Levis, S., Zeng, X., Dai, Y., Dickinson, R. E., and Yang, Z.-L.: The Land Surface Climatology of the Community Land Model Coupled to the NCAR Community Climate Model, J. Climate, 15, 3123–3149, https://doi.org/10.1175/1520-0442(2002)015<3123:TLSCOT>2.0.CO;2, 2002.
Bonsor, H. C., Shamsudduha, M., Marchant, B. P., MacDonald, A. M., and Taylor, R. G.: Seasonal and Decadal Groundwater Changes in African Sedimentary Aquifers Estimated Using GRACE Products and LSMs, Remote Sens., 10, 904, https://doi.org/10.3390/rs10060904, 2018.
Castro, C. L., Beltrán-Przekurat, A. B., and Pielke, R. A.: Spatiotemporal Variability of Precipitation, Modeled Soil Moisture, and Vegetation Greenness in North America within the Recent Observational Record, J. Hydrometeorol., 10, 1355–1378, https://doi.org/10.1175/2009JHM1123.1, 2009.
Cheema, M. J. M., Immerzeel, W. W., and Bastiaanssen, W. G. M.: Spatial Quantification of Groundwater Abstraction in the Irrigated Indus Basin, Groundwater, 52, 25–36, https://doi.org/10.1111/gwat.12027, 2014.
Chen, J. L., Wilson, C. R., and Tapley, B. D.: The 2009 exceptional Amazon flood and interannual terrestrial water storage change observed by GRACE, Water Resour. Res., 46, W12526, https://doi.org/10.1029/2010WR009383, 2010.
Chen, J. L., Wilson, C. R., Tapley, B. D., Scanlon, B., and Güntner, A.: Long-term groundwater storage change in Victoria, Australia from satellite gravity and in situ observations, Global Planet. Change, 139, 56–65, https://doi.org/10.1016/j.gloplacha.2016.01.002, 2016.
Climate Research Unit, University of East Anglia: CRU TS Version 4.01, available at: https://crudata.uea.ac.uk/cru/data/hrg/cru_ts_4.01/, last access: 20 August 2019.
Corvalán, C., Hales, S., McMichael, A. J., Millennium Ecosystem Assessment (Program) and World Health Organization (Eds.): Ecosystems and human well-being: health synthesis, World Health Organization, Geneva, Switzerland, 2005.
Craddock, J. M.: The Analysis of Meteorological Time Series for Use in Forecasting, J. Roy. Stat. Soc. Ser. D, 15, 167–190, https://doi.org/10.2307/2987390, 1965.
Currell, M., Gleeson, T., and Dahlhaus, P.: A New Assessment Framework for Transience in Hydrogeological Systems, Groundwater, 54, 4–14, https://doi.org/10.1111/gwat.12300, 2016.
Cuthbert, M. O., Taylor, R. G., Favreau, G., Todd, M. C., Shamsudduha, M., Villholth, K. G., MacDonald, A. M., Scanlon, B. R., Kotchoni, D. O. V., Vouillamoz, J.-M., Lawson, F. M. A., Adjomayi, P. A., Kashaigili, J., Seddon, D., Sorensen, J. P. R., Ebrahim, G. Y., Owor, M., Nyenje, P. M., Nazoumou, Y., Goni, I., Ousmane, B. I., Sibanda, T., Ascott, M. J., Macdonald, D. M. J., Agyekum, W., Koussoubé, Y., Wanke, H., Kim, H., Wada, Y., Lo, M.-H., Oki, T., and Kukuric, N.: Observed controls on resilience of groundwater to climate variability in sub-Saharan Africa, Nature, 572, 230–234, https://doi.org/10.1038/s41586-019-1441-7, 2019a.
Cuthbert, M. O., Gleeson, T., Moosdorf, N., Befus, K. M., Schneider, A., Hartmann, J., and Lehner, B.: Global patterns and dynamics of climate–groundwater interactions, Nat. Clim. Change, 9, 137–141, https://doi.org/10.1038/s41558-018-0386-4, 2019b.
Dai, Y., Zeng, X., Dickinson, R. E., Baker, I., Bonan, G. B., Bosilovich, M. G., Denning, A. S., Dirmeyer, P. A., Houser, P. R., Niu, G., Oleson, K. W., Schlosser, C. A., and Yang, Z.-L.: The Common Land Model, B. Am. Meteorol. Soc., 84, 1013–1024, https://doi.org/10.1175/BAMS-84-8-1013, 2003.
Damkjaer, S. and Taylor, R.: The measurement of water scarcity: Defining a meaningful indicator, Ambio, 46, 513–531, https://doi.org/10.1007/s13280-017-0912-z, 2017.
de Graaf, I. E. M. , Gleeson, T., van Beek, L. P. H. (Rens), Sutanudjaja, E. H., and Bierkens, M. F. P.: Environmental flow limits to global groundwater pumping, Nature, 574, 90–94, https://doi.org/10.1038/s41586-019-1594-4, 2019.
de Vries, J. J. and Simmers, I.: Groundwater recharge: an overview of processes and challenges, Hydrogeol. J., 10, 5–17, https://doi.org/10.1007/s10040-001-0171-7, 2002.
Döll, P., Hoffmann-Dobrev, H., Portmann, F. T., Siebert, S., Eicker, A., Rodell, M., Strassberg, G., and Scanlon, B. R.: Impact of water withdrawals from groundwater and surface water on continental water storage variations, J. Geodynam., 59–60, 143–156, https://doi.org/10.1016/j.jog.2011.05.001, 2012.
Döll, P., Müller Schmied, H., Schuh, C., Portmann, F. T., and Eicker, A.: Global-scale assessment of groundwater depletion and related groundwater abstractions: Combining hydrological modeling with information from well observations and GRACE satellites, Water Resour. Res., 50, 5698–5720, https://doi.org/10.1002/2014WR015595, 2014.
Döll, P., Douville, H., Güntner, A., Müller Schmied, H., and Wada, Y.: Modelling Freshwater Resources at the Global Scale: Challenges and Prospects, Surv. Geophys., 37, 195–221, https://doi.org/10.1007/s10712-015-9343-1, 2016.
Downing, R. A., Oakes, D. B., Wilkinson, W. B., and Wright, C. E.: Regional development of groundwater resources in combination with surface water, J. Hydrol., 22, 155–177, https://doi.org/10.1016/0022-1694(74)90102-4, 1974.
Famiglietti, J. S.: The global groundwater crisis, Nat. Clim. Change, 4, 945–948, https://doi.org/10.1038/nclimate2425, 2014.
Fan, Y. and van den Dool, H.: A global monthly land surface air temperature analysis for 1948–present, J. Geophys. Res.-Atmos., 113, 1–18, https://doi.org/10.1029/2007JD008470, 2008.
Fan, Y., Li, H., and Miguez-Macho, G.: Global Patterns of Groundwater Table Depth, Science, 339, 940–943, https://doi.org/10.1126/science.1229881, 2013.
Frappart, F. and Ramillien, G.: Monitoring Groundwater Storage Changes Using the Gravity Recovery and Climate Experiment (GRACE) Satellite Mission: A Review, Remote Sens., 10, 829, https://doi.org/10.3390/rs10060829, 2018.
Getirana, A., Kumar, S., Girotto, M., and Rodell, M.: Rivers and Floodplains as Key Components of Global Terrestrial Water Storage Variability, Geophys. Res. Lett., 44, 10359–10368, https://doi.org/10.1002/2017GL074684, 2017.
Gleeson, T., Smith, L., Moosdorf, N., Hartmann, J., Dürr, H. H., Manning, A. H., van Beek, L. P. H., and Jellinek, A. M.: Mapping permeability over the surface of the Earth, Geophys. Res. Lett., 38, L02401, https://doi.org/10.1029/2010GL045565, 2011.
Gleeson, T., Moosdorf, N., Hartmann, J., and van Beek, L. P. H.: A glimpse beneath earth's surface: GLobal HYdrogeology MaPS (GLHYMPS) of permeability and porosity, Geophys. Res. Lett., 41, 3891–3898, https://doi.org/10.1002/2014GL059856, 2014.
Güntner, A., Stuck, J., Werth, S., Döll, P., Verzano, K., and Merz, B.: A global analysis of temporal and spatial variations in continental water storage, Water Resour. Res., 43, W05416, https://doi.org/10.1029/2006WR005247, 2007.
Hartmann, J. and Moosdorf, N.: The new global lithological map database GLiM: A representation of rock properties at the Earth surface, Geochem. Geophy. Geosy., 13, Q12004, https://doi.org/10.1029/2012GC004370, 2012.
Henry, C. M., Allen, D. M., and Huang, J.: Groundwater storage variability and annual recharge using well-hydrograph and GRACE satellite data, Hydrogeol. J., 19, 741–755, https://doi.org/10.1007/s10040-011-0724-3, 2011.
Huang, B., Banzon, V. F., Freeman, E., Lawrimore, J., Liu, W., Peterson, T. C., Smith, T. M., Thorne, P. W., Woodruff, S. D., and Zhang, H.-M.: Extended Reconstructed Sea Surface Temperature (ERSST), Version 4, NOAA National Centers for Environmental Information, https://doi.org/10.7289/v5kd1vvf, 2015.
Huang, Z., Pan, Y., Gong, H., Yeh, P. J.-F., Li, X., Zhou, D., and Zhao, W.: Subregional-scale groundwater depletion detected by GRACE for both shallow and deep aquifers in North China Plain, Geophys. Res. Lett., 42, 1791–1799, https://doi.org/10.1002/2014GL062498, 2015.
Immerzeel, W. W., van Beek, L. P. H., and Bierkens, M. F. P.: Climate Change Will Affect the Asian Water Towers, Science, 328, 1382–1385, https://doi.org/10.1126/science.1183188, 2010.
JPL NASA: Frequently Asked Questions | About, GRACE Tellus, available at: https://grace.jpl.nasa.gov/about/faq, last access: 20 August 2019.
KNMI Climate Explorer: Climate Explorer: Starting point, KNMI Climate Explorer, available at: https://climexp.knmi.nl/start.cgi?id=b08c094a879f19247ae5839cc6377977, last access: 22 December 2018.
Kolusu, S. R., Shamsudduha, M., Todd, M. C., Taylor, R. G., Seddon, D., Kashaigili, J. J., Ebrahim, G. Y., Cuthbert, M. O., Sorensen, J. P. R., Villholth, K. G., MacDonald, A. M., and MacLeod, D. A.: The El Niño event of 2015–2016: climate anomalies and their impact on groundwater resources in East and Southern Africa, Hydrol. Earth Syst. Sci., 23, 1751–1762, https://doi.org/10.5194/hess-23-1751-2019, 2019.
Kooi, H. and Groen, J.: Geological processes and the management of groundwater resources in coastal areas, Neth. J. Geosci., 82, 31–40, https://doi.org/10.1017/S0016774600022770, 2003.
Landerer, F. W.: Personal correspondence, email, available at: https://outlook.office.com/owa/?realm=acl.ac.uk&path=/attachmentlightbox, last access: 14 June 2019.
Landerer, F. W. and Swenson, S. C.: Accuracy of scaled GRACE terrestrial water storage estimates, Water Resour. Res., 48, W04531, https://doi.org/10.1029/2011WR011453, 2012.
Lo, M.-H. and Famiglietti, J. S.: Effect of water table dynamics on land surface hydrologic memory, J. Geophys. Res.-Atmos., 115, D22118, https://doi.org/10.1029/2010JD014191, 2010.
Long, A. J. and Mahler, B. J.: Prediction, time variance, and classification of hydraulic response to recharge in two karst aquifers, Hydrol. Earth Syst. Sci., 17, 281–294, https://doi.org/10.5194/hess-17-281-2013, 2013.
Long, D., Longuevergne, L., and Scanlon, B. R.: Global analysis of approaches for deriving total water storage changes from GRACE satellites, Water Resour. Res., 51, 2574–2594, https://doi.org/10.1002/2014WR016853, 2015.
Mémin, A., Flament, T., Alizier, B., Watson, C., and Rémy, F.: Interannual variation of the Antarctic Ice Sheet from a combined analysis of satellite gravimetry and altimetry data, Earth Planet. Sc. Lett., 422, 150–156, https://doi.org/10.1016/j.epsl.2015.03.045, 2015.
Ni, S., Chen, J., Wilson, C. R., Li, J., Hu, X., and Fu, R.: Global Terrestrial Water Storage Changes and Connections to ENSO Events, Geophys., 39, 1–22, https://doi.org/10.1007/s10712-017-9421-7, 2018.
Overgaard, J., Rosbjerg, D., and Butts, M. B.: Land-surface modelling in hydrological perspective – a review, Biogeosciences, 3, 229–241, https://doi.org/10.5194/bg-3-229-2006, 2006.
Phillips, T., Nerem, R. S., Fox-Kemper, B., Famiglietti, J. S., and Rajagopalan, B.: The influence of ENSO on global terrestrial water storage using GRACE, Geophys. Res. Lett., 39, L16705, https://doi.org/10.1029/2012GL052495, 2012.
Prosser, I., Wolf, L., and Littleboy, A.: Water in mining and industry, in: Water: Science and Solutions for Australia, edited by: Prosser, I., CSIRO Publishing, 2011, 135–146, 2011.
Ramillien, G., Frappart, F., and Seoane, L.: Application of the Regional Water Mass Variations from GRACE Satellite Gravimetry to Large-Scale Water Management in Africa, Remote Sens., 6, 7379–7405, https://doi.org/10.3390/rs6087379, 2014.
Richey, A. S., Thomas, B. F., Lo, M.-H., Reager, J. T., Famiglietti, J. S., Voss, K., Swenson, S., and Rodell, M.: Quantifying renewable groundwater stress with GRACE, Water Resour. Res., 51, 5217–5238, https://doi.org/10.1002/2015WR017349, 2015.
Rodell, M. and Famiglietti, J. S.: An analysis of terrestrial water storage variations in Illinois with implications for the Gravity Recovery and Climate Experiment (GRACE), Water Resour. Res., 37, 1327–1339, https://doi.org/10.1029/2000WR900306, 2001.
Rodell, M., Houser, P. R., Jambor, U., Gottschalck, J., Mitchell, K., Meng, C.-J., Arsenault, K., Cosgrove, B., Radakovich, J., Bosilovich, M., Entin, J. K., Walker, J. P., Lohmann, D., and Toll, D.: The Global Land Data Assimilation System, B. Am. Meteorol. Soc., 85, 381–394, https://doi.org/10.1175/BAMS-85-3-381, 2004.
Rodell, M., Velicogna, I., and Famiglietti, J. S.: Satellite-based estimates of groundwater depletion in India, Nature, 460, 999–1002, https://doi.org/10.1038/nature08238, 2009.
Rui, H. and Beaudoing, H.: README Document for GLDAS Version 1 Data Products, NASA Goddard Earth Science Data Information and Services Center (GES DISC) 32 pp., 2019.
Sakumura, C., Bettadpur, S., and Bruinsma, S.: Ensemble prediction and intercomparison analysis of GRACE time-variable gravity field models, Geophys. Res. Lett., 41, 1389–1397, https://doi.org/10.1002/2013GL058632, 2014.
Scanlon, B. R., Healy, R. W., and Cook, P. G.: Choosing appropriate techniques for quantifying groundwater recharge, Hydrogeol. J., 10, 18–39, https://doi.org/10.1007/s10040-001-0176-2, 2002.
Scanlon, B. R., Keese, K. E., Flint, A. L., Flint, L. E., Gaye, C. B., Edmunds, W. M., and Simmers, I.: Global synthesis of groundwater recharge in semiarid and arid regions, Hydrol. Process., 20, 3335–3370, https://doi.org/10.1002/hyp.6335, 2006.
Scanlon, B. R., Zhang, Z., Save, H., Wiese, D. N., Landerer, F. W., Long, D., Longuevergne, L., and Chen, J.: Global evaluation of new GRACE mascon products for hydrologic applications: Global Analysis Of Grace Mascon Products, Water Resour. Res., 52, 9412–9429, https://doi.org/10.1002/2016WR019494, 2016.
Scanlon, B. R., Zhang, Z., Save, H., Sun, A. Y., Schmied, H. M., van Beek, L. P. H., Wiese, D. N., Wada, Y., Long, D., Reedy, R. C., Longuevergne, L., Döll, P., and Bierkens, M. F. P.: Global models underestimate large decadal declining and rising water storage trends relative to GRACE satellite data, P. Natl. Acad. Sci. USA, 115, E1080–E1089, https://doi.org/10.1073/pnas.1704665115, 2018.
Shamsudduha, M. and Taylor, R. G.: Groundwater storage dynamics in the world's large aquifer systems from GRACE: uncertainty and role of extreme precipitation, Earth Syst. Dynam., 11, 755–774, https://doi.org/10.5194/esd-11-755-2020, 2020.
Shamsudduha, M., Taylor, R. G., and Longuevergne, L.: Monitoring groundwater storage changes in the highly seasonal humid tropics: Validation of GRACE measurements in the Bengal Basin, Water Resour. Res., 48, W02508, https://doi.org/10.1029/2011WR010993, 2012.
Shamsudduha, M., Taylor, R. G., Jones, D., Longuevergne, L., Owor, M., and Tindimugaya, C.: Recent changes in terrestrial water storage in the Upper Nile Basin: an evaluation of commonly used gridded GRACE products, available at: https://hal-insu.archives-ouvertes.fr/insu-01590219 (last access: 4 August 2019), 2017.
Shepherd, T. G.: Atmospheric circulation as a source of uncertainty in climate change projections, Nat. Geosci., 7, 703–708, https://doi.org/10.1038/ngeo2253, 2014.
Sood, A. and Smakhtin, V.: Global hydrological models: a review, Hydrolog. Sci. J., 60, 549–565, https://doi.org/10.1080/02626667.2014.950580, 2015.
Spearman, C.: The Proof and Measurement of Association between Two Things, Am. J. Psychol., 15, 72–101, https://doi.org/10.2307/1412159, 1904.
Spennemann, P. C., Rivera, J. A., Saulo, A. C., and Penalba, O. C.: A Comparison of GLDAS Soil Moisture Anomalies against Standardized Precipitation Index and Multisatellite Estimations over South America, J. Hydrometeorol., 16, 158–171, https://doi.org/10.1175/JHM-D-13-0190.1, 2014.
Tapley, B. D., Bettadpur, S., Watkins, M., and Reigber, C.: The gravity recovery and climate experiment: Mission overview and early results, Geophys. Res. Lett., 31, L09607, https://doi.org/10.1029/2004GL019920, 2004.
Tapley, B. D., Watkins, M. M., Flechtner, F., Reigber, C., Bettadpur, S., Rodell, M., Sasgen, I., Famiglietti, J. S., Landerer, F. W., Chambers, D. P., Reager, J. T., Gardner, A. S., Save, H., Ivins, E. R., Swenson, S. C., Boening, C., Dahle, C., Wiese, D. N., Dobslaw, H., Tamisiea, M. E., and Velicogna, I.: Contributions of GRACE to understanding climate change, Nat. Clim. Change, 9, 358–369, https://doi.org/10.1038/s41558-019-0456-2, 2019.
Taylor, R. G., Koussis, A. D., and Tindimugaya, C.: Groundwater and climate in Africa – a review, Hydrolog. Sci. J., 54, 655–664, https://doi.org/10.1623/hysj.54.4.655, 2009.
Taylor, R. G., Scanlon, B., Döll, P., Rodell, M., van Beek, R., Wada, Y., Longuevergne, L., Leblanc, M., Famiglietti, J. S., Edmunds, M., Konikow, L., Green, T. R., Chen, J., Taniguchi, M., Bierkens, M. F. P., MacDonald, A., Fan, Y., Maxwell, R. M., Yechieli, Y., Gurdak, J. J., Allen, D. M., Shamsudduha, M., Hiscock, K., Yeh, P. J.-F., Holman, I., and Treidel, H.: Ground water and climate change, Nat. Clim. Change, 3, 322–329, https://doi.org/10.1038/nclimate1744, 2013a.
Taylor, R. G., Todd, M. C., Kongola, L., Maurice, L., Nahozya, E., Sanga, H., and MacDonald, A. M.: Evidence of the dependence of groundwater resources on extreme rainfall in East Africa, Nat. Clim. Change, 3, 374–378, https://doi.org/10.1038/nclimate1731, 2013b.
Thomas, B. F., Caineta, J., and Nanteza, J.: Global Assessment of Groundwater Sustainability Based On Storage Anomalies, Geophys. Res. Lett., 44, 11445–11455, https://doi.org/10.1002/2017GL076005, 2017.
Tiwari, V. M., Wahr, J., and Swenson, S.: Dwindling groundwater resources in northern India, from satellite gravity observations, Geophys. Res. Lett., 36, L18401, https://doi.org/10.1029/2009GL039401, 2009.
Townley, L. R.: The response of aquifers to periodic forcing, Adv. Water Resour., 18, 125–146, https://doi.org/10.1016/0309-1708(95)00008-7, 1995.
Trabucco, A. and Zomer, R.: Global Aridity Index and Potential Evapotranspiration (ET0) Climate Database v2, Figshare, https://doi.org/10.6084/m9.figshare.7504448.v3, 2019.
Trenberth, K. E.: Changes in precipitation with climate change, Clim. Res., 47, 123–138, https://doi.org/10.3354/cr00953, 2011.
Van Lanen, H. A. J., Wanders, N., Tallaksen, L. M., and Van Loon, A. F.: Hydrological drought across the world: impact of climate and physical catchment structure, Hydrol. Earth Syst. Sci., 17, 1715–1732, https://doi.org/10.5194/hess-17-1715-2013, 2013.
von Asmuth, J. R. and Knotters, M.: Characterising groundwater dynamics based on a system identification approach, J. Hydrol., 296, 118–134, https://doi.org/10.1016/j.jhydrol.2004.03.015, 2004.
von Storch, H. and Zwiers, F. W.: Statistical Analysis in Climate Research, Cambridge University Press, Cambridge, 2001.
Wada, Y.: Modeling Groundwater Depletion at Regional and Global Scales: Present State and Future Prospects, Surv. Geophys., 37, 419–451, https://doi.org/10.1007/s10712-015-9347-x, 2016.
Wada, Y., Wisser, D., and Bierkens, M. F. P.: Global modeling of withdrawal, allocation and consumptive use of surface water and groundwater resources, Earth Syst. Dynam., 5, 15–40, https://doi.org/10.5194/esd-5-15-2014, 2014.
Wahr, J., Molenaar, M., and Bryan, F.: Time variability of the Earth's gravity field: Hydrological and oceanic effects and their possible detection using GRACE, J. Geophys. Res.-Solid, 103, 30205–30229, https://doi.org/10.1029/98JB02844, 1998.
Watkins, M. M., Wiese, D. N., Yuan, D.-N., Boening, C., and Landerer, F. W.: Improved methods for observing Earth's time variable mass distribution with GRACE using spherical cap mascons, J. Geophys. Res.-Solid, 120, 2648–2671, https://doi.org/10.1002/2014JB011547, 2015.
Weber, K. and Stewart, M.: A Critical Analysis of the Cumulative Rainfall Departure Concept, Ground Water, 42, 935–938, 2004.
Wells, N., Goddard, S., and Hayes, M. J.: A Self-Calibrating Palmer Drought Severity Index, J. Climate, 17, 2335–2351, https://doi.org/10.1175/1520-0442(2004)017<2335:ASPDSI>2.0.CO;2, 2004.
Western Australia Department of Water: Capacity of water resources in the Mid west to meet mining and industrial growth: a status report, Dept. of Water, Perth, WA, 2011.
Western Australia Department of Water: Western Australian water in mining guideline, Dept. of Water, Perth, WA, 2013.
Wiese, D. N., Landerer, F. W., and Watkins, M. M.: Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution, Water Resour. Res., 52, 7490–7502, https://doi.org/10.1002/2016WR019344, 2016.
Wilks, D. S.: “The Stippling Shows Statistically Significant Grid Points”: How Research Results are Routinely Overstated and Overinterpreted, and What to Do about It, B. Am. Meteorol. Soc., 97, 2263–2273, https://doi.org/10.1175/BAMS-D-15-00267.1, 2016.
Wood, E. F., Roundy, J. K., Troy, T. J., van Beek, L. P. H., Bierkens, M. F. P., Blyth, E., de Roo, A., Döll, P., Ek, M., Famiglietti, J., Gochis, D., van de Giesen, N., Houser, P., Jaffé, P. R., Kollet, S., Lehner, B., Lettenmaier, D. P., Peters-Lidard, C., Sivapalan, M., Sheffield, J., Wade, A., and Whitehead, P.: Hyperresolution global land surface modeling: Meeting a grand challenge for monitoring Earth's terrestrial water, Water Resour. Res., 47, W05301, https://doi.org/10.1029/2010WR010090, 2011.
Wu, W., Geller, M. A., and Dickinson, R. E.: The Response of Soil Moisture to Long-Term Variability of Precipitation, J. Hydrometeorol., 3, 604–613, https://doi.org/10.1175/1525-7541(2002)003<0604:TROSMT>2.0.CO;2, 2002.
Wunsch, C.: The Interpretation of Short Climate Records, with Comments on the North Atlantic and Southern Oscillations, B. Am. Meteorol. Soc., 80, 245–255, https://doi.org/10.1175/1520-0477(1999)080<0245:TIOSCR>2.0.CO;2, 1999.
Xavier, L., Becker, M., Cazenave, A., Longuevergne, L., Llovel, W., and Filho, O. C. R.: Interannual variability in water storage over 2003–2008 in the Amazon Basin from GRACE space gravimetry, in situ river level and precipitation data, Remote Sens. Environ., 114, 1629–1637, https://doi.org/10.1016/j.rse.2010.02.005, 2010.
Xie, X., Xu, C., Wen, Y., and Li, W.: Monitoring Groundwater Storage Changes in the Loess Plateau Using GRACE Satellite Gravity Data, Hydrological Models and Coal Mining Data, Remote Sens., 10, 605, https://doi.org/10.3390/rs10040605, 2018.
Yeh, P. J.-F., Swenson, S. C., Famiglietti, J. S., and Rodell, M.: Remote sensing of groundwater storage changes in Illinois using the Gravity Recovery and Climate Experiment (GRACE), Water Resour. Res., 42, W12203, https://doi.org/10.1029/2006WR005374, 2006.
Zwiers, F. W. and von Storch, H.: Taking Serial Correlation into Account in Tests of the Mean, J. Climate, 8, 336–351, https://doi.org/10.1175/1520-0442(1995)008<0336:TSCIAI>2.0.CO;2, 1995.






