Synthesis and evaluation of historical meridional heat transport from midlatitudes towards the Arctic

Meridional energy transport (MET), both in the atmosphere (AMET) and ocean (OMET), has significant impact on the climate in the Arctic. In this study, we quantify AMET and OMET at subpolar latitudes from six reanalysis data sets. We investigate the differences between the data sets and we check the coherence between MET and the Arctic climate variability at interannual timescales. The results indicate that, although the mean transport in all data sets agrees well, the spatial distributions and temporal variations of AMET and OMET differ substantially among the reanalysis data sets. For the ocean, only after 2007, the low-frequency signals in all reanalysis products agree well. A further comparison with observed heat transport at 26.5^∘ N and the subpolar Atlantic, and a high-resolution ocean model hindcast confirms that the OMET estimated from the reanalysis data sets are consistent with the observations. For the atmosphere, the differences between ERA-Interim and the Japanese 55-year Reanalysis (JRA-55) are small, while the Modern-Era Retrospective analysis for Research and Applications version 2 (MERRA-2) differs from them. An extended analysis of linkages between Arctic climate variability and AMET shows that atmospheric reanalyses differ substantially from each other. Among the chosen atmospheric products, ERA-Interim and JRA-55 results are most consistent with those from coupled climate models. For the ocean, the Ocean Reanalysis System 4 (ORAS4) and Simple Ocean Data Assimilation version 3 (SODA3) agree well on the relation between OMET and sea ice concentration (SIC), while the GLobal Ocean reanalyses and Simulations version 3 (GLORYS2V3) deviates from those data sets. The regressions of multiple fields in the Arctic on both AMET and OMET suggest that the Arctic climate is sensitive to changes of meridional energy transport at subpolar latitudes in winter. Given the good agreement on the diagnostics among assessed reanalysis products, our study suggests that the reanalysis products are useful for the evaluation of energy transport. However, assessments of products with the AMET and OMET estimated from reanalysis data sets beyond interannual timescales should be conducted with great care and the robustness of results should be evaluated through intercomparison, especially when studying variability and interactions between the Arctic and midlatitudes.

1 Introduction

Poleward meridional energy transport, both in the atmosphere (AMET) and ocean (OMET), is one of the most fundamental aspects of the climate system. It is closely linked to the changes of weather and climate at different latitudes. The quantifications of AMET and OMET have been studied extensively. In the 1980s, many efforts were made to reproduce the AMET and OMET with very limited observational data available (Vonder Haar and Oort, 1973; Oort and Vonder Haar, 1976). After entering the satellite era, much progress has been made in particular during the recent two data-rich decades. Using the radiation at the top of the atmosphere from satellite data and the reanalysis data, a complete picture of AMET and OMET is given by Trenberth and Caron (2001). Following their work, rapid progress was made using similar methodologies and new data sets of observations (Ganachaud and Wunsch, 2000, 2003; Wunsch, 2005; Fasullo and Trenberth, 2008; Zheng and Giese, 2009; Mayer and Haimberger, 2012). Nevertheless, these estimations still suffered from problems like mass imbalance, unrealistic moisture budget, coarse resolution and sparseness of observations (Trenberth, 1991; Trenberth and Solomon, 1994). Fortunately, recent improvements in numerical weather prediction and ocean models, and increased data coverage of observations provide a basis to improve the estimation of AMET and OMET. As a result of an increase of available reanalysis products, an increase in resolution and length of the covered time span and an increase of components of the Earth system that are included in the products (Dee et al., 2011; Gelaro et al., 2017; Harada et al., 2016; Balmaseda et al., 2013; Ferry et al., 2012b; Carton et al., 2018), it is very promising to have better quantification of AMET and OMET using the latest reanalysis data sets. In this study, we will provide further insights into MET from midlatitudes towards the Arctic, with the state-of-the-art reanalysis products.

To support the examination of MET from midlatitudes towards the Arctic, it is worth investigating the AMET and OMET in relation to climate variability at different timescales in the Arctic region. In recent decades, the Arctic has been warming twice as fast as the global average (Comiso and Hall, 2014; Francis et al., 2017). This phenomenon is known as Arctic amplification (AA) and it has an impact far beyond the Arctic (Miller et al., 2010; Serreze and Barry, 2011). In order to understand the warming, the processes behind the AA and its wider consequences, and to make reliable predictions of the Arctic climate, it is crucial to understand Arctic climate variability. Among all factors responsible for the variability in the processes described above, meridional energy transport, from midlatitudes toward the Arctic, plays a significant role (Graversen et al., 2008; Kapsch et al., 2013; Zhang, 2015). There is a large volume of published studies describing the impacts of AMET and OMET on the variation of sea ice and the warming in the Arctic. Using reanalysis data, Yang et al. (2010) showed that poleward AMET is linked with the evolution of temperature in the free troposphere at decadal timescales. By separating the planetary and synoptic-scale waves, Graversen and Burtu (2016) showed that latent heat transport, as a component of AMET, influences the Arctic warming with reanalysis data. Gimeno-Sotelo et al. (2019) studied moisture transport with reanalysis data and observations, and showed that the moisture sources in the Arctic region are linked with interannual fluctuations of Arctic sea ice. Nummelin et al. (2017) analyzed the linkages between OMET, ocean heat content (OHC) and AA through climate model simulations within the Coupled Model Intercomparison Project phase 5 (CMIP5). They reported an enhancement of OMET as a result of heat loss in the subpolar ocean and the contribution of OMET to the AA through increasing OHC in the Arctic Ocean. Also by analyzing CMIP5 simulations, Sandø et al. (2014) showed a large impact of heat transport in the Barents Sea on sea ice loss. However, ocean reanalyses do not show a clear sign of AA in the Arctic OHC increases (Mayer et al., 2016; von Schuckmann et al., 2018; Mayer et al., 2019). Consequently, knowledge on poleward AMET and OMET at subpolar and polar latitudes will aid in the understanding of AA.

Global climate models show compensations between variations in atmospheric and oceanic heat transport at subpolar latitudes and midlatitudes (Outten et al., 2018). This is indicative of positive feedbacks between the ocean and atmosphere, and it has been associated with variations in sea ice by some studies (Van der Swaluw et al., 2007; Jungclaus and Koenigk, 2010; van der Linden et al., 2016). These studies all point to connection between energy transport and variations of the Arctic climate. However, these results are mostly based on numerical model simulations and they tend to differ among these models. In contrast to numerical modeling studies, here we intend to examine AMET and OMET variability and their relation with the Arctic using reanalysis data sets, which are regarded as the best estimates of the historical variability.

In this paper, we quantify AMET and OMET using multiple state-of-the-art reanalysis products. These are representations of the historical state of the atmosphere and ocean optimally combining available observations and numerical simulations using data assimilation techniques. Emphasis is placed on the variation of AMET and OMET from midlatitudes to the Arctic at interannual timescales (∼5 years). Different from earlier studies, we include multiple reanalysis data sets for intercomparison. Independent observations in the Atlantic from the Rapid Climate Change-Meridional Overturning Circulation and Heatflux array (RAPID array) and the Overturning in the Subpolar North Atlantic Program (OSNAP) are included in the comparison. The RAPID array is a trans-basin observing array along 26.5^∘ N in the Atlantic (Johns et al., 2011; McCarthy et al., 2015). It has been in operation since 2004 and provides the volume and heat transport in the Atlantic basin. OSNAP is an ocean observation program designed to provide a continuous record of the trans-basin fluxes of heat, mass and freshwater in the subpolar North Atlantic (Susan Lozier et al., 2017; Lozier et al., 2019). Moreover, a state-of-the-art NEMO-LIM2 1∕12^∘ ocean circulation/sea ice model simulation forced by the Drakkar surface forcing data set version 5.2 (Moat et al., 2016) is also employed in the comparison. Based on the intercomparison of reanalysis data, especially with the independent observation data, we will be able to identify the sources of uncertainty. To support our comparison of AMET and OMET, we also investigate the interactions between oceanic and atmospheric variations and remote responses. The correlations between the variability of AMET and OMET, and the changes in the Arctic climate are compared to literature. This is motivated by previous studies that explain those connections with only numerical models or a single reanalysis data set (Graversen, 2006; Graversen et al., 2008; Van der Swaluw et al., 2007; Jungclaus and Koenigk, 2010; Kapsch et al., 2013).

The paper is organized as follows: Sect. 2 presents the data and our methodology. Results and analysis are given in Sect. 3. It includes AMET and OMET calculated from reanalysis data and an intercomparison of them. The correlation between the variability of AMET and OMET, and the Arctic climate is elaborated upon in detail. Finally, remarks are given in Sect. 4 and conclusions are provided in Sect. 5.

2 Data and methodology

The reanalysis data sets used in this study are introduced in this section. Moreover, the methodology for the quantification of AMET and OMET is also included in this section. The statistical tests performed in this study are elucidated in detail.

2.1 Reanalyses

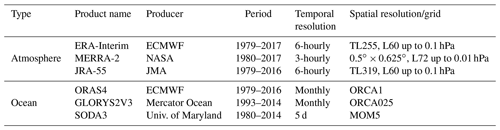
In order to make use of observations and advanced numerical models, six state-of-the-art reanalysis data sets are used in this study. The chosen reanalysis products have a high temporal and spatial resolution; thus, they are suitable for the computation of energy transport (see Sect. 2.3). We chose three atmosphere reanalysis data sets: ERA-Interim, the Modern-Era Retrospective analysis for Research and Applications version 2 (MERRA-2) and the Japanese 55-year Reanalysis (JRA-55) (references below), and three ocean reanalysis data sets: the Ocean Reanalysis System 4 (ORAS4), GLobal Ocean reanalyses and Simulations version 3 (GLORYS2V3) and Simple Ocean Data Assimilation version 3 (SODA3) (references below). To avoid interpolation errors and imbalances in the mass budget introduced by regridding, the calculations are based on data from the original model grid. Note that the latest atmospheric reanalysis (ERA5) from the European Centre for Medium Range Weather Forecasts (ECMWF) is not included here since the model-level data have not been opened to the public yet (ECMWF, 2017). In addition, the computation is too expensive to achieve a longer time series for the study of the interannual variability of AMET using ERA5. As a synthesis, Table 1 shows the basic specifications of the reanalysis products contained in this study.

Table 1 Basic specification of reanalyses products included in this study.

2.1.1 ERA-Interim

ERA-Interim is a global reanalysis data set produced by ECMWF (Dee et al., 2011), which has covered the data-rich period since 1979. It employs cycle 31r2 of ECMWF's Integrated Forecast System (IFS) and generates atmospheric state estimates using a 4D-Var data assimilation with a T255 (∼79 km) horizontal resolution on 60 vertical levels (Berrisford et al., 2009). Compared with its predecessor, ERA-40 (Uppala et al., 2005), ERA-Interim is superior in quality in terms of the atmospheric properties like mass, moisture and energy (Berrisford et al., 2011). The improvement in observations and the ability of 4D-Var contributes a lot to the quality of the divergent wind (Berrisford et al., 2011), which is significant for the mass budget and hence the energy budget. We use the data that are provided on a 256×512 Gaussian grid, with a 0.75^∘ × 0.75^∘ horizontal resolution and 60 vertical hybrid model levels. We take 6-hourly data with a range from 1979 to 2016.

2.1.2 MERRA-2

MERRA-2 (Gelaro et al., 2017) is the successor of MERRA from the Global Modeling and Assimilation Office (GMAO) of the National Aeronautics and Space Administration (NASA). It assimilates observational data with the Goddard Earth Observing System (GEOS) model and analysis scheme (Molod et al., 2015; Gelaro et al., 2017). The atmospheric state estimates are produced by a 3D-Var incremental analysis update (IAU) assimilation scheme and have coverage from 1980 to the present. Unlike most of the reanalysis products, the GEOS atmospheric model includes a finite-volume dynamical core that uses a cubed-sphere horizontal discretization (Gelaro et al., 2017). The model grid has a resolution of 0.5^∘ × 0.625^∘ with 72 hybrid levels. For this study, we use the 3-hourly assimilation data on the native model grid from 1980 to 2016.

2.1.3 JRA-55

Extending back to 1958, JRA-55 is the second reanalysis product made by the Japan Meteorological Agency (JMA) (Kobayashi et al., 2015; Harada et al., 2016). JRA-55 applies 4D-Var assimilation and it is generated on TL319 horizontal resolution with 60 hybrid levels. Before entering the satellite era in 1979, the assimilated upper air observations mainly come from radiosonde data. In this project, we take 6-hourly data from 1979 to 2015 on the original model grid, which has a horizontal resolution of 0.5625^∘ × 0.5625^∘ with 60 hybrid model levels.

2.1.4 ORAS4

Serving as the historical reconstruction of the ocean's climate, ORAS4 is the replacement of its predecessor used by the ECMWF, the reanalyses system ORAS3 (Balmaseda et al., 2013). It implements the Nucleus for European Modelling of the Ocean (NEMO) as the ocean model (Madec, 2008; Ferry et al., 2012a) and uses NEMOVAR as the data assimilation system (Mogensen et al., 2012). The model is forced by atmosphere-derived daily surface fluxes, from ERA-40 from 1957 to 1989 and ERA-Interim from 1989 to 2010. Since 2010, the forcing has changed to operational forcing (Balmaseda et al., 2013). ORAS4 produces analyses with a 3D-Var first guess at appropriate time (FGAT) assimilation scheme and spans from 1958 to the present. ORAS4 runs on the ORCA1 grid, which is associated with a horizontal resolution of 1^∘ in the extratropics and a refined meridional resolution up to 0.3^∘ in the tropics. It has 42 vertical levels, 18 of which are located in the upper 200 m. Here, we skip the first two decades and use the monthly data from 1979 to 2014 to avoid the uncertainties reported by Balmaseda et al. (2013). We use the monthly mean fields on the native model grid.

2.1.5 GLORYS2V3

GLORYS2V3 is a global ocean and sea ice eddy-permitting reanalysis system that yielded from the collaboration between the Mercator Ocean, the Drakkar consortium and Coriolis data center (Ferry et al., 2010, 2012b). It spans the altimeter and Argo eras, from 1993 to the present. The NEMO ocean model is implemented on the ORCA025 grid (approximately 0.25^∘ × 0.25^∘ with 75 vertical levels). The model is forced by a combination of ERA-Interim fluxes (e.g., shortwave radiation) and turbulent fluxes obtained with bulk formulae using ERA-Interim near-surface parameters. The data are generated by a 3D-Var assimilation scheme with temperature and salinity profiles assimilated from the CORA3.3 database (Ferry et al., 2012b). In this study, monthly data from 1993 to 2014 on the original ORCA025 grid are used.

2.1.6 SODA3

SODA3 is the latest version of Simple Ocean Data Assimilation (SODA) ocean reanalyses conducted mainly at the University of Maryland (Carton et al., 2018). SODA3 is built on the Modular Ocean Model v5 (MOM5) ocean component of the Geophysical Fluid Dynamics Laboratory CM2.5 coupled model (Delworth et al., 2012) with a grid configuration of approximately 0.25^∘ (latitude) × 0.25^∘ (longitude) × 50-level resolution (Carton et al., 2018). To be consistent with the other two reanalysis data sets assessed in this study, SODA 3.4.1 is chosen since it applies surface forcing from ERA-Interim. For this specific version, the 5 d data are available from 1980 to 2015. Reanalysis data from this period on the original MOM5 grid are used in this case.

2.2 Oceanic observations and OGCM hindcast

For independent examination of the OMET calculated from reanalysis data sets, observations of the meridional transport of mass and heat throughout the Atlantic basin are used here. We use data from the RAPID-MOCHA-WBTS program (Johns et al., 2011; McCarthy et al., 2015) and the OSNAP program (Susan Lozier et al., 2017; Lozier et al., 2019). The RAPID-MOCHA-WBTS program, which is known as the RAPID array, employs a trans-basin observing array along 26.5^∘ N and has been in operation since 2004. The OMET from the RAPID array available to this study is from April 2004 to March 2016. The OSNAP program has an observing system that comprises an integrated coast-to-coast array extending from the southeastern Labrador Shelf to the southwestern tip of Greenland and from the southeastern tip of Greenland to the Scottish shelf. So far, it provides OMET data from the full installation of the array in 2014 to the first complete data recovery in 2016 (21 months in total). Although it is too short to provide a good estimate of the interannual variability of OMET, we still include it as it is a unique observation system for OMET in the subpolar Atlantic.

Apart from the RAPID array and OSNAP observational data, a NEMO ORCA hindcast is also included here to provide more insights, since two of the chosen reanalysis products are also built on the NEMO ocean circulation model (Moat et al., 2016; Marzocchi et al., 2015). This forced model simulation implements the NEMO ORCA global ocean circulation model version 3.6 (Madec, 2008). It is configured with the ORCA0083 grid, which has a nominal resolution of 1∕12^∘ on 75 vertical levels. Climatological initial conditions for temperature and salinity were taken in January from PHC2.1 at high latitudes (Steele et al., 2001), MEDATLAS in the Mediterranean (Jourdan et al., 1998) and the rest from Levitus et al. (1998). It is forced by the surface fields produced by the Drakkar project, which supplies surface air temperature, winds, humidity, surface radiative heat fluxes and precipitation, and a formulation that parameterizes the turbulent surface heat fluxes and is provided for the period from 1958 to 2012 (data set version 5.2) (Brodeau et al., 2010; Dussin et al., 2016). More information about this hindcast is given by Moat et al. (2016). We take monthly mean data from the hindcast, which spans from 1979 to 2012. For clarity, this hindcast will be referred to as the oceanic general circulation model (OGCM) simulation in this paper.

2.3 Computation of meridional energy transport

The methods for quantification of AMET and OMET with atmospheric and oceanic reanalyses are included in this section, respectively.

2.3.1 Energy budget in the atmosphere

The total energy per unit mass of air has four major components: internal energy (I), latent heat (H), geopotential energy (ϕ) and kinetic energy (k). They are defined as

$$\begin{array}{}\text{(1)}& \begin{array}{rl}& I=c_{\mathrm{v}}T\\ & H=L_{\mathrm{v}}q\\ & \mathrm{\Phi }=gz\\ & k={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}v\cdot v,\end{array}\end{array}$$

with c_v the specific heat capacity of dry air for constant volume (J kg⁻¹ K⁻¹), T the absolute temperature (K), L_v the specific heat of condensation (J kg⁻¹), q the specific humidity (kg kg⁻¹), g the gravitational acceleration (kg m⁻¹ s⁻²), z the altitude (m) and v the zonal/meridional wind velocity (m s⁻¹). The northward propagation is positive. In addition, these four quantities can be divided into three groups: the dry static energy I+ϕ, the moist static energy $I+\mathit{\varphi }+H$ and the kinetic energy k. A constant value of L_v=2500 kJ kg⁻¹ was used to compute the AMET with the atmosphere reanalysis data sets. In addition, recently improved formulations of energy budget equations proposed by Mayer et al. (2017) and Trenberth and Fasullo (2018) are addressed here. We use an updated formulation of AMET as a combination of the divergence of dry-air enthalpy, latent heat, geopotential and kinetic energy transport, which is suggested by Mayer et al. (2017). Note that in this case the enthalpy transport associated with vapor fluxes is neglected.

In pressure coordinates, the total energy transport at a given latitude Φ_i can be expressed as (Mayer et al., 2017)

$$\begin{array}{}\text{(2)}& E=\underset{\mathrm{\Phi }={\mathrm{\Phi }}_i}{\oint }\underset{p_{\mathrm{s}}}{\overset{p_{\mathrm{t}}}{\int }}\left[(\mathrm{1}-q)c_{\mathrm{p}}T+L_{\mathrm{v}}q+gz+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}v\cdot v\right]v{\displaystyle \frac{\mathrm{d}p}{g}}\mathrm{d}x,\end{array}$$

with c_p the specific heat capacity of dry air at constant pressure, p_t the pressure level at the top of the atmosphere (Pa) and p_s the pressure at the surface (Pa). A constant value of c_p=1004.64 J kg⁻¹ K⁻¹ was used. Since we work on the native hybrid model coordinate with each atmosphere reanalysis product, the equation can be adjusted as follows (see Graversen, 2006):

$$\begin{array}{}\text{(3)}& E=\underset{\mathrm{\Phi }={\mathrm{\Phi }}_i}{\oint }{\displaystyle \frac{\mathrm{1}}{g}}\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}\left[(\mathrm{1}-q)c_{\mathrm{p}}T+L_{\mathrm{v}}q+gz+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}v\cdot v\right]v{\displaystyle \frac{\partial p}{\partial \mathit{\eta }}}\mathrm{d}\mathit{\eta }\mathrm{d}x,\end{array}$$

where η indicates the number of the hybrid level.

Unfortunately, a direct estimation of AMET based on the equations above cannot provide meaningful energy transport obtained from reanalysis data. It has been widely reported that reanalysis products suffer from mass inconsistency (Trenberth, 1991; Trenberth et al., 2002; Graversen, 2006; Graversen et al., 2007; Chiodo and Haimberger, 2010; Berrisford et al., 2011). Spurious sinks and sources mainly come from low spatial and temporal resolution, interpolation and regridding, and data assimilation. The interpolation from the original model level to pressure level can introduce considerable errors to the mass budget (Trenberth et al., 2002). Therefore, we prevent interpolations onto the pressure levels and use data on the native model levels with a high temporal resolution. Trenberth (1991) provided a method to correct the mass budget through the use of the continuity equation. The method assumes that the mass imbalance mainly comes from the divergent wind fields and corrects the overall mass budget by adjusting the barotropic wind. The conservation of mass for a unit column of air can be represented as

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{\partial p_{\mathrm{s}}}{\partial t}}+\mathrm{\nabla }\cdot \underset{p_{\mathrm{s}}}{\overset{p_{\mathrm{t}}}{\int }}v\mathrm{d}p=g(E-P),\end{array}$$

where E stands for evaporation and P denotes precipitation. It has been noted that big uncertainties reside in the evaporation and precipitation of global reanalyses (Graversen, 2006). Hence, we use the moisture budget to derive the net moisture change in the air column, according to

$$\begin{array}{}\text{(5)}& E-P={\displaystyle \frac{\partial }{\partial t}}\left(\underset{p_{\mathrm{s}}}{\overset{p_{\mathrm{t}}}{\int }}q{\displaystyle \frac{\mathrm{d}p}{g}}\right)+\mathrm{\nabla }\cdot \underset{p_{\mathrm{s}}}{\overset{p_{\mathrm{t}}}{\int }}(v\cdot q){\displaystyle \frac{\mathrm{d}p}{g}}.\end{array}$$

The related fields for the mass budget correction are surface pressure (p_s), meridional and zonal winds (u, v) and specific humidity (q). After determining the mass budget imbalance, we correct the barotropic wind fields (u_c, v_c), with u_c and v_c indicating the correction terms for zonal and meridional wind components as a result of the barotropic mass budget correction, and then calculate AMET (Trenberth, 1991). Note that all the computations regarding barotropic mass budget correction were performed in the spectral domain via spherical harmonics. Figure 1 shows the mean AMET and each component in each month at 60^∘ N estimated from ERA-Interim.

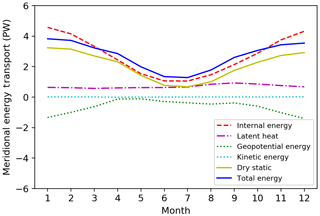
Figure 1 Estimation of mean AMET and each component in each month at 60^∘ N with ERA-Interim from 1979 to 2017.

It is worth mentioning that MERRA-2 is very different from ERA-Interim and JRA-55, in terms of the discretization method and grid incorporated by the dynamical core. The dynamical core for MERRA-2 is the GEOS-5 model and it computes all fields on a cubed-sphere grid with a resolution of 50×50 km (Gelaro et al., 2017), while in ERA-Interim and JRA-55 the computations were performed in the spectral domain. However, the data collections are saved only on the latitude–longitude grid after interpolation. Thus, the data cannot be transferred back to the cubed-sphere grid without loss of information. Moreover, the vector field computations on the cubed-sphere grid are not divergence-free due to the implementation of finite volume discretization methods (Putman and Lin, 2007). Consequently, we transferred MERRA-2 fields to the spectral domain and performed vector field computations via spherical harmonics to minimize the numerical errors, the same treatment as ERA-Interim and JRA-55.

2.3.2 Energy budget in the ocean

Unlike the atmosphere, energy transport in the ocean can be well represented by the internal energy itself. Consequently, the total energy transport in the ocean at a given latitude ϕ_i can be expressed in terms of the temperature transport (Hall and Bryden, 1982):

$$\begin{array}{}\text{(6)}& E=\underset{\mathrm{\Phi }={\mathrm{\Phi }}_i}{\oint }\underset{z_{\mathrm{b}}}{\overset{z_{\mathrm{0}}}{\int }}{\mathit{\rho }}_{\mathrm{0}}{c}_{{\mathrm{p}}_{\mathrm{0}}}\mathit{\theta }\cdot v\mathrm{d}z\mathrm{d}\mathit{\varphi },\end{array}$$

where ρ₀ is the seawater density (kg m⁻³), $c_{{\mathrm{p}}_{\mathrm{0}}}$ is the specific heat capacity of seawater (J kg^−1 ∘C⁻¹), θ is the potential temperature (^∘C), v is the meridional current velocity (m s⁻¹), and z₀ and z_b are sea surface and the depth to the bottom (m), respectively. A constant value of $c_{{\mathrm{p}}_{\mathrm{0}}}=\mathrm{3987}$ J kg^−1 ∘C⁻¹ was used in all the calculations of OMET. OHC (with unit J) is another variable that plays a role in the ocean heat budget. The total OHC between certain latitudes can be calculated by

$$\begin{array}{}\text{(7)}& \mathrm{OHC}=\underset{{\mathrm{\Phi }}_i}{\overset{{\mathrm{\Phi }}_{\mathrm{0}}}{\int }}\underset{z_{\mathrm{b}}}{\overset{z_{\mathrm{0}}}{\int }}{\mathit{\rho }}_{\mathrm{0}}{c}_{{\mathrm{p}}_{\mathrm{0}}}\mathit{\theta }\mathrm{d}z\mathrm{d}\mathit{\varphi }.\end{array}$$

Our computation of OMET suffers from a small mass imbalance (e.g., mass imbalance coming from the difference between precipitation and evaporation; Mayer et al., 2017). In the ocean, with its strong boundary circulations, even the smallest imbalance can lead to large errors in the heat flux. However, the barotropic correction method adopted by the atmosphere is not feasible here due to the mass imbalance coming from the residual between precipitation and evaporation, and some budget terms that are hard to diagnose. In oceanographic literature, it is common to use a reference temperature when calculating OMET in both observations and model diagnostics (Bryan, 1962; Hall and Bryden, 1982; Zheng and Giese, 2009). Here, we also take a reference temperature: θ_r (C). Note that the influence of taking a reference temperature on zonally integrated transport is smaller than that on a single strait (Schauer and Beszczynska-Möller, 2009). Then, the quantification of OMET becomes

$$\begin{array}{}\text{(8)}& E=\underset{\mathrm{\Phi }={\mathrm{\Phi }}_i}{\oint }\underset{z_{\mathrm{b}}}{\overset{z_{\mathrm{0}}}{\int }}{\mathit{\rho }}_{\mathrm{0}}{c}_{{\mathrm{p}}_{\mathrm{0}}}\left(\mathit{\theta }-{\mathit{\theta }}_{\mathrm{r}}\right)\cdot v\mathrm{d}z\mathrm{d}\mathit{\varphi }.\end{array}$$

Here, we take θ_r equal to 0 ^∘C. Finally, operations in the “zonal” direction are different from their conventional meaning. As the three ocean reanalysis products used here are all built on a curvilinear grid, the zonal direction on the native model grid is curvilinear as well. Similar to the considerations made in Sect. 2.1, regridding from the native curvilinear grid to a uniform geographical grid will introduce large errors. So, we worked on the original multi-pole grid and followed a zig-zag setup when taking zonal integrals. The method is illustrated by Outten et al. (2018) in their Fig. 2. After applying this method, the resulting OMET values are comparable to those in earlier publications (Trenberth and Caron, 2001; Trenberth and Fasullo, 2008; Wunsch, 2005). Note that we only have access to sub-monthly data for SODA3. The computation of OMET using monthly data in GLORYS2V3 could miss part of heat transport by eddies, while ORAS4 does not include the heat transport from the eddy parameterization scheme (Gent and Mcwilliams, 1990), as the related eddy-induced velocity field was not archived.

2.4 Statistical analysis

In order to understand the connection between MET and changes in the Arctic, and to compare to the results from numerical climate models or a single reanalysis data set (Graversen, 2006; Graversen et al., 2008; Van der Swaluw et al., 2007; Jungclaus and Koenigk, 2010; Kapsch et al., 2013), in the following section, we performed linear regressions on multiple fields with AMET and OMET. To test the significance of the regressions, we use Student's t test. The autocorrelations are taken into account. Note that all the reanalysis data sets included in this study have relatively short time series (no more than 456 months; see Table 1).

3 Results

Unless specifically noted, the results shown in this section are all based on monthly mean fields with a low-pass filter of 5 years, which will be referred to as interannual timescales for the rest of the paper.

3.1 Overview of AMET and OMET

Globally, MET is driven by the unequal distribution of net solar radiation and thermal radiation. There is transport from regions with positive net top-of-the-atmosphere (TOA) radiation to regions with negative net TOA radiation. Figure 2 shows the mean AMET and OMET over the entire time series of every product at each latitude in the Northern Hemisphere. For the atmosphere, all three data sets agree very well. The results differ a bit in amplitude but capture similar variations at each latitude. The peak of AMET is around 41^∘ N, after which it starts to decrease towards the North Pole. In ERA-Interim and JRA-55, AMET peaks at 4.45 PW at 41^∘ N, while in MERRA-2 AMET peaks at 4.5 PW at 41.5^∘ N. These findings are consistent with previous work (e.g., Trenberth and Caron, 2001; Fasullo and Trenberth, 2008; Mayer and Haimberger, 2012, and many others).

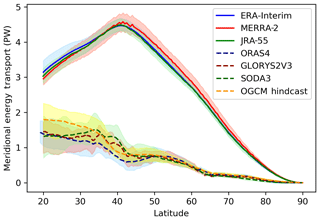
Figure 2 Mean AMET and OMET over the entire time span of each product as a function of latitude in the Northern Hemisphere. AMET is illustrated with solid lines and OMET with dashed lines. The shades represent the full range of MET across the entire time series at each latitude. The time span of each product used in this study is given in Table 1.

Apart from the climatology of MET, we are particularly interested in the variations across different timescales from midlatitudes towards the Arctic. The time series of AMET, integrated zonally over 60^∘ N, are shown in Fig. 3a. The seasonal cycle is dominant in each component, as expected, and the phase is very similar, but differences in the amplitudes are noted. The mean AMET provided by the chosen three atmospheric reanalysis data sets agrees well. However, their variations differ from each other. In ERA-Interim, the standard deviation (SD) of AMET is 0.92 PW, while MERRA-2 has a relatively large SD of 0.97 PW, and in JRA-55 the SD is 0.91 PW. Hence, it can be concluded that the seasonal cycles of AMET presented by the chosen atmospheric reanalysis data sets are similar. After removing the seasonal cycles and applying a 5-year low-pass filter, we obtain the low-frequency signals of AMET anomalies at interannual timescales (see Fig. 3b). ERA-Interim and JRA-55 agree well, and the correlation coefficient between them is 0.82. MERRA-2 provides a different result, and the correlation coefficient between ERA-Interim and MERRA-2 is −0.53. The SD of AMET anomaly in ERA-Interim is 0.02 PW, while in MERRA-2 the SD is 0.04 PW and in JRA-55 the SD is 0.03 PW. This implies that the variations of AMET anomalies at large timescales are similar in ERA-Interim and JRA-55 but not in MERRA-2. We further assess the sources of the difference in the next section.

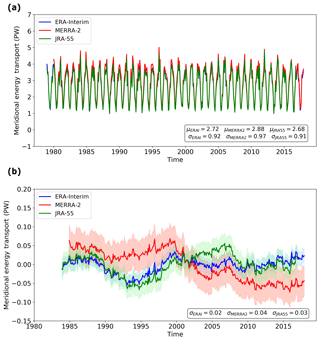
Figure 3 Time series of zonal integral of AMET at 60^∘ N without/with a low-pass filter. (a) The original time series and (b) the ones with a low-pass filter include signals from ERA-Interim (blue), MERRA-2 (red) and JRA-55 (green). For the low-pass-filtered ones, we take a running mean of 5 years. The shades represent the confidence intervals with 1 standard deviation. σ is the standard deviation and μ is the mean of the entire time series.

For the ocean, all the reanalysis data sets agree well at almost all the latitudes, except for the OMET between 30 and 40^∘ N, where the Gulf Stream resides (Fig. 2). One possible explanation is that GLORYS2V3 and SODA3 both have been generated with eddy-permitting models, while ORAS4 was not. In ORAS4, an eddy parameterization scheme from Gent and Mcwilliams (1990) is implemented. The implementation of this eddy parameterization scheme can lead to a big difference in heat transport, compared to eddy-permitting models (Stepanov and Haines, 2014). However, in this case, the computation of OMET with ORAS4 does not include the contribution from eddy-induced velocity as the fields related to the use of eddy advection schemes were not archived. The eddy-permitting reanalysis data sets with high resolution, like GLORYS2V3 and SODA3, are capable of addressing the large-scale geostrophic turbulence. It has been shown that their eddy-permitting capacity can account for the large-scale eddy variability and represent the eddy energy associated with both the Gulf Stream and the Kuroshio pathways well (Masina et al., 2017). Consequently, at the latitude of the Gulf Stream (between 30 and 40^∘ N), a strong spatial variability, which might represent more realistic patterns of the large-scale eddy variability, is apparent in all data sets but ORAS4.

Similarly, we show the zonal integral of the OMET at 60^∘ N in Fig. 4. Differences in amplitudes and trends can be observed in the unfiltered time series. The mean and SD of all the OMET time series are similar (see Fig. 4a). The mean of OMET in ORAS4 is 0.47 PW, in GLORYS2V3 it is 0.44 PW, and in SODA3 it is 0.46 PW. The OGCM hindcast gives a similar result, which is also 0.47 PW. The SD of OMET in ORAS4 and the OGCM hindcast is 0.06 PW, while in GLORYS2V3 and SODA3 the SD is 0.07 PW. The OMET anomalies with a 5-year low-pass filter are shown in Fig. 4b. OMET anomalies in ORAS4 resemble that in SODA3, especially after 1998, while OMET anomalies in GLORYS2V3 are very different from that in ORAS4 and SODA3 from 1998 to 2006. The differences reveal that the first 10 years in GLORYS2V3 are quite suspicious because of its large deviation from the other products. Such large differences should be noticeable in the heat content changes or surface fluxes. We find that OHC anomalies in GLORYS2V3 are indeed very different from ORAS4 and SODA3 during this period (see Fig. 8). Nevertheless, after 2007, all the oceanic reanalyses agree well, and the OGCM hindcast deviates from the reanalyses. It is noteworthy that the observations improve considerably around that period due to an increasing number of Argo floats in use (Riser et al., 2016). The reanalysis products used here are greatly influenced by the number of available in situ observations. We further assess the sources of differences in the next section.

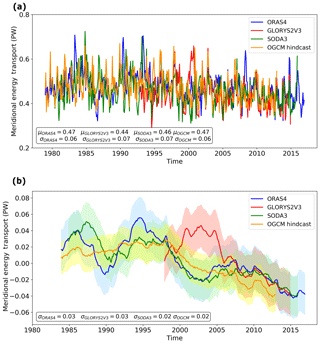
Figure 4 Time series of zonal integral of OMET at 60^∘ N without/with a low-pass filter. (a) The original time series and (b) the ones with a low-pass filter include signals from ORAS4 (blue), GLORYS2v3 (red), SODA3 (green) and the OGCM hindcast (yellow). For the low-pass-filtered ones, we take a running mean of 5 years. The shades represent the confidence intervals with 1 standard deviation. σ is the standard deviation and μ is the mean of the entire time series.

3.2 Sources of disparity

In order to further understand the difference between the AMET estimated from each atmosphere reanalysis product, we compare each component of AMET separately. We investigate the difference between each component of AMET at 60^∘ N estimated from ERA-Interim against those from MERRA-2 and JRA-55. It is noticed that the differences mainly originate from meridional temperature transport (vc_pT) and geopotential energy transport (vgz). We find that the correlation between the difference in total energy transport and the difference in meridional temperature transport between ERA-Interim and MERRA-2 is 0.55, while between ERA-Interim and JRA-55 it is 0.21. In addition, the correlation between the difference in total energy transport and the difference in geopotential energy transport (vgz) between ERA-Interim and MERRA-2 is 0.56, while between ERA-Interim and JRA-55 it is 0.60. For the other components, the correlations between them and the total difference are small. The results are all obtained with a confidence interval of 95 %. Large differences in temperature transport among reanalysis products are found at almost all latitudes (not shown). Such differences are consistent with the fact that the temperature transport and geopotential energy transport have a large contribution to the total AMET (see Fig. 1). Note that the differences in each AMET component are of the same order of magnitude as AMET. Besides, the mean and anomalous latent heat transport agree well between the chosen atmospheric products (not shown). A similar result was found by Dufour et al. (2016) in their study using more reanalysis data sets.

In order to know the relative contribution of each field to the difference of the mean total AMET among the chosen reanalyses, a direct comparison of the vertical profile of temperature and meridional velocity fields between ERA-Interim and MERRA-2 is presented in Fig. 5. We compare the monthly mean temperature and velocity fields of ERA-Interim and MERRA-2 from 1994 to 1998, in which the biggest difference was observed (Fig. 3, taking into account the running mean of 5 years). To accommodate a point-wise comparison, the fields from MERRA-2 are interpolated onto the vertical grid of ERA-Interim. It shows that these two reanalysis products differ substantially regarding each variable field (Fig. 5a and b). Big differences in temperature reside mostly at the tropopause. Large differences in meridional wind components are distributed over the entire vertical column of the tropopause. Such differences in both fields are expected to be responsible for the difference in mean temperature transport (vc_pT). Large differences are found in geopotential height fields, too (not shown). It should be noted that this comparison is carried out on pressure levels, and mass conservation is not ensured. Therefore, it can only provide insight qualitatively, and a quantitative contribution of the difference in every single field to the mean temperature transport cannot be identified here.

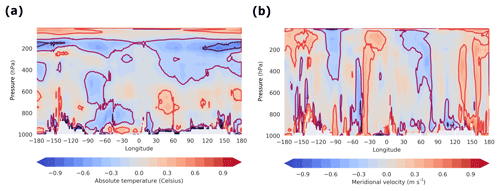
Figure 5 Difference in temperature, meridional wind velocity and temperature transport between MERRA-2 and ERA-Interim at 60^∘ N. The vertical profiles of (a) temperature difference and (b) meridional wind velocity difference are calculated from the climatology of each field from 1994 to 1998, respectively.

Differences between every two chosen atmospheric products are found at nearly each pressure level. This analysis is not sufficient to explain conclusively where the uncertainty mainly comes from in terms of the dynamics and physics in the atmosphere model and data assimilation system. We do find that uncertainties, as indicated by the spread between the data sets, in both the temperature and meridional velocity fields, are too large to constrain the AMET. Note that the difference in horizontal advection schemes can also influence the results. The chosen atmospheric reanalyses systems use semi-Lagrangian advection schemes, but this is not the case for MERRA-2. Hence, studies on low-frequency variability of energy transport and associated variables should be interpreted with care as the reanalysis products differ substantially, and we cannot judge a priori how close they are to actual energy transport since independent direct observations are not available.

For the ocean, fortunately observations of OMET in the Atlantic Ocean are available. First, OMET estimated from ORAS4, GLORYS2V3, SODA3 and the OGCM hindcast is evaluated against OMET measured at 26.5^∘ N. The intercomparison shows that the reanalysis products capture roughly the mean amplitude of the OMET (Fig. 6). Some large events are captured as well, such as the strong weakening in 2009. Statistically, the mean OMET provided by the RAPID array is 1.21±0.27 PW. It is higher than the chosen products here. The mean OMET in ORAS4 is 0.66±0.27 PW, in GLORYS2V3 it is 0.89±0.52 PW, in SODA3 it is 0.81±0.52 PW, and in OGCM hindcast it is 1.05±0.21 PW. This means that all chosen products underestimate the mean OMET at 26.5^∘ N in the Atlantic basin. Of all products, ORAS4 has the largest bias. The SD of OMET given by ORAS4 is the same as that from the RAPID array, while in GLORYS2V3 and SODA3 we find a higher SD of OMET. The OGCM hindcast has a relatively small OMET SD, which is 0.21 PW. In terms of the correlation and standard deviation, ORAS4 and the OGCM hindcast agree well with observations. It is noteworthy that the OGCM does not assimilate ocean data. The simulation is only constrained by the surface fluxes, and this suggests that the surface forcing is a very important driver of OMET variability. To conclude, the heat transport at 26.5^∘ N is too low in these products, but ORAS4 and OGCM hindcasts appear to have reasonable variability.

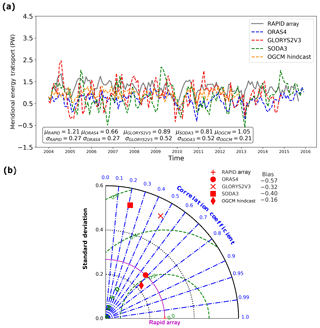
Figure 6 OMET estimated from ORAS4 (blue), GLORYS2V3 (red), SODA3 (green) and the OGCM hindcast (orange) compared to the RAPID array observation (gray) at 26.5^∘ N across the Atlantic basin. The time series of OMET is presented in panel (a). The statistical properties are shown in (b) the Taylor diagram, including bias, correlation (blue), standard deviation (black) and root mean square deviation (green). σ is the standard deviation and μ is the mean of the entire time series.

Moreover, the comparison of time series in the chosen reanalyses and OSNAP observations is given in Fig. 7. Due to the limited length of OMET time series, only ORAS4 and SODA3 are included in the comparison. It can be noticed that the OMET given by ORAS4 is comparable to that in OSNAP in terms of the amplitude and variability. For most of the time within the observation period, OMET in ORAS4 falls into the range of the OSNAP observation including the uncertainty margins. The mean of OMET in ORAS4 is 0.39±0.11 PW, which is quite similar to the mean OMET (0.45±0.07 PW) of OSNAP. However, OMET in SODA3 has a larger mean and standard deviation than that in OSNAP and thus deviates from the observations.

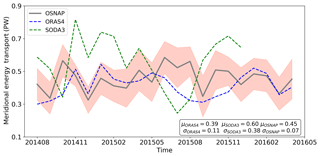
Figure 7 OMET estimated from ORAS4 (blue), SODA3 (green) and compared to the OSNAP observation (gray) at subpolar Atlantic basin. The range of uncertainty from OSNAP observation is marked by the red shade. σ is the standard deviation and μ is the mean of the entire time series.

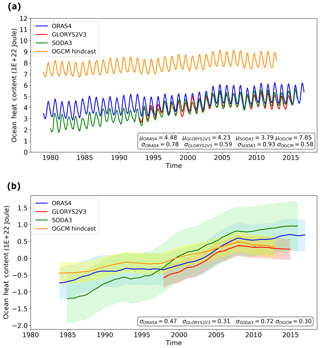
Figure 8 Time series of (a) OHC and (b) OHC anomalies with a low-pass filter at the polar cap. The OHC is integrated from surface to the bottom between 60 and 90^∘ N. It is estimated from ORAS4 (blue), GLORYS2V3 (red), SODA3 (green) and the OGCM hindcast (yellow). The shades represent the confidence intervals with 1 standard deviation. σ is the standard deviation and μ is the mean of the entire time series.

Just as in the atmosphere, we would like to study the temperature and meridional current velocity contributions to the ocean heat transport to identify the sources of the difference between products. However, due to the nature of the curvilinear grid, the comparison of local fields after interpolation is not trustworthy. To get further insight, we calculate the OHC, since the convergence of the heat transport is likely related to OHC change. A full budget analysis was not feasible as most data sets did not include the surface fluxes. Figure 8 illustrates the OHC (Fig. 8a) and OHC anomalies (Fig. 8b) quantified from ORAS4, GLORYS2V3, SODA3 and the OGCM hindcast. It depicts the OHC integrated in the polar cap (from 60 to 90^∘ N) over all depths. The mean OHC in ORAS4 is $\mathrm{4.48}\pm \mathrm{0.78}\times {\mathrm{10}}^{\mathrm{22}}$ J, in GLORYS2V3 it is $\mathrm{4.23}\pm \mathrm{0.59}\times {\mathrm{10}}^{\mathrm{22}}$ J, and in SODA3 it is $\mathrm{3.79}\pm \mathrm{0.93}\times {\mathrm{10}}^{\mathrm{22}}$ J, while the OGCM hindcast shows a much larger mean OHC of $\mathrm{7.85}\pm \mathrm{0.58}\times {\mathrm{10}}^{\mathrm{22}}$ J. Actually, we found that the OHC between 60 and 70^∘ N in the OGCM hindcast agrees well with the reanalyses (not shown). Thus, the difference seems to be associated with changes to the sea ice distribution. Given the limited observations in the Arctic to constrain the reanalyses and different assumptions about the Arctic sea ice due to the differences in spatial resolutions, it is more complex than just concluding that the reanalyses are better. The variations of OHC are similar between chosen products. Regarding the OHC anomalies in Fig. 8b, a positive trend of OHC anomalies in the polar cap is captured by each product. However, the variability is different, and these are reflected in the standard deviation of OHC anomalies time series. Increases in surface temperature and OHC are often taken as a sign of AA in many papers (e.g., Serreze and Barry, 2011). Qualitatively, the trends of OHC in the chosen reanalyses at the polar cap could be taken as a sign of the AA, but it might be just Arctic warming and not necessarily a higher warming rate than the global mean temperature change. A quantitative evaluation of the AA is not possible due to large differences between products. To conclude, there are large differences in OHC between chosen products, while their variations agree relatively well. Since OHC is a function of temperature fields only, this can imply that temperature profiles are different among the chosen ocean reanalysis data sets. The differences of OHC between chosen products are partially consistent with the differences that we found for OMET. However, the OHC anomalies agree better among reanalysis products than the absolute OHC, which indicates that the trend of OHC is captured in a similar way among all the ocean reanalysis products.

3.3 MET and the Arctic

In previous sections, it is found that MET values in different reanalysis products at subpolar and subtropical latitudes differ substantially from each other. In order to further evaluate AMET and OMET given by different reanalyses and to provide more insight, we investigate the links between MET and remote regions. We focus on the Arctic because previous studies indicate a strong role for subpolar MET in low-frequency variability in the Arctic region. Given the complexity of the interaction between MET and the Arctic, and the short time series available, determining cause–effect relations is out of the scope of this paper. We aim to compare the relation between MET and the Arctic within each reanalysis product to investigate the physical plausibility and compare it with previous studies that use data from one reanalysis product or from coupled climate models (e.g., Graversen, 2006; Graversen et al., 2008; Van der Swaluw et al., 2007; Jungclaus and Koenigk, 2010; Kapsch et al., 2013).

Many of these studies perform linear regressions between a time series of MET and grid-point values of other physical variables. Here, we follow the same procedure and perform linear regressions of sea level pressure (SLP), 2 m temperature (T2M) and sea ice concentration (SIC) anomalies on AMET and OMET anomalies at 60^∘ N for the chosen products. We show linear regressions in summer and winter separately in order to account for the seasonal variability of the relationships. It should also be noted that there are strong trends in OMET, T2M and SIC. We removed them by applying a polynomial fit to the time series on each grid point. We find that the second-order polynomial fit is able to capture the trend without losing variations at interannual timescales. Hereafter, we only address detrended OMET, T2M and SIC. For the sake of consistency, the regressions are carried out on the surface fields included in each respective reanalysis product. For instance, the regression of SLP on AMET estimated from ERA-Interim involves SLP fields from ERA-Interim itself. For the ocean reanalyses, as they all apply forcing derived from ERA-Interim, the regressions are performed on the fields from ERA-Interim. Note that there is a known issue with the quality of the sea ice field close to the North Pole in ERA-Interim, which can be inferred from an evaluation of reanalysis data sets concerning near-surface fields in Lindsay et al. (2014). Following the regressions performed by Van der Swaluw et al. (2007) and Jungclaus and Koenigk (2010), we repeated the same procedure here with AMET at interannual scales (∼5 years).

First, we investigate the links between MET and the Arctic in winter. The regressions of anomalies of multiple fields on AMET anomalies at 60^∘ N in each atmospheric product in winter are shown in Fig. 9. The regression coefficients reach their maximum when the regressions are instantaneous with given fields. In ERA-Interim and JRA-55, AMET is correlated with SLP over the Greenland, the North Atlantic, the Barents Sea, the Kara Sea and the northern part of the Eurasian continent. It suggests that an increase in subpolar AMET is linked to a northward advection over the Greenland which could bring relatively warm and humid air into the Arctic. Such patterns are consistent with the relatively warm air over the Greenland and part of the central Arctic close to the Eurasian side shown in Fig. 9d and f. Using ERA-40, Graversen (2006) found a similar correlation between AMET and surface air temperature (SAT) in the Greenland Sea and Barents Sea as Fig. 9d and f, without time lag. This is also consistent with a model study by Jungclaus and Koenigk (2010). The decrease of sea ice concentration with increasing AMET in Baffin Bay and the northern part of the Barents Sea given in Fig. 9g and i is consistent with the relations between AMET and T2M. A further eddy decomposition of AMET following the method from Peixoto and Oort (1992) indicates that heat transported by standing eddies has the biggest contribution to the total AMET (not shown), which is consistent with Graversen and Burtu (2016). These patterns are found only in ERA-Interim and JRA-55 but not in MERRA-2. Such different patterns in MERRA-2 likely stem from its shift in AMET around 2000. Hence, there is also large uncertainty in the assertion that heat and humidity transport by stationary eddies contributes to the changes in the subpolar and Arctic regions at interannual timescales.

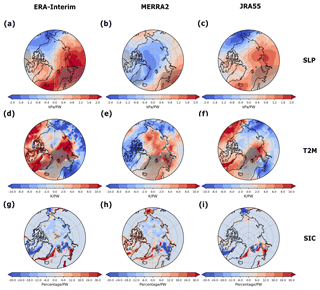
Figure 9 Regressions of sea level pressure, 2 m temperature and sea ice concentration anomalies on AMET anomalies at 60^∘ N in winter (DJF) at interannual timescales with no time lag. The monthly mean fields are used here after taking a running mean of 5 years. Both the 2 m temperature and sea ice concentration are detrended. From left to right, they are the regressions on AMET of (a, d, g) ERA-Interim, (b, e, h) MERRA-2 and (c, f, i) JRA-55. The stippling indicates a significance level of 95 %.

Moreover, similar to Van der Swaluw et al. (2007) and Jungclaus and Koenigk (2010), we investigate the links between the variability of OMET and variations of multiple fields at interannual timescales. The regressions of anomalies of multiple fields on detrended OMET anomalies at 60^∘ N in winter are shown in Fig. 10, with OMET leading by 1 month. It is noteworthy that it takes around 1 to 2 years for the OMET anomalies to propagate from the North Atlantic to the Barents Sea (Årthun et al., 2012). However, the regression coefficients are maximal when the OMET leads by 1 month, which could be attributed to the implementation of the low-pass filter. In ORAS4 and SODA3, increasing OMET can lead to a decrease in SLP in the Arctic, while in ORAS4 this polar low is much stronger. This seems to indicate that an increase in OMET is related to sea ice melt and increase in T2M around the Nordic Seas. There is an Arctic Oscillation (AO)-/North Atlantic Oscillation (NAO)-like SLP anomaly with the associated large-scale temperature pattern. However, GLORYS2V3 tells an entirely different story. This is mainly due to the difference between OMET in this data set compared to the other ocean data sets during the 1990s, as shown in Fig. 4.

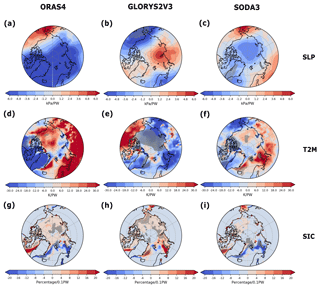
Figure 10 Regressions of sea level pressure, 2 m temperature and sea ice concentration anomalies on OMET anomalies at 60^∘ N in winter (DJF) at interannual timescales. OMET leads the fields by 1 month. The 2 m temperature, sea ice concentration and OMET are detrended. From left to right, they are the regressions on OMET of (a, d, g) ORAS4, (b, e, h) GLORYS2V3 and (c, f, i) SODA3. The stippling indicates a significance level of 95 %.

In general, the decrease of OMET leads to an increase in the growth rate of SIC, which is consistent with studies performed with global climate models at decadal to interdecadal timescales (e.g., Van der Swaluw et al., 2007; Jungclaus and Koenigk, 2010; van der Linden et al., 2016). Studies with observations of sea ice in the Barents Sea and OMET across the Barents Sea Opening (BSO) also confirm the strong correlation between the OMET and sea ice variation over the Barents Sea (Årthun et al., 2012; Onarheim et al., 2015). However, note that some discussed regions are below the significance of 95 %.

In summer, the situation becomes more intricate and unclear. The same regressions of anomalies of multiple fields on AMET and OMET anomalies at 60^∘ N in each reanalysis product in summer are included in the Supplement. It is noted that the consistency of associations between AMET, OMET and multiple fields is better in winter than that in summer within the chosen products. Atmospheric dynamical processes are more dominant in winter, which is also reflected in large-scale patterns of variability such as the AO and NAO which are more pronounced in winter than in summer (e.g., Lian and Cess, 1977; Curry et al., 1995; Goosse et al., 2018). Therefore, the regressions of SLP, T2M and SIC on AMET in winter are easier to understand than those in summer.

In this section, we compared the reanalysis data with findings from previous studies. We found that ERA-Interim and JRA-55 are most consistent with the results given by coupled numerical models in winter, while MERRA-2 does not corroborate model studies. For the ocean, results from ORAS4 and SODA3 are more consistent with literature in winter. However, given the low statistical significance and the difference among chosen products, it is still hard to determine which atmospheric product provides more convincing plausible interannual variations in AMET.

4 Discussion

In this study, we found substantial differences between reanalysis products with respect to MET. In order to improve the accuracy of the variability of AMET and OMET estimated from reanalyses, one needs more observations to constrain the models. Vertical profiles differ substantially between products, and surface and top-of-the-atmosphere radiation budget are too uncertain to constrain variability in the different products. Note that reanalyses do not assimilate direct observation of the TOA and surface energy budgets. Climate models already provide information on the interaction between atmosphere and ocean and connections provided by the energy transport from midlatitudes to high latitudes (Shaffrey and Sutton, 2006; Van der Swaluw et al., 2007; Jungclaus and Koenigk, 2010). This can potentially sketch the mechanism of the interaction between energy transport and the Arctic climate change. Moreover, some studies point out that the latent heat is more influential on the Arctic sea ice rather than the dry static energy (Kapsch et al., 2013; Graversen and Burtu, 2016). With improved reanalysis products and independent observations, such as ocean mooring arrays and atmospheric in situ and satellite observations, to validate the reanalyses, the validity of these mechanisms can be further studied.

The regression of SIC on OMET suggests that sea ice variations are sensitive to changes of meridional energy transport at subpolar latitudes, which is noticed by other studies on SIC and MET as well (Van der Swaluw et al., 2007; Jungclaus and Koenigk, 2010; van der Linden et al., 2016). ORAS4 and SODA3 show a large anticorrelation between SIC and OMET in winter around the Greenland Sea and the Barents Sea. However, GLORYS2V3 does not show this relation. The differences in OMET are reflected in the regressions on sea ice. The strong connection between OMET from mid-to-high latitudes and the Arctic sea ice indicates an indirect link between midlatitudes and the Arctic. Many studies that explored these remote links found large-scale “horseshoe” and dipole patterns over the Atlantic (Czaja and Frankignoul, 2002; Gastineau and Frankignoul, 2015; Delworth et al., 2017). However, the physical mechanism remains disputable. Overland et al. (2015); Overland (2016) propose that the multiple linkages between the Arctic and midlatitudes are based on the amplification of existing jet stream wave patterns, which might also be driven by tropical and midlatitude sea surface temperature (SST) anomalies (Screen and Francis, 2016; Svendsen et al., 2018). Cohen et al. (2014) lists possible pathways for the teleconnection between the Arctic and midlatitudes, including changes in storm tracks, the jet stream, and planetary waves and their associated energy propagation. However, due to the shortness of time series, a small signal-to-noise ratio, uncertain external forcing and the internal atmospheric variability (Overland, 2016; Barnes and Screen, 2015), this question has no easy answer.

Previous studies have shown that the variations of total OMET are very sensitive to the changes of its overturning component (e.g., McCarthy et al., 2015; Lozier et al., 2019). Hence, the Atlantic meridional overturning circulation (AMOC) may serve as an indicator of the changes of OMET. In our case, a quantitative estimation of the difference in the AMOC among the chosen data sets is beyond the scope of this paper. However, the downward trend of AMOC, which has been reported by several studies (Smeed et al., 2014; McCarthy et al., 2015; Oltmanns et al., 2018), is consistent the downward trend observed in OMET at 60^∘ N in our chosen oceanic reanalyses (see Fig. 4). After analyzing six oceanic reanalysis data sets, Karspeck et al. (2017) find the reanalysis products are not consistent in their year-to-year AMOC variations. The discrepancy between AMOC represented by each reanalysis product may explain the differences in OMET in each reanalysis data set.

5 Conclusions

This study aimed to quantify and intercompare AMET and OMET variability from three atmospheric and three oceanic reanalysis data sets at subpolar latitudes. It also serves to illustrate the relation between AMET and OMET with high-latitude climate characteristics. The study is motivated by previous studies with coupled models that show a strong relation between meridional energy transport and sea ice. It is also motivated by previous studies with reanalysis data, where generally only one reanalysis data set is considered and which include mostly only oceanic or atmospheric analysis.

All selected data sets agree on the mean AMET and OMET in the Northern Hemisphere. The results are consistent with those achieved over the previous 20 years (Trenberth and Caron, 2001; Fasullo and Trenberth, 2008; Mayer and Haimberger, 2012). However, when it comes to anomalies at interannual timescales, they differ from each other both spatially and temporally. The variations between ERA-Interim and JRA-55 are small, while MERRA-2 is very different from them. Although there is an overlap of observational data assimilated by different reanalysis products, large deviations still exist in many fields, especially for the vertical profiles of temperature and velocity in atmospheric reanalyses, which were also reported by some reanalysis quality reports (Simmons et al., 2014, 2017; Uotila et al., 2018). A further investigation of the relations between multiple fields in the Arctic and meridional energy transport shows that the Arctic climate is sensitive to the variations of AMET and OMET in winter. The patterns in ERA-Interim and JRA-55 are more consistent in winter. For the ocean, ORAS4 and SODA3 provide similar patterns in winter. Based on our results, it seems that the interannual variability of AMET and OMET cannot be constrained by the available observations. The existence of sources and sinks in reanalysis data sets introduces large uncertainties in the computation of energy transport (Trenberth, 1991; Trenberth and Solomon, 1994). Although the reanalysis data sets are not specifically designed for the studies on energy transport, given the good agreement on mean AMET and OMET and their annual cycles among assessed reanalysis products, we still recommend to use these reanalysis products for the energy transport diagnostics. However, much care should be taken when adopting reanalyses for the examination of energy transport at relatively long timescales. The robustness of those results based on the AMET and OMET estimated from reanalyses should be further assessed.