Variability of surface climate in simulations of past and future

It is virtually certain that the mean surface temperature of the Earth will continue to increase under realistic emission scenarios, yet comparatively little is known about future changes in climate variability. This study explores changes in climate variability over the large range of climates simulated by the Coupled Model Intercomparison Project Phase 5 and 6 (CMIP5/6) and the Paleoclimate Modeling Intercomparison Project Phase 3 (PMIP3), including time slices of the Last Glacial Maximum, the mid-Holocene, and idealized experiments (1 % CO₂ and abrupt4×CO₂). These states encompass climates within a range of 12 ^∘C in global mean temperature change. We examine climate variability from the perspectives of local interannual change, coherent climate modes, and through compositing extremes.

The change in the interannual variability of precipitation is strongly dependent upon the local change in the total amount of precipitation. At the global scale, temperature variability is inversely related to mean temperature change on intra-seasonal to multidecadal timescales. This decrease is stronger over the oceans, while there is increased temperature variability over subtropical land areas (40^∘ S–40^∘ N) in warmer simulations. We systematically investigate changes in the standard deviation of modes of climate variability, including the North Atlantic Oscillation, the El Niño–Southern Oscillation, and the Southern Annular Mode, with global mean temperature change. While several climate modes do show consistent relationships (most notably the Atlantic Zonal Mode), no generalizable pattern emerges. By compositing extreme precipitation years across the ensemble, we demonstrate that the same large-scale modes influencing rainfall variability in Mediterranean climates persist throughout paleoclimate and future simulations. The robust nature of the response of climate variability, between cold and warm climates as well as across multiple timescales, suggests that observations and proxy reconstructions could provide a meaningful constraint on climate variability in future projections.

1 Introduction

Knowledge of slow and sustained changes in mean climate conditions is important for understanding climatic risks and uncertainties (IPCC-AR5, 2013). However, understanding changes in the variability around the mean is at least as pressing of an issue as understanding changes in mean climate for society and agriculture (Katz and Brown, 1992). This is because societal (Alexander and Perkins, 2013; Katz and Brown, 1992; Hsiang et al., 2013) and ecosystem (Seddon et al., 2016; Stenseth, 2002) impacts scale with climate variability, and increasing variability leads to increasing extreme events (IPCC-AR5, 2013; Schär et al., 2004).

Climate variability can be defined as variations in the mean state and other statistics (e.g., standard deviations, frequency of occurrence of extremes) of temperature, precipitation, and atmospheric circulation on spatial and temporal scales beyond individual weather events (Qin et al., 2014; Xie et al., 2015). Internal variability arises due to complex (often nonlinear) internal processes within the atmosphere–ocean–biosphere–cryosphere system (Deser et al., 2012a; Olonscheck and Notz, 2017; Lofverstrom, 2020) or as forced variability in response to changes in natural or anthropogenic forcing (Foster and Rahmstorf, 2011). However, the actual evolution of climate combines anthropogenic forcing and natural climate variability (Horton et al., 2016), with internal variability dominating the local to regional synoptic evolution (e.g., Deser et al., 2012a; Wallace et al., 2015). In a simple stochastic model (Hasselmann, 1976), internal variability is proportional to climate sensitivity and has been used to derive emergent constraints from temperature variability over the historical era (Cox et al., 2018). A core focus of research has been the investigation of major modes of climate variability (Qin et al., 2014), such as the El Niño–Southern Oscillation (Walker and Bliss, 1932; Bjerknes, 1966), and their contemporary change and representation by climate models (Deser et al., 2010, 2012a; Phillips et al., 2014). Their projected changes and relevance for future regional climate evolution remain uncertain (Xie et al., 2015; Christensen et al., 2013). At the same time, atmospheric circulation changes contribute strongly to internal climate variability and, inherently, uncertainty in future projections (Thompson et al., 2015).

Trends established based on the instrumental record are uncertain, and both increasing (Hansen et al., 2012) and decreasing (Rhines and Huybers, 2013; Lenton et al., 2017) trends in temperature variability have been reported. These trends differ amongst world regions (Rhines and Huybers, 2013; Huntingford et al., 2013): more economically underdeveloped areas are generally more vulnerable to increases in temperature variability than the more high-latitude developed regions (Bathiany et al., 2018). In any region, climate impacts are expected to increase with greater variability (Katz and Brown, 1992; Alexander and Perkins, 2013). Therefore, there is a need to better understand changes to climate variability under warming. A warming similar to that projected for the next centuries (IPCC-AR5, 2013) occurred around the Last Glacial Maximum (LGM; 27–19 thousand years before present, 27–19 kyr BP) until apparently stable Holocene climate conditions were reached (since 11.7 kyr BP). Along with this warming, a reduction in centennial- to millennial-scale temperature variability to a quarter of the glacial level was estimated based on paleoclimate proxy data and linked to the reduction of the local meridional temperature gradients (Rehfeld et al., 2018). Based on this mechanistic link, a continued decrease in temperature variability at the global scale could be expected at long timescales (Rehfeld et al., 2018). It is, however, unclear how these long timescales affect the synoptic to decadal variability, which is not generally observable with paleoclimate proxies. There is corroborating evidence based on model simulations for decreases in variability at interannual (Holmes et al., 2016) and longer (Brown et al., 2017) timescales. In particular, the observed reduction in Arctic sea ice extent has been linked a decline in temperature variability at a global scale (Huntingford et al., 2013; Olonscheck and Notz, 2017; Bathiany et al., 2018). At the seasonal scale, higher temperature variability over Northern Hemisphere (NH) land in summer has been observed (Holmes et al., 2016), consistent with increases in summer extremes (Coumou and Rahmstorf, 2012; Pfleiderer et al., 2019).

Changes in warm temperature extremes are linked to the local mean temperature change (Rhines and Huybers, 2013), but increasing synoptic variability could contribute to more frequent heat waves (Horton et al., 2016), circulation changes to larger winter temperature variability (Screen and Simmonds, 2014), and the persistence of weather patterns (Francis and Vavrus, 2012). For example, observed increases in both mean precipitation and precipitation variability have been linked to warming (Pendergrass et al., 2017; Collins et al., 2013; Allen and Ingram, 2002; Held and Soden, 2006). In most climate models, precipitation variability was found to increase over land for future warming scenarios, with variability increasing at a similar or higher rate than the mean (Pendergrass et al., 2017). At synoptic to interannual timescales, local temperature variability and precipitation variability are negatively correlated over continental areas (Trenberth and Shea, 2005; Rehfeld and Laepple, 2016). Conversely, at longer timescales and at the global scale, a positive relationship has been found (Rehfeld and Laepple, 2016; Adler et al., 2008; Allen and Ingram, 2002). Precipitation changes are, however, strongly linked to changes in circulation and internal variability that remain poorly understood (Hawkins, 2011; Christensen et al., 2013; Deser et al., 2012a).

Here we investigate the link between mean state and variability changes in temperature and precipitation across a wide range of global mean temperatures. In particular, we examine changes in climate variability on interannual to multidecadal timescales in simulations conducted in the framework of the Paleoclimate Modeling Intercomparison Project Phase 3 (Braconnot et al., 2012, PMIP3), as well as the Coupled Model Intercomparison Project Phase 5 (CMIP5; Taylor et al., 2012) and Phase 6 (CMIP6; Eyring et al., 2016a) with which it is affiliated. We contrast changes in interannual variability across simulations for the LGM (denoted lgm in the following), the mid-Holocene (midHolocene; 6000 years before present), and idealized warming scenarios with a 1% CO₂ increase per year (1pctCO2), as well as an abrupt quadrupling of CO₂ (abrupt4xCO2). Section 2 gives details on these experiments as well as the data preprocessing and comparison metrics. Section 3 examines changes in local interannual variability, modes of variability, the drivers of extreme precipitation changes, and the spectrum of variability. In Sect. 4 we discuss how this compares to previous findings and identify key uncertainties. We conclude in Sect. 5 with a discussion on prospects for the validation of modeled climate variability.

2 Data and methods

2.1 Model simulations

The core aim of this study is to compare past and future climate simulations and to assess the similarities – or differences – in climate variability across different Earth system states. We consider a range of state-of-the-art climate models (listed in Table 1) based on climate model experiments coordinated by the Coupled Model Intercomparison Project (CMIP) Phase 5 (CMIP5; Taylor et al., 2012) and Phase 6 (CMIP6; Eyring et al., 2016a) as well as the corresponding Paleoclimate Model Intercomparison Project Phase 3 (PMIP3; Braconnot et al., 2012). There are 25 climate models considered in this study (Table 1 and Fig. 1). We use a single ensemble member for each model (generally r1i1[p1]f1) and climate state. The preindustrial control (piControl) simulations represent constant preindustrial (PI) conditions and are the baseline for comparison in all our analyses. We analyze the air surface temperature (“tas”), precipitation (“pr”), sea surface temperature (SST), and sea level pressure (SLP) variables.

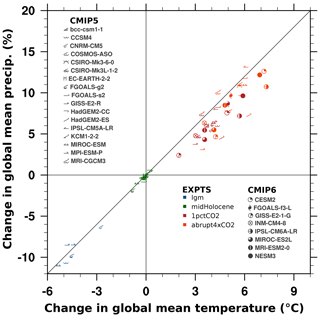
Figure 1 Hydrological sensitivity across the past and future model ensemble. The change in global mean temperature from the PI is plotted against the percentage of change in the global mean precipitation rate. Symbols indicate the different climate models, following Table 1. Colors show the different experiments. The line indicates a 2 % change in precipitation per Kelvin temperature change.

2.2 The last glacial maximum experiment (lgm)

The last glacial maximum experiment (lgm) represents conditions 21 000 years ago. Globally averaged surface temperature was about 3–5^∘ colder than today (Annan and Hargreaves, 2013; Shakun and Carlson, 2010) in response to a global mean radiative forcing of about −4 W m⁻² (Broccoli, 2000) by reduced greenhouse gas (GHG) concentrations, large continental ice sheets, and a 120–130 m lower sea level (Clark and Mix, 2002; Broccoli, 2000; Annan and Hargreaves, 2015). A standard set of forcings (orbit, GHG) and surface boundary conditions (ice sheets) was set out in PMIP3 (Braconnot et al., 2012; PMIP3, 2010). In particular, the ice sheet extent and height are modified with respect to the piControl configurations to reflect the extensive LGM NH ice sheet cover. The CO₂ concentration is prescribed at 185 ppm, CH₄ at 350 ppb, and N₂O at 200 ppb (PMIP3, 2010), whereas the solar constant, vegetation, and aerosols follow the preindustrial control setup (Taylor et al., 2012). Overall, insolation was higher than preindustrial in winter in both hemispheres and lower than preindustrial in summer in both hemispheres (up to −12 W m⁻² in NH high latitudes; Otto-Bliesner et al., 2006). This corresponds to a reduced seasonal contrast in the top-of-atmosphere radiation. The multimodel mean shows global cooling that is strongest in the polar regions and above ice sheets (Fig. 2a).

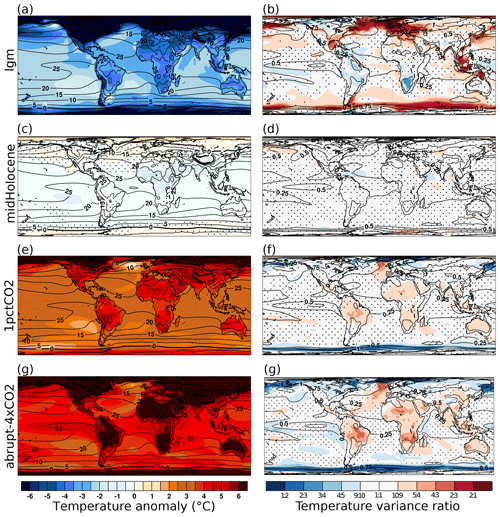
Figure 2 The change in mean annual temperature (a–d) and its variability (e, f) across multiple climate experiments. Each panel shows the ensemble average difference. The changes in the mean temperature are calculated as the experiment minus preindustrial control grid box annual means. The changes in variability are given based on the ratio of the standard deviation of annual mean temperature in the experiment to that of the piControl experiment. Ratios above 1 indicate higher variability in the experiment than in the piControl. The contours in each panel show the ensemble mean pattern in the preindustrial control. Contour variations are due to the different number of models available for individual experiments, as the preindustrial ensemble mean is only computed from models in each experiment. Stippling indicates where the sign of the change disagrees for more than two-thirds of the ensemble.

Table 1 Details of the models and experiments involved in the analysis. Each experiment provides the global mean change in surface temperature from the preindustrial control simulation (ΔT). The (actual) hydrological sensitivity (HS) is the global mean percentage of change in precipitation divided by the temperature change. It is was calculated via linear regression through all the simulations if available. Where fewer experiments existed, it was calculated as the directed average of the values, excluding the midHolocene simulation.

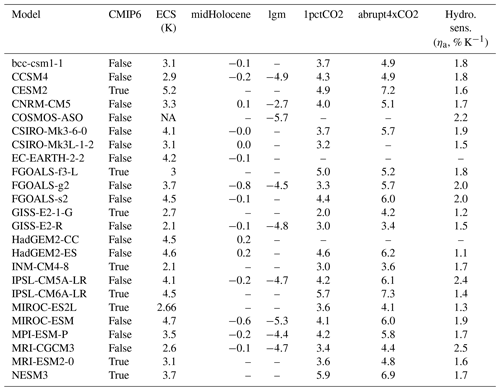
NA stands for not available.

2.3 The mid-Holocene experiment (midHolocene)

The midHolocene experiments represent conditions at 6000 years before present, during the peak warmth of the current interglacial (Taylor et al., 2012; Braconnot et al., 2012). The different orbital configuration (with higher-than-present-day obliquity and eccentricity) led to an enhanced seasonal contrast in insolation, with stronger insolation in June to September from the high northern latitudes down to 30^∘ S (up to 32 W m⁻² in NH summer), stronger insolation in September to November in SH spring (+48 W m⁻²) (30 to 90^∘ S), and negative insolation anomalies of similar magnitude in the other months of the year (Otto-Bliesner et al., 2006). This led to a weak global mean insolation anomaly. Greenhouse gas concentrations in the PMIP3 ensemble were prescribed as for the piControl simulation (∼280 ppm CO₂, 650 ppb CH₄, 270 ppb N₂O), as were the configurations of vegetation, aerosols, ice sheets, topography, and coastlines (PMIP3, 2010). In previous model intercomparison exercises, global mean temperatures were found to be similar to today (Otto-Bliesner et al., 2006), but proxy data from the NH support warmer temperatures (Wanner et al., 2015; Marcott et al., 2013).

2.4 The warming experiments 1pctCO2 and abrupt4xCO2

To complement the paleoclimate simulations, we analyze two experiments that each model from CMIP5 and CMIP6 performed: the idealized warming experiments 1pctCO2 and abrupt4xCO2 (Taylor et al., 2012; Eyring et al., 2016a). In the abrupt4xCO2 experiment, the atmospheric CO₂ concentration is abruptly quadrupled from preindustrial conditions to analyze fast feedbacks and climate sensitivity (Eyring et al., 2016a). The simulations are continued for at least 150 years. We analyze the years 100–150 for all simulations. Note that we follow the naming scheme of CMIP5 (abrupt4xCO2; Taylor et al., 2012), while in CMIP6 the experiment name is abrupt-4xCO2 (Eyring et al., 2016a). The experimental protocols are equivalent between the CMIP generations (Taylor et al., 2012). The CO₂ concentrations in the 1pctCO2 simulations are prescribed to increase by 1 % per year in a compound fashion starting from preindustrial conditions (Eyring et al., 2016a). The change in global mean temperature at the time of CO₂ doubling in this experiment is called the transient climate response (TCR; Andrews et al., 2012). This compound increase achieves a quadrupling of carbon dioxide after 140 years, but the climate system is still highly transient. The 1pctCO2 simulations are run between 140 and 160 years, of which we analyze the final 50 years. The realized warming in the 1pctCO2 scenarios is less than in the abrupt4xCO2 runs (Table 1), as the system is still further from equilibration.

2.5 Preprocessing of model simulations

The model output is treated in a consistent fashion across all the analyses. We always analyze the final 50 years of each simulation, except for in the abrupt4xCO2 experiment, wherein the years 100 to 149 are analyzed. For the variability analyses, output is converted to anomalies with respect to the monthly climatology over the 50 years. These anomalies are then linearly detrended at each grid point.

This process removes the changing mean state in the transient simulations and is based on the conventions of the Climate Variability Diagnostics Package (CVDP; Phillips et al., 2014; Eyring et al., 2016b). The analyses performed here primarily focus on interannual timescales, and therefore we do not apply the PaleoCalAdjust software to account for the output-averaging calendar effects (Bartlein and Shafer, 2019).

2.6 Comparisons across the ensemble

All model output used in the study is available for download on the Earth System Grid Federation (Eyring et al., 2016b). Each model is weighted equally during ensemble averaging. These experiments provide a large range of global mean temperature (GMT) changes (Fig. 1) ranging from −6 to +6.5 K with respect to the preindustrial state. Over this range of 12 K in GMT, the area-weighted global mean precipitation (GMP) varies between −12 % for the lgm experiments and +12 % for the abrupt4xCO2 experiments. The slope of the relationship between temperature change and precipitation change is known as the hydrological sensitivity (HS; O'Gorman et al., 2011). For CMIP5 and CMIP3 models, values between 2 and 3 % K⁻¹ have been established (Li et al., 2013; O'Gorman et al., 2011; Allen and Ingram, 2002). Based on the mean temperature and precipitation values for each model (Fig. 1), we calculate HS individually for each general climate model (GCM) (Table 1) and explore ensemble-wide relationships (Sect. 3.1 and 3.2).

2.7 Diagnosing variability changes

This research spans several different definitions of variability described in the literature. We term the kind of variability analyzed by, e.g., Huntingford et al. (2013) and Pendergrass et al. (2017) as “local variability” in that it considers the year-to-year variations at an individual location. There has been a concerted effort to investigated the preferred spatial patterns and temporal variations that account for large-scale features of variance in the climate system. We term these as “modes of climate variability”, and they are considered to be the product of a specific spatial pattern and an associated index time series (Qin et al., 2014). They are diagnostic measures for teleconnections or surface climate patterns defined on pressure, temperature, or precipitation fields. Here, we investigate the changes in 10 modes of variability from the detrended time series following the workflow of the Climate Variability Diagnostics Package (CVDP; Phillips et al., 2014). We investigate seven atmospheric–oceanic coupled modes defined as predominant SST patterns and three extratropical atmospheric modes with large-scale teleconnection patterns (Deser et al., 2010; Nigam, 2003). Internal variability of the jth mode, σ_int,j, was estimated across the N different models from $\mathrm{1}/N\sum _{i=\mathrm{1}}^N{x}_{i,j,\mathrm{1}}-x_{i,j,\mathrm{2}}$, where x_i,j,1 is the standard deviation of the ith model's jth mode for the first 50-year segment of the piControl simulation. A map with the spatial extent of these modes is given in Fig. S1 in the Supplement.

2.7.1 Local variability

Local variability is computed as the standard deviation of the annual mean temperature or precipitation. In all simulations, a 50-year subset was selected (typically the final 50 years; Sect. 2.5), and anomalies with respect to the simulation climatology were computed and then detrended. Standard deviation ratios were computed on the individual model grids and interpolated bilinearly onto a common 1×1^∘ latitude–longitude grid prior to ensemble averaging.

2.7.2 The El Niño–Southern Oscillation (ENSO)

The El Niño–Southern Oscillation (Bjerknes, 1966) is an atmosphere–ocean coupled mode of variability with large-scale changes in SST, SLP, precipitation, and winds as well as the ocean thermocline depth in the equatorial Pacific varying semi-periodically with a timescale of 2–10 years (Philander, 1983). ENSO is one of the main drivers of global mean temperature variability, with global teleconnections (Bjerknes, 1969) and a pronounced impact on the global energy balance and global mean temperature (Trenberth and Fasullo, 2012; Foster and Rahmstorf, 2011). The SLP oscillation in the South Pacific (“Southern Oscillation”) was first described by Walker and Bliss (1932), and the link between atmospheric oscillating patterns and local ocean circulation was first described by Bjerknes (1966). Here we use the Niño3.4 and Niño4 indices, which are the equatorial (5^∘ S–5^∘ N) area-averaged SST anomalies over the regions 170–120^∘ W and 160^∘ E–150^∘ W, respectively (Trenberth, 1997; Deser et al., 2010, 2012b).

2.7.3 The Interdecadal Pacific Oscillation (IPO)

The Interdecadal Pacific Oscillation (IPO) shows a pattern of SST change similar to ENSO (equatorial warming), but with different impacts (Power et al., 1999; Meehl and Hu, 2006). Here we construct a monthly index time series based on the first principal component of 13-year low-pass-filtered Pacific (40^∘ S–60^∘ N, 110^∘ E–70^∘ W) area-weighted SST anomalies, from which the global mean SST anomaly has been removed at each time step.

2.7.4 The Indian Ocean Dipole (IOD)

The Indian Ocean Dipole (IOD) is an irregular pattern of SST variability in the Indian Ocean independent of ENSO in the Pacific (Webster et al., 1999). In a negative IOD event, the western region warms and eastern region cools. The opposing pattern, with a decrease in the zonal temperature gradient, is a positive IOD event. The associated changes in surface pressure and rainfall lead to rainfall modulation and extreme precipitation events at the western–eastern boundaries (Webster et al., 1999). Its subdecadal variability is modulated on decadal to multidecadal timescales (Ashok et al., 2004). Here, the index time series is calculated as the difference of the area-averaged SST anomaly between the regions 50–70^∘ E, 10^∘ S–10^∘ N, and 90–110^∘ E, 10^∘ S at the Equator (Saji et al., 1999).

2.7.5 The Atlantic Meridional Mode (AMM)

The Atlantic Meridional Mode (AMM), sometimes called the Atlantic dipole mode or gradient mode, is a leading mode of SST variability in the equatorial Atlantic (Servain et al., 1999). The SST pattern, with opposing anomalies on either side of the Equator, modulates the meridional gradient of the sea surface temperature anomaly in the tropical Atlantic and hence the movement of the Intertropical Convergence Zone (ITCZ) and associated precipitation (Xie and Carton, 2004). The SST gradient is complemented by cross-equatorial atmospheric flow, strengthened by wind–evaporation–surface temperature feedbacks (Xie and Carton, 2004). The AMM has been linked to hurricane activity in the area (Vimont and Kossin, 2007) and impacts rainfall over the tropical Atlantic, NE Brazil, and the Sahel (Kushnir et al., 2006). Following Doi et al. (2010), the AMM state is defined here as the area average, detrended SST anomaly difference between the two regions 15–5^∘ N, 50–20^∘ W and 15–5^∘ S, 20^∘ W–10^∘ E (Phillips et al., 2014).

2.7.6 The Atlantic Zonal Mode (ATL3)

Atlantic Zonal Mode (ATL3) is an equatorial coupled mode similar to ENSO (Zebiak, 1993), and it is therefore sometimes referred to as “Atlantic Niño” (Xie and Carton, 2004). Calculation of the mode in the CVDP follows Zebiak (1993) and is based on the area average of the detrended SST anomaly over the region 3^∘ N–3^∘ S, 20–0^∘ W. The ATL3 displays interannual variations with roughly a 4-year period. Its variations are linked to rainfall variability in the Sahel region (Giannini et al., 2003).

2.7.7 The Pacific Decadal Oscillation (PDO)

The Pacific Decadal Oscillation (PDO; Power et al., 1999) is the leading mode of variability in monthly SST anomalies over the North Pacific after the global mean anomaly is removed. It emerges as a mode partially driven by ENSO and independent, stochastically emerging variations with a timescale of decades (Mantua et al., 1997; Deser et al., 2010; Schneider and Cornuelle, 2005). However, no clear spectral peak has been identified (Deser et al., 2010), as it arises from a superposition of SST fluctuations with different dynamical origins (Schneider and Cornuelle, 2005). The PDO was first described in 1997 as a recurring climate pattern of ocean–atmosphere variability over the North Pacific linked to impacts on salmon production and coastal surface temperatures on the west coast of the North American continent and the adjacent sea surface (Mantua et al., 1997). The index is associated with temperature and precipitation changes over the western and eastern edges of the North Pacific and displays a positive correlation with winter precipitation in California (Mantua et al., 1997). The pattern is generally similar to ENSO variations but with a weaker southern Pacific imprint (Deser et al., 2010). We calculate a monthly index time series from the leading principal component of the area-weighted SST anomalies in the box 20–70^∘ N to 110^∘ E–100^∘ W, from which the global mean SST anomaly for each time step has been removed (Deser et al., 2010).

2.7.8 North Atlantic Oscillation (NAO) and the Northern Annular Mode (NAM)

The North Atlantic Oscillation (NAO) is a quasi-periodic spatial pattern of sea level pressure changes between the Arctic and subtropical North Atlantic (Stephenson et al., 2003; Walker and Bliss, 1932). NAO variations impact the atmospheric circulation over the North Atlantic and the strength of the westerly inflow into Europe, influencing storm tracks, temperature, and precipitation, in particular in boreal winter (Hurrell, 1995; Hurrell and Deser, 2010). It varies on a seasonal, interannual, and decadal timescale (Hurrell, 1995). In positive NAO phases, a large difference in SLP between the high latitudes and midlatitudes implies a strong SLP gradient and strong westerly inflow into central Europe. In negative NAO phases, the smaller difference in pressure is associated with a southerly shift in the North Atlantic storm tracks and enhanced precipitation in the Mediterranean and North Africa. Here we calculate the NAO index based on the first principal component of the boreal winter (DJF) area-weighted sea level pressure in the box 20–80^∘ N, −90 to 40^∘ E (Hurrell and Deser, 2010). Given that this calculation results in a normalized time series, to investigate changes in NAO variability, we consider the spatial standard deviation of the empirical orthogonal function (EOF) over the box instead (Power et al., 2013).

The Northern Annular Mode (NAM) describes deviations in the zonal pressure gradient between the polar regions and the subtropics. This gradient governs the synoptic (5 d mean) variability of sea level pressure in the NH (Lorenz, 1951). By definition, it is related to the NAO. Here, it is calculated as the leading EOF of the area-weighted monthly mean SLP anomalies over the latitudes 20–90^∘ N (Hurrell and Deser, 2010), with its variability measured by the spatial standard deviation of this EOF (Power et al., 2013).

2.7.9 Southern Annular Mode (SAM)

The Southern Annular Mode (SAM) index gives the strength of the sea level pressure gradient in the Southern Hemisphere midlatitudes (Karoly, 1990). It is a distinctive pattern of climate variability in the Southern Hemisphere, in particular in winter (Karoly, 1990; Marshall, 2003). Variations in the SLP gradient impact regional temperatures, precipitation (Marshall, 2003; Gillett et al., 2006), and the circulation of the Southern Ocean. Negative values of SAM have been linked to weakenings of the polar vortex and an increasing occurrence of hot and dry extremes in Australia (Lim et al., 2019). SAM impacts latitudinal rainfall distribution from the subtropics to Antarctica, with recent trends towards a more positive mode than over the last 1000 years, and is linked to an Antarctic interior cooling and peninsula warming (Abram et al., 2014). Monthly PSL anomalies averages are formed over the latitudes 20–90^∘ S, and a square root of the cosine of latitude weighting is applied. The leading EOF is considered to give the pattern for the SAM (Thompson and Wallace, 2000), and the spatial standard deviation of this pattern (Power et al., 2013) is used as our measure of its variability.

2.8 Changes in precipitation extremes

We investigate the major large-scale patterns associated with precipitation variability across climates. Based on Fig. 3 we find that, in many regions, past and future precipitation variability shows opposing signs. We select five regions with Mediterranean-type climates (Seager et al., 2019): (1) the southwestern tip of South America, (2) southwestern South Africa, (3) southwestern Australia, (4) coastal western North America, and (5) the western Mediterranean. At present, these regions lie between the poleward edge of the winter Hadley cell and equatorward edge of the midlatitude storm tracks. The climate is therefore characterized by wintertime precipitation and summertime dryness associated with subtropical subsidence; it displays substantial interannual variability (Seager et al., 2019).

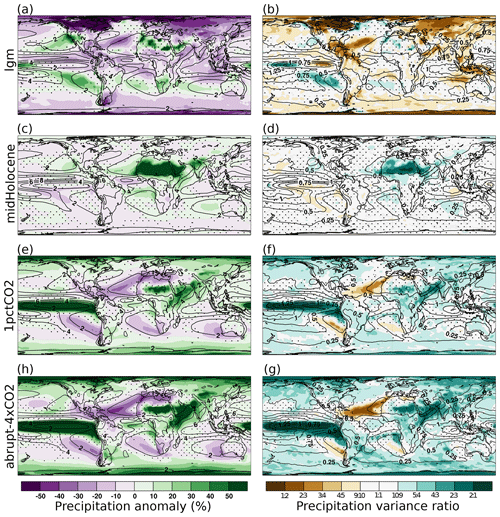
Figure 3 The change in mean annual precipitation (a–d) and its variability (e, f) across multiple climate experiments. Each panel shows the ensemble average difference (as percentage changes with respect to each model's piControl). The changes in variability are based on the ratio of the standard deviation of annual mean precipitation in the experiment to that of the piControl experiment. Ratios above 1 indicate higher variability in the experiment than in the piControl. The contours in each panel show the ensemble mean pattern in the preindustrial control (mm d⁻¹). Contour variations are due to the different number of models available for individual experiments, as the preindustrial ensemble mean is only computed from models in each experiment. Stippling indicates where the sign of the change disagrees for more than two-thirds of the ensemble.

For each region, model, and experiment we first calculate the climatological average, annual mean precipitation, and, as an individual threshold, the interannual standard deviation of local precipitation. We then identify where, in the 50-year time slice, precipitation falls above or below 1 SD (standard deviation), and composite sea level pressure, surface air temperature, and precipitation for these extreme precipitation years across all experiments and model simulations.

2.9 Timescale dependence of the variability changes

The power spectrum, P(τ), of a climate variable describes how its variability is distributed over the timescales τ, with the integral over the entire spectrum yielding the total variance of the signal (Chatfield, 2004). Here we use a multitaper power spectrum (Thomson, 1990) with linear detrending and investigate the area-weighted mean spectra of the local (grid box) time series. The scaling exponent, β, is used to summarize the scaling relationship of variance with timescale or equivalently frequency, which relates to the timescale as $f=\mathrm{1}/\mathit{\tau }$, assuming that the spectrum approximately follows P(f)∼τ^β. The scaling exponent β is estimated as the linear slope between the logarithm of the power spectral density and the logarithm of timescales; the fit is performed between 4 months to 20 years. Uncorrelated white noise has no autocorrelation, and the scaling exponent is zero (β=0). For β>0 (β<0), the underlying stochastic process displays positive (negative) autocorrelation. Positive autocorrelation for temperature can be expected (Fredriksen and Rypdal, 2016), while precipitation and pressure have lower or negative values (Fraedrich et al., 2009).

3 Results

3.1 Hydrological sensitivity across the ensemble

Figure 1 shows the range of global mean temperature change and precipitation change from the piControl simulations. The lgm ensemble has a mean temperature anomaly of 4.2 K (range of −2.5 to −6 K), and precipitation anomalies range from −6 % K⁻¹ to −12 % K⁻¹. The midHolocene ensemble shows no large, consistent global mean changes. However, models with wetter conditions show positive global mean temperature anomalies. The 1pctCO2 simulations display temperature anomalies from +3 to +7 K, and precipitation increases between 3 % and 12 %. The abrupt4xCO2 warming simulations are slightly warmer (+4 to +7 K) and wetter (+5 to +12 % K⁻¹). For the entire ensemble, we estimate an overall mean HS of 1.73±0.005 (1 standard error of the slope), taking into account all models weighted equally. The equilibrium experiments (lgm and midHolocene) fall consistently on the 2 % K⁻¹ line (Allen and Ingram, 2002), whereas the transient warming experiments fall below. We find no discernible difference in the precipitation scaling between the CMIP5 and CMIP6 models. We find no systematic relationship between each model's equilibrium climate sensitivity (ECS) and HS. Additional investigations (not shown) demonstrate that our findings hold with and without calendar adjustment.

3.2 Changes in local interannual variability

We aim at a comparison of mean state and variability changes across multiple climate states. Changes in temperature and temperature variability (Fig. 2) do show some consistent progression from the paleoclimate experiments to the idealized warming. As expected, we find globally cooler conditions for the LGM. These are highly consistent across the ensemble, as there is scarcely any stippling in Fig. 2a, indicating that at least two-thirds of the considered models agree on the same sign as the mean. Comparing this to Fig. 2e, which shows the change in simulated temperature variability in the lgm experiment vs. the piControl as the ratio of the standard deviations of the annual means, shows that the interannual temperature variance is high in areas that experienced much colder conditions (at the sea ice edges) and where the lower sea level led to more exposed shelves (e.g., Indonesia) as well as at the edges of the large continental ice sheets (Laurentide and Eurasian). The simulated lgm temperature variability is higher in the middle to high latitudes of both hemispheres, but large areas of the tropics show decreases in interannual temperature variance against the piControl experiment, in particular the ENSO region, South America, southern Africa, and the West Pacific Warm Pool. Overall, the mean change pattern of the lgm experiment is weakly anticorrelated with the pattern of standard deviation changes ($r=-\mathrm{0.12}$ and p<0.05 based on area-weighted Pearson correlation and a one-sided t test, conservatively assuming 500 degrees of freedom and accounting for the high degree of spatial autocorrelation in the fields).

The local changes in mean precipitation for the lgm simulations (Fig. 3a) are overall negative, consistent with the globally decreased precipitation (Fig. 1). We find consistent shifts towards higher precipitation in the continental areas of both hemispheres affected by subtropical subsidence precipitation: over northern Africa, southern Africa, across the subtropical southern Atlantic, and southwestern North America. Interannual precipitation variance in the lgm simulations is lower than in the control simulations with the exception of the areas that have higher mean precipitation, for which variability also increases (Fig. 3e). Across the multimodel field, mean and standard deviation changes are positively correlated (r=0.63, p<0.01).

The midHolocene simulations show weak but consistent (sub)tropical cooling and moderately warmer conditions in the annual mean temperatures (Fig. 2b), as expected given the positive high-latitude insolation forcing (Sect. 2.3). Overall, the interannual temperature variance shows patterns of higher- and lower-than-piControl variance with modest degrees of inter-model consistency. Similar to the lgm variance ratio field, there are reductions in the tropical Atlantic temperature variance, colocated with a local increase in precipitation (Fig. 3b), and precipitation variance (Fig. 3f). Precipitation variance appears lower in the Pacific and higher over the Atlantic and Indian Ocean sector, with a strong positive precipitation anomaly over northern Africa. Mean and standard deviation changes are strongly correlated for precipitation (r=0.55, p<0.01) but only weakly correlated for temperature (r=0.09, p<0.05).

Mean temperature change for the 1pctCO2-scenario is consistently positive, with stronger warming over the continents and amplified warming in the high northern latitudes (Fig. 2c). The interannual temperature standard deviation ratio (Fig. 3g) shows consistent increases in temperature variability over southwestern North America, South America, Africa, Australia, the Indian Peninsula, and China, as well as over the North Atlantic and decreases in temperature variability against piControl over northern North America, Scandinavia, the Tibetan Plateau, northeast China, and across the Arctic. Surrounding Antarctica, decreasing temperature variability is observable south of the polar circle, but moderate increases in temperature standard deviations are observable over East Antarctica. Overall, the mean change and standard deviation change patterns are anticorrelated ($r=-\mathrm{0.23}$, p<0.01), meaning that where we find stronger warming we also observe lower simulated temperature variability.

Mean precipitation change across the 1pctCO2 ensemble is positive (Fig. 1). However, inspecting Fig. 3 indicates that this increase primarily affects the high latitudes and the equatorial region. In South America, no clear change in precipitation is discernible, whereas the Sahel and Arabian Sea are wetter. Mean and standard deviation change fields are positively correlated (r=0.67, p<0.01). Patterns of temperature and precipitation changes in the abrupt4xCO2 scenario (Figs. 2d and 3d) are highly consistent with those for the 1pctCO2 scenario (r=0.94, p<0.01 for precipitation; r=0.98, p<0.01 for temperature). In mean and variability, a stronger amplification of the warming patterns (Fig. 2h) over the continents, the North Atlantic, the Indo-Pacific, and the locations of the subtropical high is discernible. The polar and continental amplification of the temperature change patterns in the lgm scenario is mirrored in the areas of warming in the 1pctCO2 and abrupt4xCO2 scenarios ($r=-\mathrm{0.65}$ and $r=-\mathrm{0.64}$, respectively; p<0.01). In particular in the west coast midlatitudes, where higher precipitation is simulated at the LGM, it appears lower in the warming scenarios of the NH.

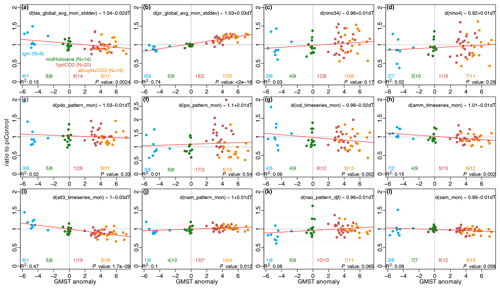
Figure 4 Relationship of the standard deviation of climate indices and modes to the change in global mean temperature from preindustrial conditions. Colors indicate the different experiments: CMIP5 and CMIP6 models are not differentiated. (a) Change in the standard deviation of the global annual mean surface temperature. (b) Change in the standard deviation of the global annual mean precipitation rate. Changes in the standard deviation (i.e., amplitude of the mode) of (c) ENSO based on the Niño3.4 index and (d) based on the Niño4 region, (e) the PDO, (f) the IPO, (g) the IOD, the meridional (h, AMM) and zonal (i, ATL3) modes of equatorial Atlantic SST variability, (j) the Northern Annular Mode, (k) the boreal winter NAO, and (l) the Southern Annular Mode. Dashed horizontal lines are given from $\mathrm{1}\pm \mathrm{2}{\mathit{\sigma }}_{\mathrm{int},\mathrm{mode}}$. See Sect. 2.7 for details on the individual modes and how changes in the mean state between the experiments are removed prior to calculation. Linear unweighted fits to the mode changes are given in each panel without censoring for significance. P values assume 60 degrees of freedom.

3.3 Changes in modes of variability

3.3.1 Changes in the global mean

Global mean precipitation increases with global mean temperature across the ensemble (Fig. 1). However, the variance of global mean temperature decreases with the global mean state, resulting in lower variance than in the piControl for the majority of models considered in the idealized warming scenarios and higher-than-preindustrial variance for the lgm experiment (Fig. 4a). At the same time, the standard deviation of global mean precipitation increases at approximately 3 % K⁻¹ (Fig. 4b), hence at a higher rate than the global mean precipitation (Fig. 1). Comparing these temporal changes against the spatial expression in Figs. 2 and 3, we find that the global reduction of temperature variability with warming is dominated by the ocean and high-latitude signal, whereas the midlatitude continental areas show consistent increases in temperature variability with warming. At the same time, the increase in precipitation is more inhomogeneous in spatial location and magnitude (Fig. 3d and h).

3.3.2 Changes in SST-based modes

Changes in the SST-based modes of variability across the ensemble are given in Fig. 4c–h. The majority of models (6∕9) show a lower-than-preindustrial Niño3.4 and Niño4 standard deviation for the lgm and for the midHolocene (9∕14), as well as a higher-than-preindustrial ENSO index variance for the idealized warming scenarios (8∕10 and 7∕11; Fig. 4c and d). Nonetheless, there is no statistically significant link between global mean temperature and ENSO variability increase (e.g., Christensen et al., 2013). Preliminary findings from the new PMIP4 simulations appear to confirm these conclusions about the paleoclimate time periods (Brown et al., 2020). This fits with paleo-ENSO reconstructions of suppressed activity during the mid-Holocene, yet with potential changes in ENSO variability during the LGM (Lu et al., 2018). There are no systematic changes in standard deviation across the ensemble for the PDO (Fig. 4e) or the IPO (Fig. 4f), although both are not well resolved by the short records analyzed here. For the IOD (Fig. 4g) there are no tendencies in the lgm ensemble, with about as many models showing an increase in standard deviation as showing a decrease. However, a majority of models show suppressed IOD activity under the warming scenarios corresponding to the reduced temperature variability over the Arabian Sea upwelling (Fig. 2), which may be a response to the increased ocean stratification seen in the transient simulations (Oyarzún and Brierley, 2019). In the tropical Atlantic, weak but negative trends for the AMM (Fig. 4h) and the ATL3 (Fig. 4i) variability for warmer conditions are found. This fits with the findings of Brierley and Wainer (2018) and is not inconsistent with the increased future rainfall variability over both the Amazon and western Africa (Fig. 3g and h) – rather, it indicates a diminished influence of Atlantic climate variability in the regions.

3.3.3 Changes in atmospheric modes of variability

Let us now consider the atmospheric modes of variability (Fig. 4j–l). In the lgm experiments, the simulated temperature gradient in the NH is higher than in the piControl – all but one model (Fig. 4) show reduced variability for the NAM and the NAO. Conversely, in the idealized warming scenarios, which have a reduced meridional temperature gradient, more models show increasing standard deviations. Whether a reduced standard deviation indicates a more stable storm track or a more spatially constrained one requires further investigation and possibly moving away from EOF-based mode definitions.

The Southern Annular Mode shows a tendency towards reduced standard deviations for the idealized warming scenarios (Fig. 4i). This also occurs in the lgm experiments. This counterintuitive response may arise from the competing influences of variability of the Antarctic sea ice edge (Fig. 2) and the hydrologically related variability within the storm tracks (Fig. 3).

3.4 Circulation patterns underlying extratropical precipitation extremes

Precipitation changes in Mediterranean-type climates on the western edges of continents in the extratropics display opposite signs in their precipitation anomalies, with respect to preindustrial and relative to the global mean change across the ensemble (see Fig. 5). Given this difference, we assess whether the atmospheric drivers of such regional precipitation are consistent from past to future climates to better inform the relevance of variability in paleoclimates to future climate change in these susceptible semiarid regions. We investigate sea level pressure and surface air temperature anomalies associated with high and low annual precipitation by compositing over years with regional precipitation above or below 1 standard deviation around the mean (following Sect. 2.8). Exploratory investigations uncovered no statistically significant changes between individual climate states (not shown). The following proceeds by the regions in Fig. 5.

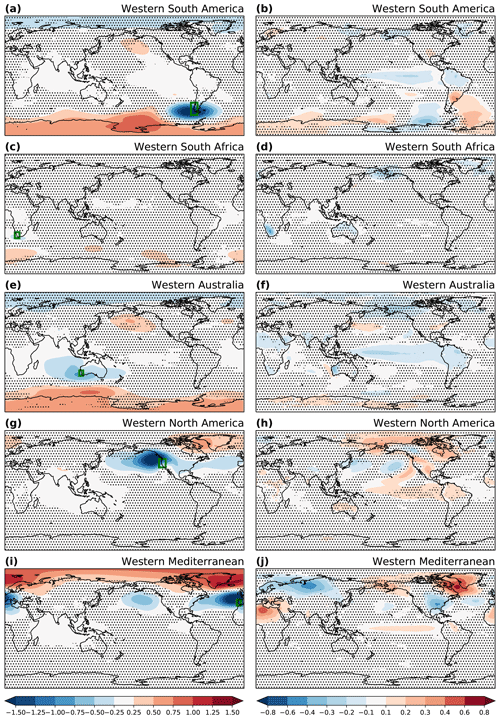
Figure 5 Sea level pressure (hPa) and surface air temperature (^∘C) anomaly composites for high precipitation years in five regions with Mediterranean climates (indicated by green boxes in the left-hand panels). Sea level pressure anomaly composites (a, c, e, g, i) and surface air temperature anomaly composites (b, d, f, h, j) show the large-scale patterns across models and experiments composited over years of anomalously high precipitation (defined as 1 standard deviation above the average) in each region. Stippling shows areas where fewer than two-thirds of the simulations agree on the sign of the pattern. Figures S2 and S3 show the corresponding composites for anomalously low precipitation and composites for the precipitation change in these years.

High precipitation years in southwestern South America (Patagonia) are associated with an increased SLP gradient between the region and the Antarctic continent (Fig. 5a), indicative of positive SAM conditions, a moderate cooling in the southeastern Pacific sector, and warmer conditions in the South Atlantic and southern Indian Ocean. The reverse situation can be found for years with low precipitation anomalies in the same region (Fig. S2a and b). This is true for the entire ensemble (Fig. S3) and for individual climate states (not shown). The global precipitation composites for regional high and low precipitation years in Fig. S3 show that years with high precipitation anomalies in the region are also associated with lower-than-average precipitation in the ENSO regions (Fig. S3b).

There is no inter-model and inter-experiment consistency in the interannual atmospheric conditions for high precipitation years in western South Africa with regards to SLP and temperature (Fig. 5c and d), indicating that the drivers of variability are more complex in this region and cannot be explained by a single climate mode. Precipitation variability may therefore be more controlled by differences between individual storms than by persistent large-scale modes of the atmosphere. Indeed, there are no coherent large-scale structures even within individual climate states, though a regional signature in temperature exists (Figs. S2 and S3).

The composite plots for southwestern Australia (Figs. 5e, f, S2 and S3) show, similarly to the southwestern South American composites, that increased precipitation is found for years with a strong SAM and an increased SLP gradient between Australia and Antarctica. The higher pressure and temperatures in the North Pacific sector for both southwestern South American and western Australian composites could indicate stable teleconnection patterns across the experiments. Cooler conditions prevail throughout the tropics in high precipitation years, suggesting a decreased Southern Hemisphere meridional temperature gradient. Precipitation composites (Fig. S3e and f) show a dipole-like structure reminiscent of ENSO, with more precipitation in western Australia associated with increased precipitation in southeast Asia and less-than-average precipitation in the equatorial Pacific.

High precipitation in southwestern North America is associated with enhanced local low pressure and higher-than-average SLP over the eastern North Pacific, the North Atlantic, and Greenland (Figs. 5g and S2), as well as locally warmer conditions (Figs. 5h and S3) and drier conditions to the north and south (Alaska and Mexico; Fig. S3h). These patterns suggest a consistent influence of the PDO and the NAM on interannual precipitation variability in the region.

This response is structurally highly similar to the patterns observable for the western Mediterranean, where high precipitation anomalies are associated with an increased pressure gradient between the middle and high latitudes (Figs. 5i and S3), cooler conditions on the Iberian Peninsula and Eurasia, and warmer conditions over the Arctic regions of North America and the Labrador Sea (Figs. 5j and S3). For both western North America and the western Mediterranean, high annual precipitation years are associated with positive precipitation anomalies in the equatorial Pacific (Fig. S3h and j).

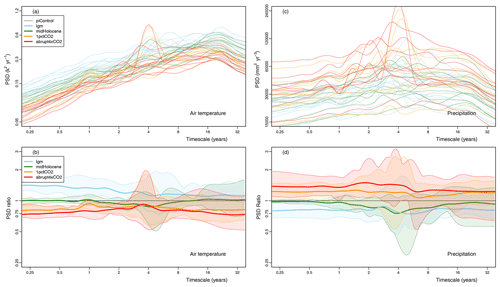
Figure 6 Changes in the global mean of the power spectra between the experiments. For temperature (a), variance across all timescales and for most models is highest in the lgm experiment and decreases for the warmer experiments. This is the opposite for precipitation (c), which sees moderate increases in precipitation variability with warming. For each model, we took the ratio of the global mean spectra of each experiment to the piControl for both temperature (b) and precipitation (d), thus showing the timescale dependency of the local variance change. Shaded confidence intervals are based on the entire range of the model ratios.

In summary, in both southwestern South and North America, anomalous precipitation is associated with sea level pressure variations over the eastern Pacific in the respective hemisphere (low pressure during wet years and high pressure during dry years) illustrative of circulation patterns that are more or less conducive to water delivery to the continent. In the Southern Hemisphere, this is also associated with a standing wave structure in surface air temperatures at midlatitudes and an equatorial Pacific signature reminiscent of ENSO. Precipitation variability over southwestern Australia is also linked to equatorial Pacific temperatures, as well as pressure variations in the Indian and South Pacific oceans, while precipitation variability over the western Mediterranean is more strongly linked to variability over the North Atlantic (likely the NAO), as well as the North Pacific and eastern equatorial Pacific (the latter is suggestive of ENSO).

3.5 Changes in the spectrum of variability

We investigate the globally averaged, area-weighted power spectra of local monthly temperature (Fig. 6a and b) and precipitation (Fig. 6c and d) anomalies. We find that, in the global mean, the spectrum of temperature shows overall higher local temperature variability in the lgm experiments and lower temperature variability for the warm experiments (Fig. 6a), consistent with the findings for total variance (Figs. 2, 3 and 4a, b). On the ENSO timescale (around 3–7 years), the reduced variance is less important for the warm experiments but more important for the midHolocene experiment, thus leading to small changes in the variance on longer and shorter timescales. Overall, the scaling of intra-annual to decadal temperature variability is consistent for all experiments (ranging from β=0.26 to β=0.35). The scaling changes little with respect to the piControl experiment, as can also be seen by the relatively flat spectral ratio curves (Fig. 6b). The lgm curve, however, shows a small decrease in scaling since the variance increases more on smaller timescales. There is also an annual peak in the 1pctCO2 temperature spectra, which could be due to an incomplete detrending of a changing seasonal cycle. The global picture of more variable surface temperatures in the lgm experiments and decreased variance at all timescales for the warmer experiments is weakened over land (Fig. S6) but holds over the oceans (Fig. S7). However, temperature variance increases over low-latitude to midlatitude continental areas in the warm experiments (Fig. S8, spectrum across 40^∘ S to 40^∘ N). Generally there is no strong inter-model consistency over the low-latitude to midlatitude continental areas, as also indicated by Fig. 2.

The variance around the 3–5-year timescale in the warm experiments is more apparent for the local precipitation anomalies than for temperature (Fig. 6c); this is consistent with the findings of Cai et al. (2014), who found an increasingly frequent ENSO occurrence in warming experiments. Conversely, we find that it also decreases for the midHolocene and lgm experiments. Overall, the precipitation variance increases fairly consistently over all timescales for the warm experiments with respect to the piControl runs and likewise decreases for the lgm and midHolocene experiments. The precipitation spectral ratios with respect to the piControl simulations (Fig. 6d) outline these patterns. These coherent changes in the global mean spectra are also corroborated by a high degree of consistency in the scaling patterns of surface temperature, precipitation, and surface pressure (Fig. S4), which show “white”, or flat, spectra over the continents and “red” spectra with variance concentrated at longer timescales over the oceans, particularly along the Equator. There is a reddening of the variability over areas where sea ice is lost in the warm experiments. This could be attributed to the open seas dampening the high-frequency variability more with warming. There is a similar blueing in the lgm over the Fram Strait and the Barents Sea where sea ice cover is extended (Fig. S4). However, there is a reddening over the Arctic for sea level pressure in the lgm.

4 Discussion

4.1 Changes in climate variability with global mean temperature

Using a wide range of model simulations has allowed us to examine the relationship between changes in global mean temperature and climate variability from the perspective of the mean and standard deviation fields, changes in modes of variability, and the timescale dependency of temperature and precipitation changes. We find that globally averaged temperature variability decreased from the cold to the warm climate states. We also find that consistent changes in temperature variance are more localized than changes in the mean fields. From the cold to the warm(er) simulations, temperature variability increases over land and tends to decrease over the oceans. This pattern also holds across timescales. Temperature variability reduction is particularly strong at high latitudes, where seasonality and interannual temperature variability are high (Huybers and Curry, 2006). This suggests that changes in temperature variability, in both directions, affect areas that also undergo a large mean state change.

We find clear indications for relationships between global mean temperature and precipitation variability as well as in modes of variability in the tropical Atlantic, with the zonal and meridional modes both strongly varying in the lgm experiments and shifting towards weaker variability in the warmer scenarios. This is consistent with the recent findings of Brierley and Wainer (2018), who investigated tropical Atlantic sea surface temperature variability using a similar model ensemble but also including the historical era. The zonal gradient mode in the Indian Ocean, IOD, shows a tendency for lower variability in the midHolocene (and thus for tropical weak cooling) and future warming scenarios, and it is therefore not systematically changing with global mean temperature.

The reduced ENSO variability for the midHolocene experiments shows that the strength of ENSO primarily links to the tropical temperature changes and secondarily to global mean temperature change. This finding is corroborated by a clear decrease in ENSO-related variance in the global mean spectra for the midHolocene experiments. Beyond the ENSO-related timescales, however, changes in temperature and precipitation variability scale across the experiments without strong regard for timescales. In the ENSO power spectral range of 3–7 years we notice a peak-and-trough pattern of some models, which might represent a change in the ENSO frequency impacting global-scale climate variability. Changes in ENSO spatial patterns or the event amplitude, however, would not be visible in the spectrum if the overall variance at the timescale did not change. Previous studies have suggested that ENSO variability might increase with global warming (e.g., Cai et al., 2018; Timmermann et al., 1999), but we do not find clear evidence supporting this finding (in agreement with Brown et al., 2020).

The meridional atmospheric gradient modes of variability in both hemispheres (SAM, NAM, and NAO) show a weak tendency towards more positive (poleward) displacements of the subtropical high with global mean temperature increase. This is consistent with the findings of precipitation reductions in Mediterranean climates at the western continental edges in both hemispheres. However, it is unclear to what extent the annular mode (and the westerly jet position) shift is due to changes in global mean temperature and general circulation or due to ice sheet height and sea ice changes that might, to some extent, be independent of the change in the mean (Chavaillaz et al., 2013).

4.2 Temperature vs. precipitation scaling

Global averaged precipitation variability increases with the global mean temperature of the experiments in our analyses (Figs. 2, 3 and 4b). There is a larger degree of correlation between mean and variability change for precipitation: dry regions in the lgm experiment are spatially extensive and highly correlated with areas of lower precipitation variability (Fig. 3). Conversely, wetter regions in the idealized warming scenarios also show higher precipitation variability. Yet, we find no relationship between the propensity of a model for precipitation increase and its sensitivity to warming under increased GHG forcing (Table 1). The overall scaling of 1.7 % K⁻¹ found across the model ensemble is somewhat lower than the 2 % K⁻¹ Li et al. (2013) found for a similar (although smaller) set of CMIP5 models and experiments. This is also smaller than what has been established for earlier models (Allen and Ingram, 2002; Held and Soden, 2006). We note, however, that mean precipitation in the lgm – to midHolocene – experiments scales with the respective temperature anomalies by 2 % K⁻¹, and it is the idealized transient warming scenarios that fall below these lines. This could indicate that the temperature in these experiments changes faster than precipitation responses and, if the experiments are continued, would get closer to the expected line (Samset et al., 2018; Myhre et al., 2018; Andrews et al., 2010). Indeed, Samset et al. (2018) found that the precipitation increase over the global oceans is markedly slower than that over land, which perhaps explains why our scaling is closer to the terrestrial response in equilibrium experiments (1.8 % K⁻¹; Li et al., 2013). Andrews et al. (2010) established that the atmospheric response correlates strongly with the radiative forcing, whereas the slow response is independent of the mechanism leading to the global temperature change of 2 % K⁻¹–3 % K⁻¹. It is also unclear how precipitation variability relates to precipitation extremes, as they typically operate on much shorter timescales. O'Gorman et al. (2011) found, based on CMIP3 model simulations, that extratropical precipitation extremes increase at 6 % K⁻¹ and hence at a rate closer to the thermodynamic rate of 7 % K⁻¹ (Allen and Ingram, 2002; Held and Soden, 2006). Global mean precipitation rates are therefore increasing with warming. At daily to interannual timescales, soil moisture plays a relevant role in the precipitation feedback on temperature variability (Vidale et al., 2007; Fischer and Knutti, 2013). It is, however, also clear that models have difficulties representing these feedbacks at the land surface, in particular on longer timescales (Rehfeld and Laepple, 2016). The detailed representation of subgrid-scale convective processes could also determine whether a local feedback is modeled positively or negatively (Hohenegger et al., 2009). The observed negative coupling between local temperature and precipitation variability at short timescales (e.g., Trenberth and Shea, 2005, found local correlations up to −0.7) should therefore feed back onto higher temperature variability, but we cannot assess to what degree from this analysis, as synoptic-scale processes are not resolved in the monthly data available.

4.3 Comparison to climate reconstructions and observations

Analysis of instrumental records has shown that the number of record-breaking rainfall events has been increasing over the instrumental era (Lehmann et al., 2015). This is consistent with an ongoing increase in the global mean precipitation rate. Evidence for continental-scale colder and drier conditions at the LGM comes from a variety of terrestrial proxies (Kohfeld and Harrison, 2000; Bartlein et al., 2011) and oceanic proxies (MARGO project members, 2009). The sampling rate and resolution of proxies for paleohydrology are, however, often not sufficient to investigate changes in precipitation variability. A high-resolution speleothem record allowed Luetscher et al. (2015) to relate shifts in the LGM to westerly storm tracks in Europe, which is consistent with our finding of enhanced precipitation in the lgm experiments. Koutavas and Joanides (2012) suggested that ENSO variability was higher at the LGM than in the Holocene. It is, however, unclear how this relates to our finding of more La Niña-like conditions in most model simulations, but a reduced variance in ENSO3.4-region SSTs has been corroborated by isotope proxies and isotope-enabled modeling (Zhu et al., 2017). Other studies found ENSO variability to become more persistent with GHG-induced warming (Cai et al., 2014), especially for precipitation. Our results suggest that mean state and variability changes are coupled for both temperature and precipitation. Notwithstanding methodological challenges (Rehfeld et al., 2016; Rehfeld and Laepple, 2016), if robust joint and/or colocated estimates of past temperature and precipitation can be obtained from proxy data, these could potentially serve as constraints on future projections (Schmidt et al., 2014).

4.4 Limitations

We have shown that patterns of temperature and precipitation variability in paleoclimate and future simulations mirror one another, bringing together equilibrium and transient experiments. Nevertheless, there are important limitations that preclude a direct interpretation for future projections (Christensen et al., 2013). Firstly, the snapshots we analyzed here are short (50 years), and therefore many slower modes of variability operating on decadal or longer timescales are difficult to assess (such as the IOD or the PDO). Furthermore, we are not able to investigate the variability in the index time series but only their mean strength. Analysis of multidecadal modes, and driving mechanisms of variability changes (e.g., from the ocean circulation or sea ice mechanisms) in future studies could provide critical insights and would strongly benefit from the availability of stored model diagnostics (e.g., AMOC strength) and longer simulation output. We have limited the analysis to linear properties of the surface climate fields and therefore cannot distinguish whether local changes are remotely forced, e.g., due to changing teleconnections from ENSO. We find that, while temperature variability decreases in the model simulations from the lgm to the future 1pctCO2 and abrupt4xCO2 scenarios, the magnitude of change is far lower than that observed in proxy data on longer timescales (Rehfeld et al., 2018). This could be due to models underestimating regional variability beyond the multidecadal timescale (Laepple and Huybers, 2014b; Rehfeld et al., 2018). At the global scale, climate models do, however, capture correct levels of intra-annual to multidecadal temperature variability (Laepple and Huybers, 2014a; Pages2k-Consortium, 2019).

5 Conclusions

We have investigated the simulated changes in surface climate variability across a wide range of climates based on the PMIP3–CMIP5–CMIP6 model ensembles. We find global patterns of changes that are roughly opposite between cold (lgm) and warm (1pctCO2 and abrupt4xCO2) experiments. Simulated global mean precipitation is found to increase with global temperatures. This is true for the change from preindustrial conditions to idealized CO₂-induced warming scenarios. We also find a similar increase from the cold period of the LGM to the preindustrial reference period. Simulated temperature variability is, at the global scale, higher in the lgm scenarios and decreases with temperature. Precipitation variability, on the other hand, is lower in the cold state and higher for the warmer scenarios. There are regions that display opposite patterns: in both hemispheres, precipitation changes at the midlatitude western coasts of the continents (California, Patagonia, South Africa, southern Australia, and the Mediterranean) are the inverse of the global mean change in precipitation. They display more precipitation variability in the lgm scenario and consistently lower precipitation and precipitation variability in the 1pctCO2 and abrupt4xCO2 scenarios. The circulation modes that affect these regions remain consistent across the model ensemble. We investigated, but did not find, a universal relationship between the variability of climate modes and global mean temperature change. No model shows a reduction in temperature variance as large as that for the centennial to millennial timescales observed in paleoclimate data for the last glacial to Holocene transition, but this could be due to the much shorter timescales we have investigated here. Yet, on seasonal to multidecadal timescales, we find evidence of scaling and that changes in variability appear to occur proportionally across these timescales. Interannual precipitation variability across these simulations appears to robustly and linearly relate the relative change in regional variance to the relative change in the mean precipitation. This relationship, and the consistency across timescales, could imply that hydroclimate proxy reconstructions at decadal to centennial timescales provide an additional constraint on simulated past and future precipitation variability changes.