The multi-scale structure of atmospheric energetic constraints on globally averaged precipitation

This study presents a multi-scale analysis of cross-correlations based on Haar fluctuations of globally averaged anomalies of precipitation (P), precipitable water vapor (PWV), surface temperature (T), and atmospheric radiative fluxes. The results revealed an emergent transition between weak correlations at sub-yearly timescales (down to ∼5 days) to strong correlations at timescales larger than about ∼1–2 years (up to ∼1 decade). At multiyear timescales, (i) Clausius–Clapeyron becomes the dominant control of PWV (${\mathit{\rho }}_{\mathrm{PWV},T}\approx \mathrm{0.9}$), (ii) surface temperature averaged over global land and over global ocean (sea surface temperature, SST) become strongly correlated (${\mathit{\rho }}_{\mathrm{Tland},\mathrm{SST}}\sim \mathrm{0.6}$); (iii) globally averaged precipitation variability is dominated by energetic constraints, specifically the surface downwelling longwave radiative flux (DLR) (${\mathit{\rho }}_{\mathrm{P},\mathrm{DLR}}\approx -\mathrm{0.8}$) displayed stronger correlations than the direct response to T fluctuations, and (iv) cloud effects are negligible for the energetic constraints in (iii), which are dominated by clear-sky DLR. At sub-yearly timescales, all correlations underlying these four results decrease abruptly towards negligible values. Such a transition has important implications for understanding and quantifying the climate sensitivity of the global hydrological cycle. The validity of the derived correlation structure is demonstrated by reconstructing global precipitation time series at 2-year resolution, relying on the emergent strong correlations (P vs. clear-sky DLR). Such a simple linear sensitivity model was able to reproduce observed P anomaly time series with similar accuracy to an (uncoupled) atmospheric model (ERA-20CM) and two climate reanalysis (ERA-20C and 20CR). The linear sensitivity breaks down at sub-yearly timescales, whereby the underlying correlations become negligible. Finally, the relevance of the multi-scale framework and its potential for stochastic downscaling applications are demonstrated by deriving accurate monthly P probability density functions (PDFs) from the reconstructed 2-year P time series based on scale-invariant arguments alone. The derived monthly PDFs outperform the statistics simulated by ERA-20C, 20CR, and ERA-20CM in reproducing observations.

1 Introduction

The precipitation response to changes in increased concentrations of greenhouse gases is a central topic for the climate science community. Although its regional variability is essential to determining societal impacts, globally averaged precipitation is an important first-order climate indicator, and a measure of the global water cycle, that must be accurately simulated if robust climate projections are to be obtained across a wide range of spatial and temporal scales.

However, even the long-term response of globally averaged precipitation is still poorly understood, constrained, and simulated (Collins et al., 2013; Allan et al., 2014; Hegerl et al., 2015), largely due to limited knowledge on the complex interactions between the key components of the atmospheric branch of the water cycle and its forcing mechanisms. This problem is tackled here by employing a multi-scale analysis framework to study globally averaged precipitation variability and its relation to two key governing mechanisms: the Clausius–Clapeyron relationship and the constraints imposed by the atmospheric energy balance.

The Clausius–Clapeyron relationship is a well-known mechanism controlling the variability of the global water cycle. Assuming constant relative humidity, it implies that fractional changes in globally averaged precipitable water vapor (ΔPWV ∕ PWV) are linearly related to fluctuations of globally averaged near-surface air temperature (ΔT) (e.g., Held and Soden, 2006; Schneider et al., 2010):

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle \frac{\mathrm{\Delta }\mathrm{PWV}}{\mathrm{PWV}}}\approx {\mathit{\alpha }}_{\mathrm{PWV},T}\mathrm{\Delta }T,\end{array}$$

where ${\mathit{\alpha }}_{\mathrm{PWV},T}\approx \mathrm{0.07}$ K⁻¹ at temperatures typical of the lower troposphere. Numerous studies have provided a robust confirmation for the Clausius–Clapeyron mechanism at multi-decadal to centennial timescales, while also reporting an analogous linear response of globally averaged precipitation to surface temperature fluctuations (see, e.g., Schneider et al., 2010; Trenberth, 2011; O'Gorman et al., 2012; and Allan et al., 2014 for reviews). In general, these previous investigations agree on the ∼7 % K⁻¹ sensitivity coefficient for precipitable water vapor. However, there is large spread of the global precipitation sensitivity coefficient estimates, typically in the 1 % K⁻¹ to 3 % K⁻¹ range.

A widely recognized explanation for the sub-Clausius–Clapeyron sensitivity of precipitation to temperature fluctuations at long temporal scales comes from the atmospheric energy balance (Allen and Ingram, 2002; Stephens and Ellis, 2008; Stephens and Hu, 2010). Specifically, averaging over the global atmosphere, the latent heat flux associated with precipitation formation (L_VP, with P being the globally averaged precipitation flux and L_V the latent heat of vaporization) should be in balance with the net atmospheric radiative flux (R_atm) and the surface sensible flux (F_SH):

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle }{L}_{\mathrm{V}}P+R_{\mathrm{atm}}+F_{\mathrm{SH}}\approx \mathrm{0}.\end{array}$$

Equation (2) represents a general state of radiative convective equilibrium (Pauluis and Held, 2002), with energy fluxes defined as positive for atmospheric gain and negative otherwise.

If the Clausius–Clapeyron relationship was the dominant mechanism controlling the response of atmospheric moisture content and the global water cycle to temperature fluctuations, then globally averaged precipitable water vapor and precipitation could be expected to be strongly correlated with surface temperature. Previously, Gu and Adler (2011, 2012) found strong correlations between the interannual variability of globally averaged precipitable water vapor and surface temperature, in tight agreement with the Clausius–Clapeyron mechanism. However, they found weaker (yet significant) correlations between the interannual variability of globally averaged precipitation and surface temperature, raising doubts regarding whether the Clausius–Clapeyron mechanism could be directly extendable to global precipitation. Note, however, that these results focusing on a single temporal scale might not represent the entire picture.

A further source of complexity comes from the fact that precipitation and other relevant atmospheric variables (including temperature, atmospheric moisture, wind, etc.) display a complex statistical structure, with significant variability over a wide range of temporal scales and with the possibility of different mechanisms governing variability at different timescales (see, e.g., Lovejoy and Schertzer, 2013 for a comprehensive review). Furthermore, it has been shown that this complex multi-scale structure plays a role (at least) as important as the large amplitude periodic components, namely diurnal and seasonal cycles (Lovejoy, 2015; Nogueira, 2017a). However, our understanding of the underlying governing mechanisms at different timescales remains largely elusive, representing a central problem for future improvements to climate simulation and projection.

Recently, Nogueira (2019) analyzed satellite-based observational datasets, a long global climate model (GCM) simulation, and reanalysis products and found a tight correlation (∼0.8) between anomaly (deseasonalized) time series of globally averaged precipitable water vapor and surface temperature, which emerged at timescales larger than ∼1–2 years. In contrast, at smaller timescales the correlation decreased rapidly towards negligible values (<0.3). In other words, the Clausius–Clapeyron relationship is the dominant mechanism of atmospheric moisture anomalies at multiyear timescales, but not at sub-yearly timescales. Nogueira (2019) also found that the magnitude of the correlations between anomaly time series for globally averaged precipitation and surface temperature was negligible at sub-yearly timescales, while at multiyear timescales the results showed large spread amongst different datasets, ranging between negligible (<0.3) and strong (∼0.8) correlation values. Building on this previous study, here the multi-scale analysis of the mechanisms governing global precipitation variability was extended, including the energetic constraints on precipitation represented in Eq. (2). The paper is organized as follows: Sect. 2 describes the considered datasets and the multi-scale analysis framework; the results of multi-scale correlation analysis of precipitation variability are presented and discussed in Sect. 3; and in Sect. 4 the validity of the linear sensitivity correlations derived from the multi-scale analysis is demonstrated by employing a simple linear model to reconstruct globally averaged precipitation time series from energetic constraints. At sub-yearly timescales, at which the correlations break down, it is shown in Sect. 5 how the monthly statistics can be reproduced by employing a stochastic downscaling algorithm based on scale-invariant symmetries of precipitation. Finally, the main conclusions are summarized and discussed in Sect. 6.

2 Data and methodology

2.1 Datasets

Precipitation observations were obtained from the Global Precipitation Climatology Project (GPCP) version 2.3 monthly precipitation dataset (Adler et al., 2003), which covers the full globe at 2.5^∘ resolution from 1979 to present. Gridded datasets of monthly average surface temperatures were obtained from the Goddard Institute for Space Studies (GISSTEMP) analysis (Hansen et al., 2010), which covers the globe at 2^∘ resolution from 1880 to present, with the values provided as anomalies relative to the 1951–1980 reference period. GISSTEMP blends near-surface air temperature measurements from meteorological stations (including Antarctic stations) with a reconstructed sea surface temperature (SST) dataset over oceans. Observations of atmospheric radiative fluxes were obtained from the National Aeronautics and Space Administration (NASA) Clouds and the Earth's Radiant Energy System, Energy Balanced and Filled (CERES-EBAF) edition 4.0 (Loeb et al., 2009), a monthly dataset covering the full globe at 1^∘ resolution from March 2000 to June 2017.

Two state-of-the-art reanalyses of the twentieth century were considered in the present study. One was the National Oceanic and Atmospheric Administration Cooperative institute for Research in Environmental Sciences (NOAA-CIRES) twentieth-century reanalysis (20CR) version 2c (Compo et al., 2011), which covers the full globe at 2^∘ resolution, spanning from 1851 to 2014. Only surface pressure observations and reports are assimilated in this reanalysis. SST boundary conditions are obtained from 18 members of Simple Ocean Data Assimilation with Sparse Input (SODAsi) version 2, with the high latitudes corrected to the Centennial in Situ Observation-Based Estimates of the Variability of SST and Marine Meteorological Variables version 2 (COBE-SST2). Here, global-mean time series of precipitation, precipitable water vapor, near-surface temperature, SST, and atmospheric radiative fluxes were obtained from 20CR at daily resolution for the 1900–2010 period. Note that the net atmospheric radiative flux cannot be obtained from 20CR because the incoming solar radiation at the top of the atmosphere is not available for this dataset due to an error with output processing.

The other reanalysis considered in the present study was the European Centre for Medium-Range Weather Forecasts (ECMWF) twentieth-century reanalysis (ERA-20C; Poli et al., 2015), which covers the full globe at 1^∘ resolution spanning 1900–2010. It assimilates marine surface winds from the International Comprehensive Ocean–Atmosphere Data Set version 2.5.1 (ICOADSv2.5.1) and surface and mean sea-level pressure from the International Surface Pressure Databank version 3.2.6 (ISPDv3.2.6) and from ICOADSv2.5.1. SST boundary conditions are obtained from the Hadley Centre Sea Ice and Sea Surface Temperature dataset version 2.1 (HadISST2.1). Global-mean time series of precipitation, precipitable water vapor, near-surface temperature, SST, and atmospheric radiative fluxes were obtained from ERA-20C at daily resolution for the 1900–2010 period.

Finally, the uncoupled ECMWF twentieth-century ensemble of 10 atmospheric model integrations (ERA-20CM; Hersbach et al., 2015) was considered, which uses the same model, grid, initial conditions, and radiative and aerosol forcings as ERA-20C. However, no observations are assimilated, the simulation is integrated continuously over the full 1900–2010 period, and SST is prescribed by an ensemble of realizations from HadISST2.1, including one control simulation and nine simulations with perturbed SST and sea ice concentration. A 10-member ensemble of global-mean time series of precipitation, precipitable water vapor, near-surface temperature, SST, and atmospheric radiative fluxes was obtained from ERA-20CM at monthly resolution for the 1900–2010 period. Considering ERA-20CM allowed for the testing of the sensitivity of the multi-scale correlation structure derived from ERA-20C to data assimilation, but different atmospheric evolutions associated with perturbations to the forcing fields (particularly to SST).

Note that the clear-sky radiative fluxes considered here obtained from ECMWF datasets are computed for the same atmospheric conditions of temperature, humidity, ozone, trace gases, and aerosol, but assuming that the clouds are not there. Clear-sky estimates from ERA-20C and ERA-20CM cover the full globe area and not just the cloud-free regions at each time instant. However, they are available for net radiative fluxes, but not for downwelling or upwelling radiation fluxes.

2.2 Multi-scale correlation analysis

Consider two time series, y and y^′, with N data points each. Here the goal is to study the correlation between the fluctuations Δy(Δt) and Δy(Δt) at different timescales Δt. Due to the strong yearly cycle present in the considered time series, the periodic seasonal trend was first eliminated by subtracting the long-term average (over all the years in the record) of each calendar day (or month, depending on temporal resolution):

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle }{y}_{\mathrm{ds}}\left(i\right)=y\left(i\right)-\langle y{\rangle }_{\mathrm{d}},\end{array}$$

where y_ds is the deseasonalized anomalies time series.

Traditionally, fluctuations are defined by the difference $\mathrm{\Delta }y\left(\mathrm{\Delta }t\right)=y(t+\mathrm{\Delta }t)-y\left(t\right)$. However, it has been shown that such definition is only appropriate for fluctuations increasing with timescale (Lovejoy and Schertzer, 2013). Consequently, the traditional a definition is not useful for the present study, since the fluctuations for most atmospheric variable time series (including temperature, rain, wind, and water vapor, amongst others) decrease with increasing timescale over the tens of days to tens of years range (e.g., Lovejoy and Schertzer, 2013; Lovejoy, 2015; Lovejoy et al., 2017; Nogueira, 2017a, b, 2019). In this sense, here the fluctuations were defined using the Haar wavelet, which is appropriate for the full range of timescales and all atmospheric variables considered, in cases in which fluctuations both increase and decrease with timescale. Furthermore, correlations computed from Haar fluctuation time series also avoid the low-frequency biases that emerge in standard correlation analysis due to climate variability (see Lovejoy et al., 2017, for a detailed description of the Haar fluctuations and correlations of Haar fluctuations).

The Haar fluctuations are simply defined as the difference of the means from $t+\mathrm{\Delta }t/\mathrm{2}$ to $t+\mathrm{\Delta }t/\mathrm{2}$ and from t to $t+\mathrm{\Delta }t/\mathrm{2}$, i.e.,

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle }\left(\mathrm{\Delta }y\right(\mathrm{\Delta }t){)}_{\mathrm{Haar}}={\displaystyle \frac{\mathrm{2}}{\mathrm{\Delta }t}}\underset{t+\mathrm{\Delta }t/\mathrm{2}}{\overset{t+\mathrm{\Delta }t}{\int }}y(t)\mathrm{d}t-{\displaystyle \frac{\mathrm{2}}{\mathrm{\Delta }t}}\underset{t}{\overset{t+\mathrm{\Delta }t/\mathrm{2}}{\int }}y(t)\mathrm{d}t.\end{array}$$

For the sake of simplicity, henceforth the fluctuation notation Δy(Δt) will be employed to refer to Haar fluctuations (i.e., Δy(Δt)≡(Δy(Δt))_Haar). A Haar fluctuation time series was computed by employing Eq. (4) at each instant of the deseasonalized anomaly time series for each variable considered. Finally, at each timescale, Δt, the correlation coefficient, ρ, of the corresponding Haar fluctuations time series was computed for each pair of variables considered.

Note that, in computing correlations at timescales larger than 2 times the original time series resolution, there is overlap of the data points considered in computing the Haar fluctuations. While this could introduce spurious effects in the computed correlations, previous works have shown the robustness of the Haar-fluctuation-based correlation methodology used here (e.g., Lovejoy et al., 2017). Additionally, the analogous method of detrended cross-correlation analysis has also been employed on overlapping windows and demonstrated to provide accurate correlation estimates at different timescales using overlapping windows (see, e.g., Podobnik and Stanley, 2008; Podobnik et al., 2011; Piao and Fu, 2016). In fact, in Sect. 3 below it is shown that identical correlation structures are obtained between correlations of Haar fluctuations and detrended cross-correlation analysis. Since the multi-scale cross-correlation structure obtained with Haar fluctuations is identical to the results using detrended cross-correlation analysis, it is assumed that critical points for the 95 % significance level of Haar fluctuation correlations are identical to the ones demonstrated by Podobnik et al. (2011) for detrended cross-correlation analysis using overlapping windows, whereby the significant values can vary between values below 0.1 and up to about 0.4, depending on the time series length, the considered timescale, and the power-law exponents of both time series. In this sense, here it is assumed that correlation magnitudes below 0.3 are nonsignificant and that magnitudes in the 0.3 to 0.4 range should be interpreted with care.

3 Analysis of the mechanisms governing P variability across timescales

3.1 Multi-scale structure of the atmospheric water cycle response to surface temperature fluctuations

The correlations between Haar fluctuation time series revealed strong correlations (∼0.9) between deseasonalized anomaly time series for globally averaged precipitable water vapor and near-surface temperature (or, alternatively, SST) at multiyear timescales (Fig. 1a). However, as the timescale decreases there is a transition in the correlation structure, and negligible correlations (<0.3) emerge at sub-yearly timescales. This result suggested that the Clausius–Clapeyron relationship (see Eq. 1) holds to a very good approximation at multiyear timescales, but not at sub-yearly timescales. Interestingly, Lovejoy et al. (2017) computed the Haar fluctuation correlations for GISSTEMP surface temperatures and found a similar transition in the multi-scale correlation structure of SST against globally averaged surface temperature, with low correlations at timescales below a few months and strong correlations (∼0.8) at multiyear timescales. Note that the latter strong correlations were not surprising, since SST was a major component in their definition of globally averaged surface temperature (which for GISSTEMP uses SST over ocean pixels and 2 m air temperature over land pixels). Nonetheless, Lovejoy et al. (2017) also found a similar transition for the correlation between SST and near-surface air temperature averaged over global land, with maximum correlation values ∼0.6 at multiyear timescales. The transition in the correlation structure between SST and global land temperature was confirmed here for ERA-20C, ERA-20CM, 20CR, and GISSTEMP (Fig. 1b). Thus, the present results support the Lovejoy et al. (2017) argument that these abrupt correlation changes correspond to a fundamental behavioral transition, whereby the atmosphere and the oceans start to act as a single coupled system. Furthermore, the results presented here suggest that precipitable water vapor anomalies at multiyear resolution can be derived, to a very good approximation, from SST alone.

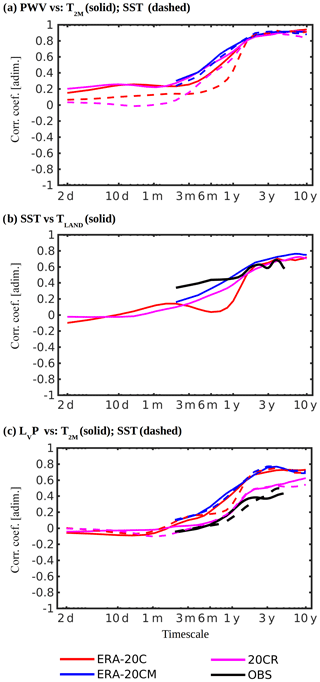
Figure 1 Cross-correlation coefficients against temporal scale computed from Haar fluctuations for global-mean time series of (a) PWV vs. T_2 m (solid) and PWV vs. SST (dashed); (b) SST vs. T_land; and (c) L_vP vs. T_2 m (solid) and L_vP vs. SST (dashed). Red lines represent results from ERA-20C, blue lines are from ERA-20CM, pink lines are from 20CR, and black lines are estimated from observational products.

Nogueira (2019) also reported a transition in the multi-scale correlation structure between deseasonalized anomaly time series of globally averaged precipitation and surface temperature (considering SST over the oceans and 2 m air temperature over land), with negligible values at sub-yearly timescales, but with large spread in the magnitude of the multiyear correlations ranging between ∼0.3 and ∼0.8. Here, a similar result was found for the multi-scale correlation structure between globally averaged precipitation and surface temperature and also globally averaged precipitation and SST (Fig. 1c), with large spread in correlation magnitude at multiyear timescales (∼0.7 in ERA-20C and ERA-20CM, ∼0.6 in 20CR, and ∼0.4 in observations). Furthermore, considering different time lags in computing the cross-correlations between precipitation and surface temperature did not reveal the presence of significant lagged correlations over the daily to decadal timescale range.

3.2 Multi-scale structure of the energetic constraints to precipitation variability

A study of the circulation component of the precipitation response to temperature fluctuations requires a detailed representation of several spatially heterogeneous variables and their nonlinear interactions. An alternative path towards understanding globally averaged precipitation temporal variability was taken in the present investigation, focusing on the constraints imposed by the atmospheric energy balance represented in Eq. (2). Figure 2a (solid lines) shows that the estimated multi-scale correlation coefficients between the deseasonalized anomaly time series for precipitation and net atmospheric radiative fluxes were strongly (negatively) correlated at multiyear timescales ($\left|\mathit{\rho }\right|=\mathrm{0.8}$ in ERA-20C, ERA-20CM, and observations), in agreement with the balance in Eq. (2). In contrast, at sub-yearly timescales the correlation magnitude decreased rapidly, changed sign around monthly timescales, and reached values ∼0.4 at timescales below about 10 days.

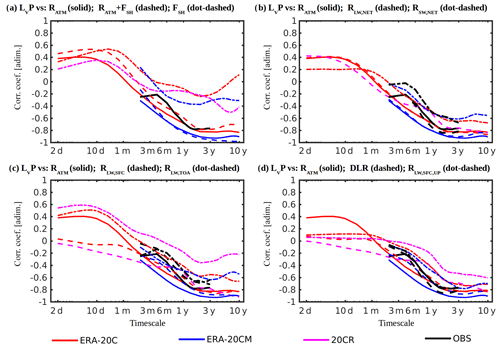
Figure 2 Cross-correlation coefficients against temporal scale computed from Haar fluctuations of (a) L_vP vs. R_atm (solid), L_vP vs. (R_atm+F_SH) (dashed), and L_vP vs. F_SH (dot-dashed); (b) L_vP vs. R_atm (solid), L_vP vs. R_LW,net (dashed), and L_vP vs. R_SW,net (dot-dashed); (c) L_vP vs. R_atm (solid), L_vP vs. R_LW,SFC (dashed), and L_vP vs. R_LW,TOA (dot-dashed); and (d) L_vP vs. R_atm (solid), L_vP vs. DLR (dashed), and L_vP vs. $R_{\mathrm{LW},\mathrm{SFC},\mathrm{UP}}$ (dot-dashed). Red lines are computed from ERA-20C, blue lines are from ERA-20CM, pink lines are from 20CR, and black lines are computed from GPCP and CERES-EBAF observational products. Note that R_atm and R_SW,net were not available from 20CR, while sensible heat flux was not available from observations.

Considering the combined effect of the net atmospheric radiative fluxes and sensible heat flux in Eq. (2) slightly increased the (positive) correlations at sub-monthly timescales (Fig. 2a, dashed lines), although the absolute changes are essentially below 0.1. More importantly, Fig. 2a shows that the magnitude of the correlation at multiyear timescales between globally averaged precipitation and net atmospheric radiative fluxes is significantly larger than when the combined effect of net atmospheric radiative fluxes and sensible heat flux was considered. Indeed, the correlation between globally averaged precipitation and sensible heat flux displayed values up to about 0.5 at sub-monthly timescales, but essentially <0.4 at multiyear timescales (Fig. 2a, dot-dashed lines). Given the results in Fig. 2a, the following linear relation was hypothesized: $L_{\mathrm{V}}\mathrm{\Delta }P\approx c_{\mathrm{1}}\times (-\mathrm{\Delta }{R}_{\mathrm{atm}})+c_{\mathrm{2}}$, where c₁ and c₂ are arbitrary constants, and Δ represents fluctuations taken as deseasonalized anomalies at multiyear resolutions. At sub-yearly timescales this simplification is not adequate, since the correlations between globally averaged precipitation and net atmospheric radiative fluxes become negligible. In other words, the energy balance represented in Eq. (2) does not represent the dominant constraint on precipitation variability at sub-yearly timescales, most likely due to non-negligible changes in atmospheric heat storage.

The analysis was extended by decomposing the net atmospheric radiative flux into its net atmospheric longwave and shortwave radiative flux components, i.e., $R_{\mathrm{atm}}=R_{\mathrm{LW},\mathrm{net}}+R_{\mathrm{SW},\mathrm{net}}$. On the one hand, the correlation between globally averaged precipitation and net atmospheric radiative fluxes is nearly identical to the correlation between globally averaged precipitation and net atmospheric longwave radiative fluxes (i.e., ${\mathit{\rho }}_{\mathrm{P},{\mathrm{R}}_{\mathrm{atm}}}\approx {\mathit{\rho }}_{\mathrm{P},{\mathrm{R}}_{\mathrm{LW},\mathrm{net}}}$) over the full range of timescales considered (Fig. 2b). On the other hand, ${\mathit{\rho }}_{\mathrm{P},{\mathrm{R}}_{\mathrm{SW},\mathrm{net}}}$ also displayed significant values (∼0.6) at multiyear timescales, but the latter magnitude was nearly 0.2 lower when compared to ${\mathit{\rho }}_{\mathrm{P},{\mathrm{R}}_{\mathrm{atm}}}$ and ${\mathit{\rho }}_{\mathrm{P},{\mathrm{R}}_{\mathrm{LW},\mathrm{net}}}$ (Fig. 2b). Consequently, the above linear relationship for multi-scale P anomalies was further refined as $L_{\mathrm{V}}\mathrm{\Delta }P\approx c_{\mathrm{1}}\times (-\mathrm{\Delta }{R}_{\mathrm{atm}})+c_{\mathrm{2}}\approx c_{\mathrm{3}}\times (-\mathrm{\Delta }{R}_{\mathrm{LW},\mathrm{net}})+c_{\mathrm{4}}$, where c₃ and c₄ are arbitrary constants.

Subsequently, the net atmospheric longwave radiative flux was further decomposed into the top-of-atmosphere (TOA) and surface net longwave fluxes, i.e., $R_{\mathrm{LW},\mathrm{net}}=R_{\mathrm{LW},\mathrm{TOA}}+R_{\mathrm{LW},\mathrm{SFC}}$. At multiyear timescales, ${\mathit{\rho }}_{\mathrm{P},{\mathrm{R}}_{\mathrm{atm}}}\approx {\mathit{\rho }}_{\mathrm{P},{\mathrm{R}}_{\mathrm{LW},\mathrm{SFC}}}$ (Fig. 2c), suggesting that the surface net longwave radiative fluxes provide the main constraint to globally averaged precipitation variability. The correlation between globally averaged precipitation and TOA longwave radiative fluxes also displayed significant values at multiyear timescales, up to $\sim -\mathrm{0.6}$ in ERA-20C and ERA-20CM datasets, but much lower in 20CR in which the magnitude of the correlation was <0.4 at multiyear timescales. Nonetheless, the former correlations (in ERA-20C and ERA-20CM) were in better agreement with observations, suggesting that significant (negative) correlations existed between globally averaged precipitation and net longwave fluxes for TOA anomalies at multiyear timescales. However, for all datasets, the magnitude of ${\mathit{\rho }}_{\mathrm{P},{\mathrm{R}}_{\mathrm{LW},\mathrm{TOA}}}$ at multiyear timescales was nearly 0.2 lower than for ${\mathit{\rho }}_{\mathrm{P},{\mathrm{R}}_{\mathrm{LW},\mathrm{SFC}}}$. Consequently, a further approximation was considered on the linear model for precipitation fluctuations at multiyear timescales: $L_{\mathrm{V}}\mathrm{\Delta }P\approx c_{\mathrm{1}}\times (-\mathrm{\Delta }{R}_{\mathrm{atm}})+c_{\mathrm{2}}\approx c_{\mathrm{3}}\times (-\mathrm{\Delta }{R}_{\mathrm{LW},\mathrm{net}})+c_{\mathrm{4}}\approx c_{\mathrm{5}}\times (-\mathrm{\Delta }{R}_{\mathrm{LW},\mathrm{SFC}})+c_{\mathrm{6}}$.

Finally, the surface net longwave radiative flux can be further decomposed into its upwelling and downwelling (henceforth denoted downwelling longwave radiation, DLR) components. Figure 2d shows that, at multiyear timescales, the differences in the correlations of globally averaged precipitation against DLR (ρ_P,DLR) or against net atmospheric radiative fluxes (i.e., ${\mathit{\rho }}_{\mathrm{P},{\mathrm{R}}_{\mathrm{atm}}}$) were within 0.1 in observations, ERA-20C, and ERA-20CM (R_atm is unavailable for 20CR). Thus, at multiyear timescales, the fluctuations in downwelling surface longwave radiative fluxes are, to a good approximation, linearly related to precipitation fluctuations: $L_{\mathrm{V}}\mathrm{\Delta }P\approx c_{\mathrm{7}}\times (-\mathrm{\Delta }\mathrm{DLR})+c_{\mathrm{8}}$. Note that the correlation structure of globally averaged precipitation against upwelling surface radiative fluxes or against net atmospheric radiative fluxes is nearly identical in observations. However, significant differences emerged between these two quantities (∼0.2) in ERA-20CM and ERA-20C. Thus, a similar linear relationship between ΔP and $\mathrm{\Delta }{R}_{\mathrm{LW},\mathrm{SFC},\mathrm{UP}}$ might also hold to a good approximation, although the results are less robust than for ΔP against ΔDLR.

The correlation between globally averaged precipitation and clear-sky net radiative atmospheric heating (i.e., ${\mathit{\rho }}_{\mathrm{P},{\mathrm{R}}_{\mathrm{atm},\mathrm{cs}}}$) was nearly identical to ${\mathit{\rho }}_{\mathrm{P},{\mathrm{R}}_{\mathrm{atm}}}$ at multiyear timescales (Fig. 3a). This suggested that the cloud effects on the multiyear linear dependence between precipitation variability and net atmospheric radiative fluxes may be neglected. But the same is not true at timescales below a few months, at which significant differences emerge between ${\mathit{\rho }}_{\mathrm{P},{\mathrm{R}}_{\mathrm{atm},\mathrm{cs}}}$ and ${\mathit{\rho }}_{\mathrm{P},{\mathrm{R}}_{\mathrm{atm}}}$. The clear-sky approximation holds at multiyear timescales for correlations of globally averaged precipitation against net atmospheric longwave radiative fluxes and also against the globally averaged net surface longwave fluxes (Fig. 3b). Based on these results, it was further hypothesized that cloud effects are also negligible for the correlation between globally averaged precipitation and DLR at multiyear temporal scales. This hypothesis could not be tested directly because clear-sky DLR time series were not available for the ECMWF datasets. Nonetheless, the results in Sect. 4 based on an empirical algorithm for DLR estimation under a clear-sky approximation provided support for this hypothesis.

Figure 3 Cross-correlation coefficients against temporal scale computed from Haar fluctuations of (a) L_vP vs. R_atm (solid) and L_vP vs. R_atm,CS (dashed); (b) L_vP vs. R_LW,SFC (solid) and L_vP vs. $R_{\mathrm{LW},\mathrm{SFC},\mathrm{CS}}$ (dashed). Red lines are computed from ERA-20C and blue lines are from ERA-20CM.

At this point, it is important to note that the existence of strong correlations does not necessarily imply causality between two variables. However, the atmospheric energy balance in Eq. (2) provides a physical basis for the obtained strong (negative) correlation values between precipitation and atmospheric radiative fluxes. In fact, the multi-scale analysis presented here provided further robustness to previous investigations on the importance of energetic constraints to global precipitation, the dominant role of surface longwave fluxes, namely DLR, and the negligible cloud effects in these relationships (e.g., Stephens and Hu, 2010; Stephens et al., 2012a, b). More importantly, a clear transition emerged between robust correlations at multiyear timescales and negligible correlations at sub-yearly timescales, which was found for globally averaged precipitation against atmospheric radiative fluxes (particularly total net, net longwave, and DLR), globally averaged precipitable water vapor against surface temperature (and SST), global SST against global near-surface air temperature, and, less robustly, globally averaged precipitation against surface temperature (or SST).

Note that the correlation structure derived from Haar fluctuations of different combinations of variables presented in the present section is identical to the correlation structure obtained by employing detrended cross-correlation analysis (DCCA; see Figs. S1–S3 in the Supplement). DCCA has been previously shown to robustly quantify correlations at different timescales (Podobnik and Stanley, 2008; Piao and Fu, 2016; Nogueira, 2017b, 2019, where detailed descriptions of DCCA methodology are also provided). This result provides one of the first empirical verifications for the multi-scale correlation obtained from Haar fluctuations recently introduced by Lovejoy et al. (2017).

4 Evaluation of the multiyear linear relationships between globally averaged precipitation, clear-sky DLR, and surface temperature

The strong correlations between globally averaged precipitation and atmospheric longwave radiative fluxes imply that a simple linear model should be able to reproduce the variability in precipitation anomalies at multiyear timescales. This hypothesis is tested in the present section, aiming to provide robustness to the strong multiyear correlations presented in Sect. 3. Specifically, the robustness of the tight correlation between globally averaged precipitation and clear-sky DLR at multiyear timescales is tested. Additionally, whether the more robust correlation between globally averaged precipitation and clear-sky DLR at multiyear timescales compared to globally averaged precipitation against surface temperature results in a better reconstruction of precipitation variability by such a linear model is tested.

The clear-sky DLR can be derived, to a good approximation, from the globally averaged near-surface temperature alone (e.g., Stephens et al., 2012b). Furthermore, given the tight coupling between globally averaged temperature over land and SST at multiyear timescales (Fig. 1b), it is hypothesized that clear-sky DLR variability could be obtained, to a good approximation, directly from the SST forcing. This hypothesis is also supported by the nearly identical correlations between globally averaged precipitable water vapor against surface temperature or against SST (Fig. 1a).

Here two different algorithms to estimate clear-sky DLR are tested: the Dilley–O'Brien model (Dilley and O'Brien, 1998) and the Prata model (Prata, 1996). In the Dilley–O'Brien model,

$$\begin{array}{ll}{\displaystyle }{\mathrm{DLR}}_{\mathrm{2}\mathrm{y},\mathrm{DO}}& {\displaystyle }=a_{\mathrm{1}}+a_{\mathrm{2}}{\left({\displaystyle \frac{{\mathrm{SST}}_{\mathrm{2}\mathrm{y}}}{{\mathrm{SST}}_{\mathrm{c}}}}\right)}^{\mathrm{6}}\\ \text{(5)}& {\displaystyle }& {\displaystyle }+a_{\mathrm{3}}{\left({\displaystyle \frac{\mathrm{\Delta }{\mathrm{PWV}}_{\mathrm{2}\mathrm{y}}+{\mathrm{PWV}}_{\mathrm{c}}}{{\mathrm{PWV}}_{\mathrm{c}}}}\right)}^{\mathrm{1}/\mathrm{2}},\end{array}$$

where a₁=59.38 W m⁻², a₂=113.7 W m⁻², and a₃=96.96 W m⁻² are the model parameters, and PWV_c=22.5 kg m⁻² is the climatological value for precipitable water vapor. The subscript “2 y” (e.g., DLR_2 y) indicates a fluctuation for Δt=2 years. Note that DLR${}_{\mathrm{c},\mathrm{DO}}=a_{\mathrm{1}}+a_{\mathrm{2}}+a_{\mathrm{3}}$ is obtained by replacing the climatological values of PWV and SST in Eq. (8).

The Prata model for ΔDLR_2 y,Pr is based on the Stefan–Boltzmann equation:

$$\begin{array}{}\text{(6)}& {\displaystyle }{\displaystyle }{\mathrm{DLR}}_{\mathrm{2}\mathrm{y},\mathrm{Pr}}={\mathit{\epsilon }}_{\mathrm{clr}}{\mathit{\sigma }}_{\mathrm{SB}}{\mathrm{SST}}_{\mathrm{2}\mathrm{y}}^{\mathrm{4}},\end{array}$$

where ${\mathit{\sigma }}_{\mathrm{SB}}=\mathrm{5.67}\times {\mathrm{10}}^{-\mathrm{8}}$ W m⁻² K⁻⁴ is the Stefan–Boltzmann constant and

$$\begin{array}{}\text{(7)}& {\displaystyle }{\displaystyle }{\mathit{\epsilon }}_{\mathrm{clr}}=\mathrm{1}-\left(\mathrm{1}+{\mathrm{PWV}}_{\mathrm{2}\mathrm{y}}\right)\exp \left(-{\left(\mathrm{1.2}+\mathrm{3}{\mathrm{PWV}}_{\mathrm{2}\mathrm{y}}\right)}^{\mathrm{1}/\mathrm{2}}\right).\end{array}$$

The anomaly time series is computed from ΔDLR${}_{\mathrm{2}\mathrm{y},\mathrm{Pr}}={\mathrm{DLR}}_{\mathrm{2}\mathrm{y},\mathrm{Pr}}-{\mathrm{DLR}}_{\mathrm{c},\mathrm{Pr}}$, where DLR_c,Pr is obtained by replacing the climatological values of PWV and SST in Eqs. (9) and (10).

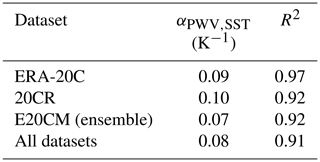
The strong correlation between globally averaged precipitable water vapor and SST at multiyear timescales (Fig. 1a) allowed for the removal of the PWV dependence in Eqs. (8) and (11) by replacing PWV${}_{\mathrm{2}\mathrm{y}}\approx {\mathit{\alpha }}_{\mathrm{PWV},\mathrm{SST}}\mathrm{\Delta }{\mathrm{SST}}_{\mathrm{2}\mathrm{y}}+{\mathrm{PWV}}_{\mathrm{c}}$. The forcing ΔSST_2 y time series were obtained by coarse-graining the deseasonalized (using Eq. 3) globally averaged SST obtained from the GISSTEMP dataset. The sensitivity coefficient, ${\mathit{\alpha }}_{\mathrm{W},\mathrm{SST}}\approx \mathrm{0.08}$ K⁻¹, was estimated by least-squares regression of ΔPWV_2 y∕PWV_c against ΔSST_2 y, pooling together all datasets (ERA-20C, ERA-20CM, and 20CR). The α_PWV,SST estimates are summarized in Table 1, including for each individual dataset, ranging between 0.07 and 0.10 K⁻¹. Note that the obtained values are close to the typical 0.07 K⁻¹ value predicted by the Clausius–Clapeyron relationship.

Table 1 Linear regression coefficient α_W,SST estimated from ΔPWV ∕ PWV_c against ΔSST at 2-year resolution, assuming a relationship as given by Eq. (1). The respective coefficient of determination is also provided. The α_W,SST values are computed for ERA-20C, 20CR, and for the ensemble of ERA-20CM simulations. Additionally, the coefficient is estimated by pooling together ERA-20C, ERA-20CM (ensemble), and 20CR datasets.

In this way, two reconstructed anomaly time series for globally averaged precipitation were obtained using the Dilley–O'Brien and the Prata algorithms. The climatological globally averaged precipitation P_c≈2.7 mm d⁻¹ was estimated from the GPCP dataset. The sensitivity coefficient ${\mathit{\alpha }}_{\mathrm{P},\mathrm{DLR}}\approx \mathrm{0.004}$ (W m²)⁻¹ was estimated by least-squares regression of ΔP_2 y∕P_c against ΔDLR_2 y, pooling together all available datasets (ERA-20C, ERA-20CM, 20CR, and GPCP against CERES-EBAF). Note that, in estimating α_P,DLR, clear-sky DLR time series were used where available (i.e., for ERA-20C and ERA-20CM), but they were replaced by (full-sky) DLR otherwise (i.e., for 20CR and CERES-EBAF). The α_P,DLR estimates are summarized in Table 2, including values obtained from each dataset (no estimate was made for GPCP against CERES-EBAF due to the limited duration of the latter), ranging between 0.003 (W m²)⁻¹ and 0.005 (W m${}^{-\mathrm{2}}{)}^{-\mathrm{1}}$.

Table 2 Linear regression coefficient α_P,DLR estimated from ΔP∕P_c against ΔDLR at 2-year resolution, assuming a relationship as given by Eq. (11). The respective coefficients of determination are also provided. The α_P,DLR values are computed for ERA-20C, 20CR, and for the ensemble of ERA-20CM simulations. Additionally, the coefficient is estimated by pooling together all datasets, including GPCP observations against DLR from CERES-EBAF.

Another simple linear model for the reconstruction of multiyear globally averaged precipitation anomaly time series was tested based on the direct response (correlations) of P to SST fluctuations, i.e., $P_{\mathrm{2}\mathrm{y},\mathrm{SST}}\approx {\mathit{\alpha }}_{\mathrm{P},\mathrm{SST}}\mathrm{\Delta }{\mathrm{SST}}_{\mathrm{2}\mathrm{y}}{P}_{\mathrm{c}}+P_{\mathrm{c}}$. Again, ΔSST_2 y was obtained from the GISSTEMP dataset. The sensitivity coefficient, ${\mathit{\alpha }}_{\mathrm{P},\mathrm{SST}}\approx \mathrm{0.02}$ K⁻¹, was estimated by least-squares regression of ΔP_2 y∕P_c against ΔSST_2 y, pooling together all datasets (ERA-20C, ERA-20CM, 20CR, and GPCP against GISSTEMP). The α_P,SST estimates are summarized in Table 3, including for each individual dataset, ranging between 0.02 and 0.04 K⁻¹. Note that the obtained values are close to the 0.01 to 0.03 K⁻¹ range reported in the relevant literature (e.g., Schneider et al., 2010; Trenberth, 2011; O'Gorman et al., 2012; Allan et al., 2014).

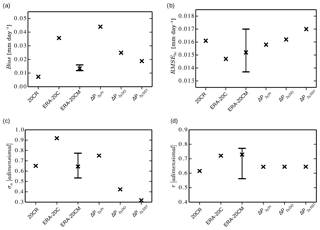
Figure 4 Error estimates from simulated anomaly time series for P at 2-year resolution against GPCP computed for the 1979–2010 period, including (a) mean bias (Bias), (b) root mean square error after bias correction (RMSEbc), (c) model standard deviation normalized by observed standard deviation (σ_n), and (d) Pearson correlation coefficient (r). For the ERA-20CM dataset the range for all ensemble members is shown, while “x” marks their mean value. The p value for all correlations shown in (d) is <0.05.

Table 3 Linear regression coefficient α_P,SST estimated from ΔPP_c against ΔSST at 2-year resolution. The respective coefficients of determination are also provided. The α_P,SST values are computed for ERA-20C, 20CR, for the ensemble of ERA-20CM simulations, and for GPCP against ERA-20CM control SST forcing. Additionally, the coefficient is estimated by pooling together all datasets.

When compared against ΔP_2 y directly derived from GPCP for the 1979 to 2010 period, the errors in the proposed linear ΔP_2 y reconstructions were generally close to those for atmospheric-model-based products (Fig. 4). ΔP_2 y,Pr displays the highest mean bias, somewhat higher than for atmospheric-model-based datasets, but also higher than the mean bias for ΔP_2 y,DO and ΔP_2 y,SST (Fig. 4a). Note that all atmospheric-model-based products considered here also display a positive bias. While this may be due to a negative bias of GPCP (e.g., Gehne et al., 2016), this observational dataset represents the longest reliable dataset for global precipitation studies and was thus considered here as “the truth”. More importantly, the mean bias is easy to correct by simply subtracting its value from the time series. This correction was implemented here for all atmospheric-model-based and linear-model-based ΔP_2 y time series. Figure 4c shows that the normalized standard deviation (${\mathit{\sigma }}_{\mathrm{n}}={\mathit{\sigma }}_{\mathrm{2}\mathrm{y},\mathrm{model}}/{\mathit{\sigma }}_{\mathrm{2}\mathrm{y},\mathrm{obs}}$) estimated from ΔP_2 y,DO (∼0.4) and, particularly, from ΔP_2 y,SST (∼0.3) was lower than the values estimated from atmospheric-model-based products (∼0.5–0.9). In contrast, σ_n estimated from ΔP_2 y,Pr was nearly 0.8, which was higher than 20CR and most members in the ERA-20CM ensemble, and was only outperformed by the ERA-20C dataset. The root mean square error after bias correction (RMSE_bc) estimated from ΔP_2 y,Pr and ΔP_2 y,DO was well within the range of values obtained from atmospheric-model-based products (Fig. 4b), with the Prata model slightly overperforming the Dilley–O'Brien model. RMSE_bc estimated from ΔP_2 y,SST was on the high end of the atmospheric-model-based range of values and somewhat worse than for the DLR-based linear models. Finally, the Pearson correlation coefficient between models and observations (Fig. 4d) was similar amongst all linear-based models and well within the range of values estimated from the atmospheric-model-based products. The latter result was expected since all linear models were forced by the same SST time series.

Overall, these results suggested that ΔP_2 y,Pr (after bias correction) reproduced the observations with similar accuracy to atmospheric-model-based products, including similar RMSE_bc, variability amplitude, and phase of the signal. ΔP_2 y,DO displayed a similar performance for RMSE_bc and for the phase, but not for the variability amplitude. Finally, ΔP_2 y,SST had the worst performance concerning RMSE_bc, but also in capturing the variability amplitude, while it displayed a similar ability as the other linear models in reproducing the phase. The overall weakest performance of ΔP_2 y,SST was coherent with the less robust correlations underlying this model. Additionally, the results indicate that the nonlinear transformations on SST employed in the Prata and the Dilley–O'Brien algorithms improved the linear models.

5 Exploring scale invariance for stochastic downscaling of precipitation to monthly resolution

At sub-yearly timescales, the magnitude of the correlations between globally averaged precipitable water vapor and SST, precipitation and DLR, and precipitation and SST decreases abruptly to negligible values (see Sect. 3). Additionally, the cloud effects on the energetic constraints of precipitation variability become non-negligible (Fig. 3). Consequently, the linear relationships underlying the above simple linear reconstructions of globally averaged precipitation at 2-year resolution are no longer appropriate at sub-yearly timescales. Previous investigations have suggested that this transition should be related to a fundamental transition in the stochastic scale-invariant behavior of climate variables, which separates a high-frequency weather regime that extends up to about the synoptic scales (around 10 days to 1 month in the atmosphere and around 1 year in the oceans) from a low-frequency weather (or macroweather) regime that extends up to a few decades (see, e.g., Lovejoy et al., 2017; Nogueira, 2019). In the weather regime the amplitude of the fluctuations tends to increase with timescale, while in the macroweather regime the amplitude of the fluctuations tends to decrease with increasing timescale, hence implying a convergence toward the “climate normal” at timescales of a few decades (Lovejoy, 2015).

In the present section, it is shown that the multi-scale analysis framework can also be taken advantage of to perform stochastic downscaling from multiyear to monthly resolution. This exercise allows for the demonstration of the relevance of understanding and characterizing the multi-scale structure of atmospheric variables and its remarkable potential for stochastic downscaling applications.

Building on the strong scale-invariant symmetries present in the variability of global and regional precipitation across wide ranges of timescales (e.g., Lovejoy and Schertzer, 2013; Nogueira et al., 2013; Nogueira and Barros, 2014, 2015; Nogueira, 2017a, b, 2019), an algorithm was proposed here to derive the sub-yearly statistics from the multiyear information alone. The physical basis for this algorithm is that while the atmosphere is governed by continuum mechanics and thermodynamics, it simultaneously obeys statistical turbulence cascade laws (e.g., Lovejoy and Schertzer, 2013; Lovejoy et al., 2017).

Conveniently, precipitation (and many other atmospheric variables) is characterized by low spectral slopes β<1, with quasi-Gaussian and quasi-non-intermittent statistics, at timescales between ∼10 days and a few decades (Lovejoy and Schertzer, 2013; de Lima and Lovejoy, 2015; Lovejoy et al., 2015, 2017; Nogueira, 2017b, 2019). Grounded by these scale-invariant properties, fractional Gaussian noise was used here to generate multiple realizations of downscaled ΔP at monthly resolution from each member of each ΔP_2 y time series:

$$\begin{array}{}\text{(8)}& {\displaystyle }{\displaystyle }\mathrm{\Delta }{P}_{\mathrm{1}\mathrm{m}}\left(t\right)={\mathrm{fGn}}_{\mathrm{1}\mathrm{m}}\left(t\right){\displaystyle \frac{\mathrm{\Delta }{P}_{\mathrm{2}\mathrm{y}}\left(t\right)}{{\mathrm{fGn}}_{\mathrm{2}\mathrm{y}}\left(t\right)}},\end{array}$$

where fGn_1 m is a fractional Gaussian noise, which was computed by first generating a random Gaussian noise (g), then taking its Fourier transform ($\stackrel{\mathrm{̃}}{g}$), multiplying by $k^{-\mathit{\beta }/\mathrm{2}}$, and finally taking the inverse transform to obtain fGn_1 m. The mean of fGn_1 m was forced to be equal to the number of data points of ΔP_2 y. Then fGn_2 y was obtained by coarse-graining fGn_1 m using 24-point (i.e., 2 years) length boxes. In this way, ΔP_1 m,DO, ΔP_1 m,Pr, and ΔP_1 m,SST ensembles are respectively generated from the bias-corrected ΔP_2 y,DO, ΔP_2 y,Pr, and ΔP_2 y,SST time series. A total of 100 plausible realizations are generated for each ensemble, corresponding to 100 different realizations of fGn_1 m. Based on recent investigations of P scale invariance properties, a spectral exponent β≈0.3 is assumed (de Lima and Lovejoy, 2015; Nogueira, 2019). In Eq. (11), the 2-year resolution time series were assumed to have a constant value for every month inside each 2-year period.

Note that a resolution limit should exist for the proposed stochastic downscaling algorithm, namely at timescales below ∼10 days when a fundamental transition occurs in the scaling behavior of most atmospheric fields (including globally averaged precipitation; see, e.g., Lovejoy and Schertzer, 2013; Lovejoy, 2015; de Lima and Lovejoy, 2015; Nogueira, 2017a, b, 2019). At faster timescales intermittency becomes non-negligible and the quasi-Gaussian approximation to the statistics is no longer robust.

The proposed downscaling methodology corresponds to treating the sub-yearly frequencies as random “weather noise”, which is characterized, to a good approximation, by scale-invariant behavior with quasi-Gaussian statistics (Vallis, 2009; Lovejoy et al., 2015). A similar downscaling methodology has been previously demonstrated to reproduce the spatial sub-grid-scale variability of topographic height (Bindlish and Barros, 1996), precipitation (Bindlish and Barros, 2000; Rebora et al., 2006; Nogueira et al., 2013; Nogueira and Barros, 2015), and clouds (Nogueira and Barros, 2014).

Figure 5a shows that the PDFs computed from ΔP_1 m,DO, ΔP_1 m,Pr, and ΔP_1 m,SST were in remarkable agreement with PDFs obtained from the GPCP observational dataset for the 1979–2010 period, representing a significant improvement compared to all atmospheric-model-based products. This improved PDF accuracy was quantified using the Perkins skill score, S score (Perkins et al., 2007), defined as:

$$\begin{array}{}\text{(9)}& {\displaystyle }{\displaystyle }S\mathrm{score}=\mathrm{100}\times \sum _{i=\mathrm{1}}^M\min \left[f_{\mathrm{mod}}\left(i\right),f_{\mathrm{obs}}\left(i\right)\right]\end{array}$$

where f_mod(i) and f_obs(i) are respectively the frequency of the modeled and observed P anomaly values in bin i, M is the number of bins used to compute the PDF (here M=15), and min[x, y] is the minimum between the two values. The S score is a measure of similarity between modeled and observed PDFs such that if a model reproduces the observed PDF perfectly then S score = 100 %.

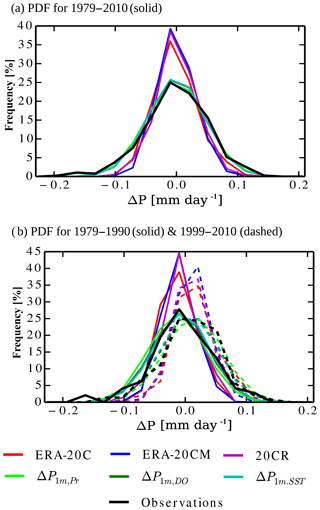
Figure 5 PDFs estimated from monthly anomaly time series for P from ERA-20C (red), ERA-20CM (dark blue), 20CR (pink), GPCP (black), ΔP_1 m,DO (dark green), ΔP_1 m,Pr (light green), and ΔP_1 m,SST (light blue). In (a) the PDFs are estimated for the 1979–2010 period, and in (b) the PDFs are estimated for the 1979–1990 period (solid) and the 1999–2010 period (dashed).

The linear-based models showed S score values around 95 %, which were significantly higher than the ∼80 % found for the atmospheric-model-based products (Fig. 6). Furthermore, the stochastic model captured the change in the PDFs between two separate periods (1979–1990 and 1999–2010; Fig. 5b), while preserving the remarkably high (≥90 %) S scores (Fig. 6, blue and red markers). Indeed, the S scores for linear-based models were consistently better than the S scores obtained from atmospheric-model-based products (∼80 %). Despite some differences between PDFs obtained from ΔP_1 m,DO, ΔP_1 m,Pr, and ΔP_1 m,SST, their similar performance in reproducing observations was somewhat unexpected given the distinct performances in reproducing the observed time series at multiyear resolutions. While the error analysis here was based on a limited sample (mainly due to the short duration of the satellite period), these results suggested that the proposed stochastic downscaling mechanism is quite robust in reproducing the monthly statistics of globally averaged precipitation, with only moderate sensitivity to the coarse-resolution forcing.

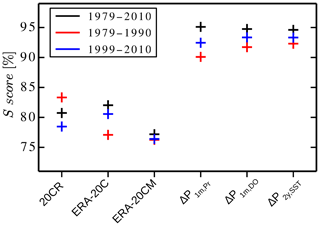
Figure 6 S score computed from the different P simulations against GPCP. The values estimated for the full satellite period (1979–2010) are presented in black, for the 1979–1990 period are presented in red, and for the 1990–2010 period are presented in blue. For the ERA-20CM dataset, the S score is estimated from the 10-member ensemble PDF.

6 Discussion and conclusions

Atmospheric variables display significant variability over a wide range of temporal scales due to changes in external forcings (including surface fluxes, changes to greenhouse gases and aerosol concentrations, solar forcing, and volcanic eruptions), but also due to intrinsic modes of atmospheric variability. Additionally, external and internal atmospheric processes interact nonlinearly amongst themselves, resulting in an intricate multi-scale structure, which is still ill understood and responsible for significant uncertainties in climate models. Here a multi-scale analysis framework was employed, aiming to disentangle the complex structure of globally averaged precipitation variability.

The multi-scale correlation structure obtained from Haar fluctuations suggested that global-mean precipitation variability at multiyear timescales is linearly related to the net atmospheric radiative fluxes, corresponding to the dominant effect of energetic constraints on precipitation variability. Furthermore, this linear relationship is dominated by its longwave component and, more specifically, by the surface longwave radiative fluxes, particularly DLR. The results also suggest that clouds play a negligible role in these linear correlations at multiyear scales.

Building on the previous works of Lovejoy et al. (2017) and Nogueira (2019), the present paper highlights a critical transition in the multi-scale correlation structure at timescales of ∼1 year, revealing a change in the control mechanisms of several atmospheric variables, including precipitation. Specifically, at multiyear timescales the following is true: (i) globally averaged precipitation becomes tightly correlated with the net atmospheric radiative fluxes ($\left|\mathit{\rho }\right|\mathrm{0.8}$), and this correlation is dominated by the downwelling longwave radiative flux at the surface; (ii) the cloud effects on the atmospheric radiative fluxes in (i) can be neglected; and (iii) globally averaged precipitable water vapor becomes tightly correlated (ρ∼0.9) with surface temperature. The respective sensitivity coefficient for multiyear fluctuations of precipitable water vapor to surface temperature is estimated here to be 0.07 % K⁻¹, close to the value predicted by the Clausius–Clapeyron relationship. (iv) Globally averaged SST and near-surface air temperature over land become strongly correlated (ρ∼0.7), implying a strong atmosphere–ocean coupling in agreement with and extending the results from Lovejoy et al. (2017) based on one observational dataset. In contrast, at sub-yearly timescales, the magnitude of all these correlations decreases abruptly towards negligible values, and cloud effects are no longer negligible in the correlations between atmospheric radiative fluxes and precipitation. Hints of a similar, but less robust, transition also emerged for the correlation structure between globally averaged precipitation and surface temperature, with negligible correlations at sub-yearly timescales, which tend increase at multiyear timescales, although the latter displayed significant spread amongst different datasets (ranging between ∼0.4 and ∼0.7).

The transition found here also contributes to sharpening the picture from previous studies reporting a “slow” response, in which globally averaged precipitation increases due to increasing surface temperature, and a “fast” response, in which the atmosphere rapidly adjusts to changes in top-of-atmosphere radiative forcing, and that is independent of temperature fluctuations (Allen and Ingram, 2002; Bala et al., 2010; Andrews et al., 2010; O'Gorman et al., 2012; Allan et al., 2014). The correlation structure found here suggests that the slow component corresponds to multiyear timescales and that radiative constraints (particularly surface longwave fluxes) are the key mechanism controlling precipitation variability rather than temperature, while cloud effects are negligible. On the other hand, the correlations here confirm the breakdown of the linear relation between temperature fluctuations at fast (sub-yearly) timescales, but the dominant effect of top-of-atmosphere radiative forcing is not evident and, most likely, the situation is much more complex (for example, surface sensible heat fluxes seem to become relevant at these timescales).

The robustness of this emergent multi-scale correlation structure is demonstrated by proposing simple models for the reconstruction of globally averaged precipitation at multiyear timescales. Anomaly time series for globally averaged precipitation at 2-year resolution were derived from SST observations alone, either directly based on precipitation vs. SST correlation structure or by combining the more robust energetic constraints of globally averaged precipitation (namely the precipitation vs. clear-sky DLR correlation) with an empirical algorithm for clear-sky DLR estimation and the Clausius–Clapeyron relationship. After correcting for their systematic mean bias, the highly idealized model for ΔP_2 y based on clear-sky DLR estimated from the Prata algorithm displayed similar accuracy in reproducing observations as atmospheric-model-based products, as measured by RMSE_bc, the Pearson correlation coefficient, and normalized standard deviation. Finally, the model based on precipitation vs. SST correlation showed the weakest performance, which agrees with the less robust correlations underlying this idealized model.

The proposed linear models cannot be extended to sub-yearly timescales because all the correlations upon which they rely become negligible. This abrupt transition in the multi-scale correlation structure implies that at sub-yearly timescales the tight linear coupling between atmospheric and ocean temperature, the Clausius–Clapeyron relationship, and the atmospheric energy balance are no longer dominant linear constraints for globally averaged precipitation. Nonetheless, the multi-scale analysis framework provides another path for the reconstruction of precipitation statistics at sub-yearly resolution. A stochastic downscaling algorithm based on scale-invariant symmetries of precipitation was applied to ΔP_2 y reconstructed time series, resulting in monthly globally averaged precipitation PDFs. Remarkably, the reconstructed PDFs at monthly resolution showed better accuracy in reproducing observed statistics than atmospheric-model-based products, as measured by the PDF matching S score computed over decadal and 30-year periods. These results highlight the relevance and potential applications of multi-scale frameworks for atmospheric sciences.