Thermodynamics of saline and fresh water mixing in estuaries

The mixing of saline and fresh water is a process of energy dissipation. The freshwater flow that enters an estuary from the river contains potential energy with respect to the saline ocean water. This potential energy is able to perform work. Looking from the ocean to the river, there is a gradual transition from saline to fresh water and an associated rise in the water level in accordance with the increase in potential energy. Alluvial estuaries are systems that are free to adjust dissipation processes to the energy sources that drive them, primarily the kinetic energy of the tide and the potential energy of the river flow and to a minor extent the energy in wind and waves. Mixing is the process that dissipates the potential energy of the fresh water. The maximum power (MP) concept assumes that this dissipation takes place at maximum power, whereby the different mixing mechanisms of the estuary jointly perform the work. In this paper, the power is maximized with respect to the dispersion coefficient that reflects the combined mixing processes. The resulting equation is an additional differential equation that can be solved in combination with the advection–dispersion equation, requiring only two boundary conditions for the salinity and the dispersion. The new equation has been confronted with 52 salinity distributions observed in 23 estuaries in different parts of the world and performs very well.

1 Introduction

The mixing of fresh and saline water in estuaries is governed by the dispersion–advection equation, which results from the combination of the salt balance and the water balance under partial to well-mixed conditions (see e.g. Savenije, 2005). The partially to well-mixed condition applies when the increase in the salinity over the estuarine depth is gradual. The salinity equation reads

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle }A{\displaystyle \frac{\partial S}{\partial t}}+Q{\displaystyle \frac{\partial S}{\partial x}}-{\displaystyle \frac{\partial }{\partial x}}\left(AD{\displaystyle \frac{\partial S}{\partial x}}\right)=\mathrm{0}.\end{array}$$

Here, S [psu] is the salinity of the water, Q [L³ T⁻¹] is the water flow in the estuary, A [L²] is the cross-sectional area of the flow (not necessarily equal to the storage cross section A_S), x is the distance from the estuary mouth, and D [L² T⁻¹] is the dispersion coefficient. The first term reflects the change in the salinity over time as a result of the balance between the advection by the water flow (second term) and the mixing of water with different salinity by dispersive exchange flows (third term). If there is no other source of salinity, then the sum of these terms is zero. If we average this equation over a tidal period, then the first term reflects the long-term change in the salinity as a result of the balance between the advection of fresh water from the river and the tidal average exchange flows. In a steady state in which the first term is zero, the equation can be simply integrated with respect to x, yielding

$$\begin{array}{}\text{(2)}& {\displaystyle }Q\left(S-S_{\mathrm{f}}\right)-AD{\displaystyle \frac{\mathrm{d}S}{\mathrm{d}x}}=\mathrm{0},\end{array}$$

with the condition that at the upstream boundary dS∕dx = 0 and S = S_f, which is the salinity of the fresh river water. In the steady-state situation the discharge Q then equals the freshwater discharge coming from upstream, which has a negative value moving seaward; similarly the salinity gradient S^′ = dS∕dx is negative with the salinity decreasing in the upstream direction. Assuming that in a given estuary the geometry A(x) is known, as is the observed salinity and discharge of the fresh river water, then this differential equation has two unknowns D(x) and S(x).

Figure 1 System description of the salt and fresh water mixing in an estuary, with the seaside on the left and the riverside on the right. The water level (blue line) has a slope as a result of the salinity distribution (red line). In yellow are the hydrostatic pressure distributions on both sides. The black arrows show the fluxes. Subscript “0” represents the downstream boundary condition.

In the steady state, the flushing out of salt by the fresh river discharge is balanced by the exchange of saline and fresh water resulting from a combination of mixing processes, which causes an upriver flux of salt. The sketch in Fig. 1 presents the system description with a typical longitudinal salinity distribution (in red). It also shows the associated water level (in blue), which has an upstream gradient due to the decreasing salinity. Because of the density difference, the hydrostatic pressures on both sides (in yellow) are not equal. The water level at the toe of the salt intrusion curve is Δh higher, resulting in a seaward pressure difference near the surface and an inland pressure difference near the bottom. Although the hydrostatic forces (the integrals of the hydrostatic pressure distributions) are equal and opposed in steady state, they have different working lines that are a distance Δh∕3 apart. This triggers an angular momentum, which drives the gravitational circulation.

The dispersion coefficient of Eq. (2) is generally determined by calibration on observations of S(x) or predicted by (semi-)empirical methods. Providing a theoretical basis for the dispersion coefficient is not trivial. A fundamental question is what this dispersion actually is. Is it a physical parameter, or merely a parameter that follows from averaging the complex turbulent flow patterns in a natural watercourse? MacCready (2004), for instance, was able to derive an analytical expression for the dispersion as a function of the salinity gradient in addition to geometric, hydraulic, and turbulence parameters. But this derivation also required simplifying assumptions.

The complication is that there are many different mixing processes at work. One can distinguish tidal shear, tidal pumping, tidal trapping, gravitation circulation (e.g. Fischer et al., 1979), and residual circulation due to the interaction between ebb and flood channels (Nguyen et al., 2008; Zhang and Savenije, 2017). And these different processes can be split up in many subcomponents. Park and James (1990), for instance, distinguished 66 components grouped into 11 terms. This reductionist approach, unfortunately, did not lead to more insight.

2 Applying thermodynamics to salt and fresh water mixing

Here we take a system approach in which the assumption is that the different mechanisms are not independent but are jointly at work to reduce the salinity gradient that drives the exchange flows. We use the concept of maximum power as described by Kleidon (2016). Kleidon defines Earth system processes as dissipative systems that conserve mass and energy, but export entropy. These systems tend to function at maximum power, whereby the power of the system can be defined as the product of a process flux and the gradient driving the flux. The ability to maintain this power (i.e. work through time) in steady state results from the exchange fluxes at the system boundary, and when work is performed at the maximum possible rate within the system (“maximum power”), this equilibrium state reflects the conditions at the system boundary. The key parameter describing the process can then be found by maximizing the power.

From an energy perspective, we see that the freshwater flux, which has a lower density than saline water and without a counteracting process would float on top of the saline water, adds potential energy to the system, while the tide, which flows in and out of the estuary at a regular pace, creates turbulence, mixes the fresh and saline water, and hence works at reducing this potential energy. This is why dispersion predictors are generally linked to the estuarine Richardson number, which represents the ratio of the potential energy of the fresh water entering the estuary to the kinetic energy of the tidal flow.

In thermodynamic terms, the freshwater flux maintains a potential energy gradient, which triggers mixing processes that work at depleting this gradient. Because the strength of the mixing of fresh and saline water in turn depends on this gradient, there is an optimum at which the mixing process performs at maximum power. From a system point of view, it is not really relevant which particular mixing process is dominant or how these different processes jointly reduce the salinity gradient. What is relevant is how the optimum flux associated with this mixing process, yielding maximum power, depends on the dispersion.

In our case, the power derived from the potential energy of the freshwater flux is described by the product of the upstream dispersive water flux and the gradient in geopotential height driving this flux or, alternatively, the product of the dispersive exchange flux and the water level gradient. The optimum situation is achieved when the system is in an equilibrium state.

The water level gradient follows from the balance between the hydrostatic pressures of fresh and saline water (see e.g. Savenije, 2005), resulting in

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{\mathrm{d}z}{\mathrm{d}x}}=-{\displaystyle \frac{h}{\mathrm{2}\mathit{\rho }}}{\displaystyle \frac{\mathrm{d}\mathit{\rho }}{\mathrm{d}x}},\end{array}$$

where z (= h + Δh) [L] is the tidal average water level (blue line in Fig. 1), h [L] is the tidal average water depth (horizontal dashed line in Fig. 1), and ρ [M L⁻³] is the depth average density of the saline water. The depth gradient is essential for the density-driven mixing, but Δh is small compared to h (typically 1.2 % of h). Note that this equation applies to the case in which the river flow velocity is small, which is the case when estuaries are well mixed. Otherwise a backwater effect should be included, but this only applies to a situation of high river discharge when the salt intrudes by means of a salt wedge with a sharp interface.

One can express the density of saline water as a function of the salinity: ρ = 1000 + α₁S, where α₁ is a constant with a value of about 25∕35 because seawater with a salinity of 35 psu has a density of about 1025 kg m⁻³. As a result, Eq. (3) can be written as

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle \frac{\mathrm{d}z}{\mathrm{d}x}}=-{\mathit{\alpha }}_{\mathrm{1}}{\displaystyle \frac{h}{\mathrm{2}\mathit{\rho }}}{S}^{\prime }.\end{array}$$

The upstream dispersive flux is implicit in the salt balance Eq. (2), which in steady state can be written as

$$\begin{array}{}\text{(5)}& {\displaystyle }{\displaystyle }Q\left(S-S_{\mathrm{f}}\right)=AD{S}^{\prime }.\end{array}$$

The left-hand term is the salt flux due to the fresh water of the river that pushes back the salt, whereas the right-hand term is the dispersive intrusion of salt due to the exchange flux of the combined mixing processes (see Fig. 1). Writing both sides as water fluxes results in

$$\begin{array}{}\text{(6)}& {\displaystyle }{\displaystyle }Q={\displaystyle \frac{AD{S}^{\prime }}{\left(S-S_{\mathrm{f}}\right)}}.\end{array}$$

The right-hand side is the water exchange flux, which is the flux that depletes the gradient. As Eq. (6) shows, in steady state this exchange flux is equal to the freshwater discharge. The combination of the flux and the gradient leads to the power of the mixing system per unit length (defined as a positive quantity):

$$\begin{array}{}\text{(7)}& {\displaystyle }{\displaystyle }P=-\mathit{\rho }gQ{\displaystyle \frac{\mathrm{d}z}{\mathrm{d}x}}={\mathit{\alpha }}_{\mathrm{1}}Q{\displaystyle \frac{gh}{\mathrm{2}}}{S}^{\prime }.\end{array}$$

Applying the theory of maximum power to the dispersive process, we need to maximize the power with regard to the dispersion coefficient, which is the parameter representing the mixing and which is the main unknown in salt intrusion prediction:

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{\mathrm{d}P}{\mathrm{d}D}}=\mathrm{0}.\end{array}$$

Applying Eq. (8) with constant river discharge Q and constant depth h, which is the property of an ideal alluvial estuary according to Savenije (2005), leads to

$$\begin{array}{}\text{(9)}& {\displaystyle }{\displaystyle \frac{\mathrm{d}{S}^{\prime }}{\mathrm{d}D}}=\mathrm{0}.\end{array}$$

Using the salt balance equation where S^′ = Q(S − S_f)∕(AD), differentiation leads to

$$\begin{array}{}\text{(10)}& {\displaystyle }{\displaystyle \frac{\mathrm{d}{S}^{\prime }}{\mathrm{d}D}}={\displaystyle \frac{\mathrm{d}{S}^{\prime }}{\mathrm{d}x}}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}D}}={\displaystyle \frac{Q}{AD}}\left\{{\displaystyle \frac{S^{\prime }}{D^{\prime }}}-{\displaystyle \frac{A^{\prime }\left(S-S_{\mathrm{f}}\right)}{A{D}^{\prime }}}-{\displaystyle \frac{\left(S-S_{\mathrm{f}}\right)}{D}}\right\},\end{array}$$

where the prime means the gradient of the parameters with respect to x. The application of Eq. (9) then yields

$$\begin{array}{}\text{(11)}& {\displaystyle }{\displaystyle \frac{D{S}^{\prime }}{\left(S-S_{\mathrm{f}}\right)D^{\prime }}}={\displaystyle \frac{A^{\prime }D}{A{D}^{\prime }}}+\mathrm{1}.\end{array}$$

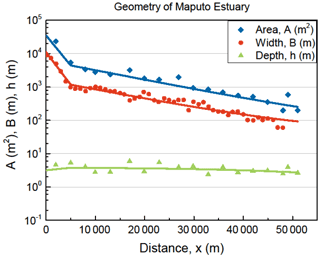
Figure 2 Geometry of the Maputo Estuary, showing the cross-sectional area A (blue diamonds), the width B (red dots), and the depth h (green triangles) on a logarithmic scale as a function of the distance from the mouth. The inflection point at x₁ = 5000 m separates the lower segment with a convergence length of a₀ = 2300 m from the upper segment with a₁ = 16 000 m.

We introduce three length scales: a = −(A − $A_{\mathrm{f}})/A^{\prime }$, s = −(S − $S_{\mathrm{f}})/S^{\prime }$, and d = $-D/D^{\prime }$, where a is the convergence length of an exponentially varying estuary cross section which tends towards the cross section of the river A_f, s is length scale of the longitudinal salinity variation, and d is length scale of the longitudinal variation of dispersion. In macro-tidal estuaries, the part of the estuary where the salt intrusion occurs has a much larger cross section than the upstream river such that A_f ≪ A and a ≈ $-A/A^{\prime }$. In riverine estuaries where this is not the case, a factor ε = (1 − A_f∕A) should be included. All length scales have the dimension of [L]. In an exponentially shaped estuary, the convergence length a is a constant, but d and s vary with x. It can be shown that the proportion s∕d equals the Van der Burgh coefficient K (= $A{D}^{\prime }/Q$) (Van der Burgh, 1972), which in this approach varies as a function of x, although it is generally assumed as constant (e.g. Savenije, 2005; Zhang and Savenije, 2017). Using these length scales, Eq. (11) can be written as

$$\begin{array}{}\text{(12a)}& {\displaystyle }{\displaystyle \frac{s}{d}}={\displaystyle \frac{a}{a+d\mathit{\epsilon }}},\end{array}$$

or

$$\begin{array}{}\text{(12b)}& {\displaystyle }{\displaystyle }s={\displaystyle \frac{ad}{a+d\mathit{\epsilon }}},\end{array}$$

or

$$\begin{array}{}\text{(12c)}& {\displaystyle }{\displaystyle }d={\displaystyle \frac{as}{a-s\mathit{\epsilon }}},\end{array}$$

where in estuaries with a pronounced funnel shape, ε ≈ 1. Equation (12) is an additional equation to the salt balance, which in terms of the length scales reads s = $-AD/Q$. As a result, we have two differential equations with two unknowns: S(x) and D(x). Adding two boundary conditions at a given point S₀ and D₀ would solve the system. The first boundary condition is simply the sea salinity if the boundary is chosen at the estuary mouth. Then the only unknown parameter left is the value for the dispersion at the boundary. For this boundary value, empirical predictive equations have been developed which relate the D₀ to the estuarine Richardson number (e.g. by Gisen et al., 2015), which goes beyond this paper. If observations of salinity distributions are available, then the value of D₀ is obtained by calibration.

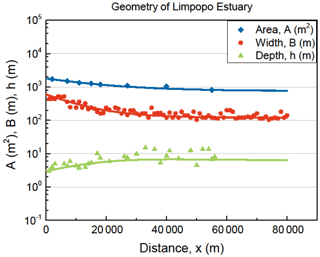
Figure 3 Geometry of the Limpopo Estuary, showing the cross-sectional area A (blue diamonds), the width B (red dots), and the depth h (green triangles) on a logarithmic scale as a function of the distance from the mouth. There is no inflection point, but the estuary converges exponentially towards the river cross section A_f = 800 m², with a convergence length of 20 km.

What the maximum power equation has contributed is that it provides an additional equation. In the past, a solution could only be found if an empirical equation was added describing D(x), containing an additional calibration parameter. In the approach by Savenije (2005) this was the empirical Van der Burgh equation containing the constant Van der Burgh coefficient K. However, with the new Eq. (12), which in fact represents a spatially varying Van der Burgh coefficient, this additional calibration parameter is no longer required. So this thermodynamic approach replaces the empirical equation with a new physically based equation and removes a calibration parameter, leaving only one unknown: the dispersion at a well-chosen boundary condition.

3 Application

The two Eqs. (2) and (12) together can be solved numerically by using a simple linear integration scheme. As a boundary condition it requires values for S₀ and D₀ at a well-chosen location. In alluvial estuaries the cross-sectional area A(x) generally varies according to an exponential function which often has an inflection point (see, for example, Fig. 2 describing the Maputo Estuary in Mozambique). The boundary condition is best taken at this inflection point (x = x₁) if the estuary has one. If the estuary has no inflection point, as is the case in the Limpopo estuary (see Fig. 3), then the boundary condition is taken at the estuary mouth (x = 0).

The downstream part of estuaries with an inflection point has a much shorter convergence length, giving the estuary a typical trumped shape. This wider part is generally not longer than about 10 km, which is the distance over which ocean waves dissipate their energy. Beyond the inflection point, the shape is determined by the combination of the kinetic energy of the tide and the potential energy of the river flow. If the tidal energy is dominant over the potential energy of the river, then the convergence is short, leading to a pronounced funnel shape; if the potential energy of the river is large due to regular and substantial flood flows, then the convergence is large, which is typical for deltas. Hence, the topography can be described by two branches:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }A=A_{\mathrm{f}}+\left(A_{\mathrm{0}}-A_{\mathrm{f}}\right)\exp \left(-x/a_{\mathrm{0}}\right)\mathrm{if}\mathrm{0}<x<x_{\mathrm{1}}\\ \text{(13)}& {\displaystyle }& {\displaystyle }A=A_{\mathrm{f}}+\left(A_{\mathrm{1}}-A_{\mathrm{f}}\right)\exp \left(-\left(x-x_{\mathrm{1}}\right)/a_{\mathrm{1}}\right)\mathrm{if}x\ge x_{\mathrm{1}},\end{array}$$

where A₀ and A₁ are the cross-sectional areas at x = 0 and x = x₁, respectively, and a₀ and a₁ are the convergence lengths of the lower and upper segments. In some cases in which ocean waves do not penetrate the estuary, there is no inflection point and x₁ = 0. The Maputo (see Fig. 2) has two segments, whereas the Limpopo Estuary (see Fig. 3), an estuary in Mozambique 200 km north of the Maputo, is semi-closed by a sandbar and has a single branch. It can also be seen that in the Limpopo the size of the river cross section is not negligible and that ε < 1, showing a slight curve in the exponential functions.

Subsequently we have integrated Eqs. (2) and (12) conjunctively by using a simple explicit numerical scheme in a spreadsheet and confronted the solution with observations. The solutions are fitted to the data by selecting values for S and D at the boundary condition x = x₁ (or at x = 0 for the Limpopo). Figures 4 and 5 show applications of the solution to selected observations in the Maputo and Limpopo estuaries. In the Supplement more applications are shown, also for other estuaries in different parts of the world.

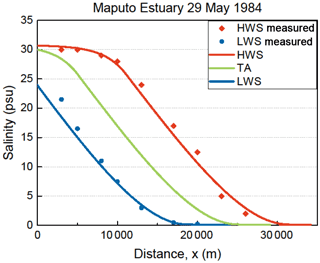
Figure 4 Application of the numerical solution to observations in the Maputo Estuary for high water slack (HWS) and low water slack (LWS). The green line shows the tidal average (TA) condition. The red diamonds reflect the observations at HWS and the blue dots the observations at LWS on 29 May 1984.

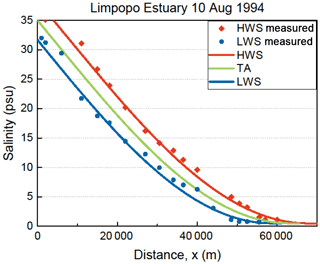
Figure 5 Application of the numerical solution to observations in the Limpopo Estuary for high water slack (HWS) and low water slack (LWS). The green line shows the tidal average (TA) condition. The red diamonds reflect the observations at HWS and the blue dots the observations at LWS on 10 August 1994.

4 Discussion and conclusion

By making use of the maximum power (MP) concept, it was possible to derive an additional equation to describe the mixing of salt and fresh water in estuaries. Together with the salt balance equation, these two first-order and linear differential equations only require two boundary conditions (the salinity and the dispersion at some well-chosen boundary) to be solved. If the estuary has an inflection point in the geometry, then the preferred boundary condition lies there; otherwise the boundary condition is chosen at the ocean boundary.

This new equation can replace previous empirical equations, such as the Van der Burgh equation, and does not require any calibration coefficients (besides the boundary conditions). The new equation appears to fit very well to observations, which adds credibility to the correctness of applying the MP concept to fresh and salt water mixing.

The method presented here is based on a system perspective, which is holistic rather than reductionist. Reductionist theoretical methods have tried to break down the total dispersion in a myriad of smaller mixing processes, some of which are difficult to identify or to connect to conditions that make them more or less prominent. The idea here is that in a freely adjustable system, such as an alluvial estuary, individual mixing processes are not independent of each other, but rather influence each other and jointly work at reducing the salinity gradient at maximum dissipation. The resulting level of maximum power and dissipation is set by the boundary conditions of the system. It is then less important which mechanism is dominant, as long as the combined performance is correct. The maximum power limit is a way to derive this joint performance of mixing processes. The fact that the relationship derived from maximum power works so well in a wide range of estuaries is an indication that natural systems evolve towards maximum power, much like a machine that approaches the maximum performance of the Carnot limit.

Appendix A: Notation

Table A1 Notation.