Potential effect of the marine carbon cycle on the multiple equilibria window of the Atlantic Meridional Overturning Circulation

The Atlantic Meridional Overturning Circulation (AMOC) is considered to be a tipping element in the Earth system due to possible multiple (stable) equilibria. Here, we investigate the multiple equilibria window of the AMOC within a coupled ocean circulation–carbon cycle box model. We show that adding couplings between the ocean circulation and the carbon cycle model affects the multiple equilibria window of the AMOC. Increasing the total carbon content of the system widens the multiple equilibria window of the AMOC, since higher-atmospheric pCO₂ values are accompanied by stronger freshwater forcing over the Atlantic Ocean. The important mechanisms behind the increase in the multiple equilibria window are the balance between the riverine source and the sediment sink of carbon and the sensitivity of the AMOC to freshwater forcing over the Atlantic Ocean. Our results suggest that changes in the marine carbon cycle can influence AMOC stability in future climates.

1 Introduction

The Atlantic Meridional Overturning Circulation (AMOC) plays a large role in modulating global climate (Vellinga and Wood, 2008; Palter, 2015) because it transports heat from the Southern Hemisphere to the Northern Hemisphere and is one of the prominent tipping elements in the Earth system (Lenton et al., 2008; Armstrong-McKay et al., 2022). Model studies suggest that the AMOC can have multiple stable equilibria, namely the “on” state, representing the current AMOC state with a strong northward flow at the surface and a southward return flow at intermediate depths, and the “off” state, representing a weak or even reversed AMOC state (Weijer et al., 2019). From a dynamical system point of view, a bi-stable AMOC regime appears through the occurrence of two saddle node bifurcations (Dijkstra, 2007), and the region in the parameter space where both on and off states co-exist is the multiple equilibria window (MEW), also referred to as the bi-stability window (Barker and Knorr, 2021).

Climate variability in the past, such as Heinrich events, has been linked to the tipping of the AMOC (Rahmstorf, 2002; Lynch-Stieglitz, 2017). Under anthropogenic forcing, the global warming threshold for AMOC tipping has recently been estimated to be around 4 °C (Armstrong-McKay et al., 2022). Recent studies suggest that the AMOC has been weakening (Caesar et al., 2018; Dima et al., 2021) and might even collapse in this century (Ditlevsen and Ditlevsen, 2023). Using model data from the Coupled Model Intercomparison Project 6 (CMIP6; Eyring et al., 2016), a consistent weakening of the AMOC under future climate change is projected (Weijer et al., 2020), with a 34 %–45 % decrease in AMOC strength in 2100, but no clear tipping was found. However, these models may have an AMOC that is too stable (Weijer et al., 2019), thus affecting the probability of AMOC tipping before 2100. Under AMOC tipping, a strong cooling in the Northern Hemisphere (Rahmstorf, 2002; Drijfhout, 2015), changes in the water cycle (Vellinga and Wood, 2002; Jackson et al., 2015), and potential interactions with other tipping elements in the Earth system (Dekker et al., 2018; Wunderling et al., 2021; Sinet et al., 2023) are expected.

The AMOC can also interact with the marine carbon cycle and therefore influence atmospheric pCO₂. By affecting the transport of important tracers, such as dissolved inorganic carbon (DIC), total alkalinity, and nutrients, the AMOC affects the solubility and biological carbon pumps. Evidence of couplings between the AMOC and marine carbon cycle is provided in proxy data (Bauska et al., 2021). Model studies show a wide range of potential carbon cycle responses to a collapse of the AMOC. While most models show an increase in atmospheric pCO₂ (e.g., Marchal et al., 1998; Schmittner and Galbraith, 2008; Matsumoto and Yokoyama, 2013; Boot et al., 2024b), the magnitude and precise mechanisms are dependent on the model used and the climatic boundary conditions (Gottschalk et al., 2019).

As the AMOC can influence atmospheric pCO₂, there is a potential feedback mechanism since atmospheric pCO₂ influences the hydrological cycle (Weijer et al., 2019; Barker and Knorr, 2021), which, through changes in buoyancy fluxes, affects the AMOC. Previous studies, mostly focused on proxy data, suggest that there may be a relation between atmospheric pCO₂ and the MEW of the AMOC (Barker et al., 2010, 2015). However, a clear mechanistic view has not been given yet. Here, we study the mechanisms of how the marine carbon cycle can affect the MEW of the AMOC using a coupled ocean circulation–carbon cycle box model.

2 Methods

We have coupled a box model suitable for simulating AMOC dynamics (Sect. 2.1) to a carbon cycle box model (Sect. 2.2). To be able to accurately represent atmospheric CO₂ concentrations, the coupled model extends the AMOC box model by including boxes that represent the Indo-Pacific. Steady states of the coupled model, where several non-linear couplings are implemented (Sect. 2.3), are determined using continuation software (Sect. 2.4). Parameter values and model equations are described in Appendix B and C.

2.1 AMOC box model

The box model (Cimatoribus et al., 2014; Castellana et al., 2019) representing the AMOC dynamics simulates the depth of the Atlantic Ocean pycnocline and the distribution of salt in the Atlantic Ocean and the Southern Ocean. It consists of five boxes, with six prognostic variables. The northern box n represents the regions of deep-water formation in the North Atlantic, and box s represents the entire Southern Ocean (i.e., all longitudes). There are two thermocline boxes, t and ts, where box ts represents the region between 30 and 40° S which is characterized by strong sloping isopycnals, where the pycnocline becomes shallower moving poleward. Underneath the four surface boxes, there is one box (d) representing the deep ocean.

The distribution of salinity in the boxes is dependent on the ocean circulation and surface freshwater fluxes. In the Southern Ocean, there is wind-induced Ekman transport into the Atlantic (q_Ek), and there is an eddy-induced transport from the Atlantic into the Southern Ocean (q_e) which is dependent on the pycnocline depth, D. The difference between the two, defined as $q_{\mathrm{S}}=q_{\mathrm{e}}-q_{\mathrm{Ek}}$, represents upwelling in the Southern Ocean and net volume transport into the Atlantic thermocline. The thermocline also is sourced with water from box d through diffusive upwelling (q_U). The strength of the downward branch of the AMOC is represented in the North Atlantic by q_N. This downwelling is dependent on the meridional density gradient between box ts and box n, where the density is determined using a linear equation of state. Wind-driven gyre transport is modeled by r_N in the Northern Hemisphere and r_S in the Southern Hemisphere. Salinity is also affected by two surface freshwater fluxes, modeled as virtual salt fluxes. First, there is a symmetrical forcing, E_s; i.e., this freshwater flux is the same for both hemispheres; and second, there is an asymmetrical forcing, E_a, which results in interhemispheric differences. This last parameter can be viewed as a control parameter for the AMOC strength since it regulates the salinity of box n. The pycnocline depth is an important state variable in this model since several volume fluxes are dependent on it. This depth is dependent on four different volume fluxes going in and out of the two thermocline boxes of t and ts (q_e, q_Ek, q_U, and q_N).

The model provides a simple framework to study AMOC dynamics and has already been used to show the slow (Cimatoribus et al., 2014) and fast noise-induced (Castellana et al., 2019; Jacques-Dumas et al., 2023) tipping of the AMOC.

2.2 Carbon cycle model

The carbon cycle model is derived from the equations of the SCP-M (O'Neill et al., 2019). The original SCP-M has two terrestrial carbon stocks, an atmosphere box, and seven ocean boxes representing the global ocean. In the ocean, multiple tracers are simulated that are important for the marine carbon cycle. In this study, we only simulate dissolved inorganic carbon (DIC), alkalinity (Alk), and phosphate (PO₄) in the ocean. All three tracers are affected by ocean circulation, have a riverine source, and have a sink to the sediments. DIC is affected by biological production and remineralization (soft tissue pump), by the formation and dissolution of calcium carbonate (CaCO₃; carbonate pump), and by gas exchange with the atmosphere. Alk is also affected by the carbonate pump and PO₄ by the soft tissue pump. In this model, PO₄ is explicitly conserved; i.e., the source of PO₄ is equal to the sink of PO₄ at all times. DIC and Alk, however, can vary since the time-dependent riverine influx is not necessarily equal to the sediment outflux.

The soft tissue pump is modeled using constant values of export production per box, and the remineralization in the water column follows a power law (Martin et al., 1987). The influence of the soft tissue pump on the cycling of PO₄ is modeled using a constant stoichiometric ratio. The formation of CaCO₃ is proportional to the export production multiplied by a constant rain ratio parameter. CaCO₃ is dissolved through the water column and in the sediments. This dissolution is dependent on the CaCO₃ saturation state, and a constant background dissolution. The gas exchange between the ocean and atmosphere is dependent on a constant piston velocity and the difference in pCO₂ between the two reservoirs. The riverine influx of PO₄ is constant, whereas the influx of DIC and Alk is dependent on atmospheric pCO₂.

2.3 Coupled model

The two models described in the previous section are coupled to form the model used in this study (Fig. 1). For this, several parameter assumptions had to be made since the carbon cycle model requires more parameters than the AMOC model. First of all, the depth of boxes n and s is not given in Cimatoribus et al. (2014), but it is necessary for the carbon cycle model. We assume these depths to be 300 m, and the total depth of the ocean is assumed to be 4000 m. Second, a first version of the model showed a sensitivity of atmospheric CO₂ concentrations to AMOC tipping that is too strong, causing very low-CO₂ concentrations on the AMOC off branch. We therefore have included two additional boxes in the AMOC model representing the Indo-Pacific basin, namely box ps for the surface ocean and box pd for the deep ocean. In these boxes, the same carbon cycle processes are present as in the Atlantic Ocean and Southern Ocean boxes of the model. Between these two boxes, there is a bidirectional mixing term (γ₁=30 Sv), and the boxes are connected with the Southern Ocean through a global overturning circulation (GOC; ψ₁=18 Sv) and gyre-driven exchange (r_P=90 Sv). γ₁ and ψ₁ are taken from the SCP-M (O'Neill et al., 2019), and r_P is based on the model of Wood et al. (2019). Both boxes t and ps receive DIC, Alk, and PO₄ input through a riverine flux. The total riverine flux is modeled similarly in the SCP-M and is partitioned over the two boxes based on the volume fraction of the Atlantic Ocean and the Indo-Pacific Ocean, meaning that 20 % of the riverine flux flows into box t, while the remainder flows into box ps.

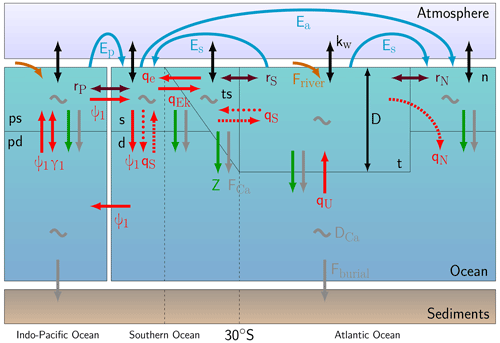
Figure 1 Box structure and processes simulated in the coupled circulation–carbon cycle model. Red arrows represent volume transports, where dashed arrows are only present during an on state, and dotted arrows are only present during an off state. The AMOC downwelling strength is represented by q_N and is determined through $\mathit{\eta }\frac{{\mathit{\rho }}_n-{\mathit{\rho }}_{ts}}{{\mathit{\rho }}_{\mathrm{0}}}{D}^{\mathrm{2}}$, where η is a hydraulic constant; ρ represents the density in boxes n (ρ_N) and ts (ρts) and a reference density (ρ₀). D represents the thermocline depth. The purple arrows represent gyre exchange (r_N, r_S, and r_P), and blue arrows represent freshwater fluxes (E_s, E_a, and E_p). Carbon cycle processes that are represented are riverine input (orange), air–sea gas exchange (black; k_w), biological export production (green; Z), CaCO₃ rain (grey; F_Ca), CaCO₃ dissolution (grey; D_Ca), and sediment burial (grey; F_burial). This figure is based on Castellana et al. (2019) and Boot et al. (2022).

The first coupling between the physical and the carbon cycle model is through the ocean circulation. The AMOC determined in the circulation model is used for the advective transport of the three tracers in the carbon cycle model. We have implemented additional coupling between the model and specific feedbacks within the carbon cycle model. Several of these feedbacks have been introduced into the SCP-M before (Boot et al., 2022).

Biological export production is constant in the SCP-M and therefore independent of available nutrients. This is a strong simplification of important processes in the real world that might not be valid in all cases. Therefore, we want to make the biological export production a function of nutrient availability. We do this by creating a dependency of the biological export production in the surface boxes to the amount of PO₄ advected into the specific surface box and therefore introducing a dependency on the ocean circulation as follows:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{Z}_i& =\left(\mathrm{1}-{\mathit{\lambda }}_{\mathrm{BI}}\right)\times Z_{i,\mathrm{base}}+{\mathit{\lambda }}_{\mathrm{BI}}\\ & \times \left(\sum _j\left(q_{j\to i}\times {\left[{\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}\right]}_j\right)+P_{\mathrm{river}}\right)\times {\mathit{ϵ}}_i.\end{array}\end{array}$$

Here Z_i represents the export production in surface box i. λ_BI is a parameter to switch between the default value of Z in box i (Z_i,base; λ_BI=0) and the variable export production (λ_BI=1). In addition, q_j→i represents the volume transport from box j into box i. P_river is the riverine influx of PO₄, which is only present in boxes t and ps, and ϵ_i represents a biological efficiency term in box i. i represents all surface boxes, i.e., n, t, ts, s, and ps. j can be any box and depends on the direction of the ocean circulation. In the text, we will refer to this coupling as the BIO coupling. Using this coupling, a weaker (stronger) ocean circulation would result in a reduced (increased) influx of nutrients, which causes a reduction (increase) in the biological carbon export from the surface to the deep ocean. This affects the carbon content in the surface ocean and carbon burial in the sediments.

We also introduce a coupling between the symmetric freshwater forcing E_s and atmospheric pCO₂. This coupling is based on a fit to an ensemble of CMIP6 Earth system models and is described in Sect. 3.1. We do this because we expect freshwater fluxes to change under different background climates (Galbraith and de Lavergne, 2019). The AMOC is dependent on E_s, and this coupling can therefore result in a changing AMOC under different pCO₂ values.

We allow the sea surface temperatures (SSTs) to vary with atmospheric pCO₂, following a logarithmic function and a climate sensitivity parameter, according to

$$\begin{array}{}\text{(2)}& {\displaystyle }{T}_i=T_{i,\mathrm{base}}+\mathrm{\Delta }{T}_i,\text{(3)}& {\displaystyle }\mathrm{\Delta }{T}_i={\mathit{\lambda }}_T\times \mathrm{0.54}\times \mathrm{5.35}\ln \left({\displaystyle \frac{{\mathrm{CO}}_{\mathrm{2}}}{{\mathrm{CO}}_{\mathrm{2},\mathrm{0}}}}\right).\end{array}$$

Here i represents the different surface ocean boxes. By varying the parameter λ_T, we are able to change the climate sensitivity of the model. In this study, we use a value of λ_T=0 (default); λ_T=1 (CS_LO); and a value of λ_T=2 (CS_HI), representing SST warming of 0, 2, and 4 K per CO₂ doubling. For the default values, sea surface temperature remains constant while independent of atmospheric pCO₂ values. For surface air temperature in CMIP6 models, the response to a CO₂ doubling is between 1.8 and 5.6 K (Zelinka et al., 2020). When this coupling is used, the changes in SSTs will also change the density in the ocean circulation model. However, since we use a linear equation of state, and the change in SST is homogeneous over all surface boxes, it does not influence the ocean circulation. In the text, we will refer to this coupling as the CS_LO and CS_HI couplings for the low and high climate sensitivity cases, respectively. This coupling introduces a positive feedback, namely higher-atmospheric pCO₂ values leading to the warming of the SSTs, which reduces the solubility of CO₂ in the ocean, meaning that more CO₂ will remain in the atmosphere. This feedback might be important for states where the CO₂ concentration deviates strongly from pCO_2,0.

Last, we have introduced a coupling on the rain ratio (Eq. 4), making it dependent on the saturation state of CaCO₃, following

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{F}_{\mathrm{Ca},i}& =\left(\mathrm{1}-{\mathit{\lambda }}_F\right)\times F_{\mathrm{Ca},\mathrm{base}}+{\mathit{\lambda }}_F\\ & \times \mathrm{0.022}{\left({\displaystyle \frac{\left[{\mathrm{Ca}}_i^{\mathrm{2}+}\right]\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]}{K_{sp,i}}}-\mathrm{1}\right)}^{\mathrm{0.81}},\end{array}\end{array}$$

where i represents the different surface ocean boxes. Similar to the biological coupling coefficient λ_BI, λ_F is either zero or one and including this feedback will introduce different rain ratios per box. This feedback is based on the work of Ridgwell et al. (2007), where the parameters 0.022 and 0.81 have been used as a calibration parameter in the GENIE-1 Earth system model. In the text, we will refer to this coupling as the FCA coupling. In this coupling, the rain ratio is increased if more carbonate is available, which represents higher calcification rates under such conditions. In our model, this affects the transfer of carbon and alkalinity from the surface ocean to the deep ocean and the sediments. This feedback is included because it can be important for the long timescales we investigate here.

We have included additional couplings in the model that are described in Appendix A. They are not included in the main text since they do not show large effects on the results. In the main text, only the couplings described above are used. We refer to the couplings as BIO for the biological coupling (BIO), E_s for the E_s coupling described in Sect. 3.1, FCA for the rain ratio coupling, CS_LO for a low climate sensitivity, and CS_HI for a high climate sensitivity.

As explained in the sections above, we have altered the box structure of both models and included several couplings and feedbacks in the model. These changes in the model can change the model dynamics compared to the original models, i.e., the AMOC box model (Cimatoribus et al., 2014; Castellana et al., 2019) and the SCP-M (O'Neill et al., 2019). Compared to the literature (Cimatoribus et al., 2014; Castellana et al., 2019), AMOC dynamics in our seven-box model are very similar to the dynamics in the original five-box model. The new box structure and ocean circulation change the carbon cycle quite a bit compared to the original SCP-M. To account for this, we have retuned the model before use, such that atmospheric pCO₂ is around pre-industrial values as detailed in Sect. 2.4. However, the most important aspects of the SCP-M are the carbon cycle dynamics. When no couplings are used, these are still the same. When couplings are introduced, the model is changed further, and the effects of these changes are one of the aspects we investigate in this study.

2.4 Solution method

The coupled model is a system of 30 ODEs (four tracers per box, with the pycnocline depth and atmospheric pCO₂) with the form

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{\mathrm{d}\mathit{u}}{\mathrm{d}t}}=f\left(\mathit{u}\right(t),\mathit{p}).\end{array}$$

Here u is the state vector (containing all the dependent quantities in all boxes), f refers to the right-hand side of the equation, and p is the parameter vector. To solve this system of equations, we use the continuation software AUTO-07p (Doedel et al., 2007). The AMOC model (Cimatoribus et al., 2014) and the SCP-M model (Boot et al., 2022) have already been implemented in this software. AUTO-07p enables us to efficiently compute branches of stable and unstable steady-state solutions under a varying control parameter. Furthermore, it allows the detection of special points such as saddle node bifurcations, which are important here for determining the multiple equilibria window of the AMOC.

One of the requirements of AUTO-07p is that the Jacobian determinant of the system (Eq. 5) is non-singular at non-bifurcation points. To achieve this, we use explicit conservation equations to eliminate the ODEs of the deep-Atlantic box (d). The conservation equation of salt and PO₄ are already explicitly included into the model. However, as described previously, this is not the case for DIC and Alk. Therefore, we have to introduce extra ODEs describing the change in total carbon and alkalinity in the system. The change in total carbon (DIC + atmospheric CO₂) and Alk in the atmosphere–ocean system can be captured as the sum of riverine influx and the sediment outflux. The riverine influx is a function of atmospheric pCO₂ and represents the weathering of silicate and carbonate rocks, i.e.,

$$\begin{array}{}\text{(6)}& C_{\mathrm{river}}=W_{\mathrm{carb},\mathrm{c}}+\left(W_{\mathrm{carb},\mathrm{v}}+W_{\mathrm{si}}\right)\times {\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}.\end{array}$$

The sediment outflux of DIC is determined by the sum of the soft tissue and the carbonate pumps over the entire ocean. In this model, all produced organic matter is also remineralized in the water column, causing the contribution of the soft-tissue pump to be negligible, resulting in

$$\begin{array}{}\text{(7)}& C_{\mathrm{sed}}=C_{\mathrm{river}}\times V_t+\sum _{i=\mathrm{1}}^{\mathrm{7}}\left(C_{\mathrm{carb},i}\times V_i\right).\end{array}$$

Since the change in alkalinity in the system is proportional to the change in total carbon, only one extra ODE is necessary. By eliminating the ODEs for the deep box and introducing the ODE for total carbon in the ocean–atmosphere system, AUTO-07p eventually solves a system with 27 ODEs.

The use of AUTO-07p made it necessary to make changes to the carbonate chemistry of the carbon cycle model. In the original SCP-M, a simple time-dependent function is used, where the pH of time step k−1 is used as an initial guess for time step k (Follows et al., 2006). As long as the changes per time step remain relatively small, this scheme is sufficiently accurate. However, due to our solution method, in which steady states are calculated against parameters, this function is not suitable for this study. Therefore, we have chosen a simple “textbook” carbonate chemistry (Williams and Follows, 2011; Munhoven, 2013), where Alk is assumed to be equal to carbonate alkalinity (Alk_carb= [HCO${}_{\mathrm{3}}^{-}$] + [CO${}_{\mathrm{3}}^{\mathrm{2}-}$]). This method is less accurate and leads to higher pH values (Munhoven, 2013) and lower-atmospheric pCO₂ values (Boot et al., 2022). To address the resulting lower-atmospheric pCO₂ values, we have increased the value of the constant rain ratio from 0.07 as used in the original SCP-M to 0.15.

AUTO-07p has three parameters that determine the accuracy of the solution. The absolute and relative accuracy are set to a base value of 10⁻⁶, but sometimes a higher accuracy is used. The accuracy for the detection of special points (e.g., saddle nodes and Hopf bifurcations) is set to 10⁻⁷.

3 Results

3.1 CMIP6 freshwater fluxes

The freshwater fluxes E_s and E_p used in the model are constrained using results from a CMIP6 ensemble. For this, we use 28 different CMIP6 models forced with a 1 % increase per year in atmospheric CO₂ concentrations (“1pctco2”). We integrate the variables “wfo” (water flux) and “vsf” (virtual salt flux) over the regions representing the Atlantic thermocline (Atlantic basin between 50° N and 30° S) and the Indo-Pacific basin (the rest of the ocean south of 66° N and north of 30° S) in the coupled box model. Based on these 28 models, we determine a multimodel mean, and we are able to constrain both E_p and E_s. For a full list of the models and used ensemble members, see Table D1.

Figure 2a shows that most models, and the multimodel mean, show no, or at most a very weak relation between E_p and atmospheric pCO₂, whereas there seems to be a relation between E_s and atmospheric pCO₂. For E_p, we will use the mean value over the entire simulation (0.99 Sv). For E_s, we will use as a default value 0.39 Sv, since this is the value of E_s at pCO_2,0 (320 ppm). Furthermore, we introduce an additional coupling in the model, where we implement E_s as a function of atmospheric pCO₂ based on a logarithmic fit to represent the relation between E_s and atmospheric pCO₂ present in the CMIP6 ensemble. This relation is modeled as

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{E}_{\mathrm{s}}& =\left(\mathrm{1}-{\mathit{\lambda }}_E\right)\times E_{\mathrm{s},\mathrm{base}}+{\mathit{\lambda }}_E\\ & \times \left(-\mathrm{0.142}+\mathrm{0.092}\times \ln \left({\mathrm{CO}}_{\mathrm{2}}\right)\right).\end{array}\end{array}$$

Here λ_E is a parameter controlling whether the coupling is used (λ_E=1) or the default value of E_s,base (0.39 Sv) is used (λ_E=0). Compared to earlier versions of the model, we will use a different default value for E_s. In previous studies, values of 0.25 Sv (Cimatoribus et al., 2014) and 0.17 Sv (Castellana et al., 2019) have been used. Here we choose the default value based on the value of E_s at an atmospheric pCO₂ value of 320 ppm (pCO_2,0) in the CMIP6 fit. The value of 0.39 Sv is of the same order as seen in the HOPAS4.0 dataset, based on satellite observations (Andersson et al., 2017). This dataset shows a net freshwater flux of 1 Sv averaged over the period 1987–2015 into the region representing the thermocline box, which results in an E_s value of 0.5 Sv. In the text, we will refer to this coupling as the E_s coupling. Note that this fit does not necessarily represent a direct causal relation between atmospheric pCO₂ and the freshwater flux. Surface temperature could also play an important role here. However, we have included the effects of temperature changes in relation to CO₂ through the CS coupling. The E_s coupling is responsible for the changes in salinity related to different CO₂ concentrations.

We have made two important choices for using these CMIP6-constrained freshwater fluxes. First of all, we set the freshwater transport through the atmosphere from the Atlantic to the Indo-Pacific basin to 0. There are studies showing there is moisture transport between the two basins through the atmosphere (e.g., Dey and Döös, 2020), but it is challenging to constrain this flux from Earth system models. However, in our model set-up, the exact value of this flux is not relevant for our results. The total freshwater flux integrated over the Indo-Pacific basin diagnosed from the CMIP6 ensemble is independent from the moisture transport between the Atlantic and Indo-Pacific basin. By rescaling the freshwater flux from the Indo-Pacific basin (box ps) to the Southern Ocean (box s), we can set the freshwater flux from the Atlantic to the Indo-Pacific to zero without changing the AMOC dynamics. Tests in which this flux was not set to zero but where the net evaporation out of boxes t and ps were kept constant show this result. The only effect of this freshwater transport is a shift in the diagram along the E_a axis and a small effect on atmospheric pCO₂ of a couple of parts per million (ppm) due to salinity changes.

The second choice we have made is that the net evaporation from the Atlantic thermocline is symmetrically divided over the northern and southern high latitudes. For this model, the exact direction of the freshwater flux out of box t is irrelevant. What is relevant is the total freshwater flux at each surface box. Through this, we can see that the asymmetric freshwater flux, E_a, creates an asymmetry in freshwater forcing over the Atlantic basin. Therefore, E_a creates the asymmetry that is potentially more realistic. Since we use E_a as our control parameter in the continuations, we do not need to constrain this parameter.

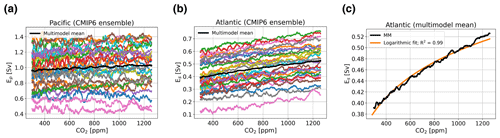
Figure 2 (a) Net evaporation from the Indo-Pacific basin representing the freshwater flux E_p (in Sv) for the CMIP6 ensemble, with the multimodel mean in black. (b) As in panel (a) but for the freshwater flux E_s. (c) The multimodel mean for E_s in black, with a logarithmic fit in orange.

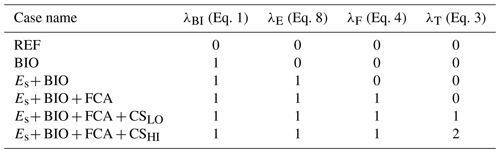
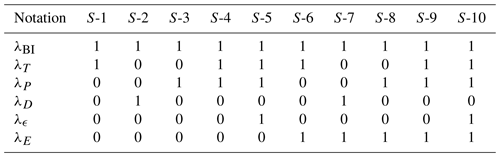
Table 1 Overview of the used cases. The left column represents the name of the case. The other columns represent whether a coupling denoted in the top row is used in the case mentioned in the first column by indicating the λ parameter associated with the coupling. For λ_T, the value represents the strength of the coupling. The quantity λ_BI refers to Eq. (1) (biological coupling), λ_E to Eq. (8) (E_s coupling), λ_F to Eq. (4) (rain ratio feedback), and λ_T to Eq. (3) (temperature).

3.2 The AMOC multiple equilibria window

We use several different model configurations that are differentiated on feedbacks and couplings included (see Table 1). We use these different configurations to show the effect on non-linear feedbacks on the MEW. Note that different couplings (see Appendix A) and different combinations of couplings are possible, but we have chosen to use incremental steps when including new couplings to keep the results as simple as possible. We also chose to limit the number of couplings in the main text for the same reason, i.e., to keep it as simple as possible, and because these couplings have the strongest effect on the model results.

In our simulations, we define the MEW as the range between the two saddle node bifurcations, which can include both stable and unstable branches. In Fig. 3, typical bifurcation diagrams for the AMOC strength (Fig. 3a) and atmospheric pCO₂ (Fig. 3b) versus E_a are shown. Figure 3 specifically shows the configuration where the biological coupling, i.e., where biological export production is dependent on ocean circulation, is used (case BIO). Bifurcation diagrams of the other model configurations discussed here can be seen in Fig. A1 and are very similar to the diagrams shown in Fig. 3.

The bifurcation diagrams show that to be able to simulate the on and off branch, it is vital that the BIO coupling is used. When this coupling is not used, PO₄ concentrations will become negative in the surface ocean under a collapsed AMOC regime. This behavior is illustrated in Fig. A1a and b for case REF. In case REF, the off branch (with negative PO₄) is not shown (Fig. A1a, b), while for case BIO the full bifurcation diagram with two saddle node bifurcations is plotted (Fig. 3). The reason that PO₄ concentrations become negative is that as the AMOC strength declines and less PO₄ is advected into box n, thus decreasing PO₄ concentrations there. As the biological export production is constant in case REF, at some point the sink (i.e., mainly biological export production) becomes larger than the source (i.e., advection of PO₄), and PO₄ concentrations will become negative. This shows that the model without the BIO coupling is unable to capture the carbon cycle of a collapsed AMOC state because of missing processes, most notably the reduction in biological export production under increased nutrient limitation. In Fig. 3b, we can also see the effect of AMOC tipping on atmospheric pCO₂. For the on and the off branch, atmospheric pCO₂ values are relatively constant, and the difference between the branches is approximately 25 to 40 ppm, depending on the case considered, giving values that are of the same order as the values reported in more complex models (Gottschalk et al., 2019). It is good to note here that we do not expect the same response as those found in more complex models, since we employ a steady-state approach, while more complex models use transient simulations that are not yet in equilibrium. However, we would not expect a much larger response in magnitude, and since our response is of a similar order to that in Gottschalk et al. (2019), we have confidence that the model is suitable for our application.

To explain the lower-pCO₂ values on the off branch, we consider the constraint in the model on total carbon content in the ocean–atmosphere system. In the steady state, the total carbon content in the ocean–atmosphere system is not allowed to change. Note that this does not mean that for every E_a value the total carbon content is the same. Different E_a values correspond to a slightly different total carbon content in the ocean–atmosphere system, but for each E_a value, $\frac{\mathrm{dTC}}{\mathrm{d}t}$ is equal to 0. Terrestrial and soil carbon are not considered in this model. This means that the riverine input and sediment outflux of DIC must balance for each value of E_a to keep the total carbon content constant. In our model, the sediment outflux is a function of the CaCO₃ saturation state and CaCO₃ production, which is a function of the rain ratio (constant in non-FCA cases) and the export production. However, in the AMOC off state, the saturation state of CaCO₃ in the ocean is in every box larger than 1, meaning that there is no saturation-driven dissolution of CaCO₃, and the sediment outflux is purely a function of the export production and a constant background dissolution rate. In an AMOC off state, the nutrient advection is relatively low, causing a reduction in export production and therefore a smaller sediment outflux. In the steady state, the riverine influx must balance this small outflux, which is only possible by decreasing atmospheric pCO₂ values.

From the six cases considered here (Table 1), we can see the effect of the individual couplings. As described earlier, the biological coupling is necessary to determine the off branch but does not influence the bifurcation diagrams otherwise. Adding the E_s coupling (E_s as a function of atmospheric pCO₂) alone does not affect the dynamics of the model (Fig. A1c, d) too much since CO₂ concentrations are close to CO_2,0. The rain ratio coupling (FCA; variable rain ratio dependent on CaCO₃ saturation state) decreases atmospheric CO₂ concentrations by 35 ppm and slightly increases the difference in CO₂ concentration between the on and off branch (Fig. A1f). This coupling decreases the atmospheric CO₂ concentrations because, under these settings, the FCA coupling leads to a lower rain ratio compared to a constant rain ratio. As a result, burial of carbon in the sediments is reduced, meaning that the river influx is also reduced, which can only be caused by a lower-atmospheric CO₂ concentration. The climate sensitivity coupling increases this effect by changing the solubility of CO₂ in the surface ocean, with a larger effect for the higher climate sensitivity (Fig. A1h, j). In the cases using the rain ratio, the potential of the E_s coupling becomes visible. In these cases, atmospheric pCO₂ values deviate more from pCO_2,0 and therefore have a larger effect on E_s. When E_s differs from the default value (0.39 Sv), both saddle node bifurcations move to different E_a values.

To explain the movement of the saddle node bifurcations, we consider the sensitivity of the model to E_s (Fig. 4). In Fig. 4, the location of the saddle node bifurcations on both the on and the off branch are shown versus the value of E_s. This figure shows that as E_s increases, the MEW also increases. The default value used for cases REF and BIO for E_s is 0.39 Sv. The CMIP6 CO₂-dependent fit (Eq. 8) results in a slightly smaller value. Due to decreased E_s, the thermocline becomes fresher, and in combination with the salt–advection feedback, this leads to a smaller meridional density gradient and therefore a weaker AMOC. Furthermore, decreased E_s decreases the net evaporation over the Atlantic, given by (E_s-E_a), and this means that a smaller E_a is necessary to tip the AMOC. On the off branch, a smaller E_s results in salinification of the ts box, and a less negative freshwater flux (E_a) is needed to decrease the meridional density gradient and reinvigorate the AMOC. For cases with the FCA feedback, it reduces the MEW by moving the off branch saddle node bifurcation to larger values of E_a and by moving the saddle node bifurcation on the on branch to smaller values, which can be explained by the fact that CO₂ is smaller than CO_2,0, and therefore, E_s is smaller than E_s,base in (Eq. 8).

In the bifurcation diagrams in Figs. 3 and A1, we find that the solution on the on branch becomes unstable before passing the saddle node bifurcation. This change in stability can be explained by the presence of a subcritical Hopf bifurcation in the circulation model. The internal oscillation corresponding to this Hopf bifurcation is unstable and has a multidecadal periodicity. In this study, we are only interested in the MEW of the AMOC, and we therefore do not consider the Hopf bifurcation further.

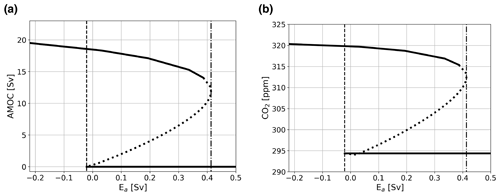
Figure 3 Bifurcation diagram showing the sensitivity of the AMOC and atmospheric pCO₂ to E_a. Solid lines represent stable steady-state solutions, dotted lines represent unstable solutions, vertical dashed–dotted lines represent the location of the saddle node bifurcation on the on branch, and vertical dashed lines show the location of the saddle node bifurcation on the off branch. The case presented here is the one for which biological coupling is used, i.e., case BIO. Bifurcation diagrams of other cases discussed in the main text can be found in Fig. A1.

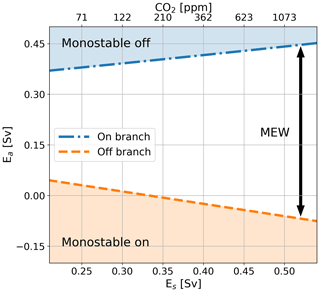
Figure 4 E_a value corresponding to the saddle node bifurcation on the on branch (dashed-dotted blue line) and the off branch (dashed orange line) for different values of E_s in Sv (bottom x axis). The area above the dotted blue line represents the monostable off state, the area below the orange line the monostable on state, and the area in between the MEW. The top x axis represents the CO₂ values corresponding to the E_s values following the fit (Eq. 8); note that this axis is non-linear. The results are based on the dynamical ocean model only where the value for E_s has been changed.

3.3 Sensitivity to total carbon content

Over the Cenozoic, both the AMOC (Lynch-Stieglitz, 2017) and total carbon content in the ocean–atmosphere system have varied (Zeebe et al., 2009; Caves et al., 2016). In Caves et al. (2016), it is suggested that total carbon content has varied between 24 000 and 96 000 PgC. In the previous section, the model was studied with approximately 40 000 PgC in the global system. In this section, we analyze how the sensitivity of the AMOC MEW changes under different total carbon contents in the model. To test the sensitivity, we remove approximately 4000 (−10 %) PgC and add approximately 4000 (+10 %) PgC, 10 000 (+25 %) PgC, and 20 000 (+50 %) PgC. We do this for the cases considered in Sect. 3.2, excluding case REF (Fig. 5).

In case BIO, there is no change in the MEW, which is to be expected since there is no back-coupling from the carbon cycle model to the AMOC model, and the AMOC solution is therefore independent of the carbon cycle. We see only the effect of total carbon content on atmospheric pCO₂ values. When carbon is removed, the CO₂ concentrations at the saddle node bifurcation both decrease. However, when carbon is added, only the saddle node bifurcation on the on branch has higher-CO₂ concentrations, independent of whether 4000, 10 000, or 20 000 PgC is added. We see a similar pattern for the E_s+ BIO case, but here the MEW increases for larger total carbon content due to the different CO₂ concentrations at the saddle node bifurcations. The cases including the rain ratio feedback show a different pattern. Here, the CO₂ concentrations at both saddle node bifurcations are dependent on the amount of carbon added to the ocean–atmosphere system, i.e., the higher the content, the higher the CO₂ concentrations at the saddle node bifurcations (Fig. 5b). This influences the value of E_s at the saddle node bifurcations (Fig. 5c), which increases the MEW for increasing carbon content (Fig. 5a). The MEW shift increases when the climate sensitivity coupling is used (CS_Lo and CS_Hi), with a larger response for the higher sensitivity (CS_HI). Another effect visible in the cases using the FCA feedback is when the difference in CO₂ concentration between the on and the off branch increases as the total carbon content increases. This effect is larger when climate sensitivity is increased.

We can explain the behavior of the MEW in the E_s+ BIO case by looking at the atmospheric pCO₂ values and therefore also at E_s values, the saddle node bifurcations, which are similar for the three high total carbon cases. However, when the rain ratio feedback is used, we see that the MEW keeps increasing for larger carbon contents since the atmospheric pCO₂ also increases. We can explain the difference between E_s+ BIO and the cases where the rain ratio feedback is used by the constraint on total carbon in the ocean–atmosphere system. In E_s+ BIO, biological export production in the Atlantic is mainly a function of the AMOC strength, whereas in the E_s+ BIO + FCA case, it is also dependent on the CaCO₃ saturation state which is coupled to atmospheric pCO₂ through the pH of the surface ocean. This leads to a larger outflux of DIC and Alk to the sediments, which, in steady state, needs to be balanced by a higher influx of DIC and Alk through the riverine flux, which can only be achieved by increasing atmospheric pCO₂.

A second result for the cases with the rain ratio feedback is that the CO₂ concentration difference between the on and off branch increases for a higher total carbon content. As we increase total carbon content in the system, the rain ratio increases on both the on and the off branch because the saturation state of CaCO₃ increases. Due to non-linearities in the carbonate chemistry, the more carbon is present in the system, the larger the difference in the rain ratio between the two branches. This explains why the difference between the on and off branch increases as the total carbon content increases in the system.

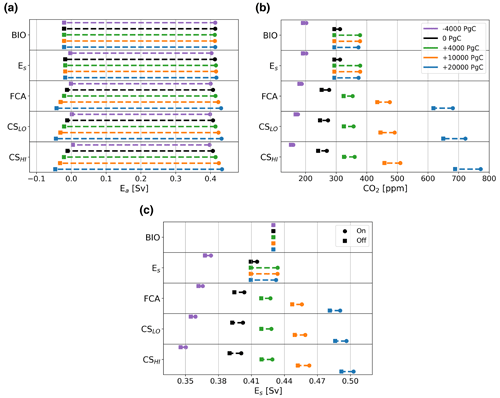
Figure 5 Panel (a) shows the location of the saddle node bifurcations versus E_a (in Sv), panel (b) shows the corresponding CO₂ concentration (in ppm), and (c) shows the corresponding value of E_s (in Sv). The top row of the figure represents case BIO, the second row shows case E_s+ BIO, and the middle row shows case E_s+ BIO + FCA. The fourth row shows case E_s+ BIO + FCA + CS_LO, and the bottom row shows E_s+ BIO + FCA + CS_HI. Square markers represent the location of the saddle node bifurcation on the off branch, and round markers show the location of the saddle node bifurcation on the on branch for cases for which 4000 PgC is removed (purple), the default carbon content (black), 4000 PgC is added (green), 10 000 PgC is added (orange), and 20 000 PgC is added (blue). Note that these values lie well between 24 000 and 96 000 PgC, which is the range of total carbon content throughout the Cenozoic suggested by Caves et al. (2016), and the default total carbon content is approximately 40 000 PgC.

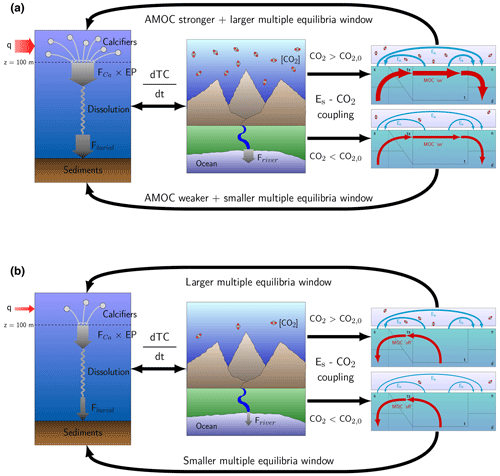
Figure 6 Illustrations of the main mechanisms affecting atmospheric pCO₂ and AMOC stability. Panel (a) shows the mechanisms for the on branch. A strong AMOC increases the export production through an increased nutrient advection (left panel), which is accompanied by high-atmospheric pCO₂ due to the necessary balance between the river influx and sediment burial (middle panel). If the CO₂ concentration is larger (smaller) than CO_2,0, then the AMOC will strengthen (weaken), and the MEW will increase (decrease) (right panels). Panel (b) shows the mechanisms for the off branch. The absence of an AMOC decreases export production through decreased nutrient advection (left panel) accompanied by a low-atmospheric pCO₂ (middle panel). When pCO₂ is larger (smaller) than pCO_2,0 the MEW increases (decreases) (right panel). TC represents total carbon in the ocean–atmosphere system, EP is the export production, and F_Ca is the rain ratio.

4 Summary and discussion

In this paper, we investigated the multiple equilibria window (MEW) of the AMOC in a coupled ocean circulation–carbon cycle box model. When freshwater forcing is coupled to atmospheric pCO₂ using a CMIP6 multi-model fit in Eq. (8) above, the MEW changes slightly due to a dependency on atmospheric pCO₂. We also assessed the sensitivity to the total carbon content in the system and found that the MEW is larger with more carbon in the system due to a shift in both the on and off branch saddle node bifurcations. These results show the potential of the marine carbon cycle to influence the MEW of the AMOC.

The following two processes explain the results on the MEW: (1) the balance between the riverine flux and sediment flux that constrains atmospheric pCO₂ (first two panels in Fig. 6a, b) and (2) the sensitivity of the AMOC to E_s (last panel in Fig. 6a, b). These clear and plausible mechanisms are more important than the precise quantitative estimates and are summarized in Fig. 6. In the model, atmospheric pCO₂ is dependent on the ocean circulation through the effect of export production on the burial of DIC and Alk in the sediments. In the steady state, this burial needs to balance the riverine influx, which is dependent on atmospheric pCO₂. When the E_s coupling is used, E_s is dependent on atmospheric pCO₂, and the ocean circulation is dependent on E_s, creating a feedback loop (Fig. 6). If the CO₂ concentration in the atmosphere is larger than CO_2,0, the MEW increases, while it decreases if it is smaller than CO_2,0. This is the result when E_s is high because atmospheric pCO₂ is high, which results in a stronger AMOC on the on branch. As a consequence, export production is increased, and there will be a larger outflux of carbon and alkalinity through the sediments, which is balanced by a high influx of carbon through the rivers, consistent with high-atmospheric pCO₂ values. Of the feedbacks that we have implemented, only the rain ratio feedback (FCA) affects this mechanism because it directly influences the sediment outflux and makes the carbon cycle less sensitive to the ocean circulation. The E_s–pCO₂ fit used in this study is also important. We acknowledge that it is difficult to assess the validity of the CMIP6 E_s–pCO₂ fit since that fit is based on a transient simulation with a strong forcing. However, longer simulations (i.e., more than 3000 years) by Galbraith and de Lavergne (2019) show a similar, actually slightly stronger, relation to the one used in this study.

What is vital in this mechanism is the riverine flux that is a linear function of atmospheric pCO₂. The linear function we have used in this study is based on the SCP-M (O'Neill et al., 2019), which is based on earlier work by Toggweiler and Russell (2008). In LOSCAR (Zeebe, 2012), a model of similar complexity, the riverine flux is based on a power law. However, this function is defined such that atmospheric pCO₂ converges to a preset value over time, which makes it unsuitable for our study. There are models with more complex weathering terms, including effects of temperature and vegetation, e.g., COPSE (Bergman et al., 2004) and GEOCARBSULF (Royer, 2014), but these are too complex for our model. We could also replace the linear parameterizations with non-linear ones. Powers larger than one will decrease the sensitivity of the model to changes in the burial of CaCO₃ in the ocean, and powers smaller than one will increase the sensitivity of the model. Given that the model does not seem to be very sensitive to non-linear feedbacks in the carbon cycle, we do not expect very different behavior if a non-linear parameterization is used.

The results here can be relevant when studying climate transitions in past and future climates as mechanisms with regard to how AMOC stability can depend on the background climate and atmospheric pCO₂ values identified. Previous work focused on the Pleistocene suggests an influence of atmospheric pCO₂ on the stability structure of the AMOC through temperature (Sun et al., 2022) and moisture transport (Zhang et al., 2017). In our model, there is no direct effect of temperature changes on the AMOC strength, but the E_s coupling used here is similar to the moisture transport described in Zhang et al. (2017). The only difference is that this moisture transport is taken directly to the Pacific basin in their study, whereas in our model, we rescale freshwater fluxes to set this direct flux to zero.

We have used a model that provides a simple framework for studying AMOC dynamics that allows us to efficiently test the concept of AMOC stability in a wide range of parameter values. However, a limitation is that temperature is not a state variable in the model, based on the assumption that the timescales of salinity variations are longer than that of temperature and thus dominantly in a steady state. This means that the AMOC strength in our model is not influenced by changes in temperature, which is a caveat of this study. Under high carbon content in the ocean–atmosphere system, the AMOC does not depend on temperature variations in our model and might not be valid. However, we have explored relatively small changes in the total carbon content, and the mechanisms presented here are also valid for this smaller range, suggesting that the main mechanism presented in this study is at least valid for small changes in the total carbon content. A recent study (van Westen et al., 2024) in which the original box model of Castellana et al. (2019) is extended with dynamical temperature equations shows that under present-day conditions the MEW hardly changes after this extension of the model. Willeit and Ganopolski (2024) show that under higher-CO₂ concentrations, the MEW increases in the Earth System Model of Intermediate Complexity (EMIC) CLIMBER-X. Note that this is done without interactive carbon cycle, so this is just the response of the AMOC to warmer climates in a more complex model than the one used in this study. Based on these two studies, we do not expect that the MEW shift described in this study is fully compensated for when temperature is a state variable.

In van Westen et al. (2024), the original box model was also extended with a parameterization representing the effects of sea ice on the AMOC. This parameterization is based on hysteresis experiments using the Community Earth System Model (van Westen and Dijkstra, 2023). Sea ice insulation effects create a new state in the model with a weak AMOC that extends from the off branch towards lower values of E_a. This effectively increases the MEW in the model, showing that sea ice can play an important role in the ocean dynamics of the model. The weak state is expected to disappear in warmer climates because of the melting of the sea ice. However, the changes in ocean dynamics do not necessarily impact the mechanisms summarized in Fig. 6, and we therefore believe that including sea ice effects would not change the conclusions of our study.

Though not a limitation in the model, it is good to note that the range of timescales in the carbon cycle model is larger than in the circulation model, which does not affect our results but does affect the time-dependent response of the system. As time-dependent effects are not considered, it is difficult to compare our results to existing studies in the literature since these commonly use time integration. Studies using Earth system models on multidecadal to centennial timescales expect that, under climate change, atmospheric pCO₂ values increase following reduced mixing in the North Atlantic (Boot et al., 2023) or a weakening of the AMOC (Boot et al., 2024b; Zhang et al., 2024). On millennial timescales, most studies show an increase in atmospheric pCO₂ after an AMOC weakening (Zickfeld et al., 2008; Gottschalk et al., 2019), but the mechanisms are dependent on the model and the set up of the simulations. The sign of response in the atmospheric pCO₂ in most studies on the multidecadal-to-millennial timescales is at odds with what we found. However, this can be explained in that the final response in our study is mostly dominated by longer timescale processes, i.e., the balance between the weathering and burial of carbon in sediments. Our finding that the MEW increases under higher-CO₂ concentrations is supported by results from CLIMBER-X (Willeit and Ganopolski, 2024). However, as noted earlier, this study does not use an interactive carbon cycle, and the increase in MEW is caused only by the response of the AMOC to a warmer climate.

Our work also holds implications for assessing AMOC stability in future climates. Currently, the global warming threshold for an AMOC collapse is estimated to be 4 °C (Armstrong-McKay et al., 2022). In the future, the carbon content of the ocean–atmosphere system will increase, potentially increasing the MEW, which can change the likelihood of a bifurcation-induced AMOC collapse. In this study, we focused on the slow bifurcation-induced tipping of the AMOC, while the AMOC is also able to tip due to faster processes (e.g., density changes related to temperature variations), resulting in noise-induced tipping (Castellana et al., 2019; Jacques-Dumas et al., 2023; van Westen et al., 2024), and due to rate-induced tipping (Alkhayuon et al., 2019; Lohmann and Ditlevsen, 2021). The mechanisms presented here might influence these noise-induced transitions as well. We hope this work inspires further research on the dependency of the AMOC MEW on the carbon cycle in more detailed models to further investigate the relevance of the mechanism found in this study and provide a better quantification for the influence of the marine carbon cycle on the MEW of the AMOC.

Appendix A: Additional couplings, feedbacks, and simulations

Besides the couplings and feedbacks presented in the main text, we have introduced one additional coupling and two additional feedbacks to the carbon cycle. A summary of these cases and the results can be seen in Table A1 and Fig. A2. The main effects of these additional coupling and feedbacks is a shift in atmospheric pCO₂ values on the on branch for cases with the piston velocity feedback (Eqs. A3 and A4). This shift is larger when also the climate sensitivity feedback is used. A description of the additional coupling and feedbacks is given below.

This coupling increases the concentrations of DIC and Alk in the surface ocean due to evaporation and decreases the concentrations due to a net influx of freshwater at the surface.

$$\begin{array}{}\text{(A1)}& C_{\mathrm{dil},i}={\mathit{\lambda }}_D\times \left(E_{\mathrm{s}}+E_{\mathrm{a}}\right)\times {\displaystyle \frac{C_i}{V_i}},\end{array}$$

where C_i is the tracer concentration in box i, and V_i is the volume. λ_D is a parameter that determines whether the coupling is used (λ_D=1) or not (λ_D=0). The dilutive fluxes for Alk are modeled in a similar fashion.

Table A1 Additional cases not included in the main text using additional feedbacks as described in this document. Results of these cases can be seen in Fig. A2.

A first additional feedback we introduce is a linear temperature dependency in the biological efficiency (Eq. A2), which was introduced in the biological coupling. Under an SST increase, the efficiency will decrease, as follows:

$$\begin{array}{}\text{(A2)}& {\mathit{ϵ}}_i=\left({\mathit{\lambda }}_{\mathit{ϵ}}\times -\mathrm{0.1}\mathrm{\Delta }T\right)+{\mathit{ϵ}}_{i,\mathrm{base}}.\end{array}$$

For this feedback, it is necessary to also use the climate sensitivity feedback, and the strength can be regulated with λ_ϵ.

The second additional feedback allows the piston velocity (k_w) to vary with the SSTs (Eq. A3). When the climate sensitivity feedback is used, this also affects the piston velocity. The temperature dependency is introduced by making the piston velocity a function of the Schmidt number (Eq. A4), as follows:

$$\begin{array}{}\text{(A3)}& \begin{array}{rl}{k}_{w,i}& =\left(\mathrm{1}-{\mathit{\lambda }}_{\mathrm{P}}\right)\times k_{w,i,\mathrm{base}}\\ & +{\mathit{\lambda }}_{\mathrm{P}}{k}_{w,i,\mathrm{base}}\times {\left({\displaystyle \frac{{\mathit{Sc}}_i}{\mathrm{660}}}\right)}^{-\mathrm{0.5}},\end{array}\end{array}$$

where

$$\begin{array}{}\text{(A4)}& \begin{array}{rl}{\mathit{Sc}}_i& =\mathrm{2116.8}-\mathrm{136.25}{T}_i+\mathrm{4.7353}{T}_i^{\mathrm{2}}\\ & -\mathrm{0.092307}{T}_i^{\mathrm{3}}+\mathrm{0.0007555}{T}_i^{\mathrm{4}}.\end{array}\end{array}$$

In this case, the feedback can be either switched on (λ_P=1) or off (λ_P=0). Without this feedback, the piston velocity is similar for all boxes, but with this feedback, the piston velocity will differ per box.

Figure A1 As in Fig. 3 but for the other cases discussed in the main text. (a, b) The case without additional coupling (REF), where the off state cannot be simulated. (c, d) The case with the CMIP6-based E_s and biological coupling (E_s+ BIO). (e, f) The case where the rain ratio feedback is also applied (E_s+ BIO + FCA). Panels (g)–(j) are the same as panels (e) and (f) but also with the climate sensitivity feedback, a low sensitivity (g–h; E_s+ BIO + FCA + CS_LO) and a high sensitivity (i–j; E_s+ BIO + FCA + CS_HI). (a, c, e, g, i) The AMOC strength (in Sv) versus E_a (in Sv), and (b, d, f, h, j) the CO₂ concentration in the atmosphere (in ppm) versus E_a (in Sv).

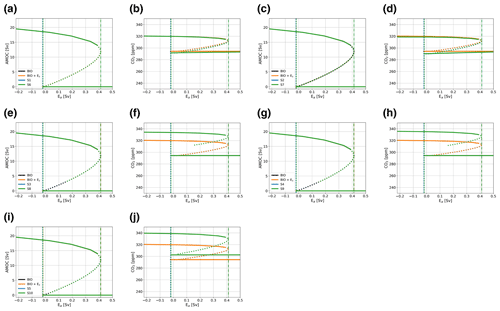
Figure A2 Bifurcation diagrams showing the sensitivity of the model to E_a for additional cases, as defined in Table A1. Solid lines represent stable steady-state solutions, dotted lines represent unstable states, dashed–dotted lines represent the location of the saddle node bifurcation on the on branch, and dashed lines the location of the saddle node bifurcation on the off branch. The black lines represent a case with only the biological coupling (BIO), the orange lines with the logarithmic CMIP6-based E_s and biological coupling (E_s+ BIO), and the blue and green lines represent the cases defined in Table A1. Results are for the AMOC strength (in Sv) (a, c, e, g, i) and atmospheric pCO₂ (in ppm) (b, d, f, h, j).

Appendix B: Model parameters

The model parameters are presented in Tables B1 to B5.

Table B1 Symbol (column 1), description (column 2), value (column 3), and units (column 4) of the general parameters used in the ocean circulation model, based on Cimatoribus et al. (2014).

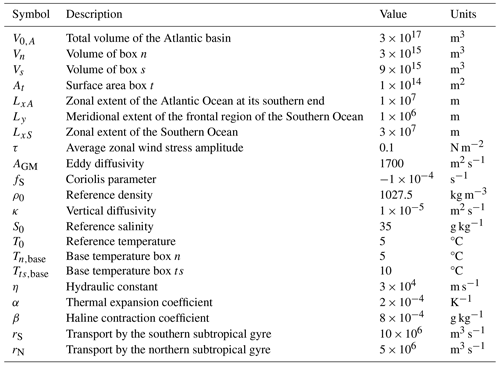
Table B2 Symbol (column 1), description (column 2), value (column 3), and units (column 4) of the general parameters used in the ocean circulation model added or changed with respect to Cimatoribus et al. (2014).

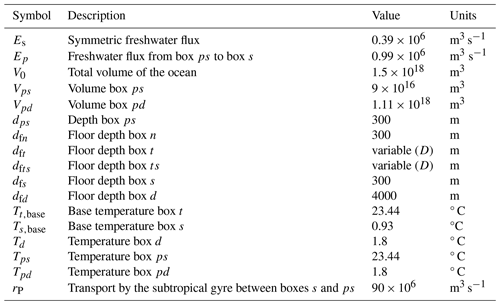
Table B3 Symbol (column 1), description (column 2), value (column 3), and units (column 4) of the general parameters used in the carbon cycle model, based on Boot et al. (2022).

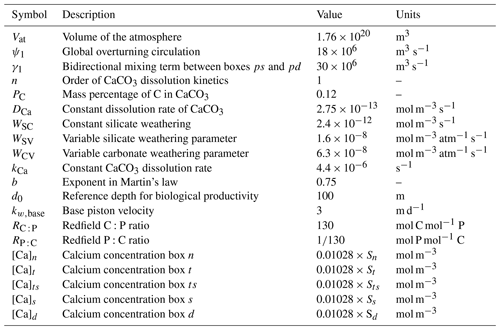
Table B4 Symbol (column 1), description (column 2), value (column 3), and units (column 4) of the parameters used in the carbon cycle model that have been changed compared to Boot et al. (2022).

Weiss (1974)Lueker et al. (2000)Lueker et al. (2000)Mucci (1983)Millero (1983)

Table B5 The symbols and description of the equilibrium constants are presented in the first two columns. The third column presents the source of the used expression.

Appendix C: Model equations

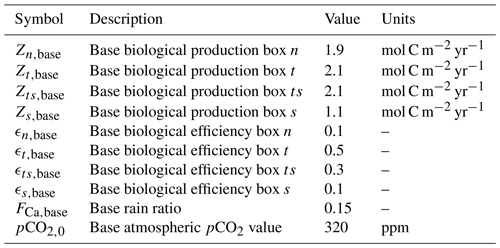
There are 30 state variables in total, namely salinity, DIC, alkalinity, and PO₄ in the seven boxes, the pycnocline depth D, and atmospheric pCO₂. The state variables in the deep-Atlantic box are determined using conservation laws. The salinity equations are given by Eqs. (C1)–(C6), the conservation of salt in the model is given by Eq. (C8), and the pycnocline depth is determined using Eq. (C7). The volume fluxes are determined using Eqs. (C9) to (C13), and the equation of the state is given by Eq. (C14). The equations for the carbon cycle model are given by Eqs. (C15) to (C27).

$$\begin{array}{}\text{(C1)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{d}\left(V_t{S}_t\right)}{\mathrm{d}t}}& =q_{\mathrm{S}}\mathit{\theta }\left(q_{\mathrm{S}}\right)S_{ts}+\mathit{\theta }\left(-q_{\mathrm{S}}\right)S_t+q_{\mathrm{U}}{S}_d\\ & -\mathit{\theta }\left(q_{\mathrm{N}}\right)q_{\mathrm{N}}{S}_t+r_{\mathrm{s}}\left(S_{ts}-S_t\right)\\ & +r_{\mathrm{N}}\left(S_n-S_t\right)+\mathrm{2}{E}_{\mathrm{s}}{S}_{\mathrm{0}},\end{array}\text{(C2)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{d}\left(V_{ts}{S}_{ts}\right)}{\mathrm{d}t}}& =q_{\mathrm{Ek}}{S}_{\mathrm{s}}-q_{\mathrm{e}}{S}_{ts}-q_{\mathrm{S}}(\mathit{\theta }\left(q_{\mathrm{S}}\right)S_{ts}\\ & +\mathit{\theta }\left(-q_{\mathrm{S}}\right)S_t)+r_{\mathrm{S}}\left(S_t-S_{ts}\right),\end{array}\text{(C3)}& {\displaystyle }\begin{array}{rl}{V}_n{\displaystyle \frac{\mathrm{d}{S}_n}{\mathrm{d}t}}& =\mathit{\theta }\left(q_{\mathrm{N}}\right)q_{\mathrm{N}}\left(S_t-S_n\right)+r_{\mathrm{N}}\left(S_t-S_n\right)\\ & -\left(E_{\mathrm{s}}+E_{\mathrm{a}}\right)S_{\mathrm{0}},\end{array}\text{(C4)}& {\displaystyle }\begin{array}{rl}{V}_s{\displaystyle \frac{\mathrm{d}{S}_{\mathrm{s}}}{\mathrm{d}t}}& =q_{\mathrm{S}}\left(\mathit{\theta }\left(q_{\mathrm{S}}\right)S_{\mathrm{d}}+\mathit{\theta }\left(-q_{\mathrm{S}}\right)S_{\mathrm{s}}\right)+q_{\mathrm{e}}{S}_{ts}-q_{\mathrm{Ek}}{S}_{\mathrm{s}}\\ & -\left(E_{\mathrm{p}}+E_{\mathrm{s}}-E_{\mathrm{a}}\right)S_{\mathrm{0}}+\left(r_{\mathrm{P}}+{\mathit{\psi }}_{\mathrm{1}}\right)\left(S_{ps}-S_{\mathrm{s}}\right),\end{array}\text{(C5)}& {\displaystyle }\begin{array}{rl}{V}_{ps}{\displaystyle \frac{\mathrm{d}{S}_{ps}}{\mathrm{d}t}}& =\left({\mathit{\gamma }}_{\mathrm{1}}+{\mathit{\psi }}_{\mathrm{1}}\right)\cdot \left(S_{pd}-S_{ps}\right)\\ & +\left(r_{\mathrm{P}}\cdot \left(S_{\mathrm{s}}-S_{ps}\right)\right)+E_{\mathrm{p}},\end{array}\text{(C6)}& {\displaystyle }{V}_{pd}{\displaystyle \frac{\mathrm{d}{S}_{pd}}{\mathrm{d}t}}={\mathit{\gamma }}_{\mathrm{1}}\cdot \left(S_{ps}-S_{pd}\right)+{\mathit{\psi }}_{\mathrm{1}}\left(S_d-S_{pd}\right),\text{(C7)}& {\displaystyle }\left(A+{\displaystyle \frac{L_{xA}{L}_y}{\mathrm{2}}}\right){\displaystyle \frac{\mathrm{d}D}{\mathrm{d}t}}=q_{\mathrm{U}}+q_{\mathrm{Ek}}-q_{\mathrm{e}}-\mathit{\theta }\left(q_{\mathrm{N}}\right)q_{\mathrm{N}},\text{(C8)}& {\displaystyle }\begin{array}{rl}{S}_{\mathrm{0}}{V}_{\mathrm{0}}& =V_n{S}_n+V_d{S}_d+V_t{S}_t+V_{ts}{S}_{ts}+V_s{S}_s\\ & +V_{ps}{S}_{ps}+V_{pd}+S_{pd},\end{array}\end{array}$$

where θ is a step function which takes a value of one for a positive argument and takes a value of zero for a negative argument. The volume fluxes are given by

$$\begin{array}{}\text{(C9)}& {\displaystyle }{q}_{\mathrm{Ek}}={\displaystyle \frac{\mathit{\tau }{L}_{xS}}{{\mathit{\rho }}_{\mathrm{0}}\left|f_{\mathrm{S}}\right|}},\text{(C10)}& {\displaystyle }{q}_{\mathrm{e}}=A_{\mathrm{GM}}{\displaystyle \frac{L_{xA}}{L_y}}D,\text{(C11)}& {\displaystyle }{q}_{\mathrm{U}}={\displaystyle \frac{\mathit{\kappa }A}{D}},\text{(C12)}& {\displaystyle }{q}_{\mathrm{N}}=\mathit{\eta }{\displaystyle \frac{{\mathit{\rho }}_n-{\mathit{\rho }}_{ts}}{{\mathit{\rho }}_{\mathrm{0}}}}{D}^{\mathrm{2}},\text{(C13)}& {\displaystyle }{q}_{\mathrm{S}}=q_{\mathrm{Ek}}-q_{\mathrm{e}},\text{(C14)}& {\displaystyle }{\mathit{\rho }}_i={\mathit{\rho }}_{\mathrm{0}}\left(\mathrm{1}-\mathit{\alpha }\left(T_i-T_{\mathrm{0}}\right)+\mathit{\beta }\left(S_i-S_{\mathrm{0}}\right)\right),\end{array}$$

where i represents any box.

The carbon cycle equations are given by Eqs. (C15) to C19. The different fluxes are determined using Eqs. (C20) to C27.

$$\begin{array}{}\text{(C15)}& {\displaystyle \frac{\mathrm{d}[\mathrm{DIC}{]}_i}{\mathrm{d}t}}=C_{\mathrm{phys},i}+C_{\mathrm{bio},i}+C_{\mathrm{carb},i}+C_{\mathrm{air},i}+C_{\mathrm{river},t},\text{(C16)}& {\displaystyle \frac{\mathrm{d}[\mathrm{Alk}{]}_i}{\mathrm{d}t}}=A_{\mathrm{phys},i}+A_{\mathrm{carb},i}+A_{\mathrm{river},t},\text{(C17)}& {\displaystyle \frac{\mathrm{d}[{\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}{]}_i}{\mathrm{d}t}}=P_{\mathrm{phys},i}+P_{\mathrm{bio},i}+P_{\mathrm{river},t},\text{(C18)}& {\displaystyle \frac{\mathrm{d}{C}_{\mathrm{tot}}}{\mathrm{d}t}}=C_{\mathrm{river},t}\times V_t+\sum _{i=\mathrm{1}}^{\mathrm{5}}\left(C_{\mathrm{carb},i}{V}_i\right)+\sum _{i=\mathrm{1}}^{\mathrm{5}}\left(C_{\mathrm{bio},i}{V}_i\right),\text{(C19)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{{\mathrm{dAlk}}_{\mathrm{tot}}}{\mathrm{d}t}}& ={\mathrm{Alk}}_{\mathrm{river},t}\times V_t+{\mathrm{Alk}}_{\mathrm{river},ps}\times V_{ps}\\ & +\sum _{i=\mathrm{1}}^{\mathrm{7}}\left({\mathrm{Alk}}_{\mathrm{carb},i}{V}_i\right).\end{array}\end{array}$$

In these equations, the different terms represent advective fluxes (X_phys), biological fluxes (X_bio), carbonate fluxes (X_carb), air–sea gas exchange (C_air), and the river influx (X_river). From these fluxes, C_air only acts on the surface boxes, and X_river only acts on box t and box ps. X_phys is determined as follows:

$$\begin{array}{}\text{(C20)}& X_{\mathrm{phys},i}={\displaystyle \frac{\mathrm{1}}{V_i}}\left(\sum _{i=\mathrm{1}}\left(q_{j\to i}\times X_j\right)-\sum _{i=\mathrm{1}}\left(q_{i\to j}\times X_i\right)\right).\end{array}$$

This equation shows that the concentration of tracer X changes through an advective flux flowing out of box i to box j (q_i→j) times the concentration in box i (X_i) and a flux flowing into box i from box j (q_j→i) times the concentration in box j (X_j). There can be fluxes from multiple boxes into one box.

$$\begin{array}{}\text{(C21)}& C_{\mathrm{air},i}={\displaystyle \frac{K_{\mathrm{0},i}\times k_{w,i}\times {\mathit{\rho }}_{\mathrm{0}}\times \left({\mathrm{CO}}_{\mathrm{2}}^{\mathrm{atm}}-\mathit{\text{p}}{\mathrm{CO}}_{\mathrm{2},i}\right)}{V_i}}\end{array}$$

The value of i is n, t, ts, s, or ps. K₀ is the solubility constant, k_w the piston velocity, CO${}_{\mathrm{2}}^{\mathrm{atm}}$ the atmospheric CO₂ concentration, pCO₂ the partial pressure of CO₂ in the ocean, and V the volume of the ocean box.

$$\begin{array}{}\text{(C22)}& \begin{array}{rl}{C}_{\mathrm{carb},i}& =-{\displaystyle \frac{Z_i\times A_i\times F_{\mathrm{Ca},i}}{V_i}}\\ & +\left({\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]}_i{\left[{\mathrm{Ca}}^{\mathrm{2}+}\right]}_i\right){\mathit{\rho }}_{\mathrm{0}}{k}_{\mathrm{Ca}}\\ & {\left(\mathrm{1}-{\displaystyle \frac{\left({\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]}_i{\left[{\mathrm{Ca}}^{\mathrm{2}+}\right]}_i\right)}{K_{sp,i}}}\right)}^n\\ & \times \mathrm{PerC}+\mathrm{DC}\end{array}\end{array}$$

The value of i is n, t, ts, s, or ps. Z represent biological production, A the surface area of the box, F_Ca the rain ratio, and V the volume. Other variables are the carbonate ion concentration ($\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]$), calcium concentration ([Ca²⁺]), and equilibrium constant for the CaCO₃ dissolution (K_sp).

For box pd, the carbonate flux is determined as follows:

$$\begin{array}{}\text{(C23)}& \begin{array}{rl}{C}_{\mathrm{carb},i}& =\left({\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]}_{pd}{\left[{\mathrm{Ca}}^{\mathrm{2}+}\right]}_{pd}\right){\mathit{\rho }}_{\mathrm{0}}{k}_{\mathrm{Ca}}\\ & {\left(\mathrm{1}-{\displaystyle \frac{\left({\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]}_{pd}{\left[{\mathrm{Ca}}^{\mathrm{2}+}\right]}_{pd}\right)}{K_{sp,pd}}}\right)}^n\\ & \times \mathrm{PerC}+\left({\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]}_{pd}{\left[{\mathrm{Ca}}^{\mathrm{2}+}\right]}_{pd}\right){\mathit{\rho }}_{\mathrm{0}}{k}_{\mathrm{Ca}}\\ & \times {\left(\mathrm{1}-{\displaystyle \frac{\left({\left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]}_{pd}{\left[{\mathrm{Ca}}^{\mathrm{2}+}\right]}_{pd}\right)}{K_{sp,\mathrm{sed}}}}\right)}^n\\ & \times \mathrm{PerC}+\mathrm{DC},\end{array}\end{array}$$

where there is a distinction between water column dissolution of CaCO₃ and dissolution in the sediments.

The biological fluxes in the surface ocean are given by

$$\begin{array}{}\text{(C24)}& C_{\mathrm{bio},i}={\displaystyle \frac{Z_i\times A_i}{V_i}}\times {\left({\displaystyle \frac{d_{\mathrm{fi}}}{d_{\mathrm{0}}}}\right)}^{-b},\end{array}$$

and i is n, t, ts, s, or ps. Z represents biological production, A the surface area of the box, V the volume, and d_fi the floor depth of the box.

The biological flux for box pd is given by

$$\begin{array}{}\text{(C25)}& C_{\mathrm{bio},i}={\displaystyle \frac{Z_{p}s\times A_{p}s}{V_{p}s}}\times \left({\left({\displaystyle \frac{d_{\mathrm{f}ps}}{d_{\mathrm{0}}}}\right)}^{-b}-{\left({\displaystyle \frac{d_{\mathrm{tot}}}{d_{\mathrm{0}}}}\right)}^{-b}\right).\end{array}$$

Alkalinity and phosphate fluxes are proportionate to DIC fluxes as follows:

$$\begin{array}{}\text{(C26)}& {\displaystyle }{A}_{\mathrm{carb},i}=\mathrm{2}\times C_{\mathrm{carb},i},\text{(C27)}& {\displaystyle }{P}_{\mathrm{bio},i}=r_{\mathrm{P}:\mathrm{C}}\times C_{\mathrm{bio},i},\end{array}$$

where r_P : C is a constant stoichiometric P to C parameter.

An explanation and the value of all parameters are given in the tables in Appendix B.

Appendix D: CMIP6 models

Dix et al. (2019)Ziehn et al. (2019)Danabasoglu (2019)Danabasoglu (2020)Scoccimarro et al. (2021)Lovato et al. (2021)Voldoire (2019)Seferian (2018)Swart et al. (2019a)Swart et al. (2019b)E3SM-Project (2022)E3SM-Project (2023)Yu (2019)Li (2019)Song et al. (2020)Guo et al. (2018)Krasting et al. (2018)for Space Studies (NASA/GISS) (2018)for Space Studies (NASA/GISS) (2019)Ridley et al. (2019)Ridley et al. (2020)Boucher et al. (2020)Boucher et al. (2018)Stouffer (2019)Hajima et al. (2019)Tatebe and Watanabe (2018)Neubauer et al. (2019)Wieners et al. (2019)Yukimoto et al. (2019)Cao and Wang (2019)Bethke et al. (2019)Bentsen et al. (2019)Park and Shin (2019)

Table D1 List of CMIP6 models used in this study, with the model name (column 1), member used (column 2), corresponding variable (column 3; either water flux (wfo) or virtual salt flux (vsf)), and reference (column 4).