ESD Ideas: planetary antifragility: a new dimension in the definition of the safe operating space for humanity

Combining well-established non-equilibrium thermodynamic principles and a system dynamics approach, we define, for the first time, the concept of planetary antifragility as changes of Fisher information of Earth's entropy production. As a first approximation for entropy production, we propose using shortwave global albedo anomalies and provide a first quantitative example with data for the July months in the Northern Hemisphere from 1982 to 2010. These preliminary results show a net reduction of 47.63 % in albedo's Fisher information. This loss of antifragility implies a compounding problem because human perturbations such as climate or land-use changes are increasing, but at the same time, the planet is losing its capacity to respond to them. We discuss the concept of antifragility in the context of safe operating space for humanity and planetary boundaries. We conclude that not only does interaction among state variables of the boundaries matter, but more importantly the perturbation response capacity dimension is also missing. In conclusion we speculate on improving the operational definition for ecosystems.

1 Introduction

The planet Earth hosts a complex self-organising system, famously described in the Gaia hypothesis of the physicist James Lovelock and biologist Lynn Margulis in a series of papers in the 1970s (Lovelock, 1972; Margulis and Lovelock, 1974; Lovelock and Margulis, 1974). The system consists of dynamic interactions between both inorganic and organic components that the Gaia hypothesis considered to be self-regulating. Importantly, the organic living component adapts to changing biogeochemical conditions, under thermodynamic constraints, through the process of evolution by natural selection and also changes those conditions as a result of the adaptations (Prigogine et al., 1972; Lovelock, 2016).

Although the Gaia hypothesis has been criticised for being teleological, in other words the system “self-directs” towards conditions best suited to itself, the evolutionary nature of the complex self-organising interactions means that a system without adaptative benefits is not likely to continue (Kirchner, 1989; Baerlocher, 1990). Examples of beneficial interactions are the widespread symbioses of photosynthetic plants with fungi in mycorrhizae and bacteria in nitrogen-fixing nodules for mutual nutrient exchange (Bonfante and Anca, 2009; Bonfante and Genre, 2010). To take this one step further, cell organelles, such as mitochondria and chloroplasts, are considered to be facultative prokaryotic endosymbionts in eukaryotic cells (Martin et al., 2015).

This cellular development and subsequent evolution of the planet's biodiversity has had far-reaching biogeochemical effects. For example, development of vegetation cover changed the composition of the Earth's atmosphere, albedo of the Earth's surface, hydrological cycle and nutrient availability, thereby providing the conditions for further expansion and diversification of life. This complex, dynamic and interacting system continues even if there are substantial external changes, such as the sequence of Croll–Milankovitch orbital cycles considered to be responsible for repeated ice ages and thought to be important drivers of species diversification and range changes, including expansion of modern humans (Bennett, 1990; Lovelock, 1989).

In this sense the Earth's self-organising system, as described by the Gaia hypothesis, can be considered to be “antifragile” in that the response to a potentially catastrophic stressor, even one of the magnitude of shifts in a planet's orbit, leads to continual reorganisation and adaptation that benefits the system as a whole.

Set against this, and related to orbital-driven ice ages, is the rise of the modern human teleological culture that takes actions towards a defined end and that is consequentialist in that the objective of the action is to be achieved by whatever means makes it possible. For example, replacing the Amazon rainforest with grazing land for cattle destined for meat export, or increased agricultural area for commercial livestock feed, is a conscious decision often justified by a need to feed a growing population of humans and bring financial returns where there would otherwise be only forest (Watson, 2004; López-Corona and Magallanes-Guijón, 2020).

The substantial changes made to the Earth in the past few hundred years have led to concern being expressed about a state shifts in the ability of the planet's complex system to respond. In this article we explore the concept of planetary antifragility, following ideas by Michaelian (2015) and Kleidon and Lorenz (2005), as changes of Fisher information of Earth's entropy production using shortwave global albedo anomalies.

Ecosystem antifragility differs from concepts such as resilience and robustness because it contains self-organising and adaptive properties in response to external change. In contrast, a resilient ecosystem is one that can recover from deleterious impacts, and a robust ecosystem is one that is able to resist change. Both resilience and robustness can be incorporated into the concept of antifragility as special cases (Equihua et al., 2020).

In the next section we briefly review the concept of planetary boundaries from an antifragility perspective and present a mathematical definition. We then use satellite measurements of the difference between the incident and outgoing light spectrum of the Earth's albedo as a proxy of planetary-scale entropy production.

Planetary boundaries

The seminal work “Planetary Boundaries: Exploring the Safe Operating Space for Humanity” (Rockström et al., 2009) identified nine core biogeochemical processes with threshold values for each variable called the planetary boundaries (PBs), within which the authors expect that humanity could operate safely. The central idea of their work is that transgressing one or more PBs may lead to a catastrophic planetary tipping point most likely incompatible with modern human organisation survival. Despite the concept of PBs being widely accepted, there are some issues that remain open.

• a.

  As Rockström et al. (2009) recognise, PBs are not interdependent, as transgressing one may both shift the position of other boundaries and cause them to be transgressed, and the true threshold configuration of the individual threshold values of the PBs cannot be established without a metric of the interaction among the whole network of PBs.

• b.

  Rockström et al. (2009) say that the impacts of transgressing PBs will be a function of the social–ecological resilience, but as has been raised recently (Equihua et al., 2020), the concept of resilience is a special and limited case of antifragility.

• c.

  In their work, Rockström et al. (2009) do recognise that although not all processes or subsystems on Earth have well-defined thresholds, human actions that undermine the resilience of such processes or subsystems can increase the risk that thresholds will also be crossed in other processes, such as the climate system.

In that sense the capacity of the Earth system to respond to perturbation under the resilience concept is a key feature in the PB framework. But resilience is a limited special case of the wider concept of antifragility consisting of an intermediate type of response to perturbations near to robustness where the systems tolerate stress and remain the same (Equihua et al., 2020).

As a way of emphasising the importance and rationale of switching from resilience to antifragility, consider that all living systems are undergoing evolutionary processes that require them to do far more than simply endure perturbations. Evolutionary adaptation requires that they must have some features that allow them to not only cope with but gain (up to a point) from perturbations, stressors, variability and uncertainty. This is simple evolutionary and natural selection logic: any system that does gain from variability eventually will outperform its competitors over time. As time is the ultimate source of aleatory, many different types of phenomena can be expressed through time, and an antifragile system will accumulate any gains obtained through aleatory over time. The consequence of this process is that in contemporary populations and ecosystems we see the expression of the accumulation of these advantages over time.

So, through evolutionary processes, what we observe in the present is the predominance of those systems that have previously gained from environmental variability and perturbations. This feature is what Taleb calls antifragility (Danchin et al., 2011; Taleb, 2012) and has a formal definition as a non-linear response in the payoff space and can be summarised as follows (Taleb and Douady, 2013; Taleb, 2018).

Let f(x) be a 2 times continuously differentiable payoff function f(x) with a convexity defined as usual by its second derivative $\frac{{\partial }^{\mathrm{2}}f}{\partial x^{\mathrm{2}}}\ge \mathrm{0}$, which can be simplified without loss of generality as $\frac{\mathrm{1}}{\mathrm{2}}\left[f\right(x+\mathrm{\Delta }x)+f(x-\mathrm{\Delta }x\left)\right]\ge f\left(x\right)$.

From this, we can see that as the dose increases there will be a much higher impact (non-linear) response in f(x), which generalises to a linear combination as $\sum {\mathit{\alpha }}_i=\mathrm{1},\mathrm{0}\le {\mathit{\alpha }}_i\le \mathrm{1}$ in such a way that $\sum \left[{\mathit{\alpha }}_{i}f\right(x_i\left)\right]\ge f[\sum ({\mathit{\alpha }}_i{x}_i\left)\right]$. Then under the correct conditions we may simplify the argument to f(nx)≥nf(x), which implies that the payoff function f(x) of the random variable X with support in [a,b] will satisfy the Jensen inequality and then

$$\begin{array}{}\text{(1)}& \mathbb{E}\left(f\right(x\left)\right)\ge f\left(\mathbb{E}\right(x\left)\right).\end{array}$$

Or as shown in previous work (Taleb and Douady, 2013), the expectation of f under a probability density distribution φ(x) with support in [a,b] indexed by the scale σ is

$$\begin{array}{}\text{(2)}& \forall {\mathit{\sigma }}_{\mathrm{2}}>{\mathit{\sigma }}_{\mathrm{1}},{\mathbb{E}}_{{\mathit{\sigma }}_{\mathrm{2}}}\left[f\right(x\left)\right]\ge {\mathbb{E}}_{{\mathit{\sigma }}_{\mathrm{1}}}\left[f\right(x\left)\right],\end{array}$$

which means that we have either a convex dose-response behaviour over [a,b] or the expectation increases with the scale of the distribution.

Given this precise mathematical definition of antifragility, the problem at hand is to identify a suitable systemic payoff function that adequately captures the idea of planetary antifragility in the context of an enhanced “safe operating space for humanity” that incorporates not only the PBs' state but also the capacity of the Earth to respond in a convex way to the anthropogenic pressures causing the PBs' state to decline.

From previous work on ecosystem antifragility (Equihua et al., 2020) we know that it can be measured using changes in ecosystem complexity, and so the most healthy state should be the one that is at a level of complexity when the ecosystem can self-organise, a state that is reached when ecosystems are in criticality, a dynamic regime characterised by scale invariance in the Fourier space and also in balance between informational emergence and self-organisation (Ramírez-Carrillo et al., 2018). Finally, we also know that in criticality, systems reach their maximum of Fisher information (López-Corona and Padilla, 2019). In this way, antifragility may be approximated using the Fisher information as a payoff time series.

The main idea in this context is that the definition of a safe human operating space should consider not only a “safe” range of important state variables in terms of tipping points, but also the dynamics of the system (see for example unpublished work by Toledo-Roy et al. (2018), https://www.youtube.com/watch?v=WzfdnoC3Kik), especially its capacity to respond to perturbations. The dynamic interpretation of Fisher information could be understood as a measure of the system stability or as we have proposed elsewhere (López-Corona and Padilla, 2019) as a universal payoff function for antifragility.

Also, there is cumulative evidence presented in our previous work on ecosystem antifragility (Equihua et al., 2020) that points to the conjecture that the Earth system should not only be under a limited range for key biogeochemical variables but also in a criticality regime (Hidalgo et al., 2014) in which the system is at its maximum complexity, maximum Fisher information and balance between emergence (flexibility/randomness) and self-organisation. Under these conditions, ecosystems (including Earth systems) exhibit the greatest computational and inferential capacities related to the system capacity to respond and adapt to perturbations.

Figure 1 July shortwave terrestrial albedo time series from GLASS data for the Northern Hemisphere.

2 Methods

2.1 Entropy production as a payoff function

Albedo anomalies as antifragility estimates

As noticed in previous work by Michaelian (2005, 2015), ecosystems arise and evolve, as any other physical system, under the laws of thermodynamics. In particular, the relation between entropy production and ecosystem functioning up to the Earth system is well established and has been studied since 1972 in the pioneering work of Prigogine et al. (1972) and then by Ulanowicz and Hannon (1987), Aoki (1989), Schneider and Kay (1994), Schymanski et al. (2010), Michaelian (2005, 2012, 2015), Kleidon and Lorenz (2005), Kleidon (2009, 2010a, b, 2021), Kleidon et al. (2010), and Panwar et al. (2020).

In the current paper, we build our new planetary antifragility concept mainly on the work of Michaelian (2015), who proposes that healthy ecosystems have a bigger entropy production than unhealthy or stressed ones, and entropy production should then be a reliable indicator of their health, given by the following expression of total entropy production (more precisely photon dissipation) per unit area of the ecosystem (J) (Michaelian, 2015):

$$\begin{array}{}\text{(3)}& \text{health}=J=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\mathrm{2}\mathit{\pi }{L}_{\text{rad}}\left(\mathit{\lambda }\right)-\mathrm{0.04}{L}_{\text{in}}\left(\mathit{\lambda }\right)\mathrm{d}\mathit{\lambda },\end{array}$$

in which the 2π comes from a solid angle calculation assuming isotropic emission and predominantly Lambertian reflection as a consequence of leaves diffuse scattering and the collective effect of multiple leaves in the ecosystem (Gates, 2012). The 0.04 factor comes from the cosine of the angle of the incident radiation, and both entropy fluxes [$\mathrm{J}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$], L_rad(λ) and L_in(λ) come from the following expression as a function of energy flux I(λ) [$\mathrm{J}{\mathrm{m}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$]. In the case of L_rad(λ), we have I=I_rad measured by a detecting spectrometer, and for L_in(λ) the I=I_in measured by solar spectrum at surface.

$$\begin{array}{}\text{(4)}& \begin{array}{rl}L\left(\mathit{\lambda }\right)=& {\displaystyle \frac{n_{\mathrm{0}}kc}{{\mathit{\lambda }}^{\mathrm{4}}}}\left[\left(\mathrm{1}+{\displaystyle \frac{{\mathit{\lambda }}^{\mathrm{5}}I\left(\mathit{\lambda }\right)}{n_{\mathrm{0}}h{c}^{\mathrm{2}}}}\right)\ln \left(\mathrm{1}+{\displaystyle \frac{{\mathit{\lambda }}^{\mathrm{5}}I\left(\mathit{\lambda }\right)}{n_{\mathrm{0}}h{c}^{\mathrm{2}}}}\right)\right.\\ & \left.-\left({\displaystyle \frac{{\mathit{\lambda }}^{\mathrm{5}}I\left(\mathit{\lambda }\right)}{n_{\mathrm{0}}h{c}^{\mathrm{2}}}}\right)\ln \left({\displaystyle \frac{{\mathit{\lambda }}^{\mathrm{5}}I\left(\mathit{\lambda }\right)}{n_{\mathrm{0}}h{c}^{\mathrm{2}}}}\right)\right],\end{array}\end{array}$$

where λ is the wavelength of energy flux I(λ) [$\mathrm{J}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$], c is the velocity of light, n₀ is the photon's polarisation sate (n₀=1 for polarised and n₀=2 for unpolarised), and h and k are as usual the Planck and Boltzmann constants.

The key point here is that we do not need to account for all individual living systems that have several non-linear couplings among both biotic and abiotic (i.e. water cycle) components of the Earth system but can use a global planetary “good enough” approximation of the entropy production (more precisely photon dissipation) contribution by the biosphere. Nevertheless, it is necessary to find a specific proxy that contains the most relevant information on the entropy production of ecosystems that is measured at a planetary scale and available from existing databases. So, following original ideas discussed by Ulanowicz and Hannon (1987) and Michaelian (2015), we propose that this proxy can be represented by the difference between the incident and outgoing light spectrum based on satellite measurements of albedo as in Eq. (3).

In this work, we used published data for surface albedo anomalies of the Northern Hemisphere during the months of July (GLASS albedo product) for 1981–2010 (He et al., 2014) and calculated its Fisher information in the same way Ahmad et al. (2016a) have done for global mean temperature (1880–2015). In their work, the authors organised the time series data such that each month represents one system variable so that 12 variables describe global temperature anomalies from January to December for each time step (year).

Figure 2 Fisher information for July shortwave terrestrial albedo time series from GLASS data for the Northern Hemisphere.

2.2 Data inputs

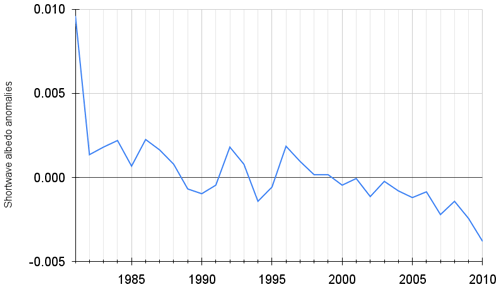
Data used here (Fig. 1) come from the Global Land Surface Satellites (GLASS), which uses very high-resolution radiometers (AVHRR) and MODIS (Moderate Resolution Imaging Spectroradiometer) data (Liang et al., 2013). Two direct albedo calculations are incorporated for the MODIS component: one for surface reflectance and one for top-of-atmosphere (TOA) reflectance (Qu et al., 2007). The AVHRR observation GLASS albedo component is based on a direct measurement algorithm using radiometric calibration and atmospheric correction surface reflectance (Pedelty et al., 2007) comparable to that used on MODIS data (Liu et al., 2013).

We used the 1982 to 2010 time series of July months for the Northern Hemisphere (more land area implies more albedo changes and higher rates of climate change are expected), which show a decrease rate of 0.0013 per decade (p < 0.01) (Fig. 1) (He et al., 2014). We took this data set because it is the season when less snow or ice may be found in the Northern Hemisphere, and so a clearer response by the vegetation to climate change could be found. We then used a Python implementation of the algorithm created by Ahmad et al. (2016a) to assess Fisher information, available at https://github.com/csunlab/fisher-information (last access: 22 July 2022).

In this work, we are only using land albedo, as the original input does not include ocean surface albedo. The different albedo products derived from satellite imagery, in general, are processed only for terrestrial surfaces because ocean albedo is rather stable and low, which may cause higher fluctuations to get masked/averaged by ocean albedo. So, the influence of periodic phenomena like El Niño–Southern Oscillation (ENSO) could not affect the results because of the change in ocean surface albedo. But it must be considered that land cover, which influences terrestrial albedo to a large extent, is heavily influenced by the teleconnections caused by “spatially and temporally large-scale anomalies that influence the variability of the atmospheric circulation” (ENSO, Arctic Oscillation, North Atlantic Oscillation, Pacific Decadal Oscillation, Pacific North America Index; https://www.ncdc.noaa.gov/teleconnections/, last access: 28 July 2022). This leads to climate anomalies linked across geographically separated regions and also to bigger or smaller changes in land cover type (e.g. arid environments with abrupt growth of annual plants after unusual precipitation or drought-related phenotypical changes in normally humid areas). For further work after this proof of concept, it will be interesting to compare the dynamics of both hemispheres.

2.3 Stability analysis using Fisher information

Consider a dynamical system characterised by a phase space $s=(x_{\mathrm{1}},\mathrm{\dots },x_i,\mathrm{\dots },x_m)$ built up n state variables x_i under which a measurement y is made; then we can define the quality of the measurement by its Fisher information:

$$\begin{array}{}\text{(5)}& I\left(s\right)={\displaystyle \frac{\mathrm{1}}{T}}\underset{\mathrm{0}}{\overset{T}{\int }}{\displaystyle \frac{s^{\prime \prime \mathrm{2}}}{s^{\prime \mathrm{4}}}}\mathrm{d}t,\end{array}$$

where T is the time period required for the system to complete a cycle, and s^′(t) and s^′′(t) are the tangential velocity and acceleration of the system in the phase space, calculated as a function of the state variables x_i given by

$$\begin{array}{}\text{(6)}& {\displaystyle }& {\displaystyle }{s}^{\prime }\left(t\right)=\sqrt{\sum _i^m{\left({\displaystyle \frac{\mathrm{d}{x}_i}{\mathrm{d}t}}\right)}^{\mathrm{2}}},\text{(7)}& {\displaystyle }& {\displaystyle }{s}^{\prime \prime }\left(t\right)={\displaystyle \frac{\mathrm{1}}{s^{\prime }\left(t\right)}}\sum _i^m\left({\displaystyle \frac{\mathrm{d}{x}_i}{\mathrm{d}t}}{\displaystyle \frac{{\mathrm{d}}^{\mathrm{2}}{x}_i}{\mathrm{d}{t}^{\mathrm{2}}}}\right).\end{array}$$

This dynamic interpretation of Fisher information (Frieden, 2007; Fath and Cabezas, 2004) implies that if the system is a constraint to small tangential velocities and acceleration, then in a specific measurement time range the system will occupy a small hyper-volume, which is interpreted as the system being stable.

In this way, dynamic stability corresponds with higher levels of constant Fisher information. It then follows that self-organised systems would tend to reduce their variability by gaining Fisher information. On the other hand, a loss of stability would be indicated by a reduction in the system's Fisher information, and sudden sharp changes could be used as an early warning of tipping points.

3 Results

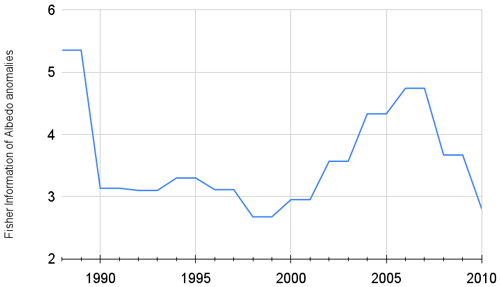
In Fig. 2 we show the Fisher information for 1988–2010 (the algorithm requires an initial calculation using the first 7 data points) of Northern Hemisphere albedo, which exhibits an oscillation with a mean value of 3.59, a maximum value of 5.35 in 1988, a minimum of 2.55 in 1998 and a net reduction of 47.63 % between 1988 and 2010. The reduction does not occur linearly but shows an oscillating behaviour: a first decrease happened between 1988 and 1998, followed by a gradual increase until 2007 to again decrease until 2010.

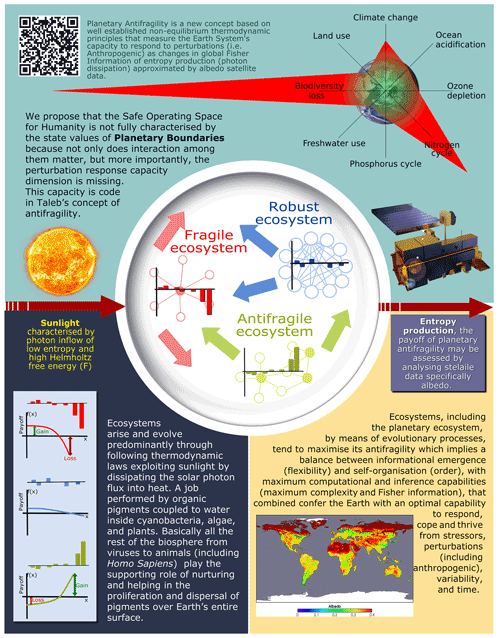
Figure 3 Original figure for the article. Planetary antifragility is a new concept based on well-established non-equilibrium thermodynamic principles that measure the Earth system's capacity to respond to perturbations (i.e. anthropogenic) as changes in global Fisher information of entropy production (photon dissipation) approximated by albedo satellite data.

These results are not meant to provide a complete data analysis on planetary antifragility using Fisher information of land albedo (for example, consider the oceanic and hemispheric contributions already discussed). In this paper we are presenting a preliminary analysis to demonstrate that it is possible to evaluate planetary antifragility in a scientifically sound way (Fig. 3) and more importantly to point the way to further future development of this original idea.

It is important to note that an ESD Ideas article type such as the present one “presents innovative and well-founded scientific ideas in a concise way that have not been comprehensively explored”, and the main result of the article is the planetary antifragility idea itself (Fig. 3). This idea opens several paths: (1) a way to use a unified co-evolutionary representation for coupled human and natural systems (CHANS); (2) introduce a precise and quantifiable mathematical framework to systematise the interdisciplinary nature of CHANS; (3) promote and enhance the understanding of the dynamics of emerging, transitional and extreme regimes; (4) increase the interest in developing artificial intelligence tools (including machine or deep learning) for interdisciplinary analysis beyond a mechanistic paradigm; and (5) the potential to incorporate mathematical methods to improve decision-making processes, incorporating CHANS risks aspects.

4 Discussion

The safe operating space for humanity is not fully characterised by the state values of planetary boundaries because not only does interaction among them matter, but more importantly the perturbation response capacity dimension is missing.

As pointed out in a recent work (Hillebrand et al., 2020), a key dimension of understanding ecosystem responses to anthropogenic global change is to test if the ecosystem really goes through thresholds or tipping points. In their work, the authors found that threshold transgressions were rarely detectable, either within or across meta-analyses.

As also commented on by Dudney and Suding (2020), and as we have been highlighting in this work, ecosystems seldom respond to environmental drivers in isolation, and the inclusion of interacting drivers may indicate more frequent threshold dynamics than expected from meta-analyses (Hillebrand et al., 2020). In this way, our thermodynamic framework using global albedo as a proxy of planetary entropy production could be interpreted as a systemic response that integrates all drives and responses.

The informational approach using Fisher information as a measure of the entropy production stability leads to the notion of homeostasis, which has been re-framed in terms of time series analysis in a medical application (Fossion et al., 2018). In their work, they found that when the human body needs to maintain some homeostatic physiological process (keep it within a defined range of values) such as blood pressure this is achieved by coupling it with another process that absorbs variability from the environment. For homeostasis of blood pressure, the heart rate needs to absorb environmental volatility. They show that healthy people have a blood pressure that is normally distributed, while heart rate is skewed to the right. Whereas when there is a chronic disease such as diabetes, blood pressure is no longer Gaussian and generates a skew to the left, while heart rate becomes normally distributed. When a process is normally distributed, it means that there is a well-defined characteristic scale around which all values are clustered, with very few extreme values. Conversely, having skewed distributions means that there are many extreme events, which in fact dominate the phenomenon to the degree that the characteristic scale can be lost.

Homeostatic processes could explain why threshold transgressions were rarely detectable in ecosystems that are self-organising to prevent tipping point events. For example, we could consider ecosystem functions as homeostatic processes maintained by the fluctuations in species composition. In this case, compositional shifts should be much more prone to threshold dynamics than ecosystem functions.

Also interesting is the similarity between the results of Fossion et al. (2018) and Taleb's ideas about antifragility (Taleb, 2012). This made us recontextualise ecosystem homeostasis or resilience, as it is generally identified in ecology, as a particular case of Taleb's conceptual framework, in which a system can be fragile, robust or antifragile, depending on how it responds to disturbances in its environment (see Fig. 1). As quantitative antifragility is measured as the system's response to perturbation, in order to evaluate it one needs to identify the adequate payoff function; in this case, we argue that planetary entropy production can be approximated by Earth's albedo.

Using published data (He et al., 2014) we calculated Fisher information for 1988–2010 of Northern Hemisphere albedo, which exhibits an oscillation with a mean value of 3.59, a maximum value of 5.35, a minimum of 2.55 and a net reduction of 47.63 %, with a rate of 0.0013 per decade (p < 0.01) that is in agreement with findings by Marcianesi et al. (2020), who calculated, for example, a global clear-sky albedo (%) decrease of 0.24 % per decade, with the confidence of 99 % for land, and a decrease of 0.66 % per decade, with the confidence of 99 % for land. In this context land-use changes might be an important driver for antifragility loss.

Observed oscillation in Fisher information values could be interpreted as a cyclical decrease in Fisher information, as the increase after the completion of one cycle does not rebound to the original value but stays below. This decrease would be associated with a loss of stability (degradation?) overlapped with oscillations caused by changes in terrestrial albedo as a response to teleconnected climate oscillations.

Another interpretation related to this cyclical pattern could be based on critical slowing down: Strogatz (1994) proposed critical slowing down as representing the major contribution from the authors. Critical slowing down “implies that recovery upon small perturbations becomes slower as a system approaches a tipping point” (Scheffer et al., 2015). This could explain why the recovery after the first cycle of loss of Fisher information does not reach the original value, as a slowing down means less recovery in the same amount of time. If the time of recovery and loss of Fisher information is determined by oscillating climate phenomena, a slowing down of recovery would mean less recovery between cycles.

But considering the overall Fisher information lost, it is not only that the planet is decreasing its albedo as a response to human perturbations (mainly climate change and land use change) as the data show: if albedo is a proxy of entropy production, what Michaelian recognised as the thermodynamic function of life (Michaelian, 2012), then loss of albedo's stability means the planet is losing a key feature of its dynamics: in other words, its antifragility.

This means that we may have a compounding problem because human perturbation such as climate change is increasing, but at the same time the planet is losing its capacity to respond to it. In that sense, we need to not only reduce or capture CO₂ emissions, but we should also restore Earth's antifragility, which means restoring its ecosystems.

Now let us consider some problems or limitations.

1. In human health assessment the first-order approximation has been identified with the previously known reference range of value of some key physiological variables such as heart rate and systolic blood pressure. So one problem with using visible albedo as a proxy for global entropy production is we do not have the equivalent of those reference values, which in this case should be determined for each ecosystem type. In that sense, visible albedo should be applied in a spatially explicit way, not averaging mean values over large regions, but using local values because the values need to be evaluated against the correct reference values.

2. Another problem would be considering visible albedo values without their dynamics, as can be illustrated with an analogy to human health: consider a person with a broken arm (unhealthy state) but a healthy heart (healthy dynamics) versus an Olympic athlete (healthy state) but with a condition prone to sudden cardiac syndrome (unhealthy dynamics). Given these two considerations, we decided not to rely on the direct value of albedo but rather its Fisher information, which encodes the system's dynamics in terms of its capacity to respond to perturbations.

3. As suggested by Michaelian (2015), other problems could be that the real extent of the ecosystem considered in the measurement depends on the height of the remote sensor because of the relation with the solid angle of the detector.

4. Consider that an albedo value is an “instant” measurement and it could be necessary to integrate measurements across a 24 h cycle (if possible) or other longer cycles, but perhaps this is not important for a long-term analysis, as presented in this work. Nevertheless, it does point to the fact that this work does not present a fully developed framework for planetary antifragility. We still need to resolve whether remote sensing measurements of albedo really can sufficiently capture entropy production, or if other signals would be needed. This would most likely be the case when working at a more detailed scale, for example, on a particular ecosystem in a defined region.

This brief concept paper is a first illustration of the general idea of using antifragility as a new dimension in the definition of the safe operating space for humanity. As a follow-on from discussing some aspects of the advantages and problems with using albedo measurements derived from satellite imagery in this paper, we would very much like to further explore other variables that could be used to construct indicators for planetary antifragility.

In addition to albedo, we think it would be very interesting to eventually incorporate other measurable proxies for entropy production sources, such as the bioacoustic signals and perhaps also ecosystem respiration. Every sound emitted by a living agent in an ecosystem is coding a part of the ecosystem metabolism into the signal. Important bioacoustic signals are produced by members of the animal kingdom and would prevent the problem posed by defaunated ecosystems, which from a vegetation perspective using measures such as albedo could give a signal of being healthy (at least in the short term). Ecosystem respiration is a good proxy because it includes soil respiration, and soil is a complex system that incorporates all spheres (biosphere, geosphere, atmosphere, hydrosphere), several biogeochemical processes, and many spatial and timescales, so it links many sources of information about the ecosystem in a single measure. Although there are major projects such as AmeriFlux (https://ameriflux.lbl.gov/, last access: 22 July 2022) that collect data of ecosystem respiration (among others) in many places of North America, currently there are not enough data available for considering these variables at a planetary scale. However the concept may downscale to ecosystem scale using both remote sensing and in situ data, which could work also as a benchmark against other ecosystem health metrics such as integrity.

Finally, as always happens when introducing a new concepts, the revised perspective leads us to revisit others: in this case, the ecosystem definition that traditionally is understood in its basic form as a spatially explicit community of living organisms in conjunction with the nonliving components of their environment, and which interacts as a system. As pointed out by Jax (2007), managing ecosystems or increasing their theoretical understanding requires a clear conceptualisation of what ecosystems are (Schaeffer and Cox, 1992; Sagoff, 2003; Jax, 2005); however, there are different and sometimes incompatible definitions of the notion of ecosystem (see e.g. Jax et al., 1998; Jax, 2006).

Depending on the specific definition in use, there might be different sets of questions that are difficult to answer. In particular, under the basic definition given above, how many different species and interactions are necessary to constitute an ecosystem? Is a community of trees of different species an ecosystem? What about function, dynamics and stability? Are there any requirements in terms of spatial extension and connectivity? Are there different types of ecosystems; for example, what happens with modified, degraded or perturbed “ecosystems”? To what extent is a “modified” ecosystem of type A still an A ecosystem? Based on what characteristics should a type of ecosystem should be defined? What happens with different ecosystems that share some interactions or species? Does this definition allow us to understand predicted succession and ecological tipping points?

Also, as commented on by Sagoff (2003), to improve our understanding about ecosystems, including the planetary ecosystem, its definition should

1. define and classify them, and thus determine the conditions under which it remains the “same” system through time and change;

2. find ways to reject as well as to create mathematical models of the ecosystem functioning and evolution;

3. make it possible to identify efficiently the causes of ecosystem organisation;

4. show how ecology can potentially help to solve socio-environmental problems.

We think that the antifragility framework could help to improve ecosystem definition in a manner that makes many of these questions and goals are easier to tackle. So we are incorporating the ideas of this paper in this new definition: an ecosystem is an open thermodynamic system constituted by a community of living organisms in conjunction with the nonliving components of their environment that through its interactions and evolutionary processes, constrained by the external conditions, self-organised in a maximum solar photon flux dissipation, in which the system is at criticality, with maximum computational and inferential capabilities that allow it to respond and thrive under uncertainty, stressors, perturbations and ultimately time, in a well-defined geographic context.